电子探针微量元素分析的一些思考

李小犁

北京大学 造山带与地壳演化教育部重点实验室，北京 100871

电子探针显微分析（EPMA, Electron Probe Micro Analysis/Analyzer）是分析化学中的一种常见仪器分析方法（以下简称电子探针），其最大的优点在于，能够原位（in-situ）地对样品的某个微小区域（～1 μm）进行定性和定量分析，并且不会导致明显的物理化学损坏（伤）。世界上第一台电子探针是由法国人Castaing于1951年设计制造（Castaing and Guinier, 1949; Castaing, 1951），这是电子光学技术与X射线光谱分析技术交叉融合的必然产物（Moseley, 1913; Siegbahn, 1931）。电子探针利用的是一束可聚焦到无穷细小的高能量加速电子（5～30 kV），来对试样微区进行轰击，从而激发出不同的X射线能量（光子），然后经过探测系统（分光晶体和检测器）的捕捉以及后期计算机软件分析处理，将其转换为相应的元素类型和含量信息。与此同时，在电子轰击下，也伴随有其他能量的释放（背散射电子、二次电子、透射电子、吸收电子、阴极发光等），可以提供相应的电子图像信息。电子探针分析可以在非常高的空间分辨率（二次电子图像，10 nm）条件下，同时获取微区的形貌和成分图像信息，并且不破坏样品的原结构，其所能完成的分析测试工作是其它分析化学仪器不可替代的。理论上，电子探针可以分析从4号元素铍（Be）到92号元素铀（U）之间的所有元素，几乎包含了目前已知的绝大多数元素，是现代科技发展的重要技术支撑，在物理、化学、化工、地质、材料、冶金、机械、环境、以及微电子、生物医学等领域都有广泛应用（徐萃章，1990）。电子探针分析一般利用的是元素内层电子所激发的X射线，因此其分析结果不受元素的化合价态影响。

电子探针定性分析的物理基础是Moseley定律，即：组成物质（化合物/单质）的元素（原子序数Z）与它在激发态发生的特征X射线（波长λ）之间存在着单值关系，每一个元素都有一个和/或一组特定的特征X射线与之对应，并且其不随轰击电子能量（强度）的变化而改变。电子探针分析的原理就是通过测量某个特征X射线的波长，即X光量子能量，来获知测试样品中的元素信息。而电子探针定量分析的物理基础是对比分析原理，须引入标准物质进行标定：试样中的元素A的相对含量CA与该元素的特征X射线的强度IA（即计数）具有正相关关系，含量C越高，其X射线强度越大；在同样的实验条件下，通过测量已知样品标准物质和未知待测样品中的A元素的同一个特征X射线谱线（例如Kα谱线），经过对比校正计算，即可得到元素A在未知样品中的相对含量CA。这里的标准物质是科学制定和有效实施的技术标准，控制和保证了分析测试资料的可靠性、准确性，并提高了产品质量的实物标准；而标准物质又与标准技术密不可分，标准物质的研制需要以技术标准为依据和基础。

电子探针定量分析以及其他类型的微束成分分析，归根结底都是对比分析，其分析的准确度在很大程度上取决于标准物质的稳定性和可靠性。在电子探针微量元素（定性和定量）分析中，除了选择合适的标准物质，还需要对仪器参数进行适当调整，合理设置适宜的实验条件（Fialin et al.,1999），并且在数据（预）处理上进行仔细甄别以及合法性研判。对于复杂的地质类天然岩石样品，微量元素的赋存大都具有标型意义，在探讨某些重要的科学问题中具有非常关键的指示意义。例如，在岩石学中广泛应用的副矿物中微量元素温度计，包括金红石的Zr温度计（Zack et al., 2004;Tomkins et al., 2007）、锆石的Ti温度计（Watson et al., 2006; Ferry and Watson, 2007）、石英的 Ti温度计（Wark and Watson, 2006; Thomas et al., 2010）等等。而在经济矿产学中，电子探针通常作为首选的便捷高效低成本的测试方法应用于（硫化物）矿床（矿石）中的贵金属（Au、Ag、PGE等）的含量分析，并对探讨如Au在黄铁矿中的赋存态（Shao et al., 2018）以及其成因机制（Reich et al., 2005）具有重要意义，并可为矿石品位信息提供重要参考。同时，对于稀土元素（磷灰石、独居石、榍石等）（Lloyd et al., 1996; Jercinovic, 2008; Goemann, 2011;Lowers et al., 2017）以及相关的Th-Pb-U化学定年CHIME方法（Suzuki and Adachi, 1991a, b; French et al., 2002；张文兰等，2003），和F、Cl卤族元素（磷灰石）（Li and Hermann, 2015），超轻元素Be（张文兰等，2006，2020；吴润秋等，2020）和B（Meier et al., 2011; Cheng et al., 2019）在相关矿物中的测试，乃至对变价元素（如Fe3+）在某些氧化物类型矿物中的定量分析（Höfer et al., 1994, 2007,Enders et al., 2000）等等，都是目前电子探针分析技术中的难点（张迪等，2019；陈意等，2020）。微量元素的电子探针分析大都要求特殊的仪器参数设置和专门的实验条件建立，以及数据结果的（预）处理和后期校正计算等人工介入，要求测试者不但具备专业的分析技术知识，并且能够正确理解实验测试所需解决的科学问题。在此，本文将以日本电子（JEOL）公司的电子探针JXA系列为例（JXA 8100 & 8230），对电子探针微量元素定量分析中需要注意的几点关键内容进行概要讨论。

1 分析实验条件

在电子探针微量元素分析中，首先必须根据具体的试样类型（氧化物、碳酸盐、硫化物等）来单独设定各自独立的实验条件。因此，定量分析的前提必要条件是进行定性分析，即确定待测样品的种类。通常来讲，为了使试样中的微量元素能够激发出足够多的特征X射线信号——清晰明辨的谱线位置和足够多的强度计数量，一般可以采用增加激发能量（加速电压、轰击束流）和、或延长谱仪采集时间的途径。但是这时候大都会面临主量元素干扰问题：主量元素的含量是相对较高的，那么在高能量或长时间轰击下更会激发出更高的强度计数，极易超出计数器所能够收集的信号强度范围，出现死时间（Dead Time）状态，导致分析结果的不准确。为避免此类情况的发生，应该把测试方法分为两步进行：（1）单独的主量元素分析测试，忽略微量元素的测量，并同时进行多点分析测试平均含量的方法保证主量元素分析的可靠性；（2）利用探针分析软件中的CAL功能（如JEOL系列电子探针），把上述步骤所测得的主量元素（平均）含量输入到分析条件中，设为固定值，不进行测量。然后再设置较高的轰击电流和、或延长采集时间来分析微量元素。该方法可以有效保证主量和微量元素都能够被准确分析，避免测试中因某个/些元素的特征X射线的信号过强（高计数）或过弱（低计数）导致测试不准确。但是，必须注意的是，加大电流、延长计数时间的前提必要条件是：被测样品本身在该实验条件下能够保持物理化学稳定，并不含有易挥发、逃逸的气相元素（F、Cl、S、C等）以及化学活性高的元素（如碱性金属）。

在微量元素电子探针分析的实验条件设置中，除了简单的加大电流、延长驻留测试时间来测试微量元素，还应该注意一下至少四个方面的内容：（1）波谱仪测试晶体的合理选择；（2）元素谱线重叠峰、干扰峰的识别区分和背景值的设定；（3）脉冲幅度分析器（PHA）的设定；以及（4）标准物质的合理选择与标定。

1.1 波谱仪测试晶体的合理选择

通常来讲，不同分光晶体可测量元素的范围是可以小范围重合的，即某些元素可以被几种类型的分光晶体测量。例如，Ti元素既可以用PET晶体，也可以用LIF晶体进行测定。这时候就涉及到如何选择晶体的问题。不同的分光晶体对元素的辨析能力是有差别的，同样以Ti元素为例，在PET晶体中的其衍射角度低，因此具有较小的Kα谱线峰位L值，且峰形较宽，具有很高的强度计数（10 000个单位）；但是，在LIF晶体中，其衍射角度较高，具有较大的Kα谱线峰位L值，且谱峰形状尖锐，但是强度计数却很低（600个单位）（图1）。这个时候，在实际测试分析工作中，采用哪一个晶体（谱仪）来测量Ti元素更适宜就需要作出合理判断。

1.2 元素特征谱线的重叠峰处理和背景值设定

在电子探针分析中，需要首先考虑到的重要问题就是元素特征峰位的重叠、干扰问题。一般来说，元素的特征X射线谱线数量会随着原子序数的增加而越来越多（Kα、Kβ、Lα、Lβ、Mα、Mβ、Mγ等等），并且还会出现不同衍射级别（order）的特征谱线，（元素）相互之间一定会对彼此的特征峰位判别、强度计数以及背景值测量和扣除产生不同程度的干扰，从而对测试结果的客观性和可靠性提出了严峻挑战。在常规元素电子探针分析中，某几（两）种元素不可以被同时分析的典型例子包括但不限于：（1）Na和Zn元素，Na元素在TAP晶体中的Kα谱线位置（Kα=129.473 mm）与Zn元素在TAP晶体中的Lα、Lβ谱线位置（Lα=133.211 mm、Lβ=130.265 mm）非常靠近；（2）Ti元素和V元素，Ti元素在LIF晶体中的Kα=191.205 mm，但是Kβ=174.807 mm，这与V 元素在LIF晶体中的Kα谱线位置（Kα=174.175 mm）非常靠近；（3）Pb元素和S元素，S元素在PET晶体中的Kα谱线（172.096 mm）与Pb元素的Mα谱线（169.307 mm）非常靠近，在进行两者都是微量元素含量的情况下需要非常慎重。

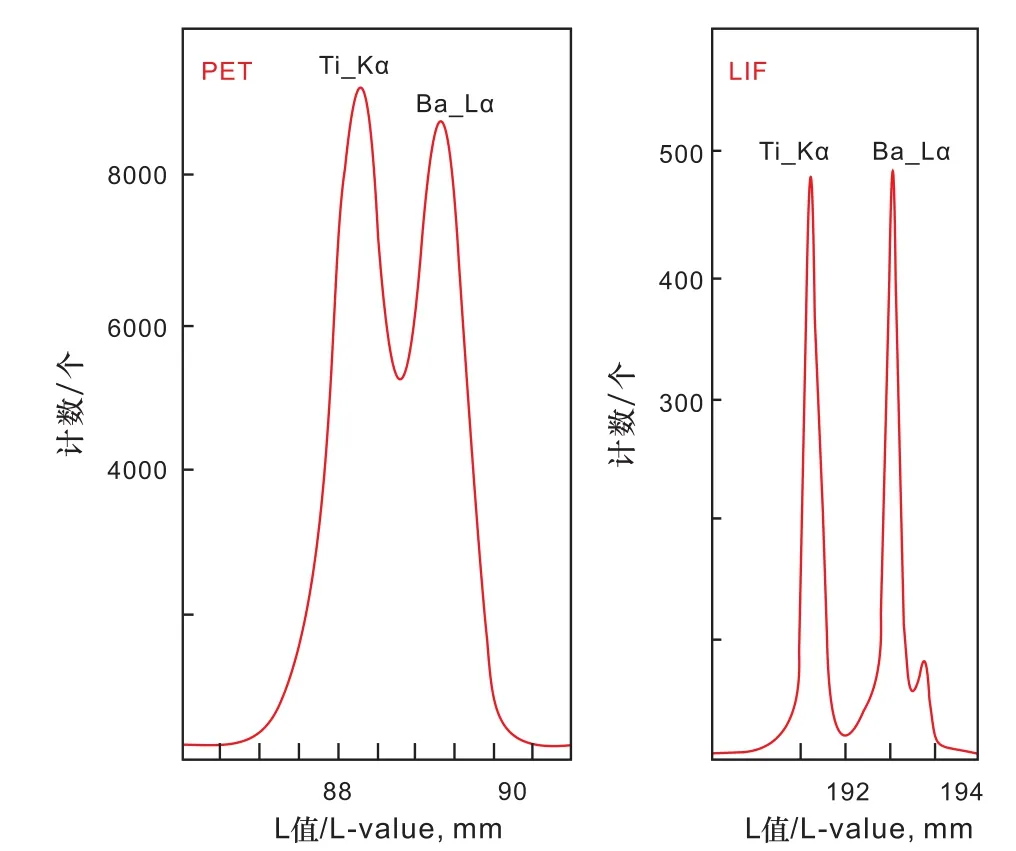
图1 电子探针波谱仪分光晶体PET和LIF对Ti（Kα）和Ba（Lα）的特征谱峰辨析能力差别示意图（BaTiO3, 15 kV,100 nA）（改自JEOL EPMA Training Program教材）Fig.1 The differences of microprobe WDS PET and LIF crystals in analyzing Ti (Kα) and Ba (Lα) characteristic X-ray spectrum(BaTiO3, 15 kV, 100 nA) (modified after JEOL EPMA Training Program textbook)

在实际工作中，通过定性分析或矿物学基本常识对被测样品的元素多样性进行识别后，必须首先确定被测量元素之间是否存在相互可能发生干扰的谱线 - 这在所有电子探针分析软件中均可以查询到（即L值或能量eV）。在微量元素测量中，因为其含量本身就比较低（<1.00 wt%），因此，即便是出现来自主量元素较弱谱线Kβ、Lβ的干扰也会导致一个明显的偏差。例如，在含F矿物（云母）和熔体的F，Cl含量测试中，Li和Hermann（2015）等人就发现F的Kα、Fe的Lα和Mn的Lα谱线特征峰位有重叠，从而采取了相应的优化措施，并改良了实验条件，且开启了PHA滤波整合模式（见下文）。同样，在稀土元素的分析中，元素重叠峰的干扰情况更加严重。因为稀土元素之间的化学性质十分接近，具有类似的外层电子结构，这就导致不同的稀土元素的特征X射线之间存在大量峰位接近的谱线，且绝大多数在技术层面都是无法被精准识别和区分的（William, 1996）。尽管研究人员随后提出了利用修正因子来规避和剥离稀土元素之间的干扰（Amli and Griffin, 1975; Roeder, 1985），并利用相应的修正算法来应用于一些比较严重的谱峰重叠情况（Donovan et al., 1993; Fialin et al., 1999），且也都取得了不错的实验结果（王汝成等，2006;Konecny et al., 2018），然而受制于分析流程的复杂性和标准物质可靠性等因素，稀土元素的分析一般只限定于解决特定科学问题上，如稀土矿物的分析（王树根，1987；Donovan et al., 2003; Jercinovic,2008; Goemann, 2011）、以及独居石等副矿物的电子探针化学定年方法中（见张文兰等，2003），且大都需要后期进行大量的优化计算处理（例如王勤燕等，2007），对研究人员的专业知识和技术能力要求颇高。

除了峰位重叠干扰问题，背景值（BG，Background）的测量与扣除也是非常关键的。一般来说，如果被测的几种元素的特征峰位靠的较近（例如±5 mm），那么就必须进行条件实验来寻找一个合理的背景值，减小可能导致的误差。例如，在主量元素测试中，以造山带与地壳演化教育部重点实验室的两台JEOL探针为例（JXA 8100和JXA8230），笔者在设立氧化物类型（11种主量元素：K、Ca、Ti、Mg、Al、Cr、Mn、Fe、Ni、Na、Si）分析程序中发现，K的背景值均可设为±5 mm（PETJ），而Ca的背景值（PETJ）在两台仪器的谱仪中则需分别设定为+1.5 mm、-1.5 mm（JXA 8100）和+1.5 mm、-1 mm（JXA 8230）。这是通过大量的条件实验，进行WDS谱仪的全谱段定性扫描，不断尝试不同的BG值对实验结果才得出的经验值。笔者认为，这应该是由于每台电子探针的谱仪构造和分光晶体的性能存在差异所导致的，因此，建议各个电子探针用户也最好通过条件实验寻找这样一个适宜的背景值。

在微量元素分析中，如何正确设定背景值则是对数据质量有非常重要的影响。首先微量元素的特征峰位的计数率一般都较低，即具有较弱的特征峰强度（高度），那么就极有可能被其他（干扰）元素的特征峰位和/或背景噪音淹没。尤其是在重金属（>Fe）元素共存的时候，情况会更明显（严重）：重金属元素可以激发出大量的特征X射线谱线（Kα、→ Mα、Mβ、Mγ），因此会大大增加错误判断微量元素特征峰的峰位及其强度计数的概率。其次，不同元素干扰（重叠）峰的存在，也对准确测量微量元素的背景值（范围）提出了更高的要求，这将直接影响微量元素的定量分析准确度（accuracy），从而导致较大的误差出现（Donovan et al., 2016）。最后，背景噪音的干扰在微量元素的测试中一般会非常明显，出现峰背比值接近1（P/B≈1）的概率会非常高，这时候，进行传统的峰位左右两点扣除计算就不是很合适了，因为此时大概率会导致该微量元素被误认为是背景噪音而被处理掉（遗漏，未被分析），或者被严重低估真实含量 - 即使只有一点点的扣除计算误差，也会导致巨大的扣除误差（Jercinovic, 2008）。针对这种情况，Merlet 和 Bodinier（1990）提出了背景值多点扣除法（multi-point background MPB method），并在随后得益于软件技术的发展被进一步完善（请参考Donovan software，http://probesoftware.com）。MPB方法可以有效识别出某种/些微量元素是否真实存在（即峰位识别困难、强度计数不明确、峰背比值趋同的情况），能够提高微量元素测试的精准度，并在实际工作中，如独居石微量元素分析得到了很好的应用（Allaz et al., 2019）。

1.3 脉冲幅度分析器（PHA）的启用

PHA的工作原理是通过设置不同的甄别电压来区分具有不同能量但是高阶线和一阶线重合的特征谱线。比较经典的例子就是对磷青铜的分析：P的Kα谱线（P_Kα=197.24 mm）与Cu的第四阶Kα谱线几乎重叠（Cu_4thKα=197.54 mm），如果不开启PHA的过滤功能，分析结果中的P含量通常会偏高近三倍，而开启PHA滤波功能后（Diff mode），P_ Kα谱线的能量正好是 Cu_4thKα谱线能量的4倍，因此，经过放大器放大后输入到PHA通道的脉冲高度是不一样的，占据了PHA不同的通道窗口：P_ Kα谱线峰位的能量分布在Hv=1～3 v的电压范围，而Cu_4thKα谱峰峰位的能量分布在Hv=6～10 v的电压范围。因此，通过设置合适的甄别电压就可以从脉冲信号上把两者区分开的（图2）。实际测试工作中，尽管在一般情况下并不需要启用PHA的滤波功能，我们还是建议对是否开启PHA的整合（Integral,Int.）或分化（Differential, Diff.）功能进行考量。这在F、Cl测试（Li and Hermann, 2015）以及金红石的Zr含量测试中（李小犁等，2017）均有应用。

1.4 标准物质的选用

标准物质的可靠性和合理选用是电子探针定量分析数是否合格的关键性前提条件。在数据预处理过程中，尽管可以利用ZAF、PRZ等修正算法进行诸如基体效应等方面的校正，系统误差与测量误差在修正过程中会发生传递并叠加到最终结果上。在微量元素分析中，由于待测元素本身含量低，即使一个原本较小的误差/偏差也会导致数据结果的可靠性降低。理论上，标准物质应该和待测物质完全一致，例如，测试橄榄石就应该使用橄榄石标样，然而在实际工作中一般很难实现。通常情况下，标准物质的选择应遵循以下两个基本原则：（1）该元素在标样物质中具有较高的绝对含量；（2）标准物质与待测样品的晶体化学类型完全一致，或者至少非常近似（氧化物、硫化物、金属化合物等）。如果二者不可同时满足，如元素在某标准物质中含量较高，但类型上与待测物质不一致（氧化物 vs.金属化合物），那么一般选择含量最高的物质为原则为佳。

图2 电子探针PHA功能示意图Fig.2 Microprobe PHA function sketch

在实际测试工作中，如何选择合适的标准物质大都需要条件实验的验证。在主量元素测试中，例如，在进行Na和Al的测试时，我们实验室一般采用硬玉（NaAlSi2O6）作为标准物质，这对大多数的硅酸盐类矿物是适宜的，但是却并不适用于Al2SiO5（蓝晶石）的分析。这可能是因为后者较高的Al含量引起的基体效应更显著所致，因此选用单质Al或者刚玉（Al2O3）作为测试Al的标样会更合适。类似的，在Fe的测试中，一般采用赤铁矿（Fe2O3）或黄铁矿（FeS2）作为标样，但是在钛铁氧化物的测试中却并不适用，这时使用单质Fe作为标准物质更合适，其结果大多不需要进行脱机校正（offline correction）就能得到一个总量合适、原子比例适当的输出。在微量元素测试中，如Co、Ni、Zn等元素，其相应的氧化物或硫化物、甚至金属化合物标准物质比其单质会更适宜，这在陨石矿物学的分析中比较常见（例如Sharygin et al.,2020）。类似的情况也出现在稀土矿物的测试中，相应的标准物质可选择稀土的硅酸盐玻璃、磷酸盐矿物、稀土硼化物等等天然或合成化合物（王树根，1987；邱巨峰等，1992；Donovan et al., 2003;Hetherington et al., 2008; Allaz et al., 2013 ），这个时候就需要针对具体的分析任务-待测样品晶体化学类型、稀土元素预估含量、是否有Th-Pb等元素干扰等情况进行判断，选择合适的标准物质标定。

最后，标准物质还可以用作（二次）平行标样，当成未知样品加入到待测样品的分析序列中，通过检验标准物质在此次实验条件下的测试结果与其理论结果是否一致来判断未知样品分析结果的可靠性。我们建议，任何类型的电子探针定量分析都应该在实验前或后，甚至中间加入标准物质作为平行样品对测试过程进行监测，这在诸如质谱仪分析的实验中就得到了很好的引入。尽管电子探针的实验条件一般更稳定和更抗干扰，在海量实验分析任务的情况下，加入平行试样可以大大提高数据可靠性检查的效率。

1.5 其他需要注意的情况

在电子探针微量元素分析中，通过加大电流（或加速电压）和延长分析时间的方法一般是可以提高待测（微量）元素的检测极限（D.L.,Detection Limit），并降低标准偏差（S.D., Standard Deviation），但是此时带来的间接危害却是对样品的物理损伤，导致测试无效（如果样品因为电子轰击分解，自然是无法获得样品完整的成分信息的）。比较典型的例子包括石英中Ti、Al等微量元素含量的分析（Cui et al., 2019）、磷灰石中F、Cl、P的分析（见Li and Hermann, 2015）、以及独居石等副矿物的CHIME定年分析（Suzuki and Kato, 2008）等等。类似的情况同样也出现在主量元素的分析中，如在对含碱金属的矿物（白云母、钠长石、玄武岩玻璃、长英质熔体等）以及碳酸盐（方解石）和含水矿物等等的测试中。这个时候，通常可以通过加大束流束斑的办法降低激发电流对待测样品的损害，比如调节束斑直径到10～100 μm或更大，并对标定的标样数据进行合理调整。但是这样做的前提条件是，待测样品成分必须均匀且粒度合适，并且在进行基体效应校正计算时，最好避免采用ZAF修正法（吸收效应的修正对微量元素的误差一般比较大）。与此同时还应该注意，增加束斑大小后，主量元素的测试可能会出现较大误差。

为了增加微量元素的信号采集率，我们还可以进行硬件上的参数调整，如更改谱仪探测器的窗口缝隙（detector slit），提高探测器的分辨率，以此增强信号强度。以JEOL系列电子探针为例，出厂设置一般为最小值（100 μm），可有三档范围的调整，最高档为300 μm的缝隙宽度（具体参数请参看电子探针的随机说明书）。只是这个时候需要注意的是，如果主量元素也需要同步分析时，那么极有可能导致相当程度的（主量元素）误差。因为此时的分析条件与使用标准物质进行标定的条件完全不同（硬件环境），会导致标定数据（Standard Data）并不适用于当前的定量分析任务，因此只限定于特殊的低含量的分析，例如在Fe3+的Flank Method分析测试中（李小犁等，2019；Li et al.,2018），对该参数进行调整，单独进行价态铁的定量分析。

2 数据合法性判断

电子探针定量分析结果揭示的是元素在物质中的丰度。历史沿袭中，我们习惯用质量百分数来表述丰度（wt%，×10-6等），这是一种比较方便和直观的计量标准。但是，电子探针分析的物理基础是电子和轨道电子的交互作用，涉及到的是有多少个数量的原子参与了该物理过程（激发态—基态—特征X射线等能量释放）。因此，这时用质量分数来表达浓度计量就不是很合理，相反，应该用原子的摩尔数百分比，或原子百分比（atomic proportion）及（原子）离子比值来说明元素在物质中的丰度信息。这时因为，特征X射线的产生取决于参加物理作用的原子个数，而X射线的强度与质量分数之间并没有坚实的物理联系，这与以质谱仪为代表的利用质量分馏的分析仪器完全不同，所以，在电子探针分析中采用质量分数表达元素丰度并作为结果输出需要谨慎对待，这使得原本有规律的现象失去了其客观性（徐萃章，1990）。

在常规电子探针分析中，原子摩尔分数（比值）能够反映晶体化学的比例关系，这是判断物质成分的重要信息，而非原子质量分数。例如，在石榴子石的测试中经常会得到总量（Total）的波动范围可以从96 wt% 到 104 wt%；在实验条件和仪器状态稳定的条件下，这样的结果输出并非意味着测试结果的不准确，或者是由于样品蚀变所致。此时更关键的判断依据应该是结果中的Si : O比值是否满足1:4的晶体化学标准（石榴子石通用化学式：A3B2[SiO4]3），即Si的摩尔（原子）百分比是否满足0.25±0.02%的条件。如果并不满足，那么就需要进一步思考是否是测试出现了问题，或者揭示了更重要的成因信息（Si:O>0.25，高硅钙铁石榴子石Majorite类型，Smith and Mason, 1970）。至于为何石榴子石的测试结果经常会出现总量无法完美符合100±2 wt%，原因可能是多方面的，如石榴子石成分的多样性（镁铝榴石、钙铝榴石、钙铁榴石等等）以及其中价态Fe的影响，或者是由于石榴子石致密的晶体结构都有可能，目前暂无可靠合理的解释。在微量元素的电子探针分析中，某些微量元素可能并不参与到物质的晶体结构中去，而是以其他游离态等非结构性赋存态存在于物质中，这时用质量分数来表述其在物质中的丰度是可以接受的。不过，在探讨物质晶体化学成分的时候，是需要计算物质（矿物）中的元素配位数以及单位原子个数（pfu, per formula unit），那么这时微量元素的摩尔百分比分数是有意义的。

在电子探针定量分析实验中，往往会通过完成一定数量的数据（N个数据）来证明笔者的观点和讨论所需的论据。实际工作中，每次的测试结果一定是在某个区间内有波动的，这既有可能是由于测量的误差，也有可能是被测试物质本身的原因。并且，波动的范围一定是与所测试的数据样本数量多少有关的：一般说来，随着数据量的增加，结果的波动程度一般也会更明显，出现不断更新的极大、极小值，且相应的平均值会越来越会趋向于在某个“固定”的范围（值）内波动。一般来说，数据量越多，所得的平均含量可能越接近真实值，那么这里我们需要回答一个问题：需要多大的数据量得到的平均含量才能客观真实反映该元素在物质中的丰度呢？

例如，在金红石Zr温度计的研究中，有学者发现，当分析数量超过100个数据以上时，才可以得到一个符合我们观察的结果（李小犁等，2017；Jiao et al., 2011）；但是，也有研究人员通过测试仅仅20～30个数据就可以判定一个客观事实（Pape et al., 2016）。再举一个例子，在热液矿床硫化物Au和Ag含量分析中，在实验条件稳定的情况下，在同一个矿石中的相同硫化物（白铁矿）里，可以得到含量差异巨大的Au含量结果（0.00～2.00 wt%） （Li et al., 2010）。尽管Au在白铁矿（以及其他硫化物中）的赋存态还有待进一步探讨，或许是游离态的非晶格结构存在。在此我们更希望知道，该矿石中Au的真实平均含量应该在什么范围？是否具有工业开采价值？并且需要多少数据量的电子探针分析才可以获得？

为解决这个问题，可以采用统计学中的随机迭代计算方法。具体的操作是：在完成若干数据量分析后（N个数据），把所有数据进行随机排列组合，分为若干组（例如3组或者5组，或更多）。在每一组中，对排在前面的n个数据（n≧2）进行平均值C的计算，C1=(N1+N2)/2，C2=(N1+N2+N3)/3，……，CN=(N1+N2+N3+……+ Nn)/n，然后把这些平均值进行曲线分布作图。这样，对所有随机排列的组（3组或5组）都进行类似计算，以数据量N为X轴，每个N值下计算所得的平均值CN为Y轴做曲线图，得到若干条（3条或5条）具有不同震荡规律的曲线分布。在所有的这些曲线分布图中，平均含量C一定是随着数据量N的增加而趋向某个比较固定值的；而且当数据量N达到某个阀值M后（N=M），C值（CM）不会再随着数据量的继续增加而发生明显改变，那么，该阀值M就是该样品分析所需的最小数据量，而CM值就是该（微量）元素在物质中的合法平均含量（图3）。通过上述随机迭代计算得出的最小分析数据量及平均含量具有统计学意义上的客观性，在探讨相关科学问题的时候是具有说服力的。实际应用中，笔者已经在洋底黑烟囱硫化物（白铁矿等）的Au、Ag含量（品位）的讨论中（Li et al., 2010），以及中高温榴辉岩中金红石的Zr含量及相关温度计应用中（李小犁等，2017）就此展开了相关研究，确保了相关科学问题不会因为数据样本的有限性可能导致的结论偏差（即数据量不够引起的伪迹），同时也避免了进行海量数据分析的浪费和非必要性。该方法主要用于证明本次实验分析的样本数量是合理的，并且由此计算得出的元素的平均含量是具有统计学上客观性的。至于是否可以用于对仪器系统误差或者测量（随机）误差进行讨论，还有待大量实验工作的验证和探讨。

3 总结与思考

电子探针分析具有快速、无损、微区、原位、高精度、高准确度、高分辨率，高灵敏度的技术特征，是现代科学发展研究中非常重要的技术手段。而且相比其他分析化学技术，操作流程简单且成本较低，同时对测试样本的制备要求也不高。电子探针定量分析反映的是物质中元素丰度的“数量”信息，并非元素的“重量”或者“质量”。因此，历史约定俗成使用质量百分比来来表达元素丰度并不具有合法性。事实上，在一些项目测试中，即便实验条件都合格稳定，最后的定量分析结果的数据总量（Total值）也是有可能会>100 wt%，这并非违反了基本的物质定律，而是需要首先思考的是样品本身的特性。因此，实际工作中，更应该关注分析结果中的摩尔分数比值（或原子比），是否正确反映了被测样品的晶体化学特征——如是否满足Si:O= 4:1这样的原子比关系（橄榄石、石榴子石），来判断数据的合法性，而非简单地仅仅依据数据的质量分数总和。尽管在快速的、初步的数据质量检查中可以参考，但绝不是唯一的依据。

电子探针定量分析结果的准确度在很大程度上取决于标准物质的选用和标定。标准物质的选择理论上应该和待测样品完全一致，但由于在实际工作中很难实现，因此，应至少遵循含量较高的和近似晶体结构类型两个标准来选择标准物质，最大程度避免基体效应及修正过程（曲线修正、ZAF修正、PRZ修正等）的误差、偏差传递。与此同时，应该考虑把标准物质作为平行样品加入未知样品的测试序列，以此来监测实验结果的稳定性，确保数据的可靠性。

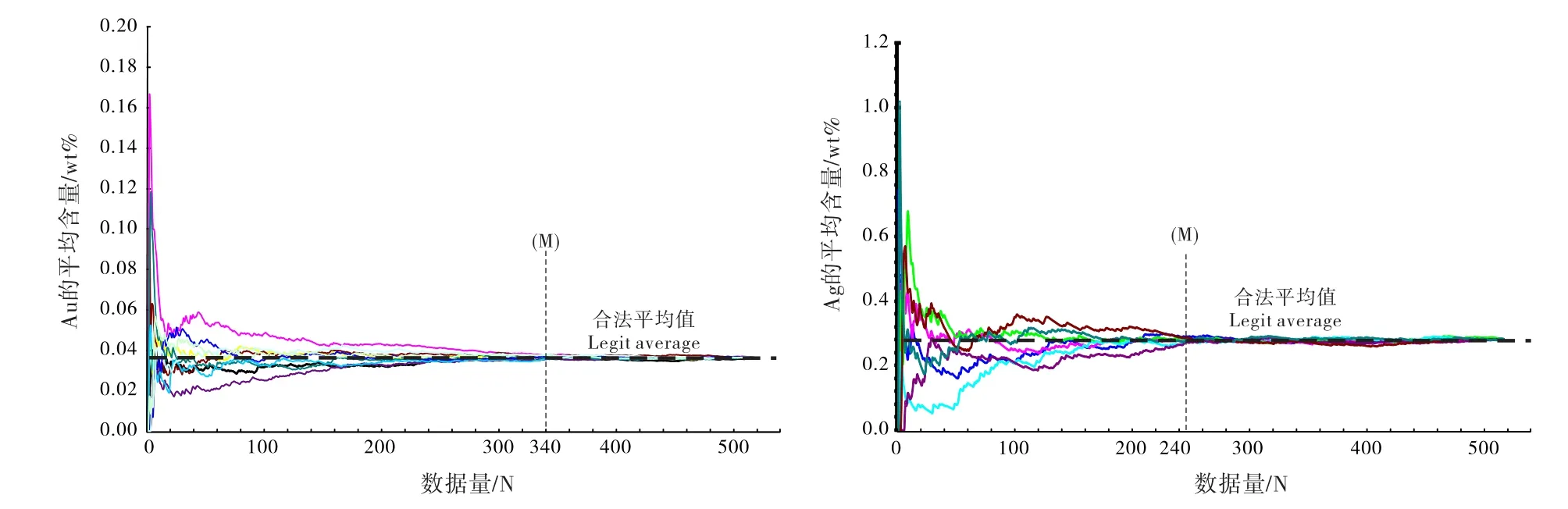
图3 电子探针分析数据样本量N与白铁矿中Au和Ag的平均含量值（CN）变化关系曲线示意图（详情见正文）Fig.3 Correlation diagrams between the microprobe analyses quantity N and the average contents of Au and Ag in marcasite (CN) (see in the text)

在实际工作中，电子探针定量分析的最大技术难点在于干扰重叠峰的厘定和辨析。首先，这需要进行一个全元素的定性分析，确定存在的元素种类；其次，通过特征X射线谱线数据库查询，去寻找潜在的干扰重叠峰位——包括1阶和多阶谱线。如果两个或以上元素之间在同一个晶体中的L值相差小于5 mm，那么就有峰位相互干扰重叠的风险，须仔细研判和规避。同时，还需要设定合理的BG背景值，这可以通过条件实验来寻找，并且根据具体情况进行背景值扣除计算的优化。需要提醒是，尽管电子探针功能强大，理论可分析元素种类非常多，但是这并不意味着每种元素都可以得以高质量、高精准的测试，切不可求大求全，试图对所有可能存在的微量元素都进行定量分析。比较稳妥和合理的电子探针分析方案应当尽量减少待测元素 （尤其是微量元素的种类），求稳求精。每一种分析化学仪器都有它擅长和不擅长的领域，所以在具体工作中，必须首先明白需要解决的科学问题是什么，再去选择最佳的技术手段。不要因为电子探针强大性能而过度依赖，包括在波谱分析（WDS）还是能谱分析（EDS）的选择上。在当今各类分析技术日新月异的大环境下，特别是高精度（激光）质谱仪的出现，在测试微量元素方面会更有优势，是电子探针分析的有力补充和拓展。技术上的可行（理论）与获得可靠的分析结果（实际）对应的是完全不同的诉求。

最后，在电子探针定量分析中，往往需要面对这样一个实际问题：需要完成多少样本数的测试分析？这对于地质样品分析尤其重要，因为大多数的地质样品都存在局部/微区范围的成分不均匀，从而导致每次分析结果都会有一定的波动，特别是对微量元素的分析，从而影响到我们对微量元素在某物质（矿物）中平均含量的考量。为解决这个问题，可采用迭代计算方法，避免因单个测试所得一个极大或极小值最后影响到平均含量的正确评估。这也可以避免海量数据测试的浪费和非必要性。该方法可以在一些特定的科学问题研讨中起到关键重要，包括但不限于微量元素温度计以及矿石中贵金属元素品位的分析。

致谢：本文为固体地球科学重点实验室联盟2020年实验技术与应用年会（南京）学术报告论文，并受到南京大学内生金属矿床成矿机制研究国家重点实验室张文兰教授的热情指导。初稿得到两位匿名审稿人的评审，对本文的进一步完善起到了积极建设性的作用，在此表示真诚的感谢！