基于粒子群算法的LCLC谐振变换器优化设计

赵 斌 王 刚*② 宋婧妍② 刘雅琳

①(中国科学院空天信息创新研究院高功率微波源与技术重点实验室 北京 100190)

②(中国科学院大学 北京 100039)

1 引言

空间行波管放大器(Traveling-Wave Tube Amplifier， TWTA)广泛应用于雷达、电子对抗以及卫星导航等应用中，起到微波功率放大的作用[1]。空间行波管放大器由两部分构成：电子功率调节器和空间行波管。电子功率调节器为空间行波管的正常工作提供合适的高电压[2]，因此，电子功率调节器的效率将直接影响整个空间行波管放大器的效率[3，4]。提高电子功率调节器的效率，对于降低卫星上太阳能电池板的数量，降低发射重量，具有重要的意义。

当前，如图1所示，电子功率调节器普遍采用2级结构：第1级为Buck变换器[5]，第2级为LCLC谐振变换器[6]。目前，由于Buck变换器已经得到了广泛的研究，因此，本文主要研究LCLC谐振变换器[7，8]。第2级LCLC谐振变换器，将Buck变换器的输出电压，升压为行波管所需要的高电压，并提供电气隔离的功能。然而，如图1所示，LCLC谐振变换器具有4个谐振参数，Lr为变压器漏感；Cs为串联谐振电容；Lm为变压器励磁电感；Cp为并联谐振电容(即变压器寄生电容)，增加了LCLC谐振变换器总损耗优化的难度。因此，当前，LCLC谐振变换器的设计主要依赖经验，无法对LCLC谐振变换器的总损耗进行优化。

近年来，粒子群优化设计算法在功率变换优化设计中得到了广泛的应用[9]。粒子群优化算法从随机解出发，通过适应度评价解的品质，并通过多次迭代搜索最优值求得最优解[10，11]，具有精度高优化以及收敛快等优点[12，13]。本文将粒子群优化设计算法应用到LCLC谐振变换器中，提出了一种基于粒子群优化设计算法的LCLC谐振变换器优化设计方法。该优化设计方法以LCLC谐振变换器的总损耗为优化设计的目标函数，通过粒子群优化算法，求得总损耗最低时的LCLC谐振变换器的谐振参数(Lr， Cs， Lm和Cp)。基于总损耗最低时的谐振参数，搭建LCLC谐振变换器，最终实现LCLC谐振变换器的高效率。

本文按照如下的思路展开：第2节通过对LCLC谐振变换器工作原理的分析，推导了LCLC谐振变换器总损耗的公式；第3节基于LCLC谐振变换器的总损耗公式，提出了基于粒子群优化算法的LCLC谐振变换器优化设计方法，并给出了例子；第4节基于第3节中的例子，搭建了优化设计的LCLC谐振变换器，并进行了一系列实验，用于验证本文提出的优化设计方法；第5节对本文进行了总结。

2 LCLC谐振变换器总损耗分析与计算

在本节中，基于LCLC谐振变换器的工作原理[14]，对LCLC谐振变换器的总损耗进行了计算。在空间行波管放大器的应用中，由于LCLC谐振变换器工作在零电流、零电压条件下，因此，开关管无开通和关断损耗。LCLC谐振变换器的损耗包含开关管驱动损耗、开关管的导通损耗、串联谐振电容损耗、变压器铜损、变压器铁损、变压器介质损耗以及整流二极管损耗。下面将分别对各部分损耗进行计算，并推导得到LCLC谐振变换器的总损耗公式。

2.1 高压整流二极管损耗

在LCLC谐振变换器中，为降低整流二极管损耗，采用碳化硅二极管，因此，反向恢复损耗可以忽略。高压整流二极管的损耗为导通损耗，即

其中，PD为高压整流二极管损耗，Vo为LCLC谐振变换器的输出电压，VD为高压整流二极管的管压降，Ro为变换器负载。

2.2 主开关管驱动损耗

主开关管的驱动损耗为

其中，Qg为门极驱动电荷，Vdr为开关管的驱动电压，fs为LCLC谐振变换器的谐振频率。

2.3 主开关管的导通损耗

由于在空间行波管放大器应用中，主开关管实现了零电压、零电流导通和关断，导通损耗和关断损耗降为0。导通损耗为

其中，Irms为谐振电流有效值，Ron为主开关管的导通电阻。

结合谐振电流有效值的计算公式[14]，主开关管的导通损耗为

其中，Vo为LCLC谐振变换器输出电压，Ts为开关周期，Trs为Lr和Cs的谐振周期，Ro为负载，a为变压器变比。

2.4 主变压器铜损

由于LCLC谐振变换器工作在高频条件下，引起变压器绕组的邻近效应和趋肤效应，从而加剧了变压器的铜损。变压器的铜损为

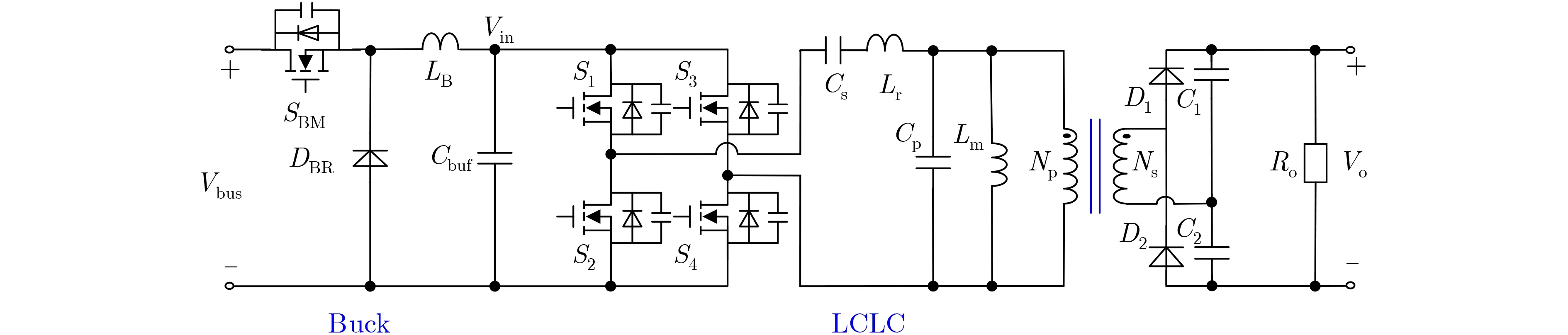
图1 电子功率调节器的两级结构

其中，Rac为变压器的交流电阻。

2.5 主变压器介质损耗

在空间行波管放大器的应用中，输出电压从数千伏到一万多伏不等；此外，LCLC谐振变换器工作在高频条件下，变压器的寄生电容在每个开关周期都要进行充放电，从而引起介质损耗。主变压器的介质损耗为[13]

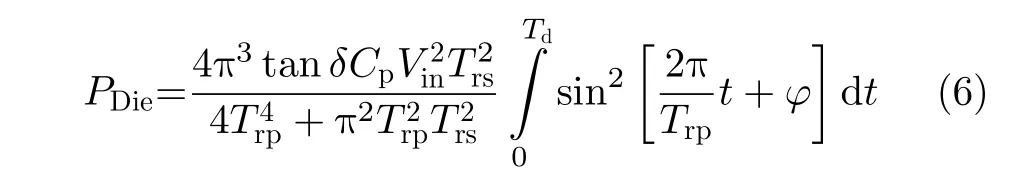
其中，δ为介质的损耗角，Trp为Lm和Cp的谐振周期，Td为死区时间，φ 为一常数。

2.6 变压器磁芯损耗

变压器在工作中，除具有铜损和介质损耗之外，磁芯也将产生损耗。在LCLC谐振变换器中，磁芯损耗为

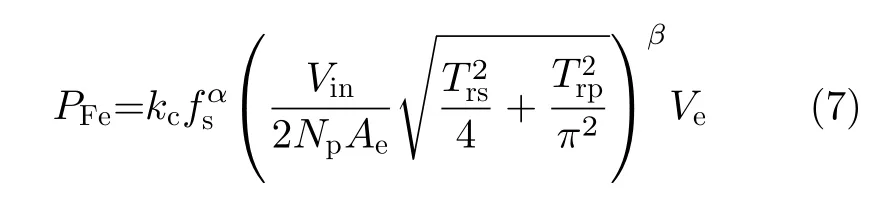
其中，kc，α，β为磁芯材料损耗参数，Ve为磁芯体积。

2.7 LCLC谐振变换器总损耗

结合式(1)—式(7)，得到变换器的总损耗为

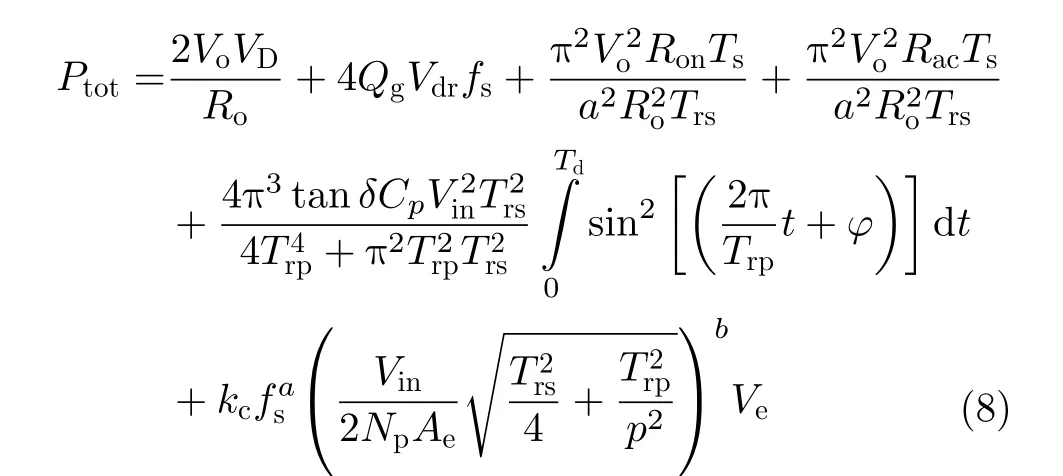
在接下来的优化设计中，将式(8)作为优化目标，进行LCLC谐振变换器的优化设计。

3 基于粒子群优化算法的LCLC变换器优化设计

由于在LCLC谐振变换器中具有4个谐振参数，即漏感、串联谐振电容、变压器励磁电感以及变压器寄生电容，因此，LCLC谐振变换器的优化设计比较困难。本文结合当前的人工智能算法和粒子群优化算法，提出了基于粒子群优化算法的LCLC变换器优化设计方法。

3.1 LCLC谐振变换器优化设计方法

基于粒子群优化算法的LCLC变换器优化设计方法的流程图如图2所示。优化设计算法分为以下几步：

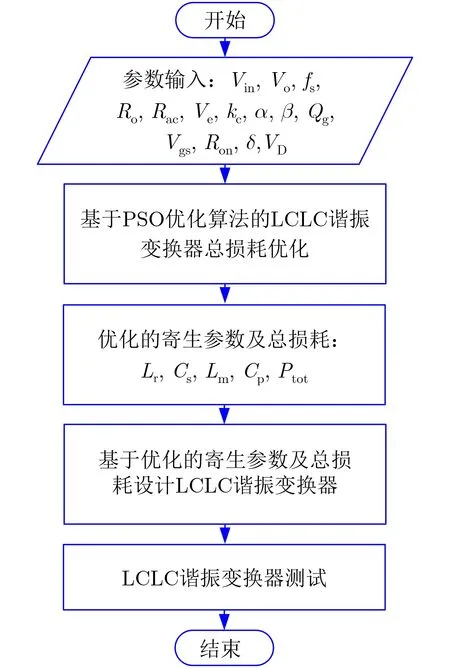
图2 基于粒子群优化算法的LCLC谐振变换器优化设计

步骤 1 在LCLC变换器优化设计开始之前，根据LCLC谐振变换器的输入电压、输出电压、工作频率，确定主开关管、整流二极管型号，并选定磁芯形状和材料。并根据主开关管的参数、整流二极管参数、磁芯的参数，代入变换器总损耗公式中。

步骤 2 采用粒子群优化设计算法，对LCLC谐振变换器的总损耗进行优化，计算得到优化的谐振参数以及优化的总损耗。粒子群优化算法将在3.2节中详细阐述。

步骤 3 基于步骤2中的优化的寄生参数，搭建LCLC谐振变换器。

步骤 4 对LCLC谐振变换器进行测试。

3.2 用于LCLC谐振变换器优化设计的粒子群优化设计算法

用于LCLC谐振变换器优化设计的粒子群优化设计算法流程图如图3所示，包含以下几步：

步骤 1 粒子群优化算法初始化。粒子群优化算法的参数，包含Weight.start， Weight.end，kind和Vel.max被初始化。其中，粒子的个数Npa为20，最大的迭代次数Max.Iteration是100。

每一个粒子被赋予任意的Lr， Cs， Lm和Cp值。LCLC谐振变换器的参数输入到粒子群优化设计算法中，变换器总损耗作为粒子群优化算法的目标函数。

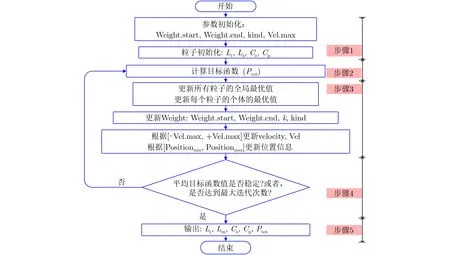
图3 用于LCLC谐振变换器优化设计的粒子群优化设计算法

步骤 2 总损耗计算。在这步中，计算每个粒子的目标函数值及变换器总损耗。目标函数值将用于评价每个粒子的适应度。

步骤 3 更新全局最优值、个体最优值、Weight和Vel。基于步骤2中计算的总损耗，所有粒子的全局最优值，每个粒子的个体最优值，Weight和Vel将被更新。

步骤 4 重复步骤2和步骤3，直到满足循环结束条件。如果平均目标函数值稳定，或者达到最大迭代次数，循环过程将被终止。否则，将重复步骤2和步骤3的过程。

步骤 5 输出优化的谐振参数值以及优化的总损耗。当步骤2和步骤3的循环终止条件满足之后，粒子群优化算法将输出优化的谐振参数值以及总损耗。

至此，粒子群优化算法结束。当粒子群优化算法结束之后，将得到优化的谐振参数，包含Lr， Cs，Lm和Cp。接下来，将利用优化的谐振参数，搭建LCLC谐振变换器，并进行实验测试。

3.3 粒子群优化算法验证

在3.1节和3.2节中，分别针对基于粒子群算法的LCLC谐振变换器优化设计方法以及粒子群优化算法进行了阐述。本节将采用基于粒子群算法的LCLC谐振变换器优化设计方法，进行LCLC谐振变换器的优化设计，以此验证本文提出的优化设计方法。

LCLC谐振变换器的参数如表1所示。输入电压为40 V，输出电压为4800 V，开关频率为300 kHz，输出功率为300 W。基于LCLC谐振变换器的输入、输出电压以及开关频率，磁芯选择TDK公司的FEE38/16/25，磁芯材料为N87，适于工作在500 kHz以下的开关频率。此外，主开关管选择RJK6505PBF。

表1 LCLC谐振变换器参数

基于表1的参数，采用本文提出的基于粒子群算法的LCLC谐振变换器优化设计方法，对LCLC谐振变换器的总损耗进行了优化设计。LCLC谐振变换器的总损耗，随迭代次数的变化如图4所示。

由图4可以看出，随着迭代次数的增加，变换器总损耗逐渐稳定，最终优化得到的总损耗为8.9 W，对应的谐振参数为Lr= 0.09 μH， Cs=1 μF， Lm= 8.0 μH， Cp= 13.2 nF。当LCLC谐振变换器的优化过程完成之后，第4节将基于优化结果，搭建LCLC谐振变换器并进行实验测试。

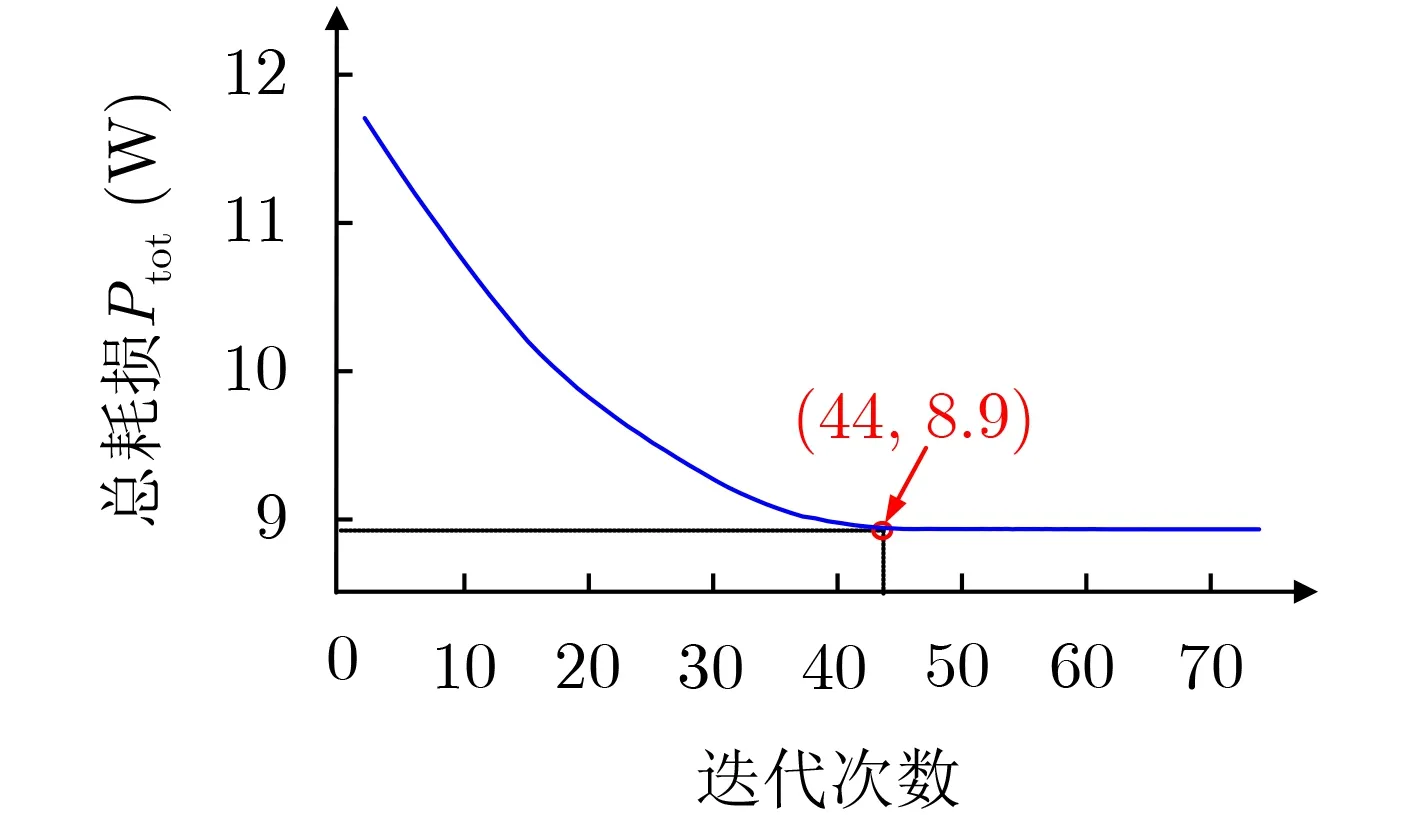
图4 总损耗随迭代次数的变化

4 实验验证

在本节中，首先，基于第3节的优化设计结果，搭建了优化的LCLC谐振变换器；其次，在优化的LCLC谐振变换器搭建完成之后，进行了一系列实验，验证了本文提出的优化设计方法的有效性；最后，在改变输入电压和输出功率的情况下，测试了LCLC谐振变换器的效率。

4.1 LCLC谐振变换器

基于第3节优化设计得到的谐振参数，搭建了LCLC谐振变换器。由于改进用于高压平面变压器的部分交错绕组结构具有低漏感、低寄生电容以及低交流电阻的优势，本文的高压变压器采用了这种结构[15]。改进的用于高压变压器的部分交错绕组结构如图5所示。

变压器以及绕组的尺寸如表2所示。

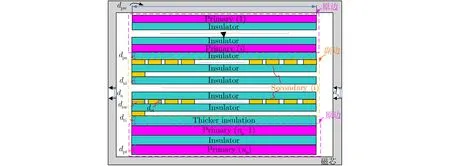
图5 改进的用于高压平面变压器的部分交错绕组结构

根据表2所示的尺寸，在Ansys Maxwell中搭建了高压变压器模型，并进行了有限元仿真。仿真得到的漏感、励磁电感以及寄生电容如表3所示。

表2 高压平面变压器参数

表3 仿真结果与优化结果的对比

由表3可以看出，与优化的谐振参数相比，仿真结果的误差可以接受。因此，LCLC谐振变换器的优化设计结果得以实现。需要指出的是，由于Cs为分立器件，优化的串联谐振的电容Cs值，可以直接通过选择分立电容实现。

4.2 基于粒子群算法的LCLC谐振变换器优化设计方法验证

LCLC谐振变换器的测试波形如图6所示。其中，vds1(t)为开关管S1的漏源极电压，ir(t)为谐振电流，vgs1(t)为主开关管S1的驱动电压，vd1(t)为倍压整流二极管D1的电压，id1(t)为倍压整流二极管D1的电流。

主开关管S1的实验波形如图6(a)所示。由图6(a)可以看出，在主开关管开通时，谐振电流ir(t)为零，同时，开关管S1上的电压vds1(t)也为零，因此，主开关管实现了零电压、零电流开通。同理，当主开关管关断时，谐振电流ir(t)为零，同时，开关管S1上的电压vds1(t)也为零，因此，主开关管实现了零电压、零电流关断。综合上述讨论，主开关管S1实现了零电压、零电流开通和关断。

图6 优化的LCLC谐振变换器的实验波形

倍压整流二极管D1的实验波形如图6(b)所示。由图6(b)可以看出，在倍压整流二极管D1开通时，谐振电流id1(t)为零，同时，倍压整流二极管D1上的电压vd1(t)也为零，因此，倍压整流二极管D1实现了零电压、零电流开通。同理，当倍压整流二极管D1关断时，谐振电流id1(t)为零，同时，倍压整流二极管D1上的电压vd1(t)也为零，因此，倍压整流二极管D1实现了零电压、零电流关断。综合上述讨论，倍压整流二极管D1实现了零电压、零电流开通和关断。

基于上述实验结果可以看出，主开关管和倍压整流二极管都实现了零电压、零电流开通和关断。

为进一步测试本文提出的优化设计方法的有效性，分别测试了当励磁电感Lm和串联谐振电容Cs改变时的波形效率。

改变励磁电感得到的实验波形如图7所示。如图7(a)和图7(b)对应的励磁电感分别为29.3 μH以及4.0 μH。测试得到的效率如图7(c)所示。

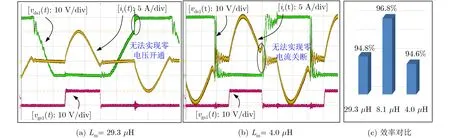
图7 改变励磁电感时的测试波形

由图7可以看出，当励磁电感Lm偏离优化值之后，LCLC谐振变换器的零电压、零电流开通和关断特性将消失：当励磁电感大于优化值时，主开关管无法实现零电压开通，此时将引起开通损耗；当励磁电感值小于优化值时，主开关管将无法实现零电流关断，此时将引起关断损耗。由效率对比的结果可以看到，在励磁电感的优化点，LCLC谐振变换器的效率最高，从而证实了本文所提的优化设计方法的有效性。

改变串联谐振电容得到的实验波形如图8所示。如图8(a)和图8(b)对应的串联谐振电容分别为0.3 μF和1.6 μF。测试得到的效率如图8(c)所示。

由图8可以看出，当串联谐振电容Cs偏离优化值之后，LCLC谐振变换器的零电压、零电流开通和关断特性将消失：当串联谐振电容Cs小于优化值时，主开关管无法实现零电压开通，此时将引起开通损耗；当串联谐振电容Cs大于优化值时，主开关管将无法实现零电流关断，此时将引起关断损耗。由效率对比的结果可以看到，在串联谐振电容的优化点，LCLC谐振变换器的效率最高，从而证实了本文所提的优化设计方法的有效性。

由上述实验可以看出，采用本文提出的基于粒子群算法的LCLC谐振变换器优化设计算法，主开关管和整流二极管都实现了零电压、零电流开通和关断。此外，与非优化的参数相比，优化的LCLC谐振变换器可以实现更高的效率，从而验证了优化设计方法的有效性。

在空间行波管放大器中，由于输入电压和负载在变化，因此，需要进一步研究LCLC谐振变换器在不同输入电压和负载时的变换器效率。

图8 改变励磁电容时的测试波形

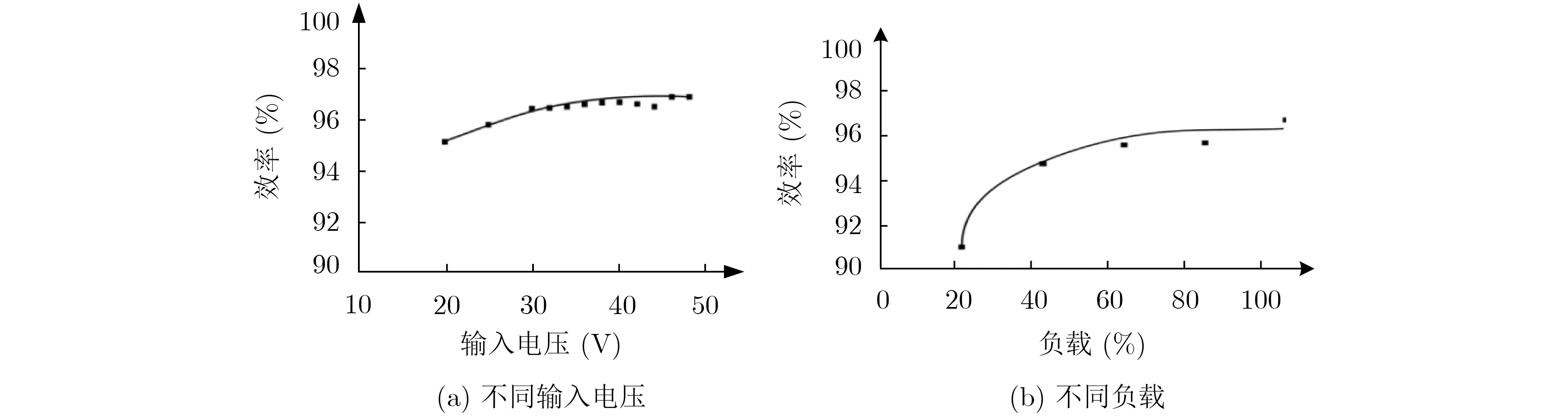
图9 效率测试

4.3 优化的LCLC谐振变换器在不同输入电压和负载时的性能

在空间行波管放大器中，由于输入电压和负载在变化，因此，需要进一步研究LCLC谐振变换器在不同输入电压和负载时的变换器效率。

优化的LCLC谐振变换器在不同输入电压条件下的效率如图9(a)所示。在额定输入电压40 V条件下，变换器总损耗为9.2 W，效率为96.8%。本文提出的优化设计方法计算得到的总损耗为8.9 W，这与实验测试结果高度一致。变换器效率随着负载的变化如图9(b)所示，由图9(b)可以看出，在宽负载范围内，LCLC谐振变换器都可以实现高效率。

5 结论

本文提出了一种用于空间行波管放大器的基于粒子群算法的LCLC谐振变换器优化设计方法。这种优化设计方法的目标，是实现LCLC谐振变换器的低损耗、高效率。首先，推导了LCLC谐振变换器的总损耗公式；然后，以该总损耗公式为目标函数，基于粒子群算法进行优化设计，得到了优化的谐振参数以及优化的总损耗；最后，基于优化的谐振参数以及优化的总损耗，搭建优化的LCLC谐振变换器，并进行实验测试。理论分析以及实验结果均表明，基于粒子群算法的LCLC谐振变换器优化设计方法，能够用于LCLC谐振变换器的优化设计，提高变换器效率。