变压器相间磁场对绕组受力的影响研究

邹德旭 钱国超 井永腾 张森鹏 张弛

（1.云南电网有限责任公司电力科学研究院 2.沈阳工业大学）

0 引言

随着电力行业的不断发展，对于电网中重要设备之一变压器受力情况的精确分析变得越发重要，其设计结构的可靠性直接影响电网的安全运行[1-3]。现阶段计算变压器绕组所受的电动力多采用对单一绕组进行受力分析而忽略其相邻绕组对其产生的影响。因此，本文针对三相变压器相间磁场对绕组受力的影响进行研究。

本文对一台SFSZ9-40MVA/110kV电力变压器的磁场和结构场进行了数值分析[4]，通过对比相间磁场是否考虑两种工作情况下绕组最大轴向力和辐向力的发生时刻变化，提出了一种绕组受力分析的新思路，对于降低电网变压器损坏概率和提升电网安全运行能力具有重要意义。

1 变压器相间磁场分析模型

本文在分析变压器相间磁场相互影响时，建立如图1和图2所示分析模型[5]，图中所示区域为变压器铁窗内相邻两相高低压绕组截面。

图1中以铁心窗左下角位置建立直角坐标系，水平位置为x轴，纵向为y轴；序号1为受相间磁场影响位置，其坐标为（x2，y2）；序号2为序号6处电流作用在序号1处的磁密矢量；序号3为低压绕组截面；序号4为高压绕组截面；序号5为铁心窗内窗壁；序号6为绕组内矩形微单元，面积为dxdy，其中心位置用(x1,y1)表示；序号7为以(x1,y1)为圆心，以(x1,y1)到(x2,y2)之间距离为半径所画圆弧曲线。

图1 分析模型1

图2 分析模型2

图1和图2中θ为arctan(|y1-y2|/|x1-x2|)，即连接(x1,y1)到(x2,y2)的直线与水平线的夹角，取值范围为（0°～90°）。

对相间磁场分析过程如下：假设在铁窗内对左侧高低压绕组施加激励，且方向为低压垂直向外，高压垂直向内；则可将左侧高低压绕组截面微分成无限多个微单元，并以(x1,y1)为圆心，以(x1,y1)到(x2,y2)之间距离为半径所画圆弧曲线，由于铁心磁导很大，所以认为微单元所产生磁势完全作用于窗内圆弧上。即：

则任意电源激励微单元对受影响处所作用的磁密可表示为：

式中，B为矢量磁密；μ0为空气磁导率；By为相间磁场作用的轴向磁密；Bx为相间磁场作用的径向磁密。

从而相间磁场对邻相高低压绕组磁场的影响分析如下。

对于邻相磁场对受影响位置轴向磁密的影响分析为：当忽略距离的影响，则越小受相间磁场影响的轴向磁密越大[6]；当考虑距离时，因为高压绕组距离受影响位置较近，本应只考虑高压绕组对受影响位置磁场分布的影响，但是在绕组端部出现了如图3所示的情况，即虽然高压绕组相对低压绕组距离受相间磁场位置较近，但所作用的电流大小远没有低压绕组大，从而端部所受的轴向磁密影响应主要考虑低压绕组。对绕组轴向中部附近分析时，由于高压绕组整体相对低压绕组距离受相间磁场位置近，所以仅考虑高压绕组对受影响位置相间磁场的影响。由图1和图2可知无论电流微单元水平高度在受影响位置以下还是以上，若电流微单元在高压绕组中，且方向向内，则对受影响区域轴向磁密影响方向为y轴反方向加大，而由低压绕组决定则为y轴正方向加大。

图3中序号1为低压绕组电流面积，序号2为高压绕组面积，由于高低压绕组电流大小相等，所以序号1所指阴影面积电流大小大于序号2所指电流大小。

图3 变压器二维模型

邻相磁场对被影响位置辐向磁密的影响分析为：因为轴向力主要由辐向磁密决定，绕组端部为绕组轴向力最大位置，则仅分析绕组端部辐向磁密受相间磁密的影响[7]。当忽略距离的影响，θ越大受相间磁场影响的辐向磁密越大；当考虑距离时，高压绕组相对较近，且高低压绕组相同比例位置处的电流微单元θ均不小于低压绕组，所以应主要考虑高压绕组对径向磁密，即辐向磁密的影响。假设受影响位置在绕组轴向高度上端，高压绕组电流方向向内，则电流微单元多为在受影响位置下方，即图1中情况，从而得受影响位置辐向磁密为沿x轴正方向加大。若分析受影响区位于绕组下端，则符合图2情况，即受影响位置辐向磁密为沿x轴负方向加大。对于绕组中部上下方向相互抵消，基本不产生相间径向磁场。

图4 常规漏磁分布方向

综上分析，轴向磁密决定辐向力，当邻相绕组电流方向与激励电流微单元所在相电流方向相反时，即同铁窗内绕组截面电流方向如图2所示，则对比常规如图4所示漏磁场方向分布，可知，高低压绕组轴向高度中部辐向力得到增强，而绕组轴向端部轴向力为高压绕组得到增强，低压绕组得到削弱[8]。

采用HPLC-ELSD方法，测定了多批样品中的硫酸盐含量，进而确定了分子式中硫酸的数目，结合样品的酸碱度值，建立了样品酸碱度与硫酸盐含量的关系，对于现行质量标准中的酸碱度是否可以有效控制产品质量开展分析。

2 计算结果分析

本文之前已简要分析相间磁场影响情况，为进一步分析其影响程度，采用三维有限元计算相间磁场。算例变压器三维模型如图5所示。其中油箱设置为隐藏。

在变压器两相短路情况下，以B相绕组为研究对象，分析相间磁场。首先仅对C相绕组添加激励，观察B相绕组截面在图6所示C、B邻相绕组所在铁窗内的轴向和径向磁密分布情况。B相绕组的轴向磁密分布如图7a所示，B相绕组的径向磁密分布如图7b所示[9]。然后对B相绕组也添加电流激励，观察考虑相间磁场时B相磁场变化。

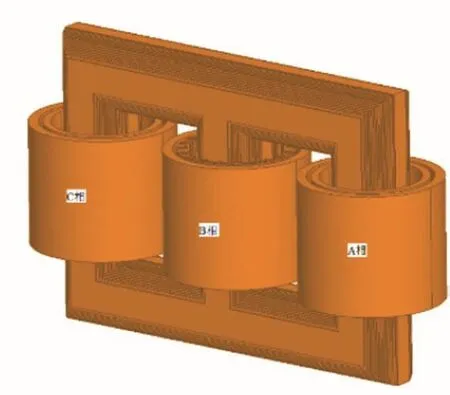
图5 变压器三维模型

图7 仅有相间磁场作用的磁密分布

由图7可知计算结果与分析模型所得结论相同。当B相绕组也添加激励时，得到B、C相低压绕组磁密分布如图8所示。

由图8低压绕组磁密云图可知，邻相相近位置磁密明显大于其他位置，同样验证了相间磁场不可忽略，将变压器B相高压绕组采用饼式结构建立三维模型，对B相高压绕组形变进行分析得到变压器高压绕组端部形变如图9所示，高压绕组中部水平切面形变云图如图10所示。

图8 B、C相低压绕组磁密分布

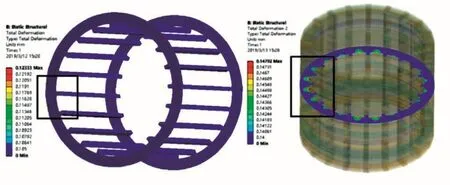
图9 高压绕组端部形变

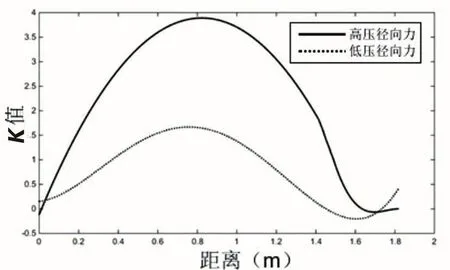
图10 高压绕组中部形变

图9和图10所标注区域为B相绕组与C相绕组相邻位置的形变，同样可见得邻相磁场的影响比较明显。为详细分析相间磁场的影响程度，则对变压器B相绕组建立观测曲线如图11所示。

图11 高压绕组观测曲线

图11为B相高压绕组观测曲线，图中左右半圆周方向均表示为圆弧曲线，分别位于绕组线饼的辐向中心位置，为方便说明，图中指示位置为主空道辐向中心位置，轴向时同样位于各个线饼的高度中心。同时建立相间磁场影响系数，其表示为如下：

式中，F1为B、C相绕组同时添加两相短路电流激励的情况，即为存在相间磁场的情况下对应位置绕组力密度；F0为仅对B相绕组添加两相短路电流激励的情况，即为不存在相间磁场的情况下对应位置绕组力密度；此时采用静态场分析，所添加激励均为最大电流时刻。从而得到高低压绕组端部轴向受力沿观测线K值变化如图12所示，高低压绕组中部辐向受力沿观测线K值变化如图13所示[10]。

图12 轴向受力沿观测线K值变化

图13 辐向受力沿观测线K值变化

由图12和图13可以看出邻相最近位置处高压绕组轴向受力被相间磁场增强15%以上，而低压绕组轴向受力被削弱10%以上；高压绕组辐向力被增强将近4%，低压辐向力增强在1.5%以上。由于相间磁场的影响，很可能出现虽然变压器绕组电流不是最大，而合成漏磁场较大，最终导致非最大电流时刻受力最大，但这种情况只可能发生在最大电流峰值附近。为分析该种情况，以变压器额定运行的高压绕组为例，因为当邻相电流方向与该相方向相反时，相间磁场对高压绕组最大轴向力和辐向力都有增强作用，仍以B相绕组为研究对象，只需在B相电流峰值附近取点即可。

图14 取样时刻

对图14所示电流情况，在t1～t2时刻应主要分析B相绕组中与A相相邻位置。瞬态场计算样点为t1=0.005s到t2=0.05/6s每隔1/6000s（3°）取一个计算样点，各个样点依次命名为样点1，样点2，样点3等等，图14中IA、IB、IC表示为A、B、C三相电流。

从而得到各个时刻高压绕组在图11所示绕组中部和端部的圆弧观测线中心点所在直线上的体积力密度大小。沿该直线各时刻轴向和辐向力密度分别如图15和图16所示。

图15 沿直线各时刻轴向力密度

由图15可见，绕组端部和端部附近最大轴向力密度时刻均不是最大电流时刻，在这种时间样点间隔为3°时并没出现最大辐向力非最大电流时刻，当时间样点间隔为0.3°时出现了这样的情况，如图16所示。

图16 沿直线各时刻辐向力密度

当三相短路时分析相间磁场与额定运行计算方法相同，由图17中局部放大区域可知，当B相电流达到最大时，C相电流更大，但C相电流逐渐减小，导致高压绕组与C相较近位置最大电流时刻仍然为最大受力时刻，但是与A相较近位置仍然会出现以上额定运行时的情况。

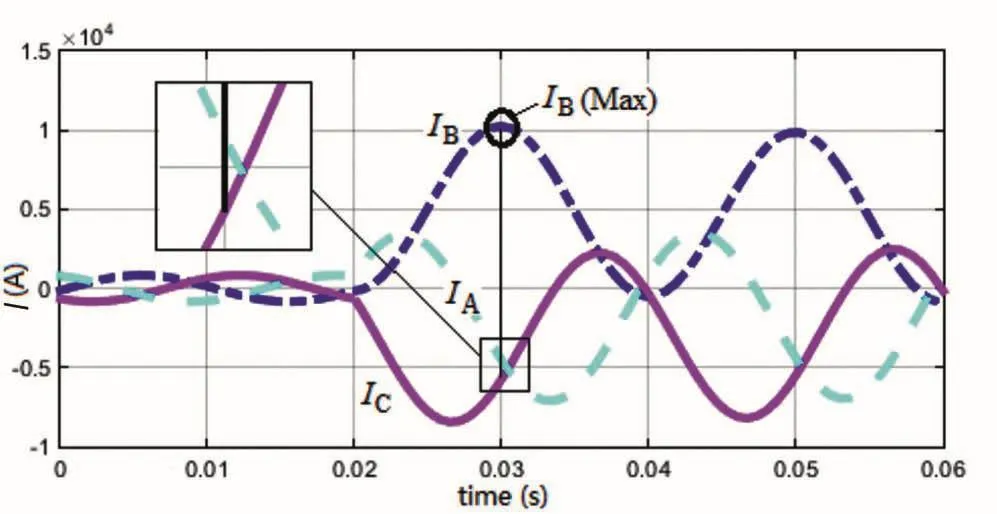
图17 三相短路电流波形

3 结束语

通过对B相绕组进行分析可得到如下结论：

1）在相间磁场影响下，若邻相电流与分析相绕组电流方向相反时，高压端部绕组轴向力和中部绕组辐向力都得到增强，低压绕组端部轴向力得到削弱，而低压绕组中部辐向力得到增强。若电流方向相同，则与该结论相反。

2）当采用两相短路激励分析时，在相间磁场作用下，高压端部绕组轴向力增强15%以上，低压端部绕组轴向力削弱10%以上。高压中部绕组增强将近4%，低压增强1.5%。

3）在额定运行情况下，出现最大受力时刻并非最大电流时刻，而是与最大电流时刻相差一定的电角度，且最大轴向力距离最大电流时刻相差9°左右，而最大辐向力距离最大电流时刻相差不到1°。三相短路时，最大受力时刻为最大电流时刻。