基于相关性分析的3容水箱多参数故障诊断
周 克, 杨小柳, 张发斌, 王 霄
(1.茅台学院酿酒工程自动化系,贵州遵义 564507;2.贵州大学电气工程学院,贵阳 550025;3.重庆樱花能源科技有限公司,重庆 401121)
0 引 言
在工业过程控制中,3容水箱扮演着重要角色。3容水箱可作为许多工业控制对象的典型模型,模拟工业生产过程中的液位、温度和流量等参数变化的控制系统,被广泛应用于控制算法研究中[1-2]。3容水箱系统具有明显的非线性、大惯性和时滞等特性[3],这些特性为各种控制策略的改进提供了研究平台,对控制系统的研究有着重要指导作用。
基于3容水箱,国内外学者在控制算法、系统参数辨识以及故障诊断领域开展了大量研究。刘洪斌[4]将3容水箱建模为一非高斯过程的故障检测问题,利用主成分分析和独立成分分析法对故障进行识别,取得了较好的诊断效果。宋强[5]提出一种新型粒子滤波算法用于故障检测,联合传统粒子滤波算法和遗传算法,解决了传统算法粒子衰退的缺陷,并将算法应用于3容水箱的故障诊断。陈虹丽等[6]将双容水箱建立为T-S模糊模型,通过引入参考模型,建立了故障残差估计误差的广义残差方程,将T-S模型的故障诊断转换为系统鲁棒控制。宋英俊[7]将提升小波控制算法与概率神经网络算法相结合,将小波提升后的数据作为神经网络的输入,经过神经网络的诊断与分析,辨别出系统的故障,并设计故障诊断平台。Mrugalski等[8]针对3容水箱不同执行器出现的故障进行诊断分析,运用神经网络算法对系统进行递归建模,并根据模型设计了可收敛的输入观察器,利用观察器对不同故障产生的结果进行学习,实现了故障类型的诊断以及测试系统对故障的容忍程度。
本文针对3容水箱多个故障同时发生时的问题进行研究,提出一种基于多参数相关性的故障辨别模型,利用智能算法对该模型的各个参数进行了辨识,仿真结果表明,文章提出的方法对于多参数故障辨别,具有较好的应用效果。
1 3容水箱故障建模
3容水箱系统在控制工程中被广泛用于比较和演示,作为实验室过程控制的基准过程[9]。3容水箱结构如图1所示,该模型可以轻易实现多个故障的模拟,如泄漏、堵塞、传感器和执行器等故障。图1中,3个柱形水箱通过连接管两两相连,水箱1、2以及水箱2、3之间的流量受电磁水阀控制,各水箱均连接有泄水阀门,其作用是在必要时排空相应水箱中的液体。水泵1、2用于从回收水箱中将液体抽出,分别流入水箱1、2中,形成闭合回路。

图1 3容水箱系统(电磁,电动)
考虑当水箱间的水阀全部开启以及所有泄水阀门都关闭时,根据物质和能量平衡方程,此时装置的数学模型[10-11]可描述为

式中:S为水箱的横截面积;Sn为排水管道的横截面积;Q1、Q2为分别为水箱1、2的进水流量;hi(t),i=1、2、3分别为每个水箱的水位(cm),可由安装于底部的液位传感器测量;δi,i=1、2、3为介于0到1之间的流量系数;sgn(h)为变量h的符号函数;g为重力加速度。
令X为3容水箱系统的状态向量;U、Y分别为输入向量和输出向量。假设流入水箱的流量Q1=Q2,则有X= [ h1,h2,h3]T∈R3,Y=[h1,h2,h3]∈R3,U=[Q1,Q2]∈R2,Q1=Q2系统在无故障时,其动态模型为
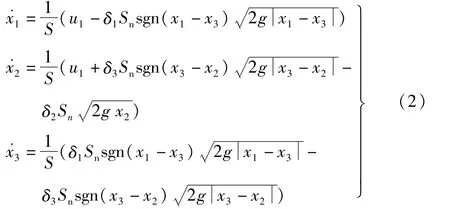
本文主要研究两种典型的非加性故障,即水箱泄漏和管道堵塞故障。
当水箱发生泄露故障时,此时水箱将产生一个新的质量流(cm3/s),令Qfn(n=1,2,3)表示第n号水箱由于泄露而产生的额外流量,其余类推,则各水箱由于泄露产生的质量流可表示为[12]
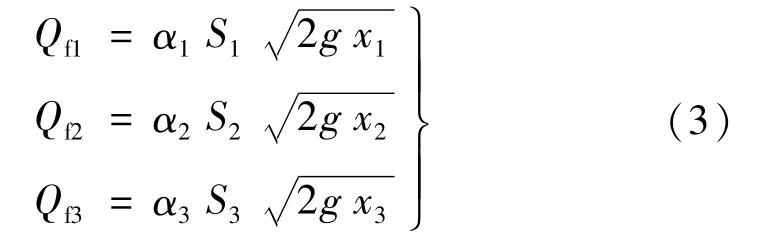
式中,S1、S2、S3分别为水箱漏点的最大横截面。
当水箱间的管道或水箱与回收水箱之间的管道发生堵塞时,由于堵塞引起的质量流可由式(4)表示
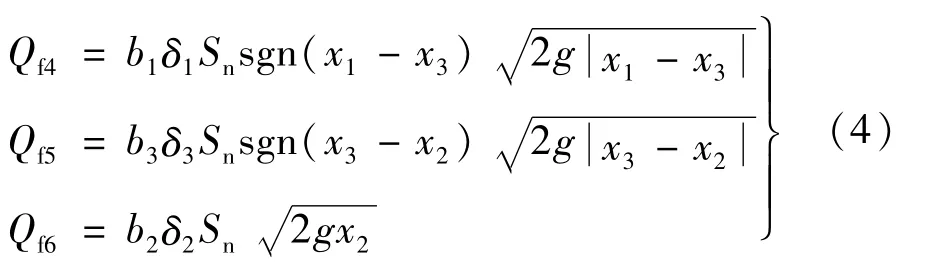
式中,b1、b2、b3∈[0,1]分别为阀门流量系数的比例因子。当上述两种故障同时发生时,此时系统的状态模型:
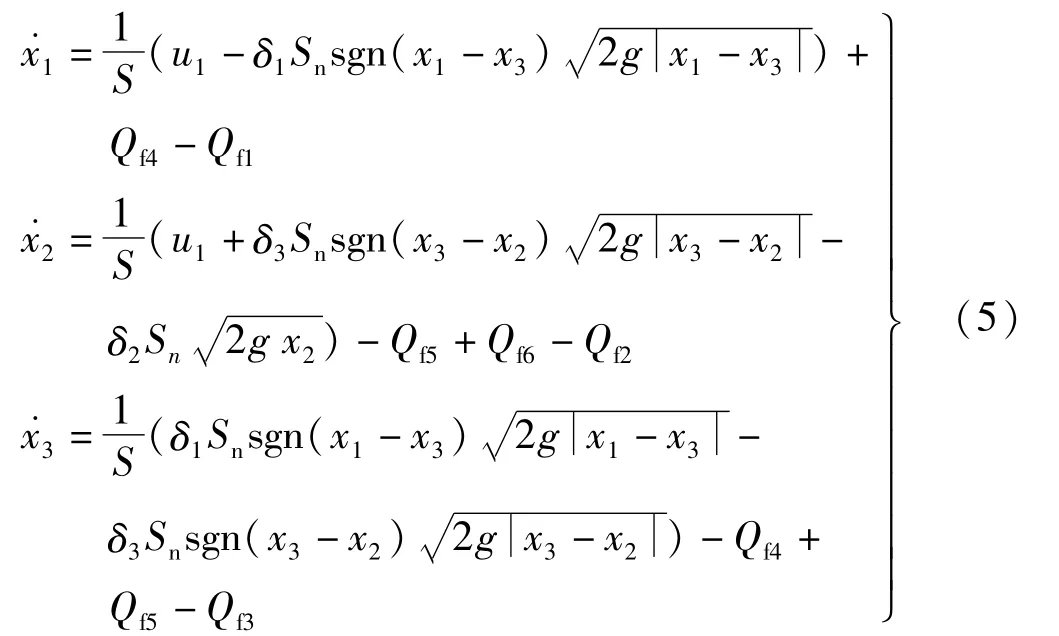
通常情况下,水箱的早期泄漏故障较小,假设水箱漏点的最大横截面积S1、S2、S3与管道的横截面积Sn相等,为了减少公式中的参数,令ρi∈[0,]1表示泄漏点与管道流量系数比例因子,ki∈[0,]1表示泄漏点与管道横截面的比例因子。由此泄漏点处的流量系数和泄漏面积为:

由式(3)、(4)可知,Qf2与Qf6呈现线性相关,故Qf2与Qf6不能同时被诊断。令Q*f2=Qf6-Qf2,则系统的状态方程可改写为:

令各参数的初始值为:θ1=θ2=θ3=0;θ4=θ5=1。不失一般性,此处假设阀门Q20全关闭。式(7)为多元线性回归方程,其矩阵形式为:

式中:


式(9)将3容水箱故障的辨识问题,转化为计算输出向量Y与标称输出二者之间的残差的故障参数辨别的问题。
令R(t)=[r1(t),r2(t),r3(t)]为故障识别系统的输出残差集,使用3个测量信号与标准输出对比,即:

至此,3容水箱的故障问题可以转化为求解系统的输出残差分别与模拟系统和标称系统的残差之间相关系数的优化问题。适应度函数为:

式中,ri、r′i分别为两个系统残差的相关系数。
上述过程对应的系统故障辨识模型如图2所示。

图2 故障诊断模型
2 相关性分析
作为一种统计方法,相关性分析,被广泛用于分析评估两个变量之间关联[13]。利用相关系数法对故障检测模块与故障辨识模块的输出残差进行相关性分析。通过对残差相关系数所构成的适应度函数进行优化,实现故障模拟系统与真实系统输出残差的逼近。当真实系统发生故障时,故障识别系统能够及时识别故障模式和故障参数。
选择皮尔逊相关系数对2个系统的残差输出进行相关性操作,提取故障特征。令向量R、R′分别为式(10)、(11)中定义的残差相关系数:
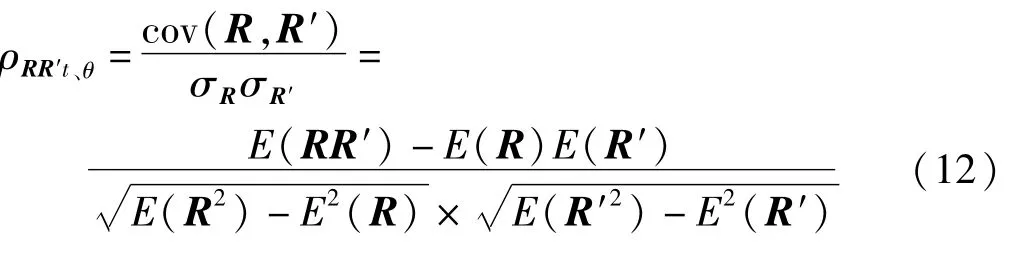
式中:cov为协方差;σ为标准差;E为期望值。皮尔逊相关系数ρRR′在[0,1]范围内变化。上式的使用,需要知道向量R、R′的协方差σR、σ′R。但在实践中,残差系数的这些参数是未知的,很难获得。因此,使用样本相关系数ρXY,替代原来的统计量,其近似表达为:

式中:
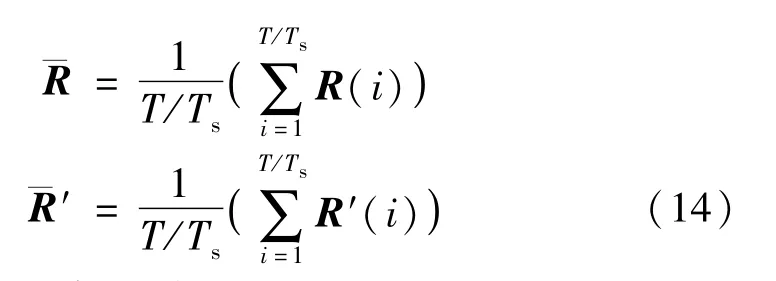
式中:T为用于故障识别的数据窗口的长度;Ts为采样步长;(xi,yi)为样本观测值。越大,说明2个系统的输出残差越接近,模拟系统模拟真实系统变化的效果越好。
3 差分进化算法
由3容水箱的故障模型可知,各个水箱的液位(系统的输出)受到故障参数向量的影响。为寻找系统最优参数,引入DE算法寻求最优解。
差分进化算法(DE)是Storn和Price在1995年提出的一种启发式方法,用于求解多维空间中的全局最优解。DE算法将种群内的最优个体进行记忆并在种群内部进行信息共享,然后依靠变异、交叉以及选择机制在群内产生新的个体。算法主要由种群初始化、变异、交叉和选择4个环节构成。以下为算法的4个步骤。
步骤1初始化。对算法中的迭代次数、变异算子、种群数量以及交叉概率等参数进行初始化,使算法可以按照需要的参数进行迭代。其中,种群的初始化在范围内进行,各种群的初始化设置:

式中:rand(0,1)为均匀分布在区间(0,1)中的随机数,i=1,2,…;NP、NP为种群的数量分别为故障发生程度的最大和最小可能性。
步骤2变异。将种群内任意两个不同个体的差乘以一个大于0小于1的常数,然后与另一个体相加产生新的中间个体。变异的表达式为:
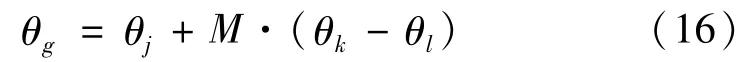
式中:θj、θk、θl为随机选择的种群;θg为变异体;M为收缩因子。
步骤3交叉。按照优化目标将新的中间个体与所选目标个体进行交叉产生候选个体,候选个体与原来的个体进行比较,如果比原先个体性能好,则选择候选个体,否则保留原来的个体。

式中:j=1,2,…,D,D为待辨识参数的维数;jrand为[1,D]之间的随机整数,jrand的引入是为了保证交叉运算至少要从变异体中获得一个元素,保证有新的个体生成,避免无效杂交引发的进化过程的停滞[14];CR为[0,1]之间的数,表示交叉的概率,CR取值越大“发生杂交的可能就越大”。
步骤4选择。将新生个体代入到适应度函数式(11)中进行计算,若该新生个体的适应度比原个体优,则选择新生个体。
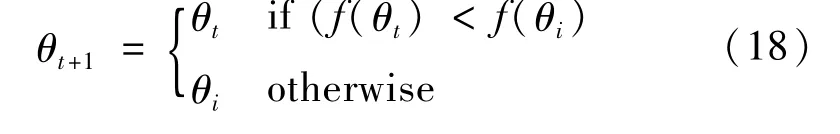
4 实验仿真
为了验证文章所提算法的有效性,以3容水箱为研究对象,研究不同故障条件下,所提模型的有效性,具体实验设置参数如表1所示。

表1 实验参数设置
为验证本文模型的正确性以及对故障参数的敏感程度,在时间为100 s处,分别令故障参数进行微小变化和突变,具体变化见表2。

表2 故障参数变化表
由图3可知,无论是故障参数发生巨大变化或者微小的变化,本文提出的模型均能很好地辨识故障参数的变化,但是,对于故障参数2的参数识别,其误差相对较大,其主要原因是故障参数2与其他故障参数6具有一定的相关性,其准确性受到一定的影响。
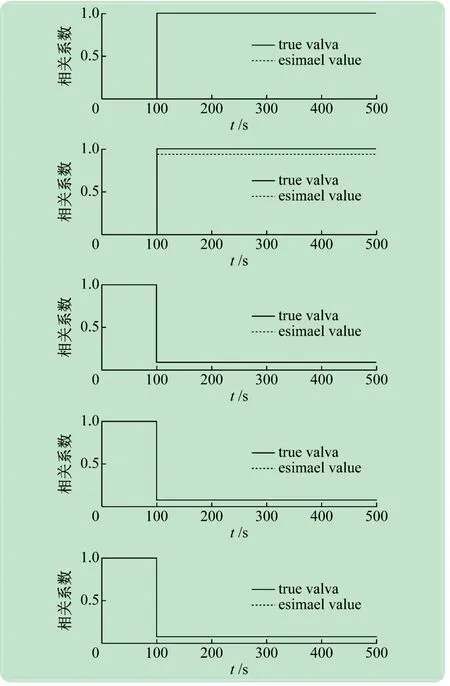
图3 故障参数变化图
图4所示为故障模拟系统与真实系统输出的对比,可见,故障模拟系统的输出与真实系统的输出基本一致,能够及时跟踪真实系统参数的变化。

图4 水箱的实际输出与估计输出对比
仿真实验验证了故障模拟系统对于多参数故障同时发生时,系统对故障参数的辨识效果。辨识结果如表3所示。表3中,每一行为不同故障的故障模式下,系统得到的辨识结果与真实的故障参数的对比。可见,当多故障同时发生时,本文所提的模型依然能够准确地辨识各故障参数的变化。
5 结 语
本文在3容水箱的动态系统基础上,研究系统泄漏和堵塞故障下的微分方程,提出了一种故障参数诊断模型。围绕3容水箱多参数故障的辨识问题,利用相关系数法,对故障检测和故障辨别模块的残差输出进行相关运算,构建了以相关系数为目标的适应度函数。通过引入DE算法对适应度函数进行寻优,实现了故障模拟系统与真实系统参数的一致性。仿真结果表明,本文提出的故障诊断模型和诊断方法,无论是对水箱的单参数故障还是多参数并发故障,均能快速、准确地识别,具有较好的应用价值。

表3 故障参数辨识结果

