基于变色龙算法的共享单车站点聚类研究
管博,江围,周超兰,王庙文,姚杰
(宁波工程学院 电子与信息工程学院,浙江 宁波 315211)
0 引言
随着城市共享单车在全国范围内的不断推广,共享单车乱停乱放现象逐渐成为城市管理的一大难题。城市居民每天的流动规律(工作日早上由居住性质的区域流向商业办公区域,晚上又从商业办公区域流向居住区域)导致共享单车在不同时刻会从某个区域流向另外一个区域,为了解决单车的过度聚集问题,哈罗单车、青桔单车、小溜等多个共享单车运营商都开始通过采取设定禁停区域等一系列措施来限制借车居民对单车的乱停乱放,但效果并不明显。很多学者对共享单车占地聚类进行了研究。例如,陈艳艳等[1]利用K-Means聚类分析算法,呈现北京市7类自行车站点特点,用于运营商或规划人员调整自行车站周边交通布局。董红召等[2]旨在对集合的租赁点进行空间聚类划分,生成调度区域划分方案。周素静等[3]分析了用车高峰时段的借、还车频次,利用spss的交叉联表和K-Means聚类分析法建立聚类分析模型。陆朕等[4]同样采用K-Means的聚类思想,提出了基于自行车使用规模的共享单车租赁点的聚类方法,通过不同天气、季节、日期类型对不同租赁点进行聚类分析,使用特征曲线的描绘,分割、量化分析数据。而城市内共享单车系统就是一个以站点为节点、节点间联系为借还记录的网络拓扑结构。由于共享单车属于短途交通工具,其移动特征应该有明显的城市交通小世界特征,即在某个区域内,大多数共享单车在局部区域内移动,只有少部分单车在区域之间移动。但现有大多研究成果都是基于站点特征进行聚类,忽略了站点之间的联系,无法将城市内共享单车移动的小世界内站点聚成一类。
本文主要是以城市共享单车借还数据为基础,按照城市内共享单车移动的小世界特征,将站点单车的借还次数、借还记录来源站点和借还记录目的站点等作为站点特征,并利用变色龙聚类算法(Chameleon)思想将具有小世界特征区域内的站点作为聚类目标(这些区域内大多共享单车在本区域内移动)。显然,这些大小不同的、具有小世界特征的聚类结果可以用于城市内共享单车调度策略优化、站点选点等相关场景。
1 算法框架
城市内的共享单车运营系统是一个以借还站点为节点,共享单车借还记录为边的图结构。为了更好的描述本算法的实现思想,下面先给出一些基于城市共享单车系统的定义。
定义1(站点的关联集合):给定时间区间t和目标站点si,站点si在时间区间t内的关联集合是在t时间区间内,站点si归还和借走单车的来源站点和目标站点的集合,表示为Rt(si)。
定义2(站点状态):给定时间区间t和目标站点si,时间区间t内站点si的状态是si的所有关联集合中站点sk和关联数nk的组合,如公式1所示。

其中nk其实就是在时间区间t内两个站点之间的单车来往数量之和。
定义3(站点的度):给定时间区间t和目标站点si,该站点的度deg(Si)就是在时间区间内从该站点借走和归还的共享单车数量,即deg(Si)=|St(Si)|
由于共享单车是短途交通工具,大多数单车是在某个局部区域内移动。也就是说,共享单车的移动具有城市小世界特征。如果可以将各个城市小世界内的站点聚成1个子簇,那么这些子簇可以作为当前流行的共享单车调度策略中区域划分的依据。按照变色龙算法的思想,给出子簇相关定义。
定义4(子簇状态):给定时间区间t和由n个站点组成的子簇C={s1,s2,…,sn},那么子簇C在t区间内的状态就是与子簇有关联的子簇以及关联数的集合,如公式2所示。

定义5(子簇的度):给定时间区间t和目标站点si,该子簇的度deg(si)就是在时间区间内从该子簇借走和归还的、不在子簇内站点归还和借走的共享单车数量,即deg(C)=|St(C)|。
定义6(子簇的相对互连性):给定时间区间t和由n个站点组成的子簇C={s1,s2,…,sn},那么2个子簇的相对互联性RI(Ci,Cj)定义如下:

其中|St(Ci)|表示1个子簇Ci做最小截断时需要去掉的边的权重之和,EC(Ci,Cj)表示的是连接2个聚簇的边的权重和。公式(3)表示子簇Ci和子簇Cj之间内部互连性。
定义7(子簇的相对近似性):给定2个子簇Ci、Cj,子簇间相对近似性RC(Ci,Cj)的定义如下:
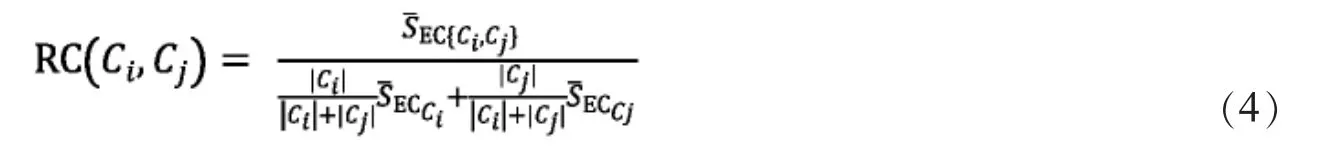
其中|Ci|、|Cj|分别表示Ci,Cj子簇中站点个数,是连接子簇Ci、Cj之间的平均权重,是最小截断时需要去掉的边的平均权重。公式(4)表示子簇Ci和子簇Cj之间内部近似度。
相对互连性描述的是2个子簇的关联程度。其值越大,表示不同子簇之间的站点关联性就越高,相对近似性描述的是2个子簇的相似程度,其值越高,表示2个子簇之间平均关联度与每个子簇内站点间的关联度具有很高的相似性。
按照上述的定义,基于变色龙算法的共享单车站点聚类分析实现框架分成3个步骤:
第一步,按照k-近邻思想将共享单车站点连接图缩减成k-近邻站点连接图,(仅保留每个站点权值大的k条边),最近邻思想的依据不是按照物理位置,而是按照2个站点间共享单车借还的总数(边的权重是2个站点之间的借出和归还数量之和)。
第二步,按照最小边割划分代价思想,将k-近邻图分割成数量众多的子簇,构成初始子簇集。
第三步,按照定义4和定义5计算每2个子簇之间的相对互连性和相对近似性,并将所有子簇对按照子簇相似度公式S=RI(Ci,Cj)+σRC(Ci,Cj)进行排序,合并相似度最大的2个子簇,然后将合并后子簇插入到队列,将相似度最大的子簇进行合并,……,一直到子簇个数达到指定数量。
2 实证分析
为了验证本算法的有效性,本节将对算法生成的站点聚类进行分析和对比。本实验室采用的数据是中国某城市某一年的共享单车借还数据为实验数据,抽取其中的站点借还记录和站点位置为研究数据。由于共享单车站点连接图中站点数量并不庞大,算法第二步中的初始子簇直接是单个站点,σ的取值为1。
图1显示了本算法的聚类结果。从图1可以发现:聚类结果具有明显的小世界特征,整个城市的站点被划分为3个大聚类,聚类1区域内所有站点都是由住在该市老城区居民使用。聚类2区域内的所有站点基本都是在城市在早期扩展区域内居民使用。而聚类4是由该市新城区内居民使用。每个区域都具有一定的封闭性(即小世界特征)。如果在共享单车调度车辆有限情况下,采用局部和全局相结合的调度策略(每个子区域由专门调度车辆负责,区域之间再由全局调度车辆负责)在上下班高峰期要比凭经验调度策略好,因为上下班高峰期间,城市内道路交通拥堵会大大限制车辆的调度速度。
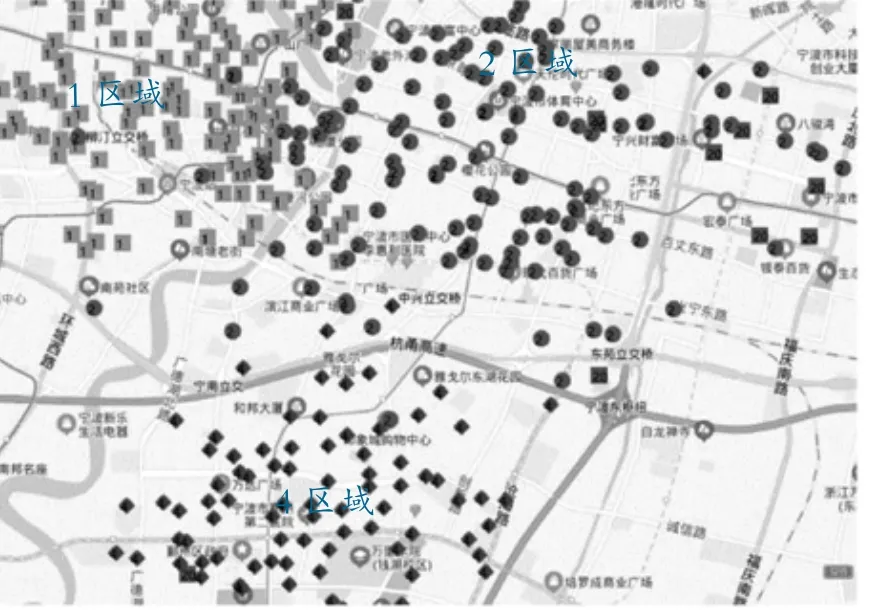
图1 聚类数为20的算法结果
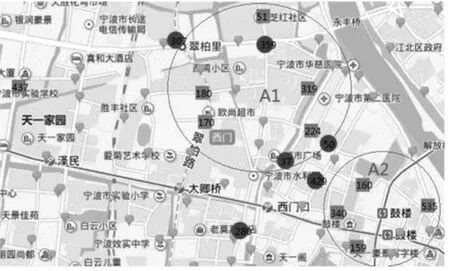
图2 聚类数为50的部分聚类结果图
图2显示了当聚类数为50的部分聚类结果图。从图中可以发现:同一个聚类的6个圆形站点从位置上来看并不封闭,西北方的2个站点与东南方的4个站点并不相邻,中间还隔着4个站点。但从城市功能区角度来看,该聚类处在居住区A1的周边,同样具有一定的封闭性(小世界特征)。
综上所述,算法不仅可以将共享单车移动相对独立的区域找出来。而且,随着预设聚类个数的变大,原来的聚类逐渐变成多个小区域的聚类。显然,这些小聚类展示着具有局部独立性的小区域。这些聚类结果可以解决当前共享单车调度策略中区域划分困难的窘境,以这个聚类为依据对调度车辆进行调度,针对每个区域的共享单车移动特点,配置不同数量的调度车辆,只要保证区域内移动共享单车的循环闭环,那么该区域的共享单车就不会存在单车过度聚集问题。
3 结语
基于变色龙算法的共享单车站点聚类算法可以很好地挖掘城市中共享单车移动的小世界区域,使得共享单车调度可以按照这些小世界区域进行车辆调度区域的划分,方便实现小世界区域内移动共享单车的循环闭环,减少单车过度聚集,缓解调度压力,提高共享单车调度效率。

