海洋非粘结柔性管道骨架层刚度有限元分析

崔 巍，张煜杭，张 强

(东北石油大学 机械科学与工程学院，黑龙江大庆 163318)

0 引言

海洋非粘结柔性管道是我国海洋油气资源开采的重要装备之一，其结构如图1所示。随着陆地油气资源逐年减少，我国开始加大对海洋油气资源的开发利用[1]，对海洋柔性管道的使用率也逐年提高[2-3]。与传统的单层钢管相比，非粘结柔性管道由于具有较好的柔性，在实际应用中能够更好地承受由于洋流与浮式生产设备运动等因素产生的变形，更能适应恶劣的海洋环境[4]。此外，非粘结管道还具有耐腐性能好、便于模块化设计、易于铺设和回收等优点[5]。

图1 海洋非粘结柔性管道示意 Fig.1 Schematic diagram of structure of unbonded flexible pipe

在非粘结柔性管中，骨架层的主要作用是提供径向上的刚度和强度，以承受管道的外部压力，避免因外部压力过大导致压溃现象的发生[6]。此外，由于海洋柔性管道在实际工况中还会承受拉压、扭转和弯曲等载荷，同样有必要研究骨架层对于这些载荷的响应情况。

目前，关于各种油气管道力学性能的研究十分丰富[7-9]，而针对非粘结柔性管道的局部力学性能研究还不够完善。在已有的非粘结柔性管道的有限元分析中，一般都是将骨架层等效为一定厚度的均质圆筒或各向异性壳进行建模[10-11]，或者提出一种双材料有限元模型代替复杂的螺旋结构[12]，这些等效模型的刚度值往往与真实情况存在偏差。此外，部分研究忽略了骨架层轴向拉压时的自锁和钢带之间的摩擦条件[13-14]，导致分析结果更加不准确。

由于骨架层钢带间存在接触、摩擦等非线性因素，即使在材料弹性变形范围内，骨架层的拉压弯扭等变形与载荷之间仍存在非线性特性。为了更加准确地分析海洋非粘结柔性管道骨架层的刚度，采用ANSYS数值分析方法，考虑了骨架层钢带之间的摩擦和自锁，建立了骨架层的三维有限元模型，弥补了以往简化模型的不足。本文计算了骨架层在拉伸、压缩、扭转、弯曲及外压载荷下的变形，分析了骨架层在各种载荷下的“载荷-应变”曲线以及相应的刚度和应力。

1 有限元模型

1.1 骨架层结构

骨架层管道采用了互锁结构与螺旋缠绕结构相结合的设计方法，由横截面近似为S形的钢带绕管体中轴螺旋缠绕互锁而成。本文参考WITZ[15]案例研究中的尺寸，创建了非粘结柔性管的骨架层三维有限元模型，其钢带的S形横截面形状尺寸如图2所示。

钢带材料为304不锈钢。骨架层管道内径为63.2 mm，壁厚3.5 mm。钢带的S形横截面由28 mm×0.7 mm的矩形经多次冷弯制成，截面高度为15 mm，横截面积为19.6 mm2。钢带以左手螺旋的方式沿轴线缠绕形成管体。螺旋角即缠绕方向与中轴线夹角为87.5°，根据公式(1)得出此时钢带的螺距为8.668 8 mm。

(1)

式中，θ为螺纹升角，(°);n为螺纹线数(此处取1);p0为初始螺距，mm;D为骨架层内直径,mm。

1.2 网格与边界条件

本文建立了骨架层4圈和5圈的钢带模型。其中，4圈钢带模型用于拉伸、压缩、扭转及外压分析，5圈钢带模型用于弯曲分析。为了便于施加约束与载荷，本文将骨架层模型两端补平。由于两端补平结构在实际骨架层管道中并不存在，在提取分析结果时，不考虑补平结构本身以及与两端补平相连接的两圈骨架层的分析结果。根据圣维南原理，两端约束和载荷的施加方式对于距离模型两端较远的中间部分钢带的分析结果没有影响。因此，对于4圈钢带模型来说，中间2圈钢带的分析结果有参考意义。同理，对于5圈钢带模型来说，中间3圈钢带的分析结果有参考意义。采用Solid 186单元进行网格划分，弹性模量为199 GPa[12]，泊松比为0.3，材料屈服极限为205 MPa。划分好的有限元网格如图3所示。

图3 骨架层有限元网格 Fig.3 FE mesh details of the carcass model

此外，为钢带之间产生接触的表面添加接触设置，采用的接触单元和目标单元分别是Conta 174和Targe 170。根据机械设计手册，摩擦系数取为0.15[16]。接触单元与目标单元设置如图4所示。

图4 添加接触面示意 Fig.4 Schematic diagram of contact regions of the carcass layer model

在拉压、扭转与弯曲分析中，将图3的补平管道模型下端面节点，设置为全约束；在模型上端面中心处，建立导航节点，并使其与模型上端面节点绑定；最后，在导航节点处分别施加拉伸、压缩扭转和弯曲载荷。在外压分析中，将4圈钢带模型两端端面施加全约束，模型外壁施加均匀外压。

2 结果分析

2.1 拉伸、压缩分析

骨架层具有互锁的结构特点。在初始状态下，相邻圈数的钢带在轴向上留有一定空隙[17]，如图5(a)所示，其中，p0为骨架层的初始螺距8.668 8 mm，但当骨架层被拉伸或压缩时，钢带发生滑动并自锁；图5(b)是骨架层轴向受拉时的自锁状态，其中，钢带横截面j点与相邻钢带bc段接触，a点与hi段接触，钢带横截面各段标号如图2所示，此时螺距p1=8.844 9 mm；图5(c)是骨架层轴向受压时的自锁状态，钢带横截面ef段分别于上下相邻钢带的bc段和hi段之间发生接触，此时螺距p2=7.796 0 mm。骨架层在初始状态下的拉伸和压缩刚度极小，可忽略不计。当骨架层轴向受拉或受压并自锁时，其拉伸或压缩刚度骤增。本文研究产生自锁现象下的拉伸与压缩刚度。

(a)初始状态

在拉伸、压缩分析中，选择4圈钢带模型施加载荷。在分析结果时，则选择模型最中间的1圈钢带，即第2圈后半圈与第3圈前半圈组成的一整圈钢带。为了提取骨架层的拉伸和压缩应变，取模型最中间1圈钢带两端的S形横截面相同位置的两个节点，如图6所示，这两个节点的距离刚好等于骨架层钢带的1个螺距。提取这两个节点的轴向位移，两个节点的位移差即为1个螺距长度的骨架层在拉伸或压缩状态下拉伸量或压缩量。拉伸量或压缩量除以1个螺距长度的结果，即为骨架层的拉伸应变或压缩应变。

图6 选择用于度量应变的节点示意 Fig.6 Schematic diagram of nodes for measuring strain

图7示出了骨架层在材料弹性范围内的拉压载荷与应变的关系曲线，曲线的斜率即为拉伸、压缩刚度。

图7 拉伸、压缩分析的载荷-应变关系曲线 Fig.7 “Load-strain” curve for tension and compression analysis

从图7可以看出，骨架层管道自锁导致轴向具备一定的拉压刚度，因此以往研究[13-14]中忽略管道自锁的简化模型是不准确的。在拉伸状态下，随着载荷的增加，曲线斜率最初呈缓慢增长趋势；当拉伸载荷达到约800 N时，曲线斜率保持基本不变。在压缩状态下，曲线斜率随载荷增大保持基本不变，且曲线斜率明显大于拉伸分析的曲线斜率。因此，管道的压缩刚度明显大于拉伸刚度。

图8示出了骨架层最中间1圈模型在受拉压时的应力分布。在图8(a)中，当骨架层模型施加2 200 N轴向拉伸力时，最大节点应力为192.1 MPa，钢带横截面gf段存在应力集中，同时为最大应力所在处;在图8(b)中，当骨架层模型施加5 600 N轴向压缩力时，最大节点应力为198.6 MPa，最大应力所在处同样存在于钢带横截面gf段。此时，横截面gf段的应力接近材料的屈服极限205 MPa，为避免骨架层产生塑性变形，使其对载荷有更好的承载能力，有必要优化这部分的结构尺寸。

(a) 施加2 200 N拉伸力 (b) 施加5 600 N压缩力

骨架层钢带横截面的gf段和de段均为钢带冷弯加工时弯折的部位。如图2所示，这两处的弯折角度α均为75°，圆角半径r均为1 mm。由于gf段是拉压分析中的最大应力处，通过分别修改参数α和r，研究弯折角度和圆角对gf段应力集中的影响。

表1示出骨架层在受拉、压状态下，不同截面尺寸gf段的应力。可看出，当r一定时，gf段应力随α增大而增大；当α一定时，gf段应力随r增大而减小。其中，r=1.2 mm，α=70°时结构尺寸最为合理，此时拉伸状态下的gf段应力下降至180.6 MPa，压缩状态下的gf段应力下降至177.3 MPa。

表1 不同尺寸gf段的应力数值

2.2 扭转分析

在扭转分析中，选择4圈钢带模型进行分析。选择分析顺、逆时针扭转两种情况。其中，顺时针扭转为顺着钢带缠绕的方向施加扭矩，逆时针扭转则反之。

在提取骨架层管道单位长度的扭转角时，选择节点的方式与拉压分析中的方法相同，仍是选择骨架层最中间1圈钢带两端S形横截面相同位置的两个节点(如图6所示)。分别提取这两个节点的初始坐标和施加载荷后的坐标，就能计算出每个节点绕模型中轴旋转的角度。两个节点的旋转角度之差即为一个螺距长度的骨架层管道的扭转角，再除以1个螺距长度就得出单位长度的骨架层管道的扭转角，即模型的扭转应变。

骨架层材料弹性范围内顺、逆时针扭转分析的载荷-应变关系曲线如图9所示，曲线的斜率即为骨架层管道的扭转刚度。骨架层管道顺时针和逆时针扭转刚度都随载荷的增大而增大，且顺时针扭转刚度始终略大于逆指针扭转刚度。

图9 顺、逆时针扭转分析的载荷-应变关系曲线 Fig.9 “Load-strain” curve for clockwise and counter-clockwise torsion analysis

骨架层模型最中间1圈钢带应力云图如图10所示。在图10(a)中，当骨架层模型顺时针施加20 N·m扭矩时，最大节点应力为127.4 MPa，最大应力处在钢带横截面ab段；在图10(b)中，当骨架层模型逆时针施加20 N·m扭矩时，最大节点应力为197.3 MPa，最大应力处在钢带横截面ij段。

(a) 顺时针施加20 N·m扭矩 (b) 逆时针施加20 N·m扭矩

图11示出了扭转状态下骨架层钢带局部位移云图。

图11 扭转状态下钢带局部位移云图 Fig.11 Local displacement nephogram of steel strips under torsional load

可以看出，扭矩引发了钢带间的滑动与接触。在图11(a)中，模型受顺时针扭矩作用时，钢带横截面ab段与相邻钢带横截面gh段发生接触；在图11(b)中，模型受逆时针扭矩时，钢带横截面ij段与相邻钢带横截面cd段发生接触。骨架层钢带间主要依靠接触传递变形和应力，而在顺、逆时针扭矩下ab段和ij段分别产生较大接触变形，因此为最大应力所在位置。

2.3 弯曲分析

在弯曲分析中，由于至少需要3圈钢带的分析结果才能度量弯曲变形，因此选择5圈钢带模型进行分析。为提取弯曲应变，需要分析骨架层管道受压一侧的压缩量和受拉一侧的拉伸量。因此，本文在管道的压缩侧和拉伸侧分别选择3个节点。图12为骨架层模型中间3圈钢带沿XY面切割的剖视图，所选择节点位置如图所示。

图12 选择用于度量弯曲变形的节点示意 Fig.12 Schematic diagram of nodes for measuring bending deformation

以压缩侧为例，所选择的3个节点与管道中轴的距离相等，且在XY面上，每相邻的2个节点的距离为1个螺距。提取压缩侧所选择的节点在变形后的坐标，计算出在弯曲状态下3个节点相连形成的圆弧的弧长，用2个螺距减去弧长得到2个螺距长度的骨架层压缩侧的压缩量，用所得的压缩量除以2个螺距，即为骨架层压缩侧的压缩应变。同理，可以计算出骨架层拉伸侧的拉伸应变。骨架层管道的弯曲变形示意图如图13所示，根据公式：

εt=y1/ρ

(2)

εc=y2/ρ

(3)

D=y1+y2

(4)

可以得出：

ρ=D/(εt+εc)

(5)

式中，εt为拉伸侧的拉伸应变；y1为拉伸侧所选择用于度量应变的节点距离管道弯曲中性层的距离，mm；ρ为曲率半径，mm，其倒数为单位长度骨架层的转角，即骨架层的弯曲应变；εc为压缩侧的压缩应变；y2为压缩侧所选择节点距离管道弯曲中性层的距离，mm；D为所选节点与管道中轴距离的2倍，mm。

图13 骨架层弯曲示意 Fig.13 Schematic diagram of bending condition of the carcass layer

图14示出了骨架层在材料弹性范围内弯曲分析的载荷-应变关系曲线。其中，曲线的斜率即为骨架层管道的弯曲刚度。可以看出，曲线斜率随着载荷增大呈现略微上涨趋势，但增长幅度不大。因此，随着弯矩的增大，骨架层的弯曲刚度近似不变。

图14 弯曲分析的载荷-应变关系曲线 Fig.14 “Load-strain” curve for bending analysis

骨架层模型施加20 N·m弯矩的状态下，模型中间部分钢带的应力云图如图15所示，钢带局部变形情况如图16所示。

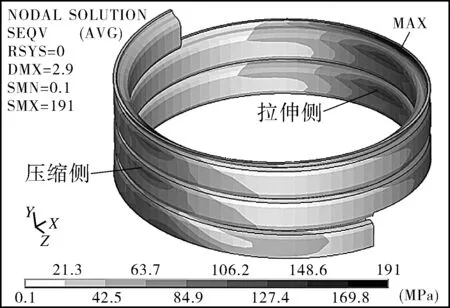
图15 施加20 N·m弯矩时的应力云图 Fig.15 Stress nephogram of the model under bending load of 20 N·m

图16 施加20 N·m弯矩时的局部位移云图 Fig.16 Displacement nephogram of the model under bending load of 20 N·m

骨架层管道在弯曲状态下，弯曲中性层两侧中的一侧受拉而另一侧受压。从图15中可以看出，受拉、压两侧应力较大，而弯曲中性层附近部分的应力则几乎为零。其中，管道压缩侧钢带的横截面ef段存在较大应力，原因是受到相邻钢带bc段和hi段的挤压；拉伸侧钢带横截面的de段和gf段也存在较大应力；拉伸侧gf段为弯曲状态下最大应力所在处。

表2示出了在弯曲状态下，弯折角度α和圆角半径r对拉伸侧gf段应力的影响。通过表2可以看出，当r一定时，拉伸侧gf段应力随α增大而增大；当α一定时，应力随r增大而减小。其中，r=1.2 mm，α=70°时结构尺寸最为合理，此时gf段应力下降至167.5 MPa。

表2 不同尺寸拉伸侧gf段的应力数值

2.4 外压分析

非粘结柔性管道在海洋环境中主要受到外压的影响。在非粘结柔性管的实际结构中，由于骨架层外部与防渗漏层相邻，且防渗漏层内壁与骨骨架层的外壁，即钢带gh段外表面相接触。当外压传递到骨架层时，钢带gh段外表面承受外压。故选择骨架层4圈钢带模型，上下两端面节点施加全约束，并在gh段外表面施加均匀外压。

提取骨架层管道在外压作用下的径向位移，在4圈钢带模型最中间1圈钢带上，选择如图17所示的2个节点，分别提取这2个节点沿管道径向位移。

图17 外压分析节点选择示意 Fig.17 Schematic diagram of nodes for measuring radial displacement

施加外压与节点径向位移的变化曲线如图18所示。在材料弹性范围内，外压并未导致钢带之间发生明显的接触，径向位移随外压的增大近似为线性增长，骨架层钢带上不同点的径向位移基本一致。

图18 外压分析的外压-径向位移关系曲线 Fig.18 “Load-radial displacement” curve for external pressure analysis

3 结论

本文采用ANSYS有限元分析软件，建立骨架层管道的三维有限元模型，考虑钢带之间的摩擦和接触因素，分析了骨架层在受到拉伸、压缩、扭转、弯曲以及外压时的变形，得出骨架层材料弹性变形范围内，各种载荷下的载荷-应变关系曲线，得出以下结论。

(1)随着拉伸载荷的增大，骨架层管道的拉伸刚度先略微增大，后保持基本不变。压缩刚度随载荷的增大保持基本不变，且管道的压缩刚度明显大于拉伸刚度。

(2)骨架层管道的顺时针扭转刚度略大于逆指针扭转刚度，且都随载荷的增大而增大。

(3)骨架层管道的弯曲刚度随着载荷的增大保持基本不变。

(4)随着外压增大，骨架层管道径向位移呈近似线性增长趋势。

此外，本文研究了关键尺寸对骨架层结构应力集中的影响，通过优化尺寸有效减少了骨架层的应力集中。