一种基于加权最小二乘载频估计的单星定位算法①
朱重儒,朱立东
(电子科技大学通信抗干扰技术国家级重点实验室,成都 611731)
0 引言
无源卫星定位技术具有定位范围广、侦查方式隐蔽以及易于实现等特点,在民用和军事领域都发挥着极大的作用[1-2]。对于低轨道卫星定位,多星座体制定位依赖于多颗卫星协同定位,可采集更多辐射源信息,定位精度有所提升,但与此同时,多星座体制的时差定位对星间时钟同步要求严格,时差信息对定位精度影响较大,给实际定位应用增加了难度,单颗卫星相对多星座体制,成本低廉,定位原理简单,避开了复杂多变的组网设计,且多普勒信息容易得到,因此单星定位技术仍有较好的发展前景[3]。
对于来自地面的未知载频信号,需要进行载频估计,目前常用的载频估计方法主要是硬件法和软件法[4]。硬件法方面,不同的工程项目会设计出不同电路图,硬件法适用性差且成本高昂,不适合用于定位系统中的载频估计环节。对于软件法,算法设计更加灵活方便,常见的算法有傅里叶算法、线性预测法、最小二乘法、Chirp-Z变换法等。傅里叶算法频率估计精度低,且傅里叶变换计算量大,线性预测法更适合具有线性关系的参数估计模型[5],最小二乘法初值的选择具有任意性,载频估计结果受初值选取的影响较大[6],Chirp-Z变换法要求确定待估计频率的范围,以对频谱进行细化。受计算复杂度和测频精度的相互制约,卫星对地面辐射源进行精确实时的定位得不到保证,如何平衡计算复杂度和测频精度,是单星定位中亟需解决的问题。
在单星定位实现过程中,需要采集卫星不同时刻的星历信息和接收机信号的参数,数据量大。针对最小二乘载频估计法具有计算复杂度低、测频精度不高的特点,本文提出一种基于加权最小二乘载频估计的单星定位算法,在保证较小计算复杂度的同时,提高测频精度,使得定位点更加靠近真实的位置。另外,本文分别研究了通信信号载频、卫星接收信号时长两方面对单星定位结果的影响,选择合适的信号载频和接收信号时长,可提高定位精度。
1 单星定位原理
通常通信信号和雷达信号均被认为是窄带信号,本文假设地面辐射源的发射信号和卫星接收机接收信号均为如式(1)所示的窄带信号[7]:
s(t)=A(t)·exp(j·2πf0t)
(1)
其中,f0是发射机信号的载频,A(t)为发射信号的包络。对于窄带信号的传输,可以知道,当卫星处于运动状态时,接收机的接收信号会受到多普勒效应的影响,接收信号的载频等于发射信号的载频叠加多普勒频率,由信号模型可知,接收信号的瞬时频率为:
f=f0+fd
(2)
其中,fd表示多普勒频率,且多普勒频率与卫星和辐射源的径向速度满足式(3)的关系式,c表示电磁波传输速度,大小为2997 924 58 m/s。
(3)
r′(t)是卫星和目标辐射源之间径向距离的导数,即二者的径向速度的大小。径向速度又可以用相对位置矢量和相对速度矢量表示,如式(4)所示[8]:
(4)
其中,T表示矢量的转置,v是卫星与目标之间的相对速度矢量,r是卫星与目标之间的相对位置矢量,|r|是卫星与目标之间的距离大小。将式(3)和式(4)代入式(2),则信号频率可表示为:
(5)
根据单星无源定位的运动模型,在第i个时刻观测到的多普勒频率可表示为[9]
(6)
其中,ζi是第i个时刻的测频误差,是服从独立高斯分布的白噪声成分,Fi(x,y,z),可视为低轨卫星与辐射源在相对运动过程中的多普勒效应。当卫星过境辐射源上空时,可在N个时刻接收到辐射源的信号,N个时刻的载频测量值用矩阵形式表示如式(7)所示:
φ=f0·F+ζ
(7)
其中,φ代表N个时刻卫星接收机接收到的信号频率的矢量,F是可以表征多普勒效应的矢量,ζ表示信号接收时受到的干扰噪声。在式(7)中,只有信号载频f0是未知,由载频估计方法计算得到fk,l,建立如式(8)的代价函数模型[10]:
J(Lk,Bi)=‖φ-fk,l·F‖2
(8)
选择使得式(8)最小的(Lk,Bl)作为辐射源位置的解算结果,本文仿真将式(8)的代价函数取倒数,数据显示更加直观。
2 加权最小二乘估计原理
最小二乘法的核心思想是通过已有数据建立自变量和因变量之间的最佳对应关系,在建立关系的过程中优化模型参数。对于确定的目标函数模型,自变量和因变量是已知的变量,系数或者常量是带估计的参数,根据最小二乘计算公式建立目标函数模型,进行加权处理并计算估计值[11]。由式(6)和式(7)可构建系统模型为:
Y=f0·X+ζ
(9)
其中,Y为模型的输出,即卫星接收信号载频φ,X为模型的输入,即X=F(x,y,z),包含卫星星历等信息,ζ为高斯白噪声,即接收信号载频误差,f0即为本文估计的辐射源发射信号载频,根据最小二乘法理论,可得到f0粗略的估计值为:
f′=(XTX)-1XTY
(10)
估计得到的参数f′再代入模型中得到的输出为Y′,估计系统输出Y′与实际输出Y存在误差e,也可以被称为残差,残差的表达式表示为:
e=Y-Y′=Y-f′X
(11)
随机噪声误差项的方差ζ与系统输入的解释变量X存在相关性,上面的最小二乘模型存在异方差,为了使得f′为无偏估计值,通过残差e构造误差权重矩阵W。
(12)
其中,权重函数为wi=tanh(e)/e, 则新的加权最小二乘参数估计可表示为[1]:
f′=(XTWX)-1XTWY
(13)
3 基于加权最小二乘载频估计的单星定位算法
采用通常使用的WGS-84地球模型,对于地球表面的目标辐射源而言,至少需要两个定位曲面就可以确定其位置坐标。当卫星观测了足够次数的信号频率后,在星下足够大的区域内以经纬度进行网格划分,定义二维网格点集∑。令k,l分别表示网格的纵横计数,对每个网格点(Lk,Bl)∑,结合星历信息中的卫星位置坐标、卫星速度和加速度以及卫星接收机接收到的信号频率,由式(7)和式(14)计算f0的加权最小二乘解为:
fk,l=(FTWF)-1FTWφ
(14)
对每一个求得的载频计算式(15)代价函数,选择使得最小的(Lk,Bl)作为辐射源位置的最优估计。
J(Lk,Bl)=‖φ-fk,l·F‖2
(15)
基于加权最小二乘载频估计的单星定位算法的具体步骤如表1所示。

表1 单星定位算法步骤
4 实验仿真
设置地面站辐射源经纬度坐标为(118.5°,22.5°),发射信号频率为1.3 GHz。卫星上的接收机只能在地面站辐射源的过境区域接收到信号,于是在表示接收机信号频率的星历中找到与估计载频最接近的时刻,以这个时刻为中心,在前29 s和后30 s时间段内,取对应的卫星位置、速度、加速度以及接收机接收频率作为采样数据,且对这60 s的接收信号频率叠加服从高斯分布的测频噪声。根据表1中的步骤进行仿真。
在STK软件中,设置好卫星运动场景,分别导出卫星围绕地球一周的坐标、速度和加速度,以及卫星接收机上的接收信号频率。发送信号和接收信号频率如图1所示,当卫星与地面站发生相对运动时,接收频率的大小发生变化。查文献[12]可知,对于1.3 GHz信号频率稳定度是10-8,误差在十几赫兹量级,于是在接收端叠加均值为0,方差为15 Hz的正态随机噪声[12]。显然,在取得的60 s时间内,卫星经历了靠近地面站再远离地面站的过程。
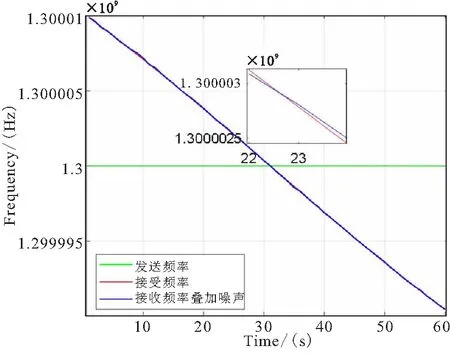
图1 发送信号和接收信号频率
通过卫星的坐标求出该时间段的星下点轨迹,找到星下点轨迹的中心点,经纬度变化幅度为±5°,确定第一次网格搜索的经纬度范围,经度范围为[112.6169 122.6169],纬度范围为[17.7030 27.7030],网格大小为0.1*0.1,第一次搜索得到两个定位结果,再分别对两个定位结果的领域进行精搜索,经纬度变化幅度为±0.1,网格大小为0.01*0.01。在每一个网格点对信号载频进行估计。前面已经得知,载频估计的精度影响着辐射源估计的精度,最小二乘法估计得到的信号载频没有加权最小二乘法估计得到的载频精确,二者载频估计的误差如图2所示,本文提出的方法载频估计误差保持在-60 Hz到60 Hz之间,而最小二乘法估计的载频误差在-160 Hz到220 Hz之间,与前面的结论一致。

图2 载频估计误差
定位结果如图3所示,黑色的虚线表示卫星在60 s内的星下点轨迹,蓝色三角表示地面站辐射源实际坐标,其余6个点表示定位结果坐标,其中3个是第一次网格寻优时的定位结果,另外3个是第二次网格寻优定位结果,根据先验信息,舍弃模糊值。由仿真显示,对于实际辐射源经纬度坐标(118.5°,22.5°),定位结果坐标为(118.4915°,22.4826°),定位误差为2.449 km。

图3 定位仿真结果
第一次网格寻优时,每个网格点对应1-8式中代价函数的值如图4所示。由卫星运动场景知道,星下点轨迹确定的网格坐标,在定位中总会存在着两个对称的点使得代价函数的值达到最大(最小),最优值对应的经纬度即为定位点。

图4 粗搜索代价函数仿真结果
由第一次代价函数寻优得到的三个定位点经纬度坐标分别是[118.4896°,22.5255°]、[117.8896°,22.4255°]、[118.5896°,22.5255°],分别在其邻域进行第二次代价函数寻优的仿真结果如图5所示,(a),(b),(c)分别代表第二次网格搜索后代价函数的三维图,第二次代价函数寻优得到的三个定位点经纬度坐标分别是[118.4972°,22.5013°]、[118.4968°,22.4862°]、[118.5014°,22.5130°],比第一次搜索的定位结果更加准确。

图5 精搜索代价函数仿真结果
5 定位精度影响因素分析
5.1 信号载频对定位精度的影响
为研究辐射源信号载频对定位精度的影响,现设置辐射源位置,卫星轨道高度等参数不变,分别设定信号载频为1.3、2.6、3.4(单位:GHz),其多普勒频率和多普勒频率变化率如图6所示。
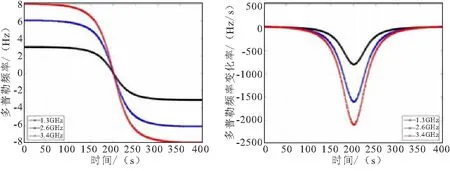
图6 多普勒频率及其变化率
用相同的网格寻优对辐射源进行定位,且在同一信号载频时,解算时设置载频均方误差分别为10 Hz、30 Hz、60 Hz、120 Hz、180 Hz、240 Hz、360 Hz、480 Hz,定位结果如图7所示。

图7 信号载频对定位结果的影响
通过图6可以发现当信号载频越小时,卫星与地面站的相对运动速度减小,多普勒频率效应减弱,且多普勒频率变化率减小。通过图7可以发现信号载频越小,定位误差越大。
5.2 接收信号时长对定位精度的影响
为研究信号时长对定位精度的影响,现设置辐射源位置,卫星轨道高度等参数不变,分别设定信号时长为20、40、60、80(单位:s),该时长指以星下点轨迹中心为对称的时间范围。不同信号时长对应的定位误差如图8所示。

图8 接收信号时长对定位结果的影响
通过图8可以发现当信号时长越长,定位误差越小;相反,若信号时长越短,定位误差越大。由于信号时长越长,接收机能够获得频率信息越多,最小二乘法估计的载频更加准确,因此能够提高定位精度。
6 结束语
本文将辐射源定位问题转化为发射信号载频估计问题,提出一种基于加权最小二乘载频估计的单星定位算法,通过理论推导和仿真验证,可以发现加权最小二乘法估计得到的载频精度更高,从而辐射源实际的坐标漂移更小,定位误差更小。此外也分析了信号载频、信号时长等因素对定位结果的影响,发现轨道倾角对定位结果影响较小,轨道高度越低,发射信号载频越大,接收信号时长越长,定位精度都有一定程度的提高,为低轨卫星的轨道设计和后续算法改进提供了新的思路。

