潜水器用光纤线团应力分布及影响因素
汤伟江,刘卫东,高卓,张凯,赵培东
(1.西北工业大学 航海学院,陕西 西安 710072;2.中国船舶集团有限公司 第705研究所,陕西 西安 710077;3.西北工业大学 水下信息与控制重点实验室,陕西 西安 710072)
0 引言
现有可用的水下通信方式主要包括电磁波通信、声通信、无线光通信及光纤通信等。与其他通信方式相比,光纤通信具有传输距离远、信息传输速率高、体积小、质量轻等优点[1],特别适合有大容量信息传输需求的场合。近年来,利用深海潜水器进行试验和深海科考,往往需要将视频等大容量信息实时回传给母船,母船也会根据需要对潜水器进行遥控操作[2],采用水下动态有线通信技术,在潜水器和母船上分别携带一个光纤线团,在潜水器航行时,两侧线团内光纤微缆受流体作用分别布放,建立潜水器与母船间的动态通信链路(见图1)。光纤线团采用轴向内放线方式,由单根光纤微缆分层双向紧密绕制而成,使用时光纤微缆从线团内腔顺次逐匝逐层布放,其布放性能直接影响信道构建的可靠性,是由线团绕制质量直接决定的。

图1 潜水器光纤有线通信示意图Fig.1 Schematic diagram of fiber-optic cable communication of unmanned submersible vehicle
缆索缠绕力学、成型性能以及影响因素方面的研究成果较多。制导光缆缠绕方面,马成举等建立了卷盘层间压强模型,考虑光缆、卷盘的径向变形因素,采用光栅传感技术对绕线过程光缆层压强进行试验验证[3];胡君良等对缠绕过程光缆和线轴受力情况进行了分析[4],并根据缠绕时光缆的应变情况计算线包传输附加损耗[5]。复合增强材料缠绕方面主要研究内衬和复合材料的各向应力状态,分析内压、热应变等载荷以及内衬厚度、缠绕角度、缠绕张力、纤维体积含量等结构工艺参数对应力、应变、变形分布的影响[6-13],优化设计及工艺,提高承压件性能。光纤陀螺中光纤环的缠绕受缠绕张力影响较大,通过建立光纤环缠绕受力模型,分析缠绕张力对光纤环应力影响,提出合理的缠绕张力控制方法并进行试验验证[14-16]。起重机等重型机械通过卷筒缠绕钢丝绳提升重物,分析钢丝绳缠绕过程的张力变化以及卷筒和端板的受力情况,优化卷筒结构,提高可靠性和安全性[17-19]。与上述研究相比,潜水器用光纤线团在结构和绕制方式上有明显差异。潜水器用光纤线团(见图2)采用单根光纤微缆精密紧密缠绕,光纤微缆层间、匝间均接触,且存在两侧端板的结构限制。线团绕制时需对绕入的光纤微缆施加一定的预紧力,在这个力作用下光纤线团层与层、匝与匝之间的光纤微缆会相互挤压,使内层光纤微缆产生放松效应,并对两侧端板产生挤压,在每层光纤微缆径向、轴向挤压双重作用下,光纤线团内部应力分布状态较为复杂,呈非线性。上述缠绕力学研究成果无法直接应用于潜水器用光纤线团力学分析及研究。

图2 光纤线团及绕制结构Fig.2 Fiber-optic coil and winding mechanism
光纤线团的应力分布状态是影响光纤线团绕制质量的重要因素,决定其使用及贮存寿命[20]。在绕制机构结构确定的前提下,通过改变绕制预紧力和光纤微缆自身弹性参数能够有效调整光纤线团的应力分布,改变应力线型和幅值,使其趋于合理。因此,研究绕制张力和光纤微缆弹性参数对光纤线团应力分布的影响,对于光纤微缆结构和光纤线团绕制工艺的优化设计及改进具有重要参考价值。
本文基于潜水器用光纤线团两侧端板限制的结构形式,在计算光纤线团应力时除了分析光纤微缆沿线团的径向变形,同时还考虑光纤微缆沿线团的轴向变形,分别对光纤微缆径向承压和受端板限制的轴向挤压进行受力分析,以光纤微缆沿线团径向变形与其应力的关系以及沿线团轴向变形与端板变形关系联立形成光纤线团应力解算方程,在此基础上对光纤微缆轴向、截面变形涉及的轴向弹性模量、径向弹性模量和径向弹性系数等弹性参数进行定义和建模分析。以潜水器用某型光纤线团为对象,分别对光纤线团应力分布随光纤微缆弹性参数和绕制张力的变化规律进行仿真研究,对光纤线团应力分布以及各参数对线团寿命、结构稳定性的影响机理做出了解释。
1 光纤线团内部应力分布
光纤微缆在绕制工装内分层密绕,下层光纤微缆承受上层光纤微缆的压力,其截面发生沿线团的径向压缩变形,使下层光纤微缆周向应变减小,应力减小,对其内层光纤微缆的压力也减小,而两侧端板的存在,限制光纤微缆沿线团轴向的截面变形,减小光纤微缆的径向压缩变形,因此各层光纤微缆的应力与所承受压力并不是线性相关的。
当前绕入光纤线团的光纤微缆受力如图3所示,对下层光纤微缆施加的压力dFp为
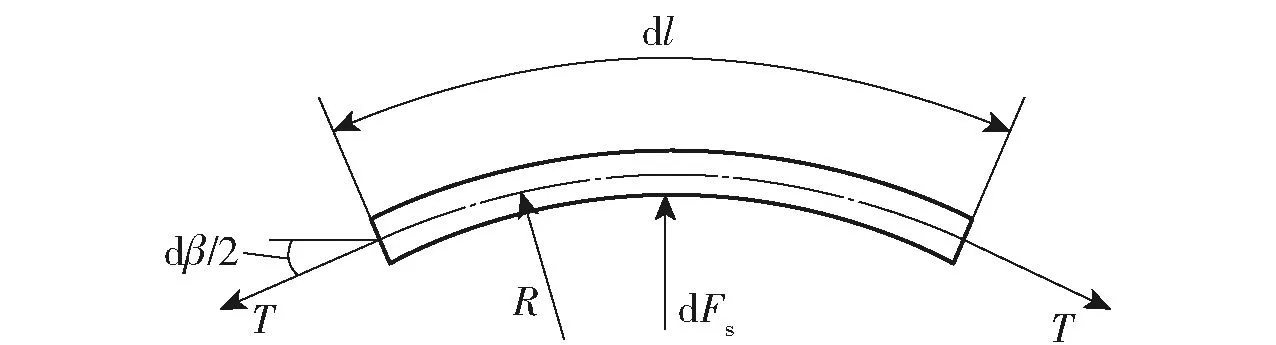
图3 光纤微缆受力Fig.3 Force analysis of fiber-optic micro-cable
(1)
式中:dl为光纤微缆微元的长度;dβ为微元对应的张角;T为绕制张力;R为绕制半径;dFs为微元所受的支持力。
光纤线团光纤微缆间作用力如图4所示。图4中:Fc为层间光纤微缆接触点挤压力;Ff为层间光纤微缆接触点摩擦力;Fe为同层光纤微缆匝间沿线团轴向的挤压力;Fo,r为光纤微缆受外层作用力沿线团径向的分量;Fo,z为光纤微缆受外层作用力沿线团轴向的分量;α为光纤微缆的堆叠角。
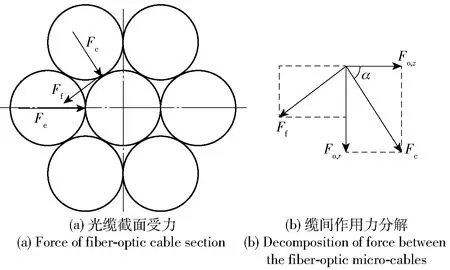
图4 光纤微缆间作用力Fig.4 Force between the fiber-optic micro-cables
光纤线团光纤微缆间作用力沿线团径向、轴向进行分解,即
(2)
式中:μs为光纤微缆间静摩擦系数。
光纤线团绕制时,各层光纤微缆均会对内层施加压力。当光纤线团绕制n层时,第i层光纤微缆所受压力是其外层各层光纤微缆张力沿线团径向的合力。第n层光纤微缆绕制时对n-1层施加的压力为Tdβ,则第i层光纤微缆所承受的压力变化量为
(3)
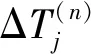

图5 光纤微缆截面受力状态Fig.5 Force analysis of fiber-optic micro-cable section
依据图5和(2)式可得
(4)

(5)

同样地,可得到光纤微缆沿线团轴向变形,即
(6)
光纤线团的两侧端板限制各层光纤微缆沿线团的轴向变形,使光纤微缆与端板之间存在轴向作用力。芯轴、绕制工装与端板之间固连,绕制工装的弹性模量远大于端板,分析时忽略绕制工装的变形,而当前层光纤微缆绕入时对端板无轴向力作用。
在绕制工装外径Rt范围内(即Rm≤Ri≤Rt,Rm为芯轴外径,Ri为第i层光纤微缆的半径),端板受光纤微缆的轴向力作用而产生挤压变形为
(7)
式中:Er为端板的弹性模量;Hr为端板厚度;nt为Rt对应的光缆层数;
(8)

(9)
绕制工装范围以外端板受各层光纤微缆的轴向力而产生弯曲变形,依据圆形板对称弯曲理论,光纤线团绕制第n层时第i层光纤微缆轴向力作用下端板在半径r处的挠度为
(10)


(11)

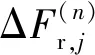
(12)
式中:Rj为第j层光纤微缆的半径。
则绕制第n层时第i层光纤微缆对应端板处的弯曲变形为
(13)
不考虑芯轴的径向变形,第i层光纤微缆在绕制第n层时应力减小量与该层径向变形相关,即
(14)

(15)
而该层光纤微缆的张力减小量为
(16)
式中:So为光缆截面面积。
光纤微缆沿线包的轴向变形等于两侧端板对应位置的变形之和,即
(17)

(14)式和(17)式联立,即可求解绕制第n层时各层光纤微缆的应力减小量。每层光纤微缆在后续层绕制时其应力均会减小,在绕制第n层光纤微缆后,第i层光纤微缆的应力为
(18)
式中:σT为绕制张力T作用下光纤微缆的拉伸应力,σT=T/So.
2 光纤微缆弹性参数及绕制时光纤微缆的变形
光纤微缆弹性参数用于描述光缆轴向、径向的弹性特性。如(14)式所示,绕制时光纤微缆的应力变化与其轴向弹性模量Eo,z相关。光纤微缆由光纤和护套组成,光纤包括纤芯和包层,护套紧包在光纤上。Eo,z可经拉伸试验获取,也可通过(19)式近似计算。
(19)
式中:Ef、Ec、Es分别为纤芯、包层、护套的弹性模量;Sf、Sc、Ss分别为纤芯、包层、护套的截面积;So=Sf+Sc+Ss.
要计算光纤线团绕制时光纤微缆沿线团径向、轴向的变形量,需分析光纤微缆径向受力与变形的关系以及光纤微缆沿线包径向和轴向变形之间的关系,引入光纤微缆的径向弹性参数:径向弹性模量和径向弹性系数。径向弹性特性如图6所示。
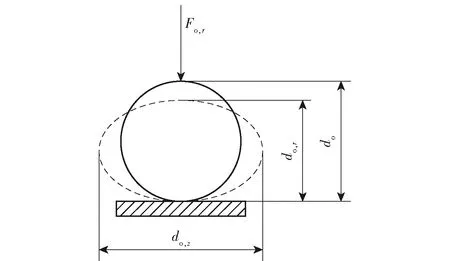
图6 径向弹性特性Fig.6 Radial elastic property
如图6所示,定义光纤微缆单位长度上的压力与沿压力方向的截面直径减小量的比值为径向弹性模量Eo,r,即
(20)
式中:l为受压光纤微缆长度。在压力Fo,r作用下,光纤微缆沿压力方向截面直径由do变化为do,r.
压力垂直方向的光纤微缆截面直径增加量与压力方向的截面直径减小量的比值定义为径向弹性系数Wo,r,即
(21)
光纤微缆沿与压力垂直方向截面直径由do变化为do,z.
光纤微缆的径向弹性模量和弹性系数可通过有限元仿真计算获得,将光纤微缆夹持在两个压块之间,上压块施加压力,下压块下表面固定,光纤微缆各层间采用粘合约束(见图7),测量施加压力后光纤微缆沿压力方向和垂直压力方向的直径变化,从而得出光纤微缆的径向弹性参数。

图7 径向弹性特性分析模型Fig.7 Analysis model of radial elastic property

(22)
式中:dli为张角dβ对应的第i层光纤微缆微元的长度,dli=Ridβ.

(23)
综上所述,桥梁大体积混凝土承台施工的温控措施对工程质量起着非常重要的作用。为有效防止温度裂缝产生,保证大体积承台混凝土施工质量,做好温度控制,降低水化热是桥梁承台施工的关键。通过分析本工程的施工控制可知,通过严格控制混凝土浇筑温度、降低水泥水化热、混凝土养生、埋设冷却管降温、采用科学的监测方法、合理布置监测点、注意监测频率以及加强监控与反馈等措施,可以有效控制温度裂缝,保证桥梁大体积混凝土承台施工顺利完成,确保工程施工质量。
(24)
(25)

(26)
(27)
(28)
3 光纤线团应力分布影响分析
(14)式和(17)式联立,可得到形如(29)式的多元线性方程组,用于求解第n层绕制时各层光纤微缆的应力和轴向挤压力增量。
(29)

光纤线团某层光纤微缆的应力与后续层绕制导致该层光纤微缆的应力减小量相关(见(18)式),各参数对光纤线团应力分布的影响无法直接从模型中获得。
当绕制机构结构参数确定时,光纤线团应力分布由光纤微缆弹性特性和绕制张力决定,当Eo,z、Eo,r、Wo,r、T中任一参数改变时,光纤线团的应力线型和幅值随之改变。为揭示光纤线团应力分布随各影响因素的变化规律,分别对各参数变化时线团应力进行仿真分析。仿真参数见表1,绕制层数为100层。

表1 仿真参数Tab.1 Simulation parameters
3.1 光纤微缆弹性特性的影响
3.1.1 轴向弹性模量
设定绕制张力T=10 N,径向弹性模量Eo,r=0.5 GPa,径向弹性系数Wo,r=0.5,光纤线团应力σ分布随光纤微缆轴向弹性模量Eo,z的变化情况如图8所示。

图8 光纤线团应力分布与轴向弹性模量的关系Fig.8 Relationship between stress distribution of fiber-optic coil and axial elastic modulus of fiber-optic micro-cable
不同轴向弹性模量Eo,z下光纤线团应力σ分布对比如图9所示。对于不同光纤微缆轴向弹性模量,光纤线团应力分布线型和变化趋势是相似的,均为类似“抛物线”线型,应力随层数i先减小,而斜率Δσ从负值逐渐增大,当斜率Δσ为0时应力σ达到最小值,然后应力σ和斜率Δσ逐渐增大,直至最外层应力σ达到最大,这是由径向变形量和变形次数决定的。由图9可知,光纤微缆轴向弹性模量越大,应力曲线越陡,除最外层外同层光纤微缆应力越小,最小应力向内层移动,相邻层应力变化量越大。这是由于轴向弹性模量增大,(29)式中A(n)的对角线系数减小,使绕制过程各层光纤微缆应力减小量增大,导致各层光纤微缆的应力减小。由ε=σ/Eo,z得出不同轴向弹性模量Eo,z下光纤线团应变ε对比曲线(见图10),光纤微缆轴向弹性模量越大,各层应变均减小,应变曲线下移且趋于平缓,相邻层应变变化量越小。这是由于轴向弹性模量增大使各层光纤微缆应力减小量增大、径向压缩量减小,从而使光纤线团各层光纤微缆的应力减小,应变曲线更平缓。

图9 不同轴向弹性模量下光纤线团应力分布对比Fig.9 Comparison of stress distributions of fiber-optic coil with different axial elastic modulii of fiber-optic micro-cable

图10 不同轴向弹性模量下光纤线团应变分布对比Fig.10 Comparison of strain distributions of fiber-optic coil with different axial elastic modulii of fiber-optic micro-cable

图11 光纤线团浴盆特征参数随轴向弹性模量的变化Fig.11 Variation of bathtub feature parameter of fiber-optic coil with axial elastic modulus of fiber-optic micro-cable
3.1.2 径向弹性模量
设定绕制张力T=10 N,轴向弹性模量Eo,z=10 GPa,径向弹性系数Wo,r=0.5.
图12反映了光纤线团应力分布随光纤微缆径向弹性模量的变化情况,具体对比见图13. 由图13可知,不同径向弹性模量的光缆线包应力分布线型和变化趋势是相似的,均为类似“抛物线”线型,光纤微缆径向弹性模量越大,应力曲线越平缓,除最外层外同层光纤微缆应力越大,最小应力向外层移动,相邻层应力变化量越小。这是由于增大径向弹性模量会使各层光纤微缆径向变形量减小,从而使各层光纤微缆应力减小量减小,导致各层光纤微缆应力增大。光纤线团浴盆特征参数随径向弹性模量的变化如图14所示。由图14可知,随着光纤微缆径向弹性模量的增大,浴盆特征参数先明显减小,然后缓慢减小并趋近于1.

图12 光纤线团应力分布与径向弹性模量的关系Fig.12 Relationship between stress distribution of fiber-optic coil and radial elastic modulus of fiber-optic micro-cable
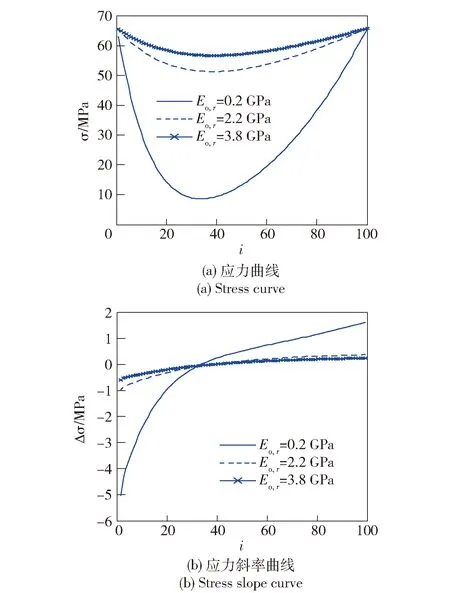
图13 不同径向弹性模量下光纤线团应力分布对比Fig.13 Comparison of stress distributions of fiber-optic coil with different radial elastic moduii of fiber-optic micro-cable

图14 光纤线团浴盆特征参数随径向弹性模量的变化Fig.14 Variation of bathtub feature parameter of fiber-optic coil with radial elastic modulus of fiber-optic micro-cable
3.1.3 径向弹性系数
设定绕制张力T=10 N,轴向弹性模量Eo,z=10 GPa,径向弹性模量Eo,r=0.5 GPa,光纤线团应力分布随光纤微缆径向弹性系数的变化情况如图15所示。

图15 光纤线团应力分布与径向弹性系数的关系Fig.15 Relationship between stress distribution of fiber-optic coil and radial elastic coefficient of fiber-optic micro-cable
光纤线团应力分布随径向弹性系数的变化趋势(见图16)与径向弹性模量相似,径向弹性系数越大,应力曲线越平缓,除最外层外同层光纤微缆应力越大,最小应力向外层移动,相邻层应力变化量越小。这是由于径向弹性系数的增大会使轴向力引起的光纤微缆径向延伸量增大,造成各层光纤微缆径向变形的减小,从而使应力减小量减小,导致各层光纤微缆应力增大。光纤线团浴盆特征参数随径向弹性系数的变化如图17所示。由图17可知,随着径向弹性系数的增大,浴盆特征参数逐渐减小,光纤微缆径向弹性系数越大,光纤线团浴盆特征参数越接近1.

图16 不同径向弹性系数下光纤线团应力分布对比Fig.16 Comparison of stress distributions of fiber-optic coils with different radial elastic coefficients of fiber-optic micro-cable

图17 光纤线团浴盆特征参数随径向弹性系数的变化Fig.17 Variation of bathtub feature parameter of fiber-optic coil with radial elastic coefficient of fiber-optic micro-cable
从光纤角度来看,在绕制张力相同条件下,光纤微缆轴向弹性模量越大,径向弹性模量和径向弹性系数越小,光纤线团整体应力越小,贮存寿命越长。光纤线团作为一个整体,其贮存寿命还需考虑光纤线团的结构稳定性,应力分布的浴盆特征是一个重要判据,光纤微缆轴向弹性模量越小,径向弹性模量和径向弹性系数越大,浴盆特征越明显,线团结构越稳定,更有利于光纤线团的贮存。而光纤微缆的弹性参数间也是相关联的,均与光纤微缆结构及各层材料特性有关。在光纤微缆设计时,首先保证光纤线团结构稳定性,并尽量减小光纤线团内部应力水平,以提高光纤线团的贮存寿命。
3.2 绕制张力的影响
设定轴向弹性模量Eo,z=10 GPa,径向弹性模量Eo,r=0.5 GPa,径向弹性系数Wo,r=0.5,光纤线团应力分布随绕制张力的变化情况如图18所示。

图18 光纤线团应力分布与绕制张力的关系Fig.18 Relationship between stress distribution of fiber-optic coil and winding tension
不同绕制张力下光纤线团应力分布对比如图19所示。由图19可知:不同绕制张力的光纤线团应力均呈类似“抛物线”线型,绕制张力越大,应力曲线越陡;同层光纤微缆应力越大,相邻层应力变化量越大,不同绕制张力的应力分布曲线最小应力对应层数相同。由(29)式可知,绕制张力增大,各层光纤微缆的应力减小量增大,因此应力曲线越陡。

图19 不同绕制张力下光纤线团应力分布对比Fig.19 Comparison of stress distributions of fiber-optic coil with different winding tensions
(29)式可改写为
(30)

则
(31)
由(31)式可知,归一化后,光纤线团的应力分布仅与Ω(n)和Θ(n)相关,即与绕制机构结构参数和光纤微缆弹性参数相关,而与绕制张力的大小无关。不同绕制张力下的浴盆特征参数是相同的,然而绕制张力的增大会使光纤线团内部应力整体增大,降低光纤线团的寿命。
绕制张力越大,光纤线团各层应力越大,贮存寿命越短。因此需选择较小的绕制张力,以提高光纤线团的贮存寿命。然而光纤微缆具有一定的弯曲刚度,绕制张力较小时,无法将光纤微缆紧密缠绕在线团上,反而降低了光纤线团的绕制质量。在绕制参数设计时,应在满足光纤微缆紧密缠绕的前提下尽量减小绕制张力。
4 线团绕制实测数据分析
用两根弹性参数不同的光纤微缆以相同张力绕制两个结构尺寸相同的线团,测量绕制后线团的应力分布,对每层长度范围内的应力进行平均,获得光纤线团层均应力分布曲线,并与仿真曲线进行对比,如图20所示。两个线团所用光纤微缆弹性参数见表2,图20中仿真曲线的仿真参数与表1相同。
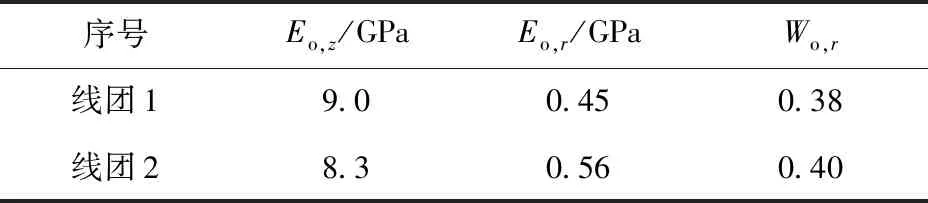
表2 实验用光纤微缆弹性参数Tab.2 Elastic parameters of experimental fiber-optic micro-cables

图20 采用不同弹性参数光纤微缆的线团应力分布实测与仿真结果对比Fig.20 Comparison of measured and simulated results of stress distributions of fiber-optic coils with different elastic parameters of fiber-optic micro-cables
由图20可知,光纤线团实测应力数据随层数的变化趋势和整体线型与仿真结果是一致的,数值上偏差较小。实测结果存在偏差主要与绕线设备的张力控制精度以及光纤微缆轴向长度上弹性参数波动相关。对应光纤微缆不同的弹性参数,线团绕制后整体应力分布的变化符合前述仿真分析的结论。
两个线团实测、仿真的浴盆特征参数如表3所示。由表2和表3可知,在绕制张力相同的条件下,线团2所用光纤微缆的轴向弹性模量较小,径向弹性模量和径向弹性系数较大,对比线团1,应力实测结果的浴盆特征参数更接近1,与前述仿真分析结论是一致的。

表3 线团实测与仿真浴盆特征参数Tab.3 Bathtub feature parameters of measured and simulated results of fiber-optic coils
5 结论
光纤线团应力分布状态是体现光纤线团绕制质量的重要因素。本文通过对光纤微缆和端板的受力分析,建立光纤线团应力分析模型,分析光纤微缆弹性参数和绕制张力对光纤线团应力分布的影响,并开展线团绕制试验实测应力加以对比。得出以下主要结论:
1)从不同光纤微缆弹性参数和绕制张力仿真数据看,光纤线团应力分布呈类抛物线线型,最外层应力最大,应力曲线最低点更靠内层。
2)从仿真结果看,光纤微缆轴向弹性模量越小、径向弹性模量和弹性系数越大,有利于光纤线团的结构稳定,但会降低光纤的贮存寿命,而绕制张力越大会降低光纤的寿命,但并不影响光纤线团的结构稳定性。
3)对不同弹性特性光纤微缆绕制的线团进行了实验室测量,线团应力分布和浴盆特征参数随光纤微缆弹性特性的变化与仿真分析结论一致,验证了应力模型和仿真分析的准确性。
4)在仿真分析的基础上,提出了光纤微缆和绕制张力设计的优化方向。在光纤微缆设计时,首先保证光纤线团结构稳定性,即减小光纤微缆轴向弹性模量,并增大径向弹性模量和径向弹性系数,在此基础上尽量平衡各弹性参数间关系,降低光纤线团整体应力水平;然后在绕制参数设计时,应在确保光纤微缆能够紧密缠绕的前提下尽量减小绕制张力。
本文研究能够为潜水器用光纤线团设计及应力分析、光纤微缆结构设计、绕制工艺设计等方面提供理论参考,为后续光纤线团的等应力绕制研究奠定基础,同时本文涉及的研究方法也可为其他领域缠绕力学特性分析提供借鉴和参考。
参考文献(References)
[1] 高卓,汤伟江,朱云周,等.微细光缆在水下航行器中的应用及关键技术综述[J].水下无人系统学报,2017,25(5):385-395.
GAO Z,TANG W J,ZHU Y Z,et al.Overview of applications of fiber optic micro-cable in undersea vehicle and key technologies[J].Journal of Unmanned Undersea Systems,2017,25(5):385-395.(in Chinese)
[2] 李一平,李硕,张艾群.自主/遥控水下机器人研究现状[J].工程研究——跨学科视野中的工程,2016,8(2):217-222.
LI Y P,LI S,ZHANG A Q.Research status of autonomous &remotely operated vehicle[J].Journal of Engineering Studies,2016,8(2):217-222.(in Chinese)
[3] MA C J,REN L Y,QU E S,et al.Modeling and testing of static pressure within an optical fiber cable spool using distributed fiber Bragg gratings[J].Optics Communications,2012,285(24):4949-4953.
[4] 胡君良,马恒坚,崔得东.制导光缆线包中光缆受力分析与线轴设计[J].光通信研究,1997(3):35-39.
HU J L,MA H J,CUI D D.Force analysis on optical fiber cable in the control and guide cable pack and design of spool[J].Study on Optical Communications,1997(3):35-39.(in Chinese)
[5] 胡君良,马恒坚,崔得东.制导光缆线包光附加损耗分析与计算[J].应用光学,1998,19(6):44-47.
HU J L,MA H J,CUI D D.Analysis and calculation of excess loss about the control and guide cable pack[J].Journal of Applied Optics,1998,19(6):44-47.(in Chinese)
[6] BAKAIYAN H,HOSSEINI H,AMERI E.Analysis of multi-la-yered filament-wound composite pipes under combined internal pressure and thermomechanical loading with thermal variations[J].Composite Structures,2009,88(4):532-541.
[7] ANSARI R,ALISAFAEI F,GHAEDI P.Dynamic analysis of multi-layered filament-wound composite pipes subjected to cyclic internal pressure and cyclic temperature[J].Composite Structures,2010,92(5):1100-1109.
[8] LIU C,SHI Y Y.Design optimization for filament wound cylindrical composite internal pressure vessels considering process-induced residual stresses[J].Composite Structures,2020,235:111755.
[9] BOUHAFS M,SEREIR Z,CHATEAUNEUF A.Probabilistic analysis of the mechanical response of thick composite pipes under internal pressure[J].International Journal of Pressure Vessels and Piping,2012,95:7-15.
[10] 吴杨,邢静忠,耿沛,等.考虑纤维体积含量变化的纤维缠绕厚壁柱形结构的等强度设计[J].复合材料学报,2015,32(3):789-796.
WU Y,XING J Z,GENG P,et al.Constant strength design of filament wound thick-walled cylindrical structure considering variation of fiber volume content[J].Acta Materiae Compositae Sinica,2015,32(3):789-796.(in Chinese)
[11] ZU L,XU H,ZHANG B,et al.Design of filament-wound composite structures with arch-shaped cross sections considering fiber tension simulation[J].Composite Structures,2018,194:119-125.
[12] GHASEMI A R,ASGHARI B,TABATABAEIAN A.Determination of the influence of thermo-mechanical factors on the residual stresses of cylindrical composite tubes:experimental and computational analyses[J].International Journal of Pressure Vessels and Piping,2020,183:104098.
[13] 李博,熊超,殷军辉,等.多角度交替缠绕复合圆筒的剩余应力算法及水压试验[J].复合材料学报,2018,35(6):1452-1463.
LI B,XIONG C,YIN J H,et al.Residual stress algorithm for composite cylinder with alternate multi-angle winding layers and water-pressure test[J].Acta Materiae Compositae Sinica,2018,35(6):1452-1463.(in Chinese)
[14] JIA M,YANG G L.Research of optical fiber coil winding model based on large-deformation theory of elasticity and its application[J].Chinese Journal of Aeronautics,2011,24(5):640-647.
[15] 孟照魁,张春熹,杨远洪,等.光纤环绕制过程中的张力分析[J].北京航空航天大学学报,2005,31(3):307-310.
MENG Z K,ZHANG C X,YANG Y H,et al.Analysis of stress in winding fiber-optic ring[J].Journal of Beijing University of Aeronautics and Astronautics,2005,31(3):307-310.(in Chinese)
[16] 温泽强,杨瑞峰,贾建芳.基于键合图的光纤环绕制小张力控制结构的建模和仿真[J].测控技术,2012,31(3):119-127.
WEN Z Q,YANG R F,JIA J F.Building and simulating the model of the tension control during winding a fiber optic sensor coil based on the bond graph[J].Measurement &Control Technology,2012,31(3):119-127.(in Chinese)
[17] 严兵,姚海.浮式起重机篱笆式卷筒的结构强度及稳定性分析[J].船舶工程,2012,34(增刊2):204-208.
YAN B,YAO H.Study on strength and stability of LeBus grooved drum applied in offshore crane[J].Ship Engineering,2012,34(S2):204-208.(in Chinese)
[18] 朱洪军,鲁聪达,刘健.篱笆式卷筒结构的动态特性研究[J].船舶工程,2013,35(2):51-58.
ZHU H J,LU C D,LIU J.Study on dynamic characteristics of LeBus grooved drum structure[J].Ship Engineering,2013,35(2):51-58.(in Chinese)
[19] 龚宪生,罗宇驰,吴水源.提升机卷筒结构对多层缠绕双钢丝绳变形失谐的影响[J].煤炭学报,2016,41(8):2121-2129.
GONG X S,LUO Y C,WU S Y.Effect of drum structure of mine hoist on multilayer winding and multipoint lifting ropes’ discordance[J].Journal of China Coal Society,2016,41(8):2121-2129.(in Chinese)
[20] MATTHIJSSE P,GRIFFIOEN W.Matching optical fiber lifetime and bend-loss limits for optimized local loop fiber storage[J].Optical Fiber Technology,2005,11(1):92-99.

