惯性颗粒和壁湍流的相互作用:湍流调制及颗粒分布
王贵全
(荷兰特文特大学 流体物理课题组,恩斯赫德 7500AE,荷兰)
0 引 言
惯性粒子在壁面湍流中的流动可用于研究沙粒在河流中的沉积、雨雪的沉积速度与分布、沙尘在地球以及火星近地面层中的传输以及空气污染物在城市上空的分布等很多与地球物理、工程领域以及环境科学相关的重要问题[1-4]。实验研究主要侧重于流体/粒子的平均速度和雷诺应力,以及粒子的分布,然而由于颗粒聚集与群聚效应以及壁面的影响,导致实验研究的难度增加,限制了实验研究的发展[5]。随着计算能力的不断提高,直接数值模拟壁面湍流耦合惯性点粒子可以达到中等湍流雷诺数Reτ~O(103)(根据壁面黏性尺度),耦合颗粒数目可以达到O(108)以上,可以看到直接数值模拟已经成为一个有效的技术手段被应用于探究湍流粒子两相流动这个非常复杂的物理问题,其不仅可以捕捉到最小的流动尺度,分析颗粒在湍流中的分布状态,也可以用于研究粒子对湍流的调制。
对于惯性粒子,本文假设颗粒密度远大于流体相密度,颗粒尺度远小于湍流最小耗散尺度,在上述假设条件下,惯性粒子可被近似为点粒子,这样可以极大地简化颗粒相的数值模型。而随着颗粒相浓度的下降,粒子与粒子间的相互作用力以及粒子对流体间的反作用力也可以逐渐的被忽略,这样同样也会提高计算效率。Elghobashi[6]根据颗粒相浓度的不同,将粒子与流动的耦合分为:四向耦合(同时考虑粒子对流体的反馈力以及粒子之间的相互作用力)、双向耦合(不考虑粒子之间的相互作用力)以及单向耦合(不考虑粒子对流体的反馈力以及粒子之间的相互作用力)。本文应用直接数值模拟和拉格朗日点粒子跟踪方法对惯性粒子在壁面湍流这一复杂问题进行研究,主要关注粒子对湍流的调节机制及粒子分布。对湍流的调制主要研究粒子惯性对湍流内层大尺度结构LSMs以及外层超大尺度结构VLSMs的影响。对粒子分布的研究包含两部分:一是粒子聚集,这里指粒子在壁面垂直方向由于湍流场导致的浓度不均匀;二是粒子群聚形态,这里指粒子在水平截面上由于湍流场导致的不均匀分布形态。本文是对作者以往开展的相关研究工作进行小结[7-13],结构安排如下:第1节介绍此工作采用的数值方法及验证过程(单向、双向及四向耦合),第2节讨论粒子对湍流内层LSMs与外层VLSMs的调制机理(双向耦合),第3节分析粒子在LSMs与VLSMs中的分布(双向耦合),第4节关注粒子在重力驱动下的沉积速度(单向耦合)。
1 数值模拟方法及验证
1.1 数值方法
1.1.1 流体相
采用直接数值模拟对不可压缩流体求解,流向(x)和展向(z)采用周期性边界条件并应用谱方法求解,壁面垂直方向(y)采用二阶有限差分格式,时间推进采用三阶Runge-Kutta格式。不可压缩条件通过求解压力泊松方程来满足。求解的连续方程和动量方程分别为:
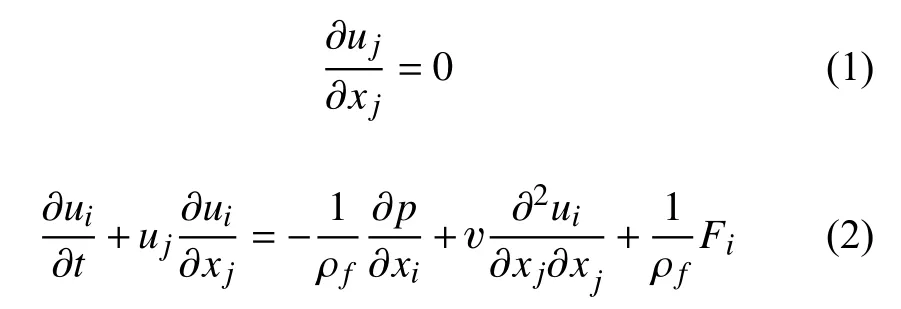
其中ui为流体速度,p为压力,Fi为粒子对流体相的反作用力,v是 流体动力学黏度, ρf是流体的密度。
1.1.2 颗粒相
当粒子的密度远大于流体相密度、粒子的尺度远小于最小的湍流耗散尺度,粒子被近似为点粒子。此时只考虑Schiller-Naumann曳力模型,粒子的速度和轨迹可以通过积分如下方程:
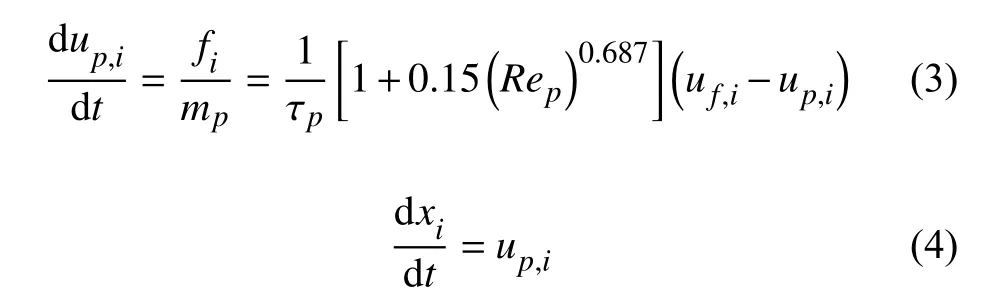
在研究壁面湍流耦合惯性粒子这一问题时,最重要的控制参数为粒子的斯托克斯数(Stokes number,St),定义为粒子的特征时间尺度( τp)和流场特征时间尺度( τf)的比值。而由于壁面湍流边界层内部区域与外部区域存在不同的流场特征时间尺度,为了研究粒子与不同湍流尺度的耦合作用,定义了如下三个粒子斯托克斯数:

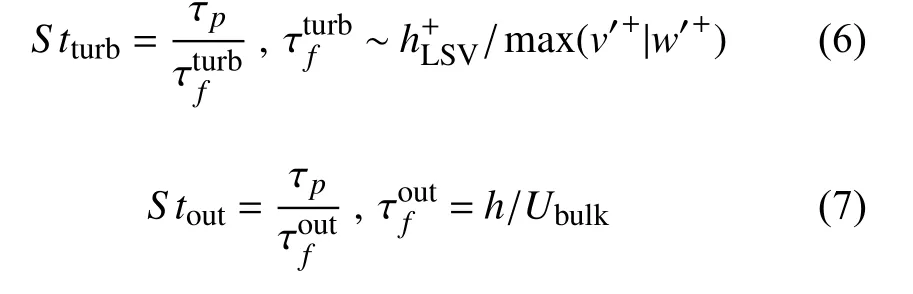
1.2 模型验证[7]
在二维耦合模型中,点粒子方法是将点力耦合到最近的欧拉网格点上,忽略粒子体积对流体的扰动,除了上述传统的点粒子方法,Capecelatro[14]介绍了一种体积平均方法,在计算粒子力的时候,不仅考虑曳力模型,同时考虑粒子大小对本地压力和黏性应力的影响,通过高斯核函数耦合到欧拉网格点上。Gualtieri[15]介绍了一种正则化点粒子方法,在计算中通过多极展开获得球的斯托克斯流动的一阶偶极子来近似点粒子对远场的扰动。上述两种或其他的改进点粒子方法一般都是尝试通过引入模型来考虑粒子的体积效应,但弊端是大大增加了计算量。为了验证传统的点粒子方法在模拟壁面湍流耦合粒子问题时的准确性,我们对传统点粒子方法与体积平均方法[14]以及实验结果[16]进行了比较,验证过程及参数如下:
(1) 首先与已发表的采用传统点粒子方法的结果[17]进行比较,目的是验证代码编写的正确性。参数为Reτ= 180、St+= 30、双向耦合。与文献[17]比较了流体相与粒子相的平均速度及脉动速度,得到了几乎一致的结果;
(2) 进一步比较传统点粒子方法与体积平均方法[14],来了解忽略颗粒体积效应对模拟结果的影响。参数为Reτ= 630、St+= 2030以及Reτ= 227、St+= 58.6,四向耦合。与文献[14]比较了流体相与粒子相的平均速度及脉动速度,得到了几乎一致的结果;
(3) 将传统点粒子方法、体积平均方法[14]与实验结果[16]进行一对一的比较。参数为Reτ= 227、St+=58.6,模拟中采用四向耦合。比较了粒子浓度曲线,粒子聚集与群聚等稳态值(箱形计数法,冯洛诺伊图,概率密度函数,径向分布函数),发现两种模拟得到的结果近乎一致。但与实验结果相比,尤其是在近壁面处,粒子的壁面垂直脉动速度以及粒子的浓度有差别,可能的原因有—数值模拟中没有正确考虑湍流湍泳以及近壁面升力的影响[18],或者实验中静电效应以及近壁面由于粒子聚集导致测量不够精确。对点粒子模型在近壁面处的修正是个一直没有解决的问题,一种可能适用的方法是将小粒子看作有限大小粒子进行捕捉界面研究,但是小粒子的尺度远小于湍流最小耗散尺度,这样做会导致难以承受的计算网格数量,据作者所知,目前还缺乏相关的研究工作。
综上,在粒子壁面湍流中,在St+= O(10~103)区间内,传统的点粒子方法和改进的点粒子方法获得的粒子的速度与浓度一阶、二阶稳态量以及流体相的速度一阶、二阶和三阶稳态量几乎一致。由于传统点粒子方法可以节省大量的计算时间,使得在直接数值模拟中可以引入更多数量的粒子,因此在本文的研究中,将采用这种数值方法。
1.3 计算域尺度选择[8]
湍流内层的大尺度结构(LSMs)和湍流外层的超大尺度结构(VLSMs)的存在导致流体的一阶与二阶稳态值依赖于计算域的尺寸[19]。图1展示了瞬时流向脉动速度的云图在湍流内层与外层、四种计算域尺寸下的模拟结果:超大尺寸Lx= 12πh,Lz= 3πh;大尺寸Lx= 6πh,Lz= 3πh;中尺寸Lx= 6h,Lz= 3h;小尺寸Lx= 2.5h,Lz= 1.5h。在湍流内层(y+= 55处水平截面),可以看到,小计算域图1(d)只能捕捉一对高低速条带(高低速条带是由于流向涡结构将近壁面低速流体“上扬”到远壁面的位置,或将远壁面高速流体“下扫”到近壁面的位置),中等以上的计算域图1(a-c)可以得到大于三对以上的高低速条带。在湍流外层(y+= 275处水平截面):小计算域得不到正确的高低速条带;中等计算域在展向方向可以捕捉到一对高低速条带,但是流向方向有截断;大尺度计算域的高低速条带几乎与超大计算域的结果相同,在流向方向几乎没有截断。
在加入粒子后,粒子一阶(平均速度/平均浓度)、二阶稳态(脉动速度)也依赖于计算域的尺寸[20],在已发表的研究成果中,所采用的计算域尺寸也不尽相同(文献[8]的表1列出了文献中常用的计算域尺寸),可以看到,研究计算域尺寸对粒子一阶与二阶稳态值的影响是非常重要的。我们对Reτ= 550、Reτ= 950以及St+= 2.41~908进行了模拟比较[8]。结果显示在单相流中,中等尺寸计算域、大尺寸计算域和超大尺寸计算域的流体的一阶、二阶稳态值几乎相同,而小尺寸计算域会低估流体的一阶、二阶稳态值。当加入粒子以后,流体相二阶稳态量在小尺寸计算域与大尺寸计算域相差较大,颗粒相的近壁面浓度在中尺寸计算域会被低估(10%~20%),尤其是对中高惯性的粒子(St+= 24.2~182),但颗粒相的二阶稳态在中尺寸计算域和大尺寸计算域得到的结果几乎一致。因此,想要精确得到粒子在湍流内层的浓度,需要采用大尺寸计算域。而对于模拟粒子在湍流外层的浓度,中等尺度计算域能得到和大尺度计算域相似的结果。
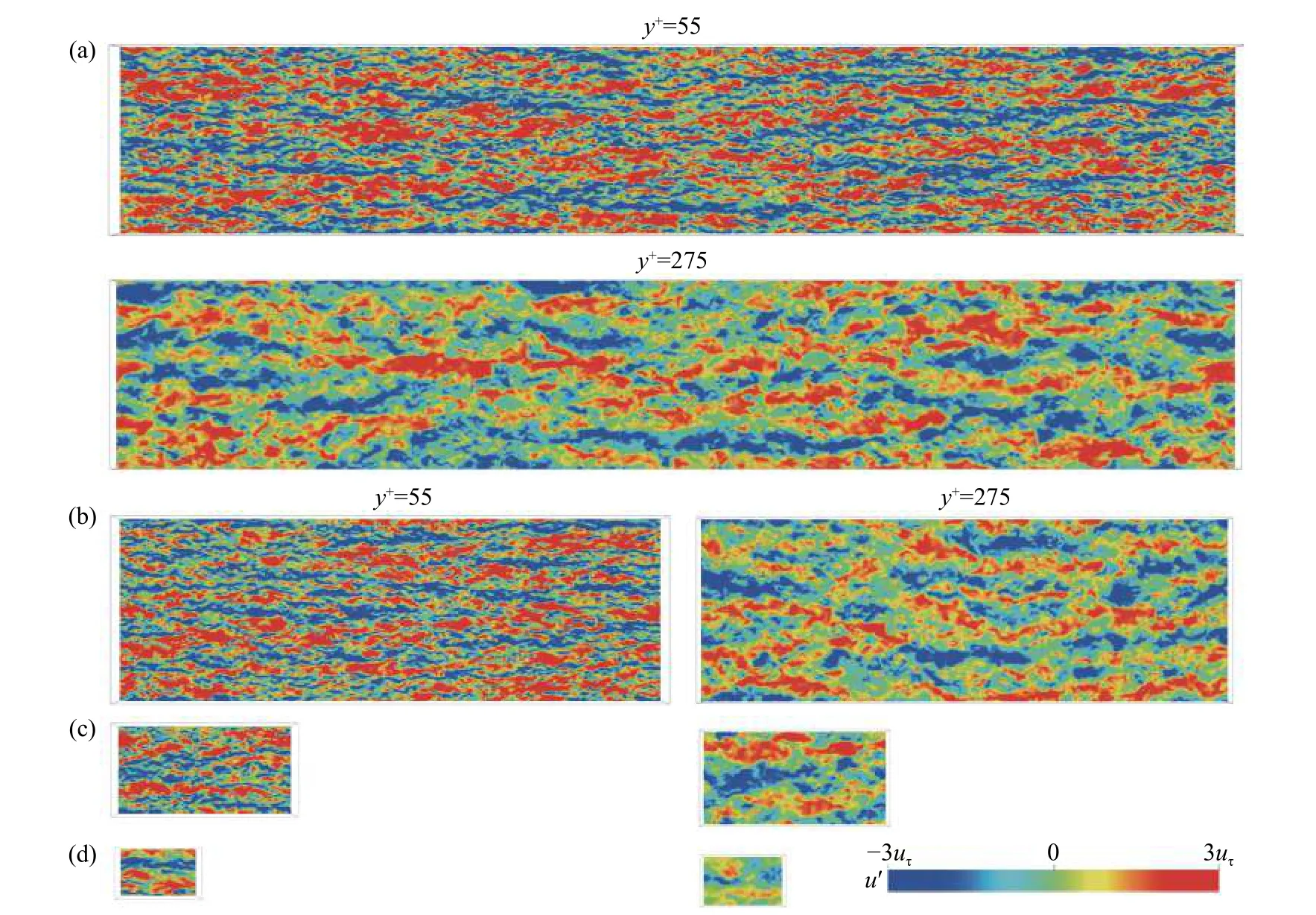
图1 两个壁面垂直位置的横截面的瞬时流向脉动速度云图,y+ = 55和y+ = 275分别代表湍流内层与外层,(a-d)对应于超大尺寸,大尺寸,中尺寸以及小尺寸[8]Fig. 1 Contours of instantaneous streamwise velocity fluctuation at two xz planes (y+ = 55 and y+ = 275) representing the inner and outer layers. Panels (a-d) refer to single-phase flow with four decreasing domain sizes, respectively [8]
2 惯性粒子对壁面湍流的调制机理
当惯性粒子的浓度达到可以对流体相产生影响的时候,被调制的流体相将会反之影响粒子的分布与聚集[5]。在壁面湍流中,LSMs和VLSMs分别控制湍流内层和外层的流体动力学过程,因此我们将关注粒子对LSMs和VLSMs的调制机理[9-10]。为了突出粒子惯性的影响,在本节的计算中没有考虑重力的影响。
2.1 对LSMs的调制机理[9]
一般地,湍流调制依赖于粒子大小和湍流尺度的比值,同时依赖于粒子的响应时间尺度和流动特征时间尺度的比值。Gore[21]提出了用粒子与湍流积分尺度比来判断湍流抑制还是增强。Tanaka[22]提出了用流动“含能尺度”和粒子斯托克斯数构造的粒子动量数来预测湍流调制。尽管没有统一的机理来解释粒子的湍流调制过程,但在湍流内层中,小惯性粒子倾向于促进湍流、大惯性粒子倾向于抑制湍流,这个推论被广泛认可。我们通过研究粒子对近壁面拟续结构的调制作用,对其动力学演化过程进行细致分析,目标是尝试解释粒子对湍流的调制机理[9]。
在湍流内层,近壁面相干结构的演化是一个复杂的非线性过程,对其机理的研究一直持续到现在。其中Hamilton[23]提出的湍流自维持过程被广泛的用于研究LSMs的演化过程。Hamilton[23]应用了Jiménez[24]提出的最小湍流单元概念到平板Couette流动中,这样做的好处是可以控制展向计算域来孤立出一组大尺度条纹结构(large-scale streaks,LSS)和大尺度涡结构(large-scale vortex,LSV),这样就可以把注意力放在处于同一组自维持过程中的LSS和LSV的相互转换过程上,而不受处于其他组自维持过程中的LSS和LSV的影响,同时方便做能谱分析。而采用平板Couette流动来研究湍流自维持过程却不采用Poiseuille流动的好处是,在上下壁面之间只存在一组湍流自维持过程,即只存在一组LSS和LSV[28]。
图2展示了湍流自维持过程发生的位置及三种结构的演化过程。自维持过程发生于湍流内层中,包括三种结构:大尺度涡结构(LSV),大尺度条带结构(LSS),以及流向相关条带结构(x-dependent streaks)。三种结构之间的三个转换过程分别为:LSS形成,LSS分解,LSV再生。假设从LSV(流向不相关)开始,流体由于LSV的作用将流体“上扬”或“下扫”,形成了本地高速/低速的条纹结构LSS(流向不相关),而LSS是不稳定的,其失稳产生流向相关的条带,流向相关条带引入流向速度梯度(∂ux/∂x),其与流向涡量(ωx)相互作用,对应于涡量方程中的涡旋拉伸项,涡旋拉伸项的增加会促进LSV的生成,进而形成了一个完整的湍流自维持过程。应该说明对湍流自维持过程的研究是在谱空间中进行的,上述简单的物理描述相对应的数学表达式请参考文献[9,23]。

图2 壁面湍流的内外分区[25-26]以及自维持过程[23,27-28]. 在湍流Couette流动的最小单元中,右上的云图显示了“上扬”和“下扫”的LSS,向量图显示了一对旋转方向相反的LSV[9]Fig. 2 Sketch of various wall regions and boundary layers in wall units[25-26] and the regeneration cycle sub-steps[23,27-28]. In the top-right is the flow field in turbulent pCf(plane Couette flow) in miniunit. Large-scale vortex (LSV) is shown by vector fields and colored by scalar value of the streamwise vorticity. Large-scale streak (LSS) is shown by the contour of the streamwise velocity magnitude[9]
近三十年的研究证明湍流自维持过程可以被用来阐述近壁面LSMs的演化机理,因此我们[9]对粒子惯性及浓度对湍流自维持过程的调制进行了细致的研究,发现低惯性粒子(Stturb= 0.056,用LSV的周转时间尺度对粒子响应时间无量纲化)在LSV中的滞留时间更长,高惯性粒子(Stturb= 0.625)会比较均匀的分布在湍流场中。相对应的,低惯性粒子会促进湍流并缩短湍流自维持过程的周期,高惯性粒子会抑制湍流并增长湍流自维持过程的周期。由于低惯性(/高惯性)粒子的存在会增加(/减少)LSV的强度,导致近壁面湍流的增强(/减弱)。
以上,我们通过分析惯性粒子对湍流自维持过程的调制机理来研究粒子对近壁面大尺度结构的影响。然而在实际应用中,例如风沙流流动的雷诺数可以高达Reτ= O(106)[29],导致湍流的内层区间(y+<100)只占据了整个湍流空间的很小一部分(~100/Reτ),因此除了研究粒子对近壁面LSMs的调制机理,有必要研究更高雷诺数下惯性粒子对壁面湍流外层的调制过程。
2.2 对VLSMs的调制机理[10]
随着流动雷诺数的增加,实验中发现了湍流中的另外一种重要的特征结构,即超大尺寸结构(VLSMs)[30]。近年来由于直接数值模拟可以达到更高的雷诺数,VLSMs也成为了数值研究湍流方向的热点[31-33]。VLSMs的流向长度可以达到20倍壁面高度而且含有很高的能量,可以携带40%~65%的湍动能和30%~50%的雷诺应力[34-35]。由于高雷诺数湍流中外层占据大部分的空间,因此研究惯性粒子对VLSMs的影响有重要的应用价值,比如沙尘对大气近壁面层湍流的影响[2]。然而到目前为止,惯性粒子的湍流调制数值模拟研究还局限在相对小的雷诺数(Reτ< 300)和对湍流内层结构的研究,因此我们在文献[10]中研究了中等雷诺数(Reτ= 550,Reτ= 950)湍流中粒子惯性对VLSMs的影响。
图3展示了惯性粒子对VLSMs调制可能存在两个路径:1)直接路径,惯性粒子通过影响湍动能传输方程直接调制VLSMs;2)间接路径,惯性粒子通过调制湍流内层LSMs,进而调制湍流外层VLSMs。在谱空间里,直接路径代表惯性粒子直接调制与VLSMs同尺度的湍流结构,可以通过谱方法来分析湍动能传输方程进行研究;间接路径代表惯性粒子通过调制内层LSMs来达到调制外层VLSMs的目的。然而对于间接路径,目前LSMs和VLSMs的相互作用还尚有争论。一个观点是LSMs和VLSMs的形成是由不同的机理导致的,理由是Jiménez[25]发现了LSMs的自维持机理不需要VLSMs的参与,Hwang[31]通过大涡模拟的概念进行滤波测试,发现VLSMs可以在没有LSMs的存在时产生,Rawat[32]证明VLSMs也是一种自维持结构并且不从LSMs吸收能量;另一种观点是VLSMs和LSMs相互耦合存在,理由是文献[30,36]认为VLSMs并不是一种新的结构,而是由LSMs发展到湍流外层叠和而成,Toh[37]发现LSMs和VLSMs相互作用并彼此促进的周期过程,Lee[33]在湍流内层发现了能量反串的过程,即LSMs向VLSMs传递能量。
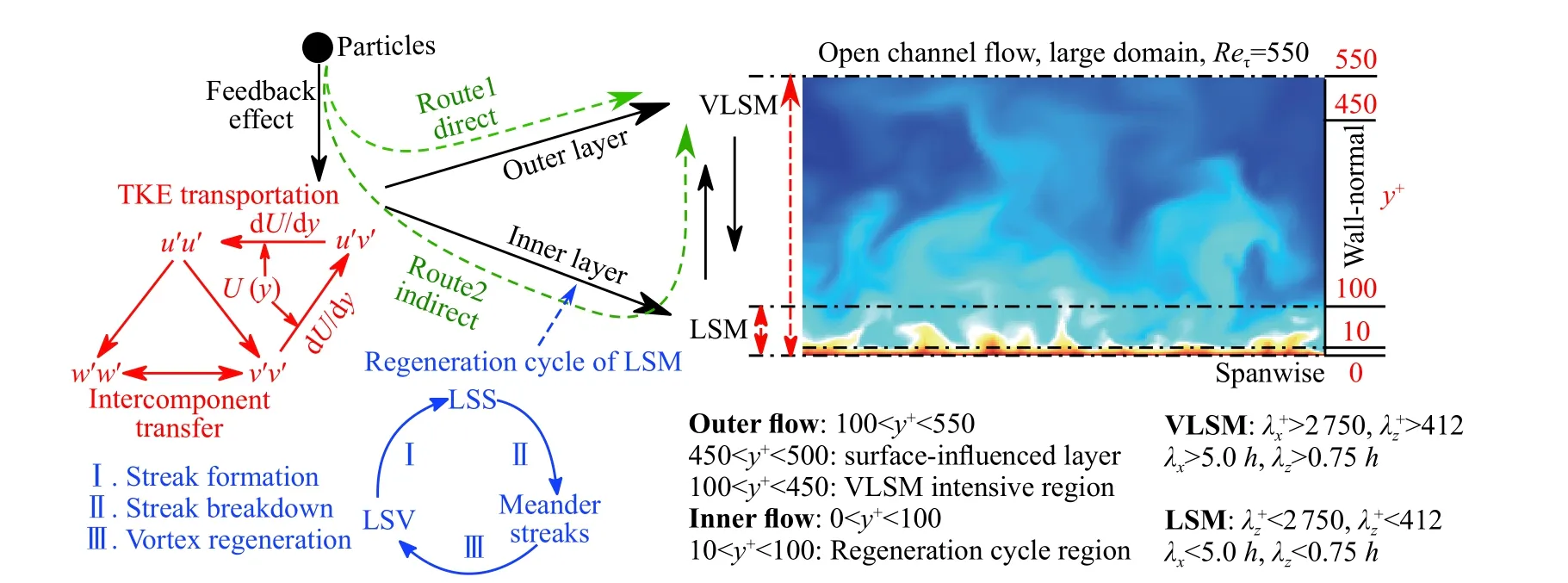
图3 惯性粒子调制VLSMs的两个路径,云图显示流向截面的瞬时速度,对应Reτ = 550的明渠流动[10]Fig. 3 Schematic of two routes of inertial particle effects on VLSMs through direct impact on turbulent kinetic energy transportation or via indirect upscale energy transfer from LSMs. On the right are streamwise velocity contours in the cross-stream plane of Reτ = 550 open channel flow and the flow region[10]
我们研究[10]发现VLSMs增加与粒子惯性之间的非单调变化关系,即小惯性粒子(St+= 2.42根据湍流内层时间尺度)和大惯性粒子(Stout= 6.0,8.2,根据湍流外层时间尺度)会增强VLSMs的强度(VLSMs强度通过计算预混谱中的双模态得到),然而中等惯性粒子对VLSMs的能谱几乎没有影响。为了验证上述提出的双路径调制VLSMs的假设,首先对小惯性粒子与大惯性粒子与流动的耦合进行人为控制,即:
(1)小惯性粒子与湍流内层双方向耦合,但与湍流外层单方向耦合;
(2)小惯性粒子与湍流内层单方向耦合,但与湍流外层双方向耦合;
(3)大惯性粒子与湍流内层双方向耦合,但与湍流外层单方向耦合;
(4)大惯性粒子与湍流内层单方向耦合,但与湍流外层双方向耦合。
测试结果为仅有(1)与(4)会增加VLSMs的强度。此测试说明,小惯性粒子促进VLSMs是通过其在湍流内层的反馈力,而大惯性粒子促进VLSMs是通过其在湍流外层的反馈力。进一步,用谱方法分析了雷诺应力输运方程,发现高惯性粒子对流体的反馈力作用于雷诺剪切应力输运方程,促进与VLSMs相同尺度的雷诺剪切应力的生成,雷诺剪切应力作用于流向湍动能输运方程而直接增加VLSMs的强度。物理解释为:VLSMs与高惯性粒子相互作用,粒子的反馈力促进与VLSMs尺度相同的“上扬”和“下扫”流动,随后这些超大尺度的“上扬”和“下扫”结构从平均流动中吸收能量,最终直接促进同等尺度VLSMs的生成;低惯性粒子增强湍流自维持过程[9]并增加LSMs的强度,通过能量反向级串,最终促进VLSMs的生成。这种间接调制机理,即小粒子通过调制LSMs并最终调制VLSMs,支持了上述的第二种观点[30,33,36-37]。
以上讨论了惯性粒子的存在对LSMs和VLSMs的调制机理,除了粒子对流场的影响以外,研究粒子在LSMs和VLSMs的聚集状态也对大涡模拟粒子流的准确性及局限性提供借鉴意义。由于计算能力的限制,目前直接数值模拟耦合大量的惯性粒子(O(108))只能达到中等的雷诺数(Reτ<1 000),远远不能达到实际情况中的超高雷诺数Reτ~O(106)。在高雷诺数的情况下,由于大涡模拟过滤掉小于计算网格的流动结构,导致计算中得到的粒子本地处的流体速度并不精确(即滑移速度不准确),Marchioli[38]发现即使是在低雷诺数Reτ= 180的情况下,大涡模拟也会低估粒子近壁面的聚集,同时粒子的群聚形态也不同于直接数值模拟。而在高雷诺数的情况下,采用大涡模拟往往只能捕捉到VLSMs而过滤掉LSMs,想要准确地应用大涡模拟到高雷诺数湍流粒子流中[39-40],有必要衡量这两种重要流动特征结构对不同惯性的粒子分布的影响。
3 粒子在LSMs及VLSMs中的聚集与
采用了如下的策略来应用直接数值模拟分离LSMs与VLSMs对粒子的影响:
(1)应用截断计算空间的方法分离出LSMs,比较粒子分布在只有LSMs及在同时有LSMs和VLSMs时的不同,见图1;
(2)在计算过程中过程中,在谱空间分离出LSMs和VLSMs,人为的控制粒子与这两种结构流场的耦合,比较粒子分布在只有VLSMs及同时有LSMs和VLSMs时的不同,见图4。

图4 Reτ = 550单相流,y+ = 100水平截面以及四个边界截面的瞬时流向脉动速度云图,“+”代表依据黏性尺度进行无量纲化[11]Fig. 4 Instantaneous contours of streamwise velocity fluctuation on a wall-parallel plane at y+ = 100(and domain boundary walls) in single-phase flow,normalized by uτ[11]
对于测试(1),在第1.3节中已经介绍了四种计算域尺寸对粒子的影响,重点关注粒子的一阶与二阶稳态[8]。本节用截断计算域作为一种分离LSMs的方法,关注VLSMs的存在对粒子分布的影响。首先根据文献[41],选择计算域流向尺寸足够大到包含一个LSMs并足够小到排除外层VLSMs对内层LSMs的影响,在Reτ= 550时,我们选择截断计算域尺寸为Lx+= 1 375、Lz+= 825,而大尺寸计算域尺寸为Lx+=10 367、Lz+= 3 456,通过比较二维空间的预混谱,截断计算域得到的湍流内层能量谱与大尺寸计算域以及文献[42]的结果几乎吻合,但湍流外层的能量谱由于截断域的影响,小尺寸计算域由于尺寸太小显然捕捉不到能量谱的双模态形式。在加入惯性粒子(低惯性St+= 24.2和高惯性St+= 182)以后:一方面,在湍流内层尤其是接近壁面处,粒子的浓度小于大尺寸计算域接近20%,这归因于外层VLSMs的存在增强了湍流湍泳(由于脉动速度在壁面垂直方向梯度诱导的粒子运动,粒子趋向于向湍流度弱的方向移动),由于粒子的平均浓度在两种计算域中保持相同,因此截断域的湍流外层粒子浓度则小于大计算域中的粒子浓度;另一方面,我们通过冯洛诺伊图来计算粒子在壁面垂直方向上的群聚形态[43],发现无论对低或高惯性粒子,截断域总是趋向于低估粒子的群聚效应,尤其是在湍流外层区域(y+< 100),这同样归因于外层VLSMs的影响。
对于测试(2),在计算过程中我们人为的控制粒子与流场特定结构的耦合,具体的步骤为:将速度场变换到谱空间,将流场分为LSMs和VLSMs两部分,再从谱空间变换到速度场(见图4),粒子只与LSMs或VLSMs对应的速度场耦合,这种人为控制的粒子-流场耦合在计算的每一步都进行一次,因此计算时间较长。通过以上方式可以得到三种粒子分布,即全流场下、LSMs流场下、VLSMs流场下的粒子分布(见图5),可以看到对于小惯性粒子,其粒子群聚主要发生在湍流内层,直观上LSMs流场下粒子湍流内层的群聚看起来与全模拟相似(图5(a)与(c)比较)。而在湍流外层,由于其响应时间尺度远小于特征结构VLSMs的时间尺度,因此小惯性粒子在湍流外层中趋向于无惯性粒子;对于高惯性粒子,由于其响应时间尺度与VLSMs的特征尺度相当,因此高惯性粒子的群聚发生于湍流外层,然而即使是直观上,VLSMs流场下的粒子在湍流外层的群聚形态也和全模拟相差很大(图5(b)与(d)比较)。随后对粒子聚集(粒子浓度曲线)以及粒子群聚(冯洛诺伊图计算)进行了比较,发现在湍流内层,LSMs流场会低估惯性粒子的浓度,在湍流外层,VLSMs流场可以得到和全流场相近的惯性粒子的浓度。对于粒子群聚现象,LSMs流场结果更接近于全流场结果,而VLSMs流场结果与全流场结果相差很大。
根据测试(1)与测试(2),发现LSMs影响粒子的聚集并控制粒子的群聚。在大涡模拟粒子流中,过滤掉LSMs可以估计湍流外层的粒子浓度,但会低估湍流内层的粒子浓度。大涡模拟捕捉不到正确的粒子群聚,导致粒子与流场的双向耦合作用到不合适的流场结构中,因此不适宜采用大涡模拟和粒子的双向耦合研究粒子的反馈作用对流场的调制。

图5 粒子在三种流场中的分布[11]Fig. 5 Instantaneous snapshots of particle locations (black dots)[11]
4 影响粒子沉积的机理研究[12-13]
在一些地球物理相关测量中,能准确估算雪、雨、沙尘等的表面沉积速率对研究降水量、土地沙化、城市污染有重要的实际应用价值[44-45]。这些粒子的沉积过程,可以看作惯性粒子在重力作用下穿越壁面湍流场到达壁面这个简化的物理过程。当粒子的St+~0时,粒子可以近似看做具有沉降速度的被动标量,Rouse[46]推导出了用于预测粒子垂直浓度的幂定律,幂指数与惯性粒子的斯托克斯沉积速度成一定比例,被广泛应用于地球物理的相关研究中。然而对于惯性粒子,文献[46]给出的幂定律则不再适用,Richter[47]尝试加入粒子对流速度的一阶展开(见文献[48])去修改幂定律,通过与直接数值模拟结果比较,发现这样考虑粒子惯性效应的一阶修正只使用于St+<<1的情况,对于St+>1的惯性粒子,目前存在的理论模型仍然很难准确预测粒子的垂直浓度。对于惯性粒子,文献[46]结论不适用的原因是其假设粒子在湍流场中均匀分布、粒子的沉积速度等于其斯托克斯沉积速度,这样的假设对于St+>1的惯性粒子不再适用,因为即使在均匀一致湍流中,由于惯性粒子趋向于远离涡的中心,粒子倾向于被涡旋转向重力方向加速,导致惯性粒子的沉降速度大于其斯托克斯沉积速度[49-50]。而在壁面湍流中,由于多种湍流尺度的存在,不同惯性的粒子会偏向聚集于湍流场的不同结构中,影响粒子加速的因素变得更加复杂。
在文献[12-13]中,我们首先通过推导相空间下的概率密度分布的主方程(phase-space master PDF equation)得到了控制粒子稳态的输运方程,进而推导出控制粒子沉降速度的方程(数学推导过程请参考文献[12,51]):

其中vp(t) 为粒子的沉降速度,y为壁面垂直方向,ρ为边〈缘概率密度函〉 数用来描述粒子的空间分布,S=(vp(t)-〈vp(t)〉)2为粒子脉动速度的协方差,up(t)为粒子处的流体速度。通过对此控制方程的分析,发现粒子的沉降速度是由如下五个因素来控制,对应方程右侧由左至右依次为:粒子加速项,粒子扩散项,湍流湍泳项,粒子本地流场速度项以及重力加速项。对上述五个因素的物理描述为:粒子加速项是由粒子在壁面垂直方向的速度梯度导致的,粒子扩散项是由粒子在壁面垂直方向的浓度梯度导致的,粒子本地流场速度项是由粒子在湍流中的偏向聚集现象导致的,重力加速项是由外力导致的。随后通过直接数值模拟计算了上述五个因素在零粒子通量以及有限大小粒子通量两种情况下对粒子沉降速度的贡献。进一步的,我们讨论了扩展文献[46]中的模型从St+~0粒子到St+> 1粒子的可能性,发现模型中的不封闭项包括由于粒子聚集导致的漂移系数以及粒子壁面垂直方向的湍动能。我们目前仍然尚无法提出满意的模型用来预测St+> 1惯性粒子的壁面垂直方向的浓度曲线,这将是未来要开展的工作之一。
5 结 论
本文应用直接数值模拟耦合拉格朗日点粒子这种相对简单的数值模型,对惯性粒子和壁面湍流这个复杂且具有重要实际应用的问题开展了一些相关研究。重点关注的物理问题是粒子对壁面湍流的调制,以及粒子在两种特征湍流结构中的分布以及粒子的沉积速度。在未来的研究中,将继续尝试建模预测粒子垂向浓度曲线,热对流效应对壁面湍流及粒子分布的影响,粒子在复杂流场结构中的运动(例如旋转湍流),带电/磁粒子在壁面湍流中的运动,以及应用大涡模拟技术研究复杂地形下粒子分布等相关研究工作。
致谢:本文涉及到的工作是作者在美国圣母大学的研究内容,全部已公开发表到经过同行评审的专业期刊或尚未经过同行评审的预印版。本工作得益于美国陆军研究实验室以及海军研究办公室的项目支持,计算资源来自于高性能计算现代化项目(HPCMP)以及圣母大学研究计算中心。相关的研究工作得益于几位合作者的贡献:美国圣母大学的Hyungwon John Park博士以及David H. Richter副教授,美国杜克大学的Andrew Bragg助理教授,美国明尼苏达大学的Kee Onn Fong博士以及Filippo Coletti副教授(现工作于苏黎世联邦理工大学),美国密歇根大学的Jesse Capecelatro助理教授。感谢几位优秀学者访问本人所在的美国圣母大学课题组时所提出的宝贵建议:美国加州大学洛杉矶分校的Marcelo Chamecki教授以及美国华盛顿大学的James J.Riley教授。感谢已发表论文和本论文匿名审稿人提出的宝贵建议。最后感谢相关专家的推荐及《空气动力学学报》编辑部的邀请。

