基于核密度波动的异常检测算法

张博文，刘 智，桑国明

大连海事大学 信息科学技术学院，辽宁 大连116026

异常检测的目的是找出那些不同于预期的数据点，并尝试找出与大多数数据表现模式有显著差异的异常模式。异常检测应用的领域包括：欺诈识别、故障诊断、异常基因检测等[1]。

在实际检测任务中，异常标签的获取往往需要花费极大的成本，异常检测任务面对的待检测数据往往是无标签数据。因此设计科学有效的无监督异常检测算法具有重要意义。

基于密度的方法是一类重要的无监督异常检测算法。它们更注重考虑数据分布从紧密到稀疏变化的位置、采用直方图、k-邻域等方法完成对数据空间的分割，提高了检测结果的可解释性。Breunig等人提出的LOF算法[2]，Papadimitriou提出LOCI算法[3]和Kriegel等人提出的LoOP算法[4]通过考察数据点局部密度的稀疏程度判断该点是否为异常点；Tang等人引入链式距离的概念，进而提出了COF算法[5]；Jin等人提出的INFLO算法[6]在计算近邻密度时考虑了k近邻和反近邻。Goldstein等提出的HBOS[7]方法构造基于频率直方图的概率密度来计算异常评分。赵晓永等人[8]提出基于主动学习的离群点集成挖掘方法，以基于统计和相似度的方法为基学习器。Lin等人[9]成功运用三种基于密度的异常检测算法应用于卒中数据。

核密度估计是一种常用非参数统计模型，是从数据本身出发，对数据特征和分布进行描述。Xu等人[10]运用核密度估计方法获得对交通流量数据最优估计的概率密度函数，然后建立信念函数来检测数据中的异常值。Latecki[11]为克服数据点间的欧式距离过小导致的密度估计值较大的情况，运用局部密度估计代替欧氏距离计算密度估计值。这些方法的研究与应用足以证明核密度估计方法在异常检测领域的优越性。

在基于核密度估计的异常检测算法中，常常认为异常点具有相对较低的核密度，而这一假设并不总是正确的。正常点的核密度也可能较低。因此近年来有学者提出有关密度波动的异常检测算法，其主要思想是异常点密度变化情况更复杂，波动变化大。Cao等人[12]提出一种基于核邻域密度变化的异常值检测算法，该算法运用核函数将数据集中的对象映射到高维空间内，在单位距离内点的个数定义数据对象的核邻域密度。比较一点与其邻域内的数据点近邻核密度的平均密度波动情况。Waid等人[13]提出了一种KDOF算法，通过计算比较数据点间的相对核密度值波动来确定数据集中的异常点。这些算法采用了一种更通用的特征表达方式，然而同样只是专注在局部范围内的检测，对全局异常点和集体异常检测能力较弱。此外近邻类算法常常敏感于近邻参数k的取值。

针对上述问题，本文提出一种鲁棒的基于核密度波动的KDF（Kernel-Density Fluctuation factor）异常检测算法。充分利用核密度估计的优势，结合密度波动思想，定义了核密度波动因子KDF。在此基础上进一步制定了检测规则，在生成数据集和真实数据集中均可以提供准确且稳定的异常检测性能。

1 KDF异常检测算法原理

本文首先运用t-SNE算法对数据集进行特征提取，降低维数的同时保持数据原有的结构。然后创新性地提出可以综合考虑邻域内和邻域外的密度波动的核密度波动因子KDF，据此检测数据集中的异常点。

文中的核密度估计函数选取了使用较多的多元高斯核，如公式（1）：

(X1,X2,…,X n)为n个d维样本，多元高斯核函数为：

对于任意正整数k，数据点P的k-近邻距离表示为d k(P)。d k(P)必须同时满足以下两个条件：

（1）数据集D中至少存在k个数据点Q∈D{P}满足d(P,Q)≤d k(P)。

（2）数据集D中至多存在k-1个数据点Q∈D{P}满足d(P,Q)＜d k(P)。

其中{P,Q}∈D,d(P,Q)为数据集D中数据点P和Q间的直达距离。这里距离使用Euclidean距离，即有对于d维空间上的数据点P=(p1,p2,…,pd)，数据点

数据点P的k-近邻区域N k(P)={Q|d(P,Q)≤d k(P),Q∈D{P}}。|N k(P)|表示数据点P的k-近邻区域N k(P)中的元素个数。

定义1绝对核密度波动因子AKDF（Absolute Kernel-Density Fluctuation factor），如公式（2）：

对于数据集合N和数据点P的k-近邻内的数据点集合N k(P)，运用集合内的点估计出P点的核密度值ρ(P)：

运用k-近邻以外的数据点and，估计出的P点的核密度值ρ′(P)：

定义的AKDF刻画了数据点的全局特征和集体特征。ρ(P)主要描述了数据点P周围的局部密度特征。核密度估计过程易受极端值影响，因此在计算ρ′(P)时，用内的点对其进行估算。

为方便数据可视化，本文运用二维的生成数据，分别对两个变量进行一维核密度估计及可视化，其结果如图1所示。以数据中一异常点的k-近邻区域边界为分界，将数据化分为两部分，分别对其进行核密度估计。两部分的核密度估计曲线如图2。

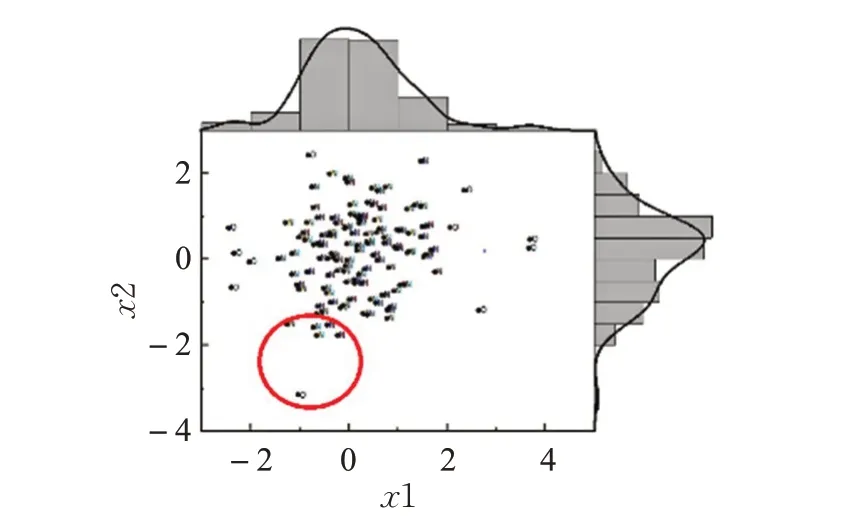
图1 二维生成数据核密度估计曲线

图2 数据核密度估计曲线

如图2异常点N k(P)内的数据点的核密度估计曲线和中的数据点的核密度估计曲线存在较大差异。因此(ρ(P)-ρ′(P))2越大，P点越可能是异常点。AKDF考虑了数据点所在局部区域与全局的关系，所以具有较好的区分能力。同时这一计算方法平衡了近邻参数k的选择问题，保证核密度估计效果的同时可以识别局部异常点，减少调优空间。

目前常用异常检测算法都着重于发现异常类型中的“点异常”，而当异常点聚集成一个簇时，这种聚类异常难以被发现。考虑到已有算法对集体异常点发现能力不足的问题，提出的AKDF可以很好地描述集体异常点的特征。若点P及N k(P)内的点均为异常点，即存在集体异常。此时ρ(P)较大，ρ′(P)较小，同样有(ρ(P)-ρ′(P))2较大。

定义2相对核密度波动因子RKDF(P)（Relative Kernel-Density Fluctuation factor），见公式（5）：

定义的RKDF主要用来度量数据点P与其k-近邻内数据点的核密度值的差异情况。RKDF(P)越大，P点越可能是异常点。相对核密度波动因子充分考虑了异常点和正常点之间、正常点和正常点之间的关系。数据集内常常具有几个集群，不同数据集群的核密度曲线可能存在差异，所以运用数据点的k-近邻内的点而不是全部样本点进行核密度估计。

定义3核密度波动因子KDF(P)，如公式（6）：

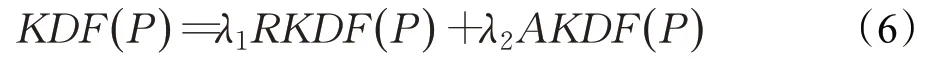
KDF综合考虑数据点的局部和全局异常特征、点异常特征和集体异常特征，将RKDF和AKDF进行线性组合运算。λ1和λ2为相应权重，满足λ1+λ2=1。在实际应用中，可以根据数据特点设置相应的权值，平衡局部特征、全局特征和集体特征间的关系，尽可能从多个角度发现潜在异常点。计算所得的KDF值越大，数据点为异常点的可能性越大。

2 KDF算法伪代码

算法1 KDF算法

输入：待测样本的数据集合D，带宽h，近邻参数k

输出：异常因子得分（KDFS），异常点集合O

1.对数据集D进行t-sne降维，D′=t-sne(D)

2.for each pointPinD′,do

5.计算AKDF(P)；

6.end for

7.for each pointPinD′,do

8.计算RKDF(P|ρNk)(ρNk={ρ(Qi|N k(Q i))|QiϵN k(P)})；

9.计算KDF(P)；

10.end for

11.for each pointPinD′,do

13.输出异常得分KDFS(P)

14.ifKDFS(P)＞1：

15.点P进入异常点集合O；

16.end if

17.end for

18.输出异常点集合O

3 算法分析

3.1 参数稳定性分析

无监督异常检测算法存在调优困难的问题，因此异常检测算法的稳定性是算法分析中的一个重要因素。

3.1.1 近邻参数k

近邻参数k是近邻学习的重要参数。近邻算法常常敏感于k值的选择。当k取值较小时，近似误差减小，模型变得复杂，估计误差增大，容易发生过拟合；选取的k值较大时，模型变得简单，估计误差会减小，近似误差会增大，容易发生欠拟合。KDF算法同时考虑了数据点邻域内外的核密度值差异，在理论上可以减小算法对近邻参数k的敏感性。

3.1.2 核密度估计带宽h

核函数中带宽参数h是一个关键的超参数，用于控制模型的平滑程度。h值越大，则得到的概率密度曲线就越平滑。当样本数据已知时，f̂h(x)的精度如何取决于核函数和带宽h的选择。f̂h(x)依概率收敛于f(x)。多数情况用核密度估计偏差和核密度估计方差来衡量其估计效果。核密度估计的偏差（记为和核密度估计的方差（记为）计算公式如下：

由计算核密度估计偏差和核密度估计方差公式可知若h取值过大，则偏差增大，方差降低，导致f̂h(x)过于平滑，密度函数f(x)的某些特征被掩盖；若h取值过小，则偏差减小，方差增加，导致f̂h(x)出现较大波动，无法选择相应的带宽h值使偏差和方差同时减小[14]。

在KDF算法中，将数据点与其邻域内点的KDF进行比较计算，尽可能弱化不同h值对最终检测结果带来的影响。

3.2 算法时间复杂度分析

由于涉及对每个点k-近邻区域的搜索，为提高k-近邻的搜索效率，可以考虑使用Kd树的结构存储训练数据，以减少计算距离的次数。对于n个样本，建立Kd树后算法的时间复杂度达到O(2nlbn)。

4 实验结果与结果分析

4.1 实验数据集

为验证KDF算法的性能，在生成数据集和真实数据集上进行了实验。生成数据集中正常样本点服从二维标准正态分布，异常点数据一个维度服从参数为（2，0.5）的伽马分布，另一个维度为服从参数为1.5的指数分布。选取的真实数据集为Wine数据集和Banknote数据集。Wine数据集中，类别3视为异常点类。Banknote数据集中，类别1视为异常点类；实验数据集的详细信息描述如表1所示。

表1 实验数据集信息表

4.2 实验设计

实验中的对比算法包括LOF算法[2]、KNN算法[15]、LOCI算法[3]和KDOF算法[13]。算法中权重设置为λ1=λ2=0.5。

在与其他算法进行结果的比较时，确定KDOF算法和KDF算法中计算核密度估计的带宽h，比较不同近邻参数k下不同算法的性能。在对参数h的敏感性分析中，固定了近邻参数k，考虑带宽h的变化对最终实验结果的影响。

4.3 评价指标

本文运用了两个模型性能评价指标[16]，从不同角度评价算法的性能。

4.3.1 基于异常评分的排序准确率

无监督异常检测算法往往对最为异常的一部分数据进行报警。对数据点所得的异常评分KDFS（Kernel-Density Fluctuation factor Score）进行降序排序，选择前5、10、20个点计算其检测准确率。这一指标可以度量算法所得异常评分的合理性，同时又减少单纯计算准确率对判决阈值的依赖。

4.3.2 F1值

在异常检测任务中，既要尽可能检测出全部的异常情况，又要尽可能减少“误检”产生的多余成本。因此本文运用F1值作为异常检测算法性能的度量。

4.4 实验结果

实验算法中近邻参数k=10，KDF算法和KDOF算法中核密度估计带宽h=0.5。

从表2中可以看出，KDF算法在三个实验数据集均取得了很好的结果，排序准确率在大多数情况下明显高于其他对比算法。运用定义的KDF来检测数据集中的异常点具有科学性。

表2 算法异常得分排序准确率比较表

如图3所示，在三个实验数据集上，KDF算法的F1值均高于其他对比算法。实验结果说明提出的方法可以更全面准确地检测异常点。

图3 不同算法的F1值比较

4.5 参数的敏感性分析

4.5.1 近邻参数k

对算法在不同k值下，在三个数据集中得到的F1值取平均值，与对比算法结果进行比较。

由图4（a）图中可以看出在k取值较小时，不同取值下的KDF算法F1值均高于其他对比算法。而且KDF算法选择不同的近邻参数k对算法检测结果影响较小，KDF算法对于k的选择表现出了良好的鲁棒性。

4.5.2 带宽h

本文通过设置不同的带宽h值，对比KDF算法与KDOF算法在三个数据集上F1的平均值。

图4（b）图中显示：和KDOF算法相比，KDF算法在数据集中计算得到的F1值未出现明显波动。h值的变动并不会给最终的检测结果带来较大的影响。因此算法可以提供稳定的检测结果。

5 结束语

图4 参数敏感性分析比较图

本文提出了一种基于核密度波动的异常检测算法。KDF算法具有很多优势：首先，运用核密度波动特征代替密度特征识别异常点。这一特征考虑异常点之间、异常点与正常点之间的特征关系，可以更好地描述数据中的动态特征。其次，定义了核密度波动因子概念，充分考虑数据点的局部特征和全局特征。经过理论分析和实验结果分析表明：KDF算法具有更稳定和准确的检测性能。在无监督异常检测任务中，有较好的应用前景。未来将考虑进一步扩展KDF算法，使其更适用于高维大规模数据中。