基于自适应卡尔曼滤波的Meanshift跟踪算法

陈 薇，袁文定，方 强，李 海，项奇清

（合肥工业大学 电气与自动化工程学院，合肥 230009）

0 引言

在视觉跟踪中，一般来说可以将目标跟踪算法分为4类[1]。第一类是基于目标区域匹配的跟踪算法；第二类是基于目标运动特性的跟踪算法，如卡尔曼滤波、粒子滤波算法；第三类是基于目标模型的跟踪算法，如Snake模型、3D模型；最后一类是基于目标特征匹配的跟踪算法，如Meanshift、Camshift算法。在实际应用中Meanshift算法[2,3]以其计算量小、快速匹配等特点被广泛的应用。文献[4]采用Meanshift算法，在视频环境良好的情况下，实现了对运动目标的准确跟踪。文献[5,6]针对目标背景复杂噪声较大的情况，在使用Meanshift算法的基础上，通过结合纹理特征解决了跟踪算法在目标存在背景干扰，目标跟踪不准确的问题，实现了对目标的准确跟踪。文献[7,8]在使用Meanshift算法的过程中有效的结合了卡尔曼滤波，提出了一种基于卡尔曼滤波的Meanshift算法（KF-Meanshift），解决了在跟踪目标被遮挡或者视频背景序列存在较大噪声、目标与背景颜色相近时跟踪的问题，进一步提升了Meanshift算法的性能，使得该算法的应用场合多样化。

KF-Meanshift算法对初值较敏感，当选取的初值存在一定偏差时，滤波结果将存在明显偏差，从而导致滤波发散，同时该算法对系统数学模型及噪声先验信息存在高度的依赖性，当不能准确地确定系统模型和噪声统计特性时，就会使滤波效果失去最优性或者发散。为了解决上述问题，本文提出一种AKF-Meanshift算法，在系统噪声未知的前提下，实现对有遮挡情况的目标的跟踪，同时在视频序列出现较大噪声干扰的情况下，完成对目标的跟踪。

1 自适应卡尔曼滤波

1.1 跟踪目标运动模型

在实时的跟踪视频序列中，由于相邻帧图像的时间间隔很短，因此在建立模型时可以认为目标在相邻两帧的运动的匀速的[9]。

系统状态方程为：

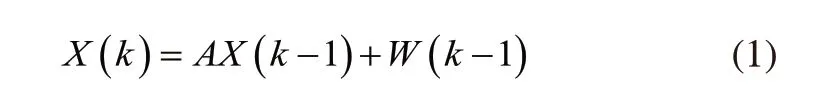
系统观测方程为：

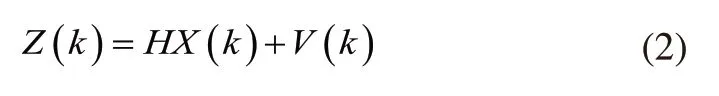
在本文中k为视频处理序列的当前帧数；X（k）为第k帧的跟踪目标的状态估计值；Z（k）为第k帧的跟踪目标的量测值；A为状态转移矩阵；H为观测矩阵；W（k）为过程噪声矩阵；V（k）为系统观测噪声；过程噪声协方差矩阵为Q，观测噪声协方差矩阵为R。

由运动模型可知：

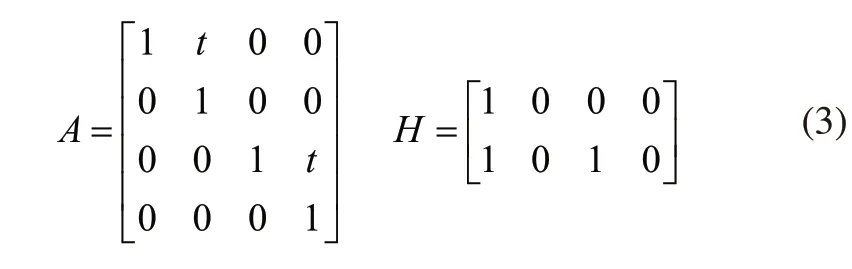
式中，t表示相邻两帧时间间隔。

1.2 卡尔曼滤波

卡尔曼滤波器包括两个阶段：预测阶段和更新阶段，在预测阶段，卡尔曼滤波器通过使用上一状态的估计，对当前状态进行估计。在更新阶段，滤波器通过预测出的状态值，对系统进行更新。

预测阶段：

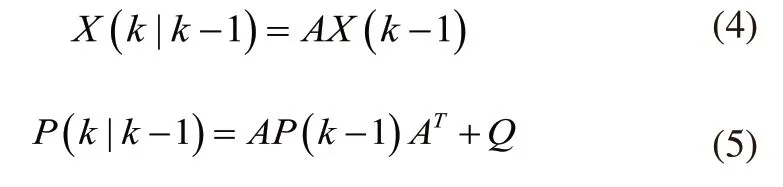
式中P（k）为状态协方差矩阵。

更新阶段：

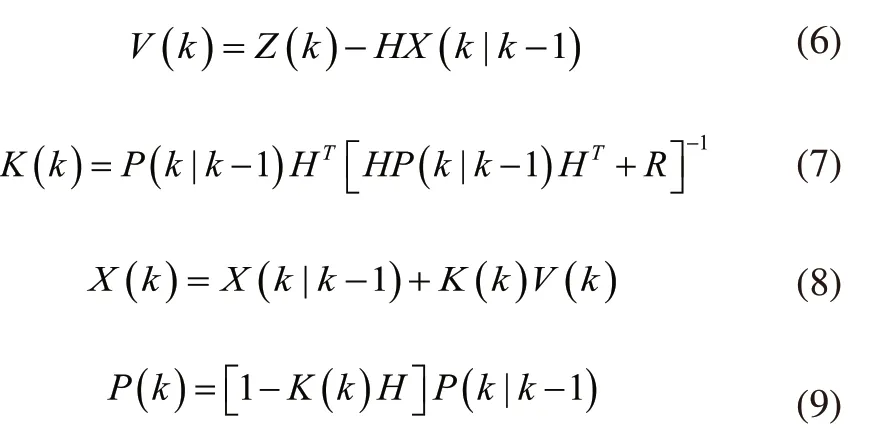
式中K（k）为卡尔曼滤波增益。

1.3 改进的自适应卡尔曼滤波

1.3.1 渐消因子

在卡尔曼滤波的基础上引入渐消因子[10]，组成具有强跟踪效应的滤波器，通过调整预测误差值，从而加大当前观测量的权重，减小算法初值偏差带来的影响，抑制滤波的发散。这种算法与传统的KF算法主要不同之处在于把式(5)中引入渐消因子λ（k），使得式(5)变成式(10)。

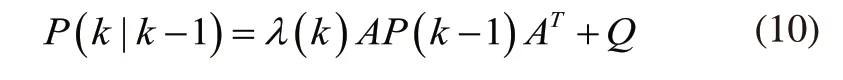
为了减小非线性规划求最优渐消因子的计算量，这里给出一种λ（k）的次优算法。

次优渐消因子：

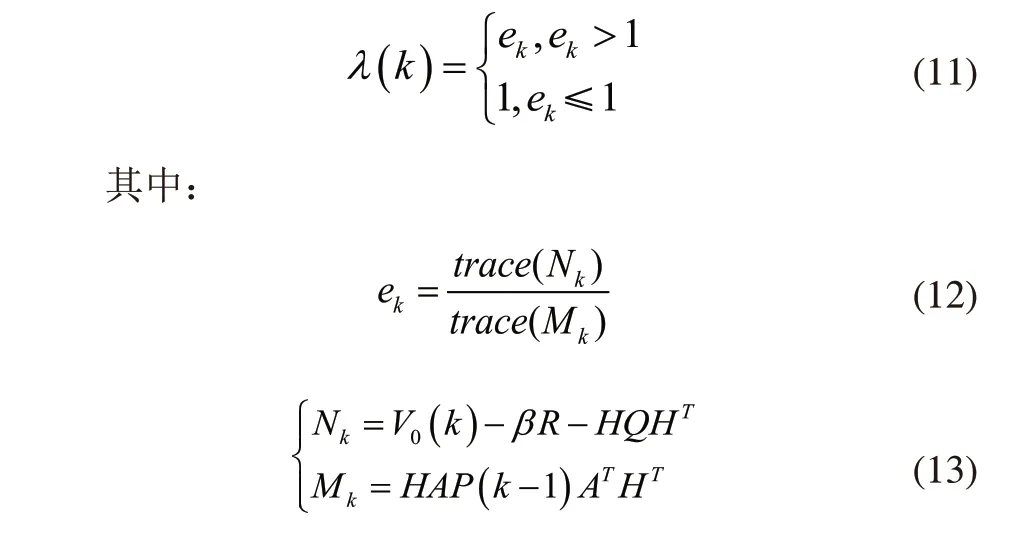
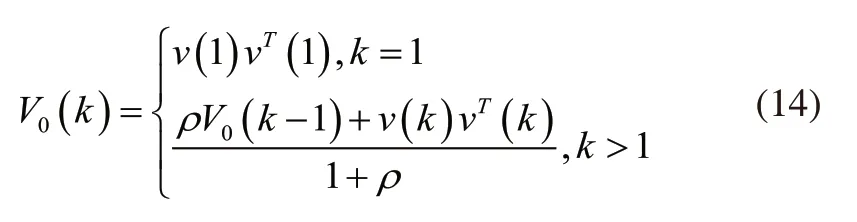
式中V0（k）为残差协方阵；ρ为遗忘因子，这里ρ=0.95；β为弱化因子，一般情况下，取β≥1。

1.3.2 遗忘因子

传统的KF算法的系统噪声会影响滤波结果，通过引入遗忘因子[11]，在滤波过程中更新系统噪声从而使得模型更加准确。测量噪声协方差估计为：

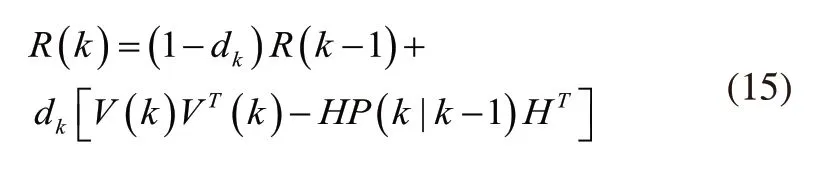
式中，加权系数dk=（1-b）/（1-bk+1），其中b是遗忘因子，0＜b＜1，其取值范围为0.95～0.995。

在滤波过程中，如果滤波出现收敛的趋势，误差协方差矩阵P会逐渐减小到0，同时因为观测矩阵H为定值，那么测量噪声协方差可由式(15)改为式(16)：

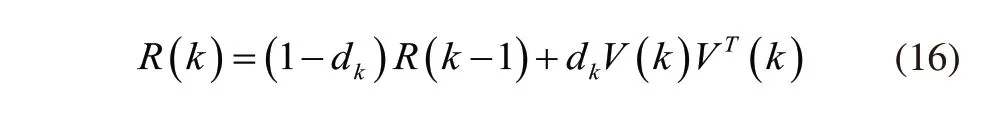
状态估计协方差更新矩阵由式(9)变成式(17)：

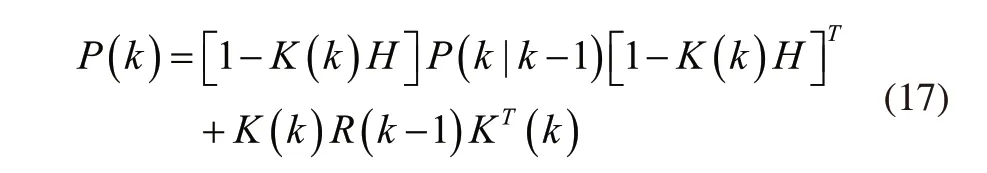
1.3.3 抗差处理

通过引入遗忘因子一定程度上提升了系统的鲁棒性，但在实际应用中观测向量不可避免地会出现粗差，该方法并不能去除测量值的粗差，若在数据处理过程中不对这些粗差进行处理，会使滤波估计极不可靠。在卡尔曼滤波算法中，对于野值的判别可以引入“新息”的概念[12]。

系统新息为：

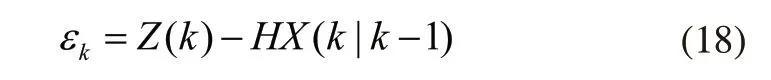
式中，r是（M×1）维的向量，M为观测值的维数，其表示可接受的极限误差，一般取4～6。

若系统中出现粗差，则需将观测模型的量测噪声方差用等价方差替换，这里采用IGGⅢ函数方法构建等价方差：

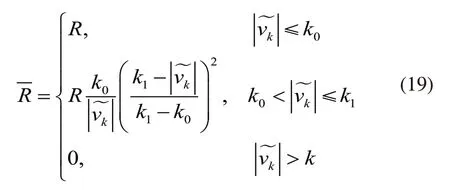
式中，k0，k1分别为正常界和淘汰界的取值，一般取k0=1.0～1.5，k1=2.0～3.5；为预测残差统计量。

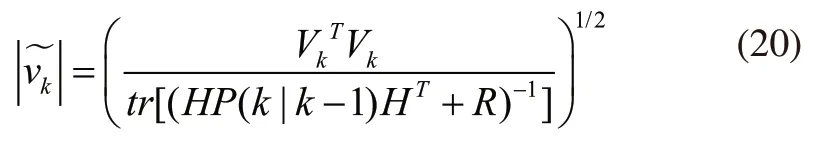
那么式(7)改为式(21)：

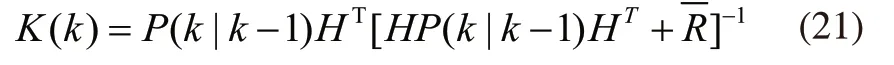
2 基于自适应卡尔曼滤波的Meanshift跟踪算法

在第1节中，本文阐明了传统卡尔曼滤波的不足，导致预测结果的不理想，之后，本文给出了一种解决办法：采用一种自适应卡尔曼滤波，来实现在系统噪声未知情况下构建一个作用良好的滤波器。将自适应卡尔曼滤波和运动目标跟踪算法结合，使得运动目标的跟踪更加准确。

2.1 目标检测

传统的跟踪算法需要手动确定跟踪目标的搜索窗口大小，为了进一步提升算法的便捷性，本文采用一种三帧差分法，实现对跟踪目标的检测。该算法通过选取视频序列中连续的三个帧，在进行平滑处理后分别进行帧差分处理。第k帧图像中减去第k-1帧图像从而获得二值图像D1，第k-1帧图像减去第k-2帧图像从而获得D2。最后，通过与操作得到图像D，从而检测到运动目标的位置。

2.2 Meanshift算法

Meanshift算法通过加权概率密度函数q={qu}来对目标模型进行描述。目标模型概率密度函数计算如下：

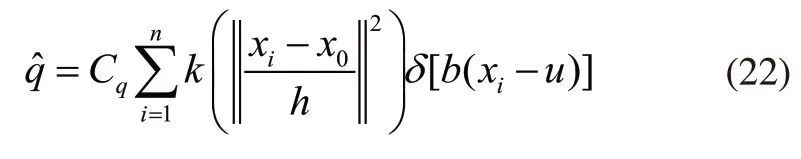
式中，i∈[1，…，n]，n表示像素点的个数，u∈[1，…，m]，m表示特征值总个数。Cq是目标模型一个标准化的常量系数，k（x）为核函数的轮廓函数，h表示决定权重分布的核函数窗口大小，x0为目标窗口中心的坐标向量，xi为目标窗口内任意点的坐标向量，δ（x）表示Delta函数。

在跟踪序列的某一帧中，假设候选目标在以y0为中心的搜索窗口内，则候选目标的概率密度函数计算 如下：

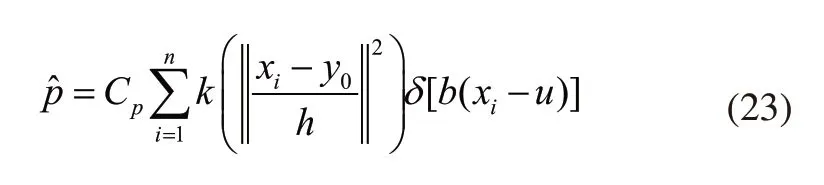
在目标跟踪中，通过引入Bhattacharyya系数来判断目标模型和候选目标模型的相似程度。通过相似系数η来描述目标模型和候选目标模型的相似度，η值在0～1之间，其值越大，则两个模型越相似。这里相似系数采用Bhattacharyya系数：

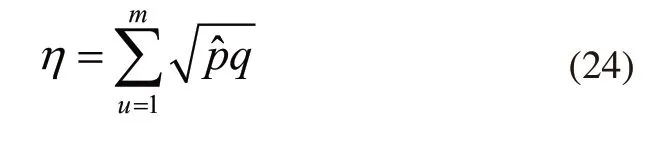
式中，u∈[1，…，m]，m表示特征值总个数。

2.3 AKF-Meanshift跟踪算法步骤

本文的算法流程如下：

Step1：对相关算法进行初始化，确定算法参数，同时根据根据式(4)～式(21)，建立自适应卡尔曼滤波模型。

Step2：利用三帧差分法确定跟踪目标，求出检索目标区域，并计算颜色直方图，根据式(22)建立目标模型。

Step3：利用初始化后的自适应卡尔曼滤波器对当前帧的目标候选区域进行预测，得到当前帧目标迭代的初始位置y0。

Step4：把y0作为Meanshift算法迭代的起始位置，在以y0为中心的区域对目标开始进行搜索，根据式(23)计算出候选目标模型。

Step5：根据式(24)计算模型的相似度系数。

Step6：把y0代入Meanshift向量，通过迭代计算目标最优匹配位置。设定阈值σ，直到，迭代结束。

Step7：把y1代入自适应滤波器的修正方程中，把修正过后的值作为下一帧中目标位置预测的初始信息带入跟踪算法。依次重复第3步～第7步，直到视频帧处理完成。

3 实验结果与分析

3.1 实验环境及参数

本文在基于MATLAB R2017a的运行环境下对提出的跟踪算法进行实现，采用处理器为Intel（R）Core（TM）i5-8300 CPU @2.30GHz，内存为16GB的PC机进行编程实现。实验中，相邻两帧间隔时间t=1，AKF算法中的遗忘因子b=0.95，Meanshift算法迭代所设阈值σ=1。实验分为三个部分，分别对跟踪目标背景无干扰、跟踪目标背景有干扰和跟踪目标存在遮挡的情况，进行测试。

3.2 跟踪目标无背景干扰

为了进一步验证算法的可行性，对一段已知运动轨迹的跟踪视频序列进行处理，该视频文件共149帧，帧高度为1920px，帧宽度为1080px，视频格式为RGB24位，在实验中跟踪黄色小球的运动，在视频第102帧灰色小球碰撞黄色小球，使得黄色小球运动路径发生突变。通过对比本文算法和的KF-Meanshift算法，验证算法的可行性。图1为两种算法分别处理的序列第75帧、第110帧、第130帧的跟踪效果。再通过算法确定视频序列每一帧中跟踪目标的跟踪窗口中心轨迹，并将其绘制曲线和轨迹曲线加以对比。由图2和表1可以看出，本文的跟踪算法可以对目标实现跟踪，同时有着更好的效果。

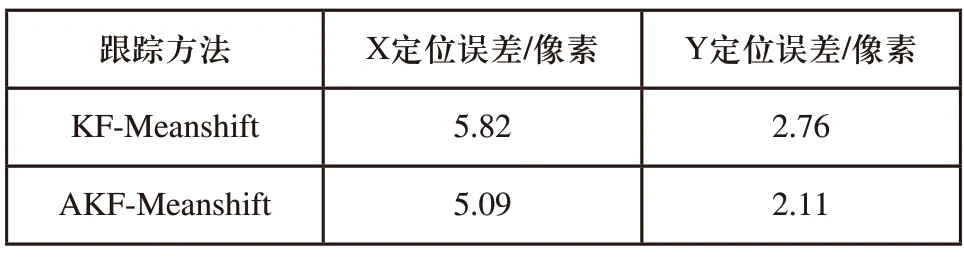
表1 视频跟踪误差

图1 视频无噪声跟踪目标跟踪效果

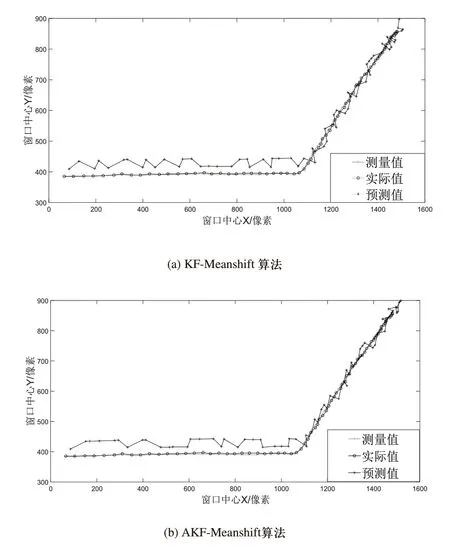
图2 视频无噪声跟踪目标窗口中心轨迹

3.3 跟踪目标存在背景干扰

对3.1中的视频序列增加随机噪声，在噪声未知的情况验证两种算法的效果。图3为两种算法分别处理的序列第81帧、第106帧、第125帧的跟踪效果。图3和图4可以看出，在视频序列有背景干扰，系统噪声未知的情况下，传统的KF-Meanshift算法在跟踪过程中丢失了目标信息，跟踪失败，而本文的算法实现了对目标的跟踪。

图3 视频有噪声跟踪目标跟踪效果

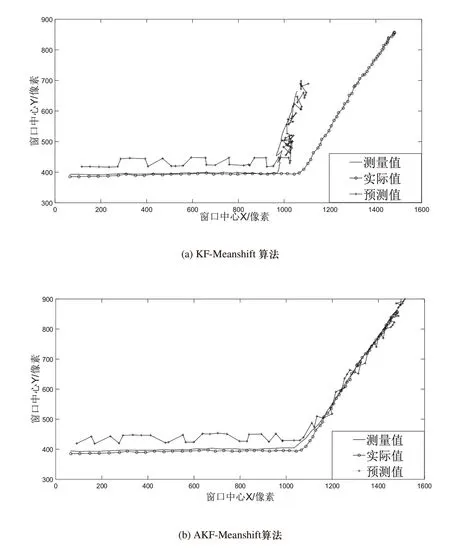
图4 视频有噪声跟踪目标窗口中心轨迹

3.4 跟踪目标存在遮挡

为了测试本文算法对于存在遮挡情况的运动目标跟踪的准确性，本文对Visual Tracker Benchmark视频库中Jogging视频序列进行目标遮挡的跟踪实验，在视频序列中身穿白色衣服的人为跟踪目标。图5为视频序列第37帧、第56帧、第65帧的跟踪效果，从图中可以看出当目标有遮挡情况，传统的Meanshift算法会丢失跟踪目标，造成跟踪失败，而本文提出的算法能够预测遮挡时的轨迹，在遮挡过后继续对目标跟踪，实现对目标整个运动轨迹的良好跟踪。

4 结语

本文采用了一种基于自适应卡尔曼的Meanshift算法实现对目标的运动的定位跟踪，有效解决了传统Meanshift算法在目标遇到遮挡时造成跟踪失败的问题。同时解决了卡尔曼Meanshift算法对系统先验信息的依赖性，改善了算法在复杂环境下的跟踪性能。实验测试表明，本文算法和传统算法相比，具有较大的优越性。