部分框支-剪力墙结构框支框架部分承担倾覆力矩的计算方法研究

曾庆立， 魏 琏， 王 森， 杜宏彪

(1 深圳大学土木与交通工程学院， 深圳 518060；2 深圳市力鹏工程结构技术有限公司， 深圳 518034)

0 前言

《建筑抗震设计规范》(GBJ 11-89)[1](简称89抗规)第6.1.13条规定 “……落地抗震墙数量不宜小于上部抗震墙数量的50%……”，对此，文献[2]的说明为框支层是结构的薄弱层，在地震作用下容易产生塑性变形集中导致框支层首先破坏甚至倒塌，因此应限制过多削弱框支层刚度和承载力。《建筑抗震设计规范》(GB 50011—2001)[3](简称01抗规)取消了落地墙数量不小于上部抗震墙数量的50%的规定。《建筑抗震设计规范》(GB 50011—2010)[4](简称10抗规)和《高层建筑混凝土结构技术规程》(JGJ 3—2010)[5](简称10高规)进一步对框支框架部分承担的地震倾覆力矩作出了规定。10抗规第6.1.9条规定 “……底层框架部分承担的地震倾覆力矩，不应大于结构总地震倾覆力矩的50%”；10高规第10.2.16条规定“框支框架部分承担的地震倾覆力矩应小于结构总地震倾覆力矩的50%”；文献[6]对此的说明是，若把框支层视为普通的框架剪力墙结构，当框支框架部分承担的地震倾覆力矩大于50%时，该框支层为少墙框架结构，对抗震不利。

现行软件主要是沿用10抗规关于框架-剪力墙结构的算法计算框支框架部分部分承担的倾覆力矩，如式(1)所示：

(1)

式中：n为结构层数；m为第i层框架柱的总根数；Vij为第i层第j根框架柱在规定水平力作用下的剪力；hi为第i层层高。

然而，现行软件在应用式(1)的抗规法时均存在一些问题和不足[7-8]，导致计算结果不能应用或存在疑惑，本文拟通过对现有软件框支框架部分承担倾覆力矩比算法的分析研究，指出其不足之处，并提出了抗规法及力偶法在部分框支-剪力墙结构的合理应用。

1 PKPM，ETABS软件算法

部分框支-剪力墙结构示意图如图1所示。pi为作用在图1(b)所示左侧隔离体的第i层水平外力；hi为第i层层高。当将式(1)应用于部分框支-剪力墙结构时，假设框支层在第k层，PKPM，ETABS等软件按照式(2)计算第s层(1≤s≤k)框支框架部分部分承担的倾覆力矩比ηfs：

(2)

式中:m为第i层框架柱的总根数；Vij为第i层第j根框架柱在规定的水平力作用下的剪力；Mov为结构底层倾覆力矩，可按式(3)，(4)计算，其中Vi为规定水平力作用下第i层的楼层总剪力，Fi为第i层的规定水平力。

(3)

Vi=Fi+Fi+1+…+Fn

(4)

式中n为结构层数。

将式(3)代入式(2)得

(5)

PKPM，ETABS等软件将式(5)应用于部分框支-剪力墙结构时，该式分子的部分仅包含了框支框架部分的剪力，由于框支层以上楼层不存在框支柱，其计算结果必然偏小。

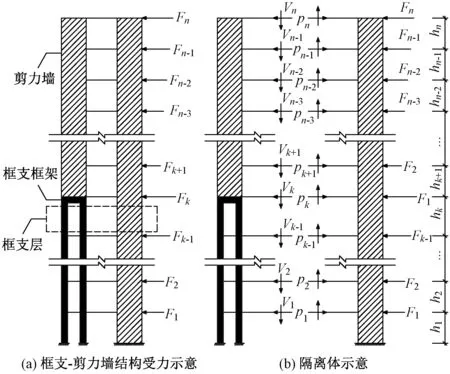
图1 部分框支-剪力墙结构示意图

在此假设第s层框支框架部分所占的楼层剪力比λfs为：

λfs=Vcs/Vs≤1

(6)

式中：Vcs为第s层框支框架部分分担的总剪力；Vs为第s层楼层总剪力；对于剪力墙均不落地的框支-剪力墙结构，λfs等于1；对于剪力墙落地的部分框支-剪力墙结构，λfs总小于1。

将式(5)应用于剪力墙均不落地的算例，对于第s层，由于λfs总等于1，其计算结果为：

(7)

即当采用式(5)计算剪力墙均不落地的框支-剪力墙结构，框支层及其下任意一层框支框架部分部分承担的倾覆力矩比总是小于1，由此可以判断式(5)的算法是不正确的。可进一步证明，对于部分框支-剪力墙结构，式(5)计算得到的倾覆力矩比是偏小的。

总存在一个折算系数λs使得式(8)成立。

λfsVshs+λf(s+1)Vs+1hs+1+…+λfkVkhk

=λsVshs+λsVs+1hs+1+…+λsVkhk

(8)

此时，式(5)可进一步表达为：

(9)

不妨假设第i层的规定水平力Fi可近似采用式(10)求得[4]:

(10)

式中：Gi，Gj分别为第i层、第j层的重力荷载代表值；Hi，Hj分别为第i层、第j层的计算高度;FE为总规定水平力。

又假定质量沿楼层均匀分布，层高均相同，则式(10)可简化为：

(11)

将式(11)代入式(4)得：

(12)

将式(12)代入式(9)并整理简化可得：

ηfs=λsβs

(13)

(14)

(15)

此处不妨称βs为倾覆力矩比计算系数。式(15)表明，倾覆力矩比计算系数βs与结构楼层总数及框支层所在的楼层位置有关，表1，2分别给出了不同楼层总数及框支层在不同位置时，底层以及框支层的倾覆力矩比计算系数的大小。

底层倾覆力矩比计算系数β1 表1

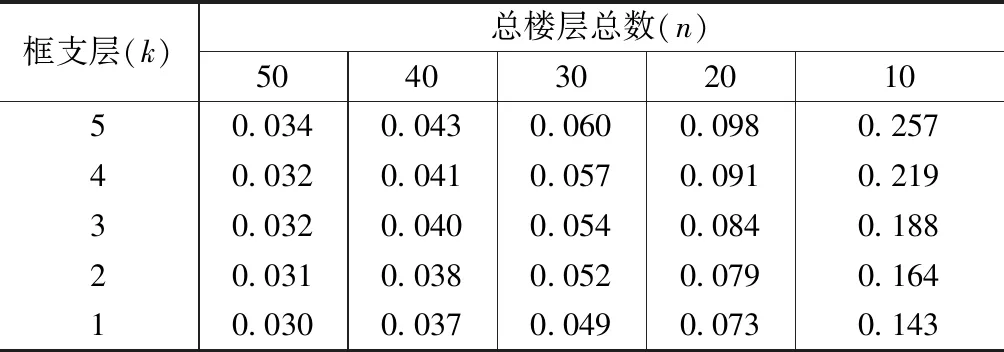
框支层倾覆力矩比计算系数βk 表2

表1，2结果表明，底层与框支层的倾覆力矩比计算系数随结构楼层总数的增加逐渐减小，随框支层所在位置的增加逐渐增大；进一步得到了不同楼层总数的部分框支-剪力墙结构，当框支层位置分别在底层、2层、3层、4层以及5层时，底层以及框支层的倾覆力矩比计算系数如图2、图3所示。由图2，3可知，当结构楼层总数相同时，框支层所在位置越靠近底部，其倾覆力矩比计算系数越小，由此计算得到的倾覆力矩比越小；同时，当框支层位置保持不变时，随着楼层总数的增加，倾覆力矩比计算系数越小。从图2，3可看出，当结构楼层总数不少于20层时，底层倾覆力矩比计算系数最大值小于0.4，框支层倾覆力矩比计算系数最大值小于0.1，其数值较小。

图2 底层倾覆力矩比计算系数

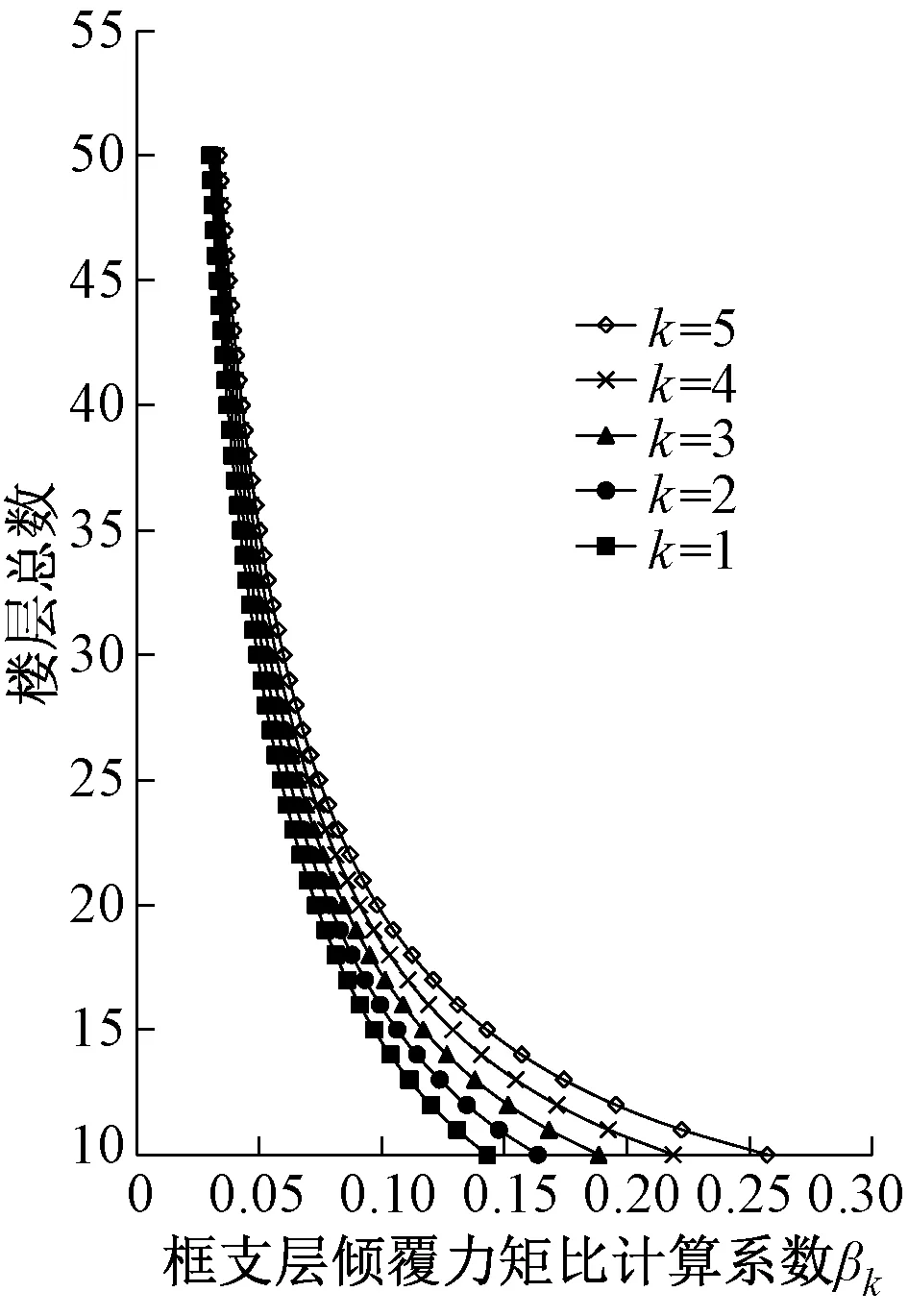
图3 框支层倾覆力矩比计算系数

综上分析，由式(13)计算得到的框支框架部分承担的倾覆力矩比偏小。在此以结构楼层总数为30层，框支层位置分别在底层、2层、3层、4层以及5层为例说明。由表1，2可知，当结构楼层总数为30层时，底层倾覆力矩比计算系数β1随框支层位置的变化其范围约为(0.049，0.244)，框支层倾覆力矩比计算系数βk随框支层位置的变化，其范围约为(0.049，0.060)；在此不妨假设λs无限接近于1，可以想象对应的情形是几乎所有剪力墙均未落地，根据表1，2的计算结果，此时底层框支框架部分承担的倾覆力矩比最大的只有约为0.244，框支层框支框架部分的倾覆力矩比最大的只有约为0.060；根据工程经验，对于大多数工程，λs基本达不到0.5，则本例中底层及框支层框支框架部分承担的倾覆力矩比分别0.122，0.03，恰恰说明了PKPM，ETABS等软件应用抗规法计算得到的倾覆力矩比偏小，这使得设计人员仅根据此计算结果及相关规范条文规定可能会作出落地墙数量已足够的不合理判断。

2 YJK软件算法

将式(1)应用于部分框支-剪力墙结构时，YJK软件提出了与上述软件不同的算法。

依然假设框支层在第k层，计算第s层的框支框架部分承担的倾覆力矩比ηfs时，YJK软件按式(16)计算。

(16)

式中Mov-p为规定水平力作用下框支层相邻上一层的总倾覆力矩。

根据式(3)，则式(16)的分母可表达为

(17)

将式(4)代入式(17)并整理得：

Mov-Mov-p=(Fs+F2+…+Fn)hs+(Fs+1+F2+…+Fn)hs+1+…+(Fk+Fk+1+…+Fn)hk

(18)

由此可见，YJK软件的算法实质是将图4(a)的计算模型转化成图4(b)的计算模型，即模型中将框支层上部楼层的规定水平力均作用于框支层，将框支层以下楼层视为框架-剪力墙结构，其框支框架部分部分承担的倾覆力矩计算方法与10抗规关于框架-剪力墙结构的算法相同。

[15] Robert Sutter, Chin-Hao Huang, “China-Southeast Asia Relations: Managing Rising Tensions in the South China Sea”, Comparative Connections, September 2011.

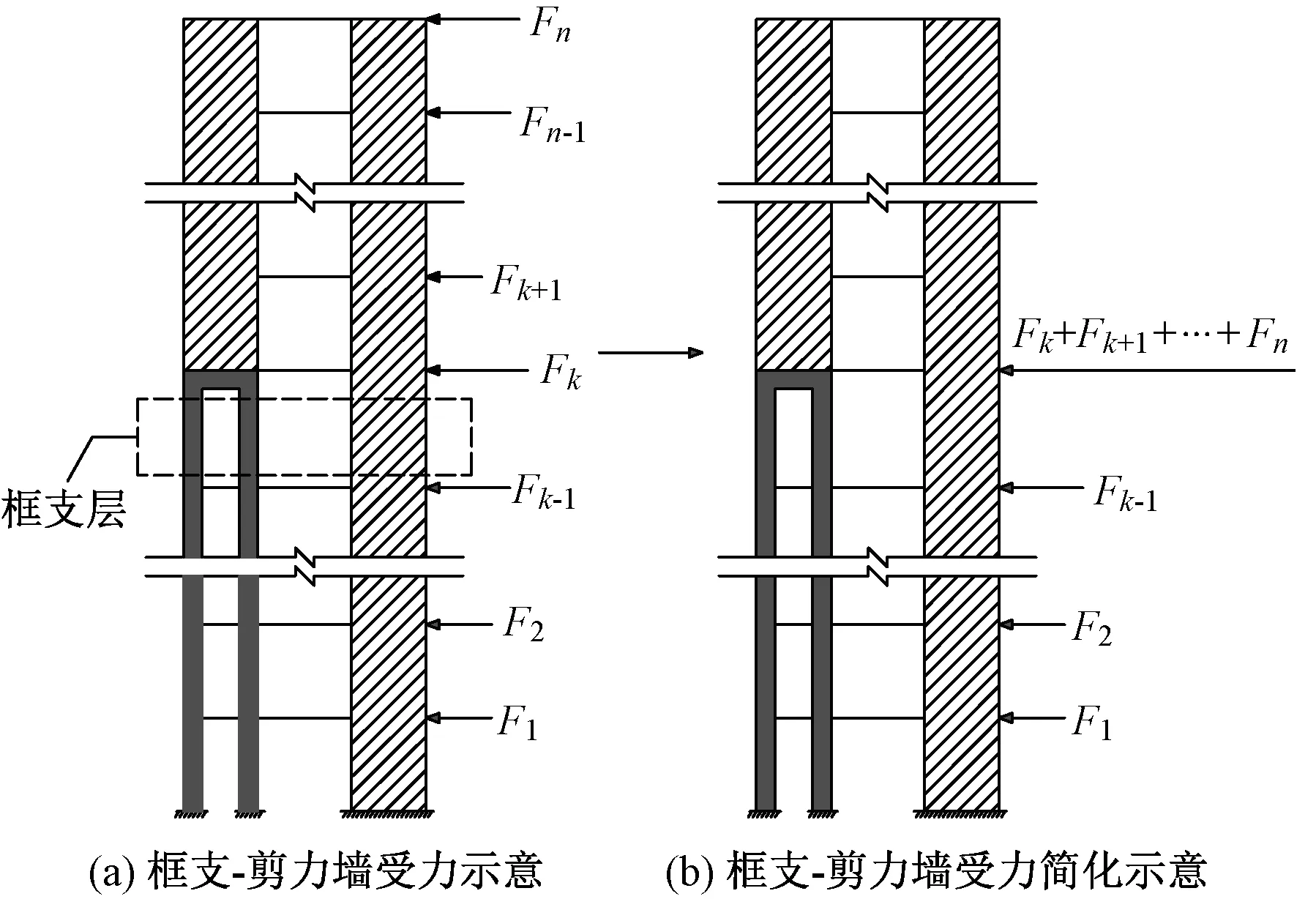
图4 YJK软件计算方法简图

由此可见，对比其他软件的算法，YJK软件的算法相当于将式(5)的分母部分扣除了框支层相邻上一层的倾覆力矩，使得YJK软件的算法计算结果较其他软件算法大，但该法仅仅考虑了框支框架部分的剪力，并未解决其他软件应用抗规法时存在的问题，其值实际上仍然偏小。

3 抗规法于部分框支-剪力墙结构的合理应用

根据文献[9]的研究，抗规法计算结果的实质是底层框架及以上隔离体所分配到的层水平外力对底层框架的力矩之和，由此可见，当抗规法应用于部分框支-剪力墙结构时，框支框架部分部分承担的倾覆力矩应为底层(框支层)框支框架部分及以上隔离体所分配到的层水平外力对底层(框支层)框支框架部分的力矩之和，如图1(b)所示左侧的带框支层隔离体，底层框支框架部分承担的倾覆力矩应为：

Mf=pn(hn+hn-1+…+h1)+

pn-1(hn-1+…+h1)+…+p1h1

(19)

对该式进一步简化后，得到本文建议的抗规算法：

(20)

对比现有软件，本文在应用抗规法时，不仅仅只包含框支层及以下各层框支柱的剪力，式(20)中还计算了框支柱及各非落地墙的剪力，其本质计算的是各层水平外力对底部框支框架部分的外力矩之和，该计算方法与抗规法在框架-剪力墙结构中的应用是一致的。

需特别指出，如图5所示的部分框支-剪力墙结构，承托非落地剪力墙的转换梁一侧支撑在框支柱另一侧支撑在落地剪力墙时，应用式(20)计算框支框架部分部分承担的倾覆力矩时，该公式是否能包括此转换梁所承托的非落地墙尚需要进一步深入的研究。

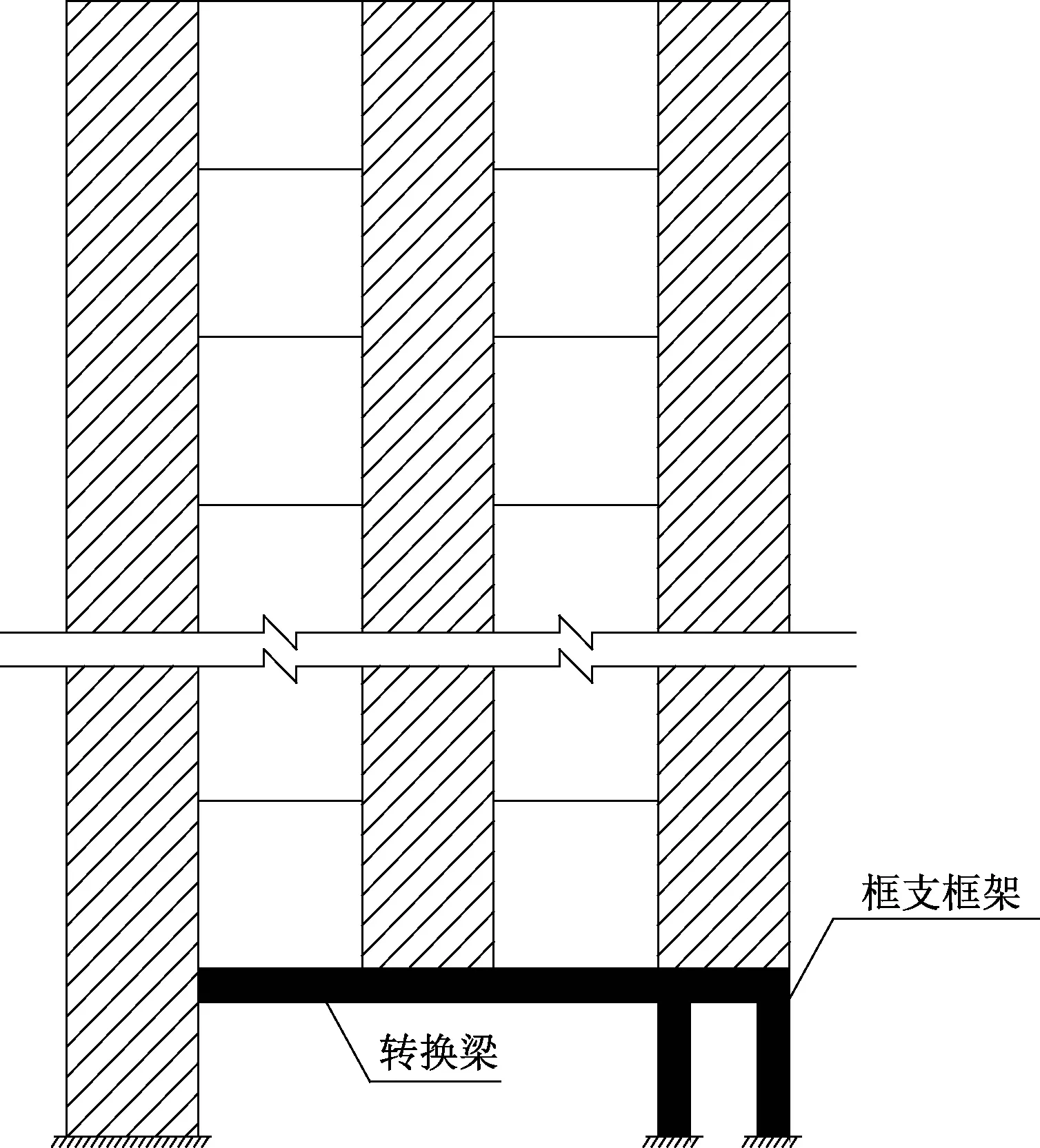
图5 转换结构示意图

4 轴力法

由于抗规法存在的种种问题，有学者[10]提出了基于结构底部竖向构件轴力及弯矩的轴力法，使用式(21)计算框架部分X向承担的倾覆力矩。

(21)

式中：n为底层框架柱的总数；Ni为结构底层第i根框架柱在规定水平力作用下的轴力；xi为第i根框架柱的横坐标;x0为取矩点的横坐标；Mci为第i根框架柱柱底弯矩。

因此，框支框架部分承担的倾覆力矩比例ηc为：

(22)

文献[7]指出轴力法存在不同求矩点计算结果不一致的问题。

5 力偶法于部分框支-剪力墙结构的应用

根据文献[9]的研究成果，对于框架-剪力墙结构而言，框架部分承担的倾覆力矩为：

(23)

(24)

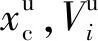
(25)

由此可得由力偶法计算得到的框支框架部分承担的倾覆力矩比为：

(26)

与式(2)的抗规法相比，力偶法考虑了竖向构件轴力及位置对抵抗外力矩的影响，更符合各竖向构件的实际受力状态；与轴力法相比，力偶法严格根据梁受力反弯点位置进行计算，理论严密合理。

6 算例

图6为非对称的部分框支-剪力墙结构算例，框支柱截面为1 000mm×1 000mm，转换梁截面b×h为500mm×1 000mm，连梁截面b×h为200mm×800mm剪力墙墙厚为200mm，混凝土强度等级均为C30。在图6所示水平力作用下，分别采用PKPM软件的抗规法、轴力法以及本文的抗规法、力偶法得到的框支层框支框架部分承担的倾覆力矩比，计算结果见表3。

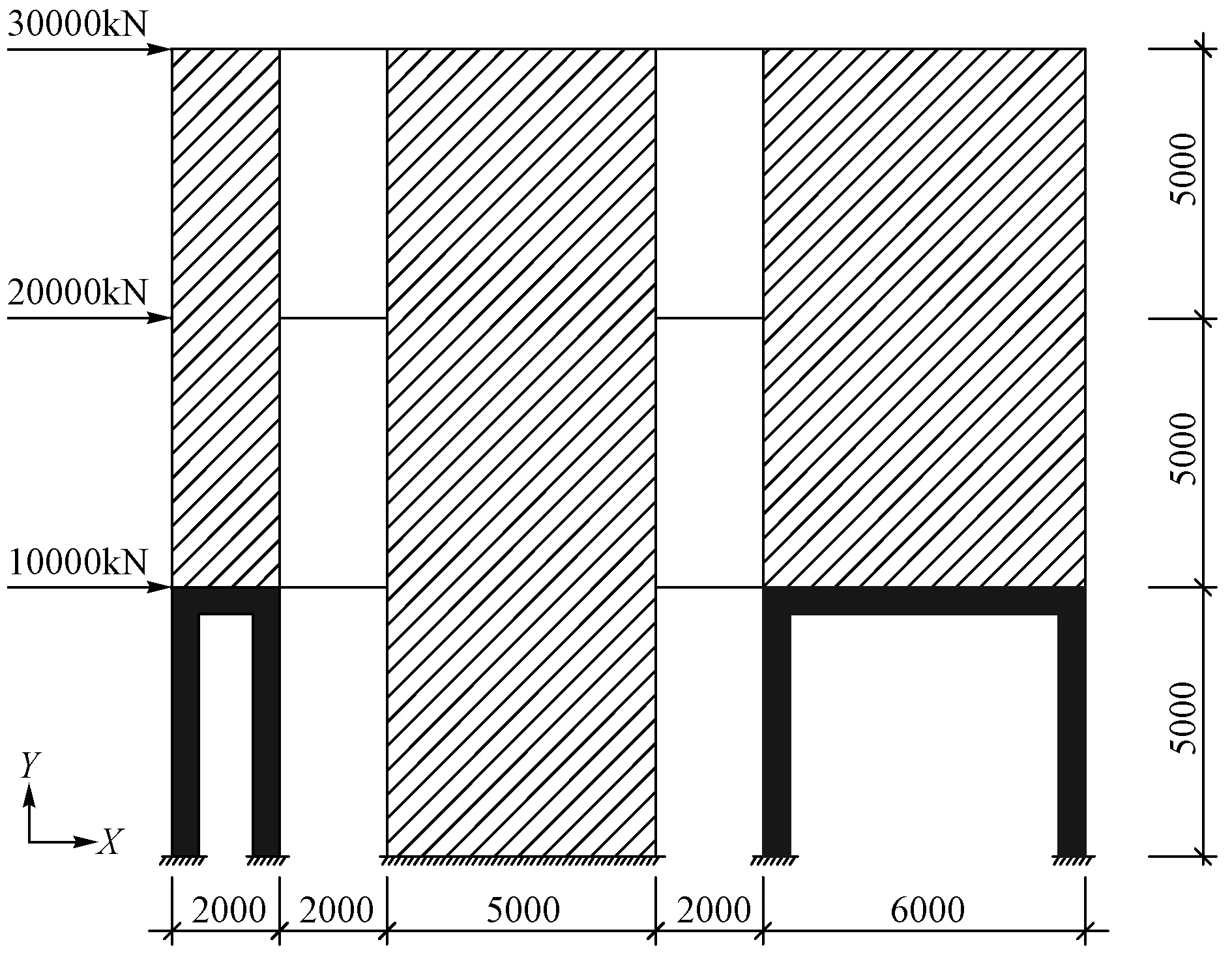
图6 部分框支-剪力墙结构案例示意图

X向框支框架部分承担的倾覆力矩比表3

表3计算结果表明，PKPM软件采用的抗规法计算结果为13.86%，此计算结果明显偏小，会造成不合理的判断；轴力法及力偶法的计算结果约为65.9%，而本文提出的抗规法计算结果为50.8%，比其他软件采用的抗规法大得多。由于不平衡轴力较小，由文献[9]可知，此案例的轴力法与力偶法计算结果接近。

7 结论

(1)PKPM，ETABS应用抗规法计算的框支框架部分承担的倾覆力矩占比偏小。

(2)YJK软件的算法将框支层以上的地震力集中在框支层后沿用抗规法计算倾覆力矩比，虽然计算结果较PKPM，ETABS软件的计算结果大，但仅仅

考虑了框支框架部分的剪力，其计算结果仍然是偏小的。

(3)轴力法考虑了框支柱底部轴力对抵抗外力矩的贡献是合理的，但计算结果会因求矩点的不同有所差异。

(4)抗规法应用于部分框支-剪力墙结构时，框支框架部分部分承担的倾覆力矩应为框支层框支框架部分及以上隔离体所分配到的层水平外力对框支层框支框架部分的力矩之和。

(5)轴力法求矩点定在底层的一个点，而力偶法则严格根据梁受力反弯点位置进行计算，理论严密合理，供工程界参考使用。