基于渐近式辐射传输模型的雪面反射率的计算验证

解文进，张伦雨，姜 苇，焦乘乘，田桂洪

(平塘县气象台，贵州平塘 558300)

积雪是地表覆盖的重要组成部分[1]，对气候环境变化十分敏感[2]。雪面反射率是全球地表辐射与能量平衡、全球变化研究中的一个重要参数，是衡量地表能量收支的重要指标[3]。积雪是地球表面最为活跃的自然要素之一，其特征(如积雪面积、积雪分布、雪深等)是全球能量平衡、气候、水文以及生态模型中的重要输入参数[4]。就全球和大陆尺度范畴而言，大范围积雪影响气候的变化、地表辐射平衡与能量交换、水资源的利用等；就局部和流域范畴而言，积雪影响天气、工农业和生活用水资源、环境、寒区工程等一系列与人类活动有关的要素[5]，且积雪在干旱区的水分平衡中发挥着极为重要的作用[6]。由于雪在可见光波段的高反射率作用，积雪已成为全球辐射平衡的重要决定因子[7]。雪面反射率受积雪的光谱特性、积雪的污染程度、粒子形状和所处环境影响，它不仅影响气候环境，还与人类生活息息相关[8]。因此，针对雪面反射率的研究显得极为重要。

在大气环流或气候模式中，通常用雪粒子的形状作为参数来确定雪面反射率及其变化[9]，但积雪粒子形状多样，MIE散射和DISORT模型不能快速、准确地计算不同形状积雪粒子的雪面反射率。引用渐近式辐射传送模型(Asymptotic Radiation Transfer Model，简称ARTM)和雪表面层雪粒径反演算法[10]，构建积雪参数反演模型来获取雪粒径与雪面反射率之间的关系，实现用ARTM模拟计算雪面反射率[11]。因此需要对雪面反射率光谱进行特征分析，并研究积雪环境、地形特征等对雪面反射率的影响。根据2013年12月12日至14日新疆玛纳斯河流域实测地面积雪数据资料，在分析高寒地区雪面反射率变化特征的基础上，重点利用ARTM对雪面反射率进行计算，再用实测值对计算值进行验证，分析ARTM计算雪面反射率的可靠性和有效性。

1 渐进式辐射传输模型与研究区数据采集

1.1 渐进式辐射传输模型

积雪粒子不完全是球形粒子，计算雪面反射率比计算球形粒子的反射率困难。Kokhanovsky和Zege建立了ARTM，ARTM基于以下假设：①像元完全被积雪覆盖；②积雪是由致密、随机朝向和不规则形状颗粒状粒子组成的弱吸收散射体；③忽略积雪水平和垂直的各向异性特征；④模型适用于波长小于1 400 nm的可见光-近红外波段；⑤假设冰的折射率不随波长变化，且等于1.31[12-13]。

将雪面的双向反射率因子(Bidirectional Reflection Factor)定义为雪面反射的辐亮度与朗伯表面反射的辐亮度之比，可写为

(1)

其中，θ0为太阳天顶角，θ为观测天顶角，φ为两者的相对方位角，Ir为雪面反射的辐亮度，IL为朗伯表面反射的辐亮度。IL=E0(θ0)cosθ0/π，E0为太阳入射辐照度。因此将上式用ARTM的双向反射率表达为

R(θ,θ0,φ)=exp[-αf(θ,θ0,φ)]。

(2)

其中，吸收参数α定义为[12]

(3)

σext和σabs分别为雪的消光系数和吸收系数；g(ξ)为不对称因子，ξ为形状参数，由颗粒的对称轴比值得到。雪的消光系数可表达为σext=3CV/2aef，aef为雪粒子半径。吸收系数表达为[12,14]σαbs=γφ(ξ)CV，其中，γ为冰的吸收系数，γ=4πχ/λ，受污染时γ=4π(χ+0.2CS)/λ，χ为冰的复折射率虚部，λ为入射波长，CS为污化物的体积比含量；φ(ξ)是吸收增强参数，由ξ决定；雪粒子体积浓度CV=Msnow/ρsnow，Msnow为雪的质量密度，ρsnow为雪的质量浓度。则α可表为

(4)

函数f(θ,θ0,φ)定义为[15]

(5)

其中，K0是逃逸函数，决定光子在半无限、无吸收介质中逃逸的角度分布，可近似写为[12,15]K0=3/7(1+2cosθ)。当cosθ≥0.2时，上式可用于计算雪的散射特性。R0(θ,θ0,φ)为弱吸收表面的双向反射率因子，可近似为[16]

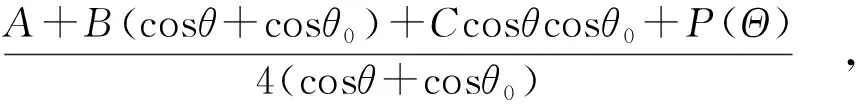
(6)

其中A=1.247,B=1.186,C=5.157；P(Θ)为散射相函数，近似为P(Θ)=11.1exp(-0.087x)+1.1exp(-0.014x)，x=arccos(-cosθcosθ0+sinθsinθ0cosφ)。

目前，ARTM可计算三种形状(分别为六边柱形、球形和二级科赫形)雪粒的雪面双向反射率，三种雪粒的不对称因子g(ξ)和吸收增强参数φ(ξ)由几何光学模型计算得到[17]，如表1所示。

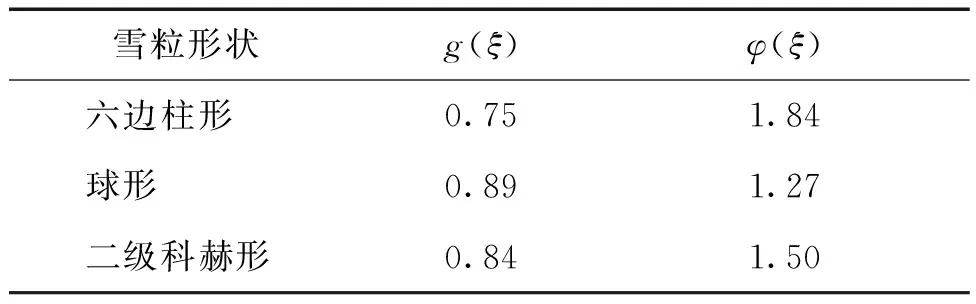
表1 三种形状雪粒的不对称因子g(ξ)和

1.2 数据采集

研究区位于新疆准噶尔盆地南缘的玛纳斯河流域，利用FieldSpec4高分辨率便携式野外光谱仪测定雪面反射率，其测量波长范围为350～2 500 nm，视场角为25°。辅助观测仪器包括观测雪层含水量使用的雪特性分析仪，观测雪粒径使用的40倍手持显微镜，以及GPS、红外温度枪、电子风速仪等[18]。为了在玛纳斯河流域中验证ARTM的可靠性和有效性，需在不同环境(分别选取下垫面为农田、裸土和草地)中对不同积雪表面状态进行观测，于2013年12月12日进入流域北部低山区，在下垫面为农田、裸土环境中进行为期2天的观测；然后于14日由玛纳斯河流域西南和东南两侧翻越山脊线进入流域，在下垫面为草地环境中观测。除了2013年12月14日晴朗无云外，其它观测日内均有不同程度的云量。为了获取高质量的光谱数据，选择云层散开、阳光照射的时段进行观测。光谱采集之前，对光谱仪进行15 min预热。同时为了避免阴影及光污染，测量人员穿着深色衣裤，面向太阳。测量时光谱仪探头垂直向下，距雪面1 m左右，使得对应地面采样面半径为27 cm。每次采集积雪样本光谱前后均进行参考板校准，记录参考板反射率。为避免随机噪声的影响，采用光谱仪配套的白板作为参考基准，每个样本面测量三次后取平均值作为最后的光谱结果。

2 雪面反射率光谱特性分析与ARTM精度验证

2.1 雪面反射率光谱特征

每一种地物由于其自身的物理条件、物质含量、形状等特点，具有自身特有的光谱反射率曲线，积雪也是一样。利用12月12日下垫面为裸土环境，积雪表面分别为结晶、粗糙和光滑的3个观测点的观测资料，分析雪面反射率光谱特性(见图1)。图1中3个观测点的雪面反射率光谱曲线的形状和趋势基本相同，雪面反射率都随着波长的增加总体呈下降趋势。在350～700 nm波段附近，光谱反射率较为稳定；从700 nm开始，反射率开始加速减小，到达1 020 nm附近，由于光被吸收形成了一个较小的吸收谷；随后在波长1 100 nm附近时，出现一个比较大的波峰；之后反射率开始呈直线性下降；之后又分别在1 300、1 820和2 250 nm附近分别出现波峰。当波长在1 800～2 500 nm之间时，由于水汽和噪声干扰过于强烈， 雪面反射率出现了比较密集的干扰波。

图1 实测雪面反射率特征曲线

在可见光谱波段，雪面反射率的最高点接近于1；在近红外区，雪面反射率下降比较快；在1 400 nm以后，雪面反射率下降到0.2以下，并且在1 450 nm和2 000 nm附近雪面反射率降至0.05以下，这是由于在这两处积雪对光谱有强烈的吸收作用。

2.2 ARTM精度验证

由雪面反射率光谱特性得知，雪面反射率随雪面状态发生变化，因此选取不同下垫面环境中不同雪面状态资料对模型进行检验。根据5条假设，分别利用不同观测点测得的不同雪粒形状的粒径大小代入模型，得到三种形状雪粒子的雪面反射率曲线，将其与实测反射率进行对比，得到反射率偏差曲线来验证模型的准确度。雪粒径大小为每个观测点观测的平均粒径。基于假设ARTM适用于计算小于1 400 nm的可见光-近红外波段的雪面反射率，因此主要分析小于1 400 nm波段实测值与计算值的吻合度，以及1 000 nm处波谷重合度，雪面反射率偏差绝对值≤0.25则表明模型适用。

2.2.1 下垫面为农田 农田是常见的下垫面类型，因此在下垫面为农田环境中选取了不同雪面状态的3个观测点(观测点1雪面结晶；观测点2雪面结晶且粗糙；观测点3雪面为0.5 cm新雪，少量草露出)对ARTM验证。将3个观测点的积雪粒子半径、太阳高度角和太阳方位角(见表2)等代入ARTM模型计算雪面反射率。将ARTM模型计算的雪面反射率与实况对比(图2)可见，在可见光波段，受雪面结晶(观测点1)、雪面结晶且粗糙(观测点2)影响，模型计算的雪面反射率发生了较大偏差，但偏差都不超过±0.25；观测点3由于表面为新雪，未受结晶影响，受少量草露出影响较小，模型计算的雪面反射率发生了较小偏差，在±0.1之内。在1 000～1 400 nm波段，3种不同雪面状态下，模型计算的雪面反射率也发生了较小偏差；在1 000 nm处，不同雪面状态下六边柱形雪粒子的计算结果与实况最为吻合。整体来看，不同雪面状态下模型计算的雪面反射率都满足偏差绝对值≤0.25精度要求，模型适用于下垫面为农田的环境。

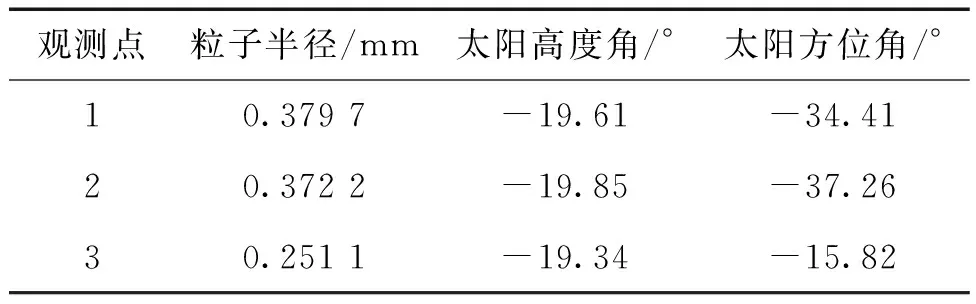
表2 下垫面为农田的3个观测点的粒子半径、

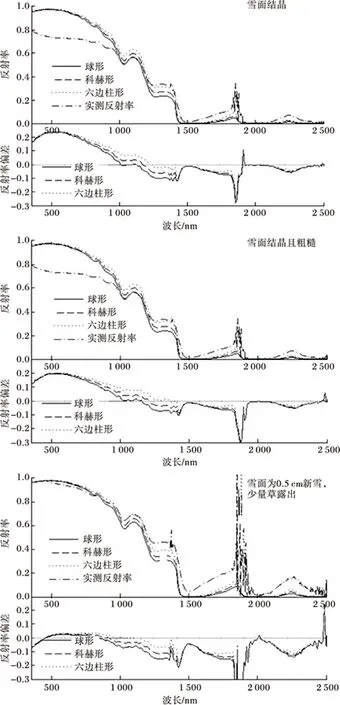
图2 下垫面为农田的不同雪面状态ARTM模型计算的雪面反射率和实测反射率及其偏差

2.2.2 下垫面为裸土 为了进一步验证ARTM在玛纳斯河流域中的有效性，再选取了下垫面为裸土的3个观测点(观测点4雪面结晶；观测点5雪面粗糙；观测点6雪面光滑)进行验证。将3个观测点的粒子半径、太阳高度角和太阳方位角(见表3)等代入ARTM模型计算雪面反射率。将ARTM模型计算的雪面反射率与实况对比(图3)可见，在可见光波段，受雪面结晶(观测点4)、雪面粗糙(观测点5)影响，雪面反射率发生了一定的偏差，但偏差在±0.2以内；观测点6雪面光滑，偏差很小。在1 000～1 400 nm波段，受雪粒形状影响，下垫面为裸土的不同雪面状态下模型计算反射率都发生了较小偏差，偏差都在±0.15以内；在1 000 nm处，不同雪面状态下六边柱形雪粒子计算结果与实况趋于重合。整体表明，不同雪面状态下模型计算的雪面反射率偏差都在±0.2以内，满足精度要求，模型适用于下垫面为裸土的环境。

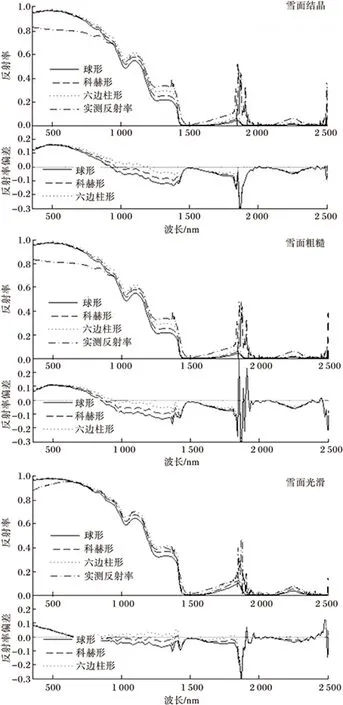
图3 下垫面为裸土的不同雪面状态ARTM模型计算的雪面反射率和实测反射率及其偏差

表3 下垫面为裸土的3个观测点的粒子半径、

2.2.3 下垫面为草地 玛纳斯河流域的中山区和山顶，积雪与枯草混合区、阴坡等积雪类型较为常见，故在此区域选取下垫面为草地的3个观测点(观测点7雪面无杂草露出；观测点8雪面为1.4 cm新雪，10°阴坡；观测点9雪面为1.4 cm新雪，山顶)进行验证。将3个观测点的粒子半径、太阳高度角和太阳方位角(见表4)等代入ARTM模型计算雪面反射率。将ARTM模型计算的雪面反射率与实况对比(图4)可见，在可见光波段，观测点8受坡度影响，雪面反射率发生了较小的偏差，偏差在0.11之内；而观测点7、观测点9在水平雪面观测，未受坡度影响，模型计算的雪面反射率与实测反射率曲线几乎重合。在1 000～1 400 nm波段，由于雪粒子形状的影响，下垫面为草地的3个观测点模型计算反射率偏差都小于0.11。在1 000 nm处，不同雪面状态下与实况吻合的雪粒形状有所差别，在观测点7和观测点8中，六边柱形雪粒子的计算结果与实况几乎重合，而观测点9，则是科赫形雪粒子的计算结果与实况最吻合。结果表明，不同雪面状态下模型计算的雪面反射率偏差都在0.11以内，满足精度要求，模型适用于下垫面为草地的环境。

表4 下垫面为草地的3个观测点的粒子半径、太阳高度角和太阳方位角

图4 下垫面为草地的不同雪面状态ARTM模型计算的雪面反射率和实测反射率及其偏差

3 结论

(1)雪面反射率随着波长的增加总体呈下降趋势。在可见光谱波段，雪面反射率最高点接近于1；在近红外区，雪面反射率下降比较快；在1 400 nm以后，反射率整体较低，在1 800～2 500 nm，由于水汽和噪声干扰过于强烈，雪面反射率出现了比较密集的干扰波。

(2)下垫面为农田环境中，可见光波段，受雪面结晶和雪面粗糙影响导致ARTM模型计算的雪面反射率与实况偏差较大，但满足偏差绝对值≤0.25精度要求。下垫面为裸土环境中，在可见光波段内同样雪面结晶和雪面粗糙导致雪面反射率发生了一定偏差，但雪面反射率偏差在±0.2以内。下垫面为草地环境中，模型在无坡度的情况下误差最小，随坡度出现会发生较小的误差，但最大偏差不超过0.11。ARTM模型计算雪面反射率可靠且有效。