油在分形有机纳米毛细管中的有效渗透率

王桂芹，周蔚怡，杨 勇

（1.延安大学石油工程与环境工程学院，陕西延安 716000；2.延长油田富县采油厂，陕西延安 716000）

近年来，随着页岩油气勘探开发的成功，人们已经认识到页岩不仅具有“源、盖层”的功能，而且还具有储层的功能。页岩储层已引起普遍关注，成为研究热点[1，2]，储存在页岩中的石油，称为页岩油，它是非常规石油的重要组成部分[3]。据估计，全世界页岩油的可采储量为6.89×1011t，约为常规原油储量（碳酸盐和砂岩）的三倍[2]。特别是，美国的几个大型非常规地层（Bakken，Eagle Ford，Niobrara 等）的产量已接近美国国内产量的一半。我国鄂尔多斯盆地、松辽盆地以及准格尔盆地等也已发现了丰富的页岩油资源[4]，然而，页岩被称为“致密”岩石，是一种典型的纳米孔介质，广泛存在有机纳米级孔隙[5]，为了模拟油在页岩油藏多孔介质中的流动，首先需要建立单个有机纳米孔中油的流动模型。

Pit 等[6]采用光漂白后的全内反射-荧光恢复实验方法，得出了第一个直接的实验结果，即十六烷在疏水性光滑表面上流动时存在明显的滑动。Majumder 等[7]通过由7 nm 对齐的碳纳米管组成的膜，实验测量了几种液体（己烷、癸烷、乙醇）的滑移长度。他们发现这些碳氢化合物的通量比无滑移泊肃叶定律预测的要大4～5 个数量级。Whitby 等[8]也有类似的实验结果。滑移是一个古老的概念，由Navier 提出，且有很多实际的用途[9，10]。Wang 等[11，12]利用MDS（分子动力学模拟）研究了辛烷通过石墨烯纳米孔的流动，计算出石墨烯纳米孔流动增强因子为1～3 个数量级，因为滑移长度太大，速度分布可能从抛物线形状变为塞子形状。Mattia 和Calabro[13]推导了碳纳米管中油的滑移速度表达式。在此基础上，考虑通过表面扩散和附着功的固液相互作用的影响，以及管的几何特性得到了描述流动增强的理论公式。Cui 等[14]推导了一个包含边界滑移和物理吸附的流动增强模型。在此基础上进行了敏感性分析，研究了物理吸附和边界滑移对流动的贡献。利用归一化速度的概念，定量地研究了有机纳米孔中速度剖面的形状与孔隙长度和孔径的函数关系。Secchi 等[10]通过实验发现在碳纳米管中的流动滑移是强烈依赖于孔隙半径而变化的。Zhang 等[2]通过考虑边界滑移和约束油的黏度变化以及依赖孔隙半径变化的滑移长度建立了一个原油通过单个纳米孔的输运模型。

上述学者都是基于平直纳米孔隙建立的单个有机纳米孔中油的流动模型，而实际页岩储层纳米孔隙都是弯曲的[15]。页岩储层多孔介质中的弯曲纳米孔隙满足分形理论[16，17]，很多学者已经采用分形几何理论来研究页岩多孔介质中气体流动[18-20]，但采用分形理论分析油在页岩储层中的流动还是很少[21]，员美娟等基于分形理论研究了各种非牛顿流体在分形毛细管中的流动特征[22-24]，本文基于Zhang 等建立的考虑边界滑移和物理吸附的有机纳米孔油的流量方程，结合实际弯曲毛细管的分形特性，建立油在单个分形毛细管中流动的流量、平均流速以及有效渗透率分形模型，分析孔隙半径、压力梯度以及弯曲分形维数对各模型的影响。为进一步研究页岩油藏多孔介质中油的流动，打下理论基础。

1 油在有机纳米毛细管中流动的分形模型

1.1 流量

综合考虑油在有机纳米管中流动时存在的边界滑移和吸附油的黏度变化，油在单根有机纳米毛细管中的流量方程为[2]：

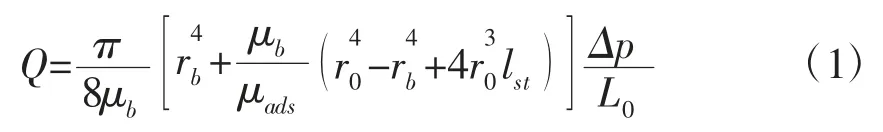
式中：Q-油在单根有机纳米毛细管中流动的体积流量；r0-有机纳米毛细管的半径；rb-体相油的流动半径；Δp-施加在有机纳米毛细管两端的压降；L0-有机纳米毛细管通道的直线长度；μb、μads、lst-描述油在有机纳米毛细管流动特性的常数，其中μb、μads分别为油的体相黏度和吸附黏度，lst为滑移长度。

（r0-rb）为吸附层厚度，在油-固相相互作用下，近壁面4 层油的密度和黏度将受到影响[25，26]。但是，第3层和第4 层的密度和黏度与体相值相差不大，对油流的影响可以忽略不计。因此，近壁含油区域的厚度可以直接假设为0.96 nm[12]，即辛烷分子直径（单层0.48 nm）的两层厚度。所以，有机纳米毛细管中体相油的流动半径为：

Wang 等[11]利用石墨烯代表有机孔，辛烷代表页岩油，利用MD 模拟，得到了滑移长度与孔径、外力、温度之间的经验指数关系：

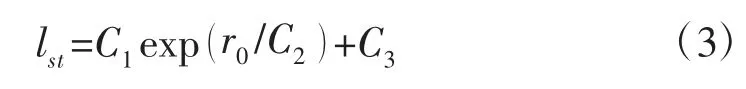
式中：C1、C2、C3-拟合常数。

Zhang 等[2]利用小剪切速率下的恒定滑移长度值和指数方程，获得可应用于油在页岩多孔介质有机纳米孔中流动实际情况下的滑移长度方程：

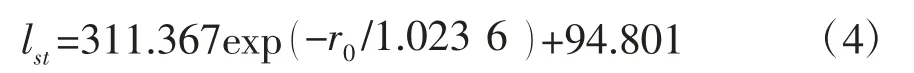
式（1）是基于平直纳米管获得的油的体积流量方程，而实际页岩多孔介质中纳米孔隙是弯曲的。流体流动的弯曲有机纳米毛细管的长度与半径服从如下分形关系[27，28]：

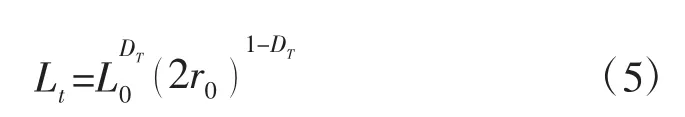
式中：Lt-页岩中有机纳米毛细管通道的实际长度，且Lt≥L0；DT-页岩中有机纳米毛细管的迂曲度分形维数，1≤DT≤3。

考虑到油在有机纳米毛细管中流动时流线的分形特征，采用毛细管的实际长度，结合（1）、（2）、（4）和（5）可得油在实际弯曲有机纳米毛细管中流动的分形流量方程：

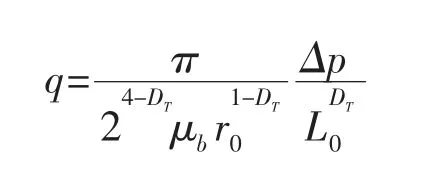
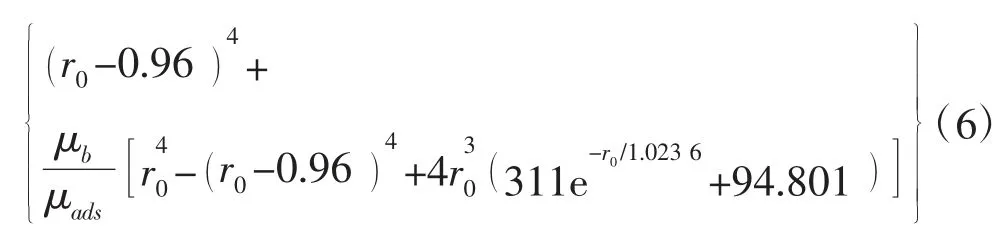
忽略油在有机纳米毛细管中流动时的吸附和速度滑移流动机理，即式（1）中rb=r0，lst=0 可得油在有机纳米毛细管中流动不考虑吸附和速度滑移的流量分形表达式：

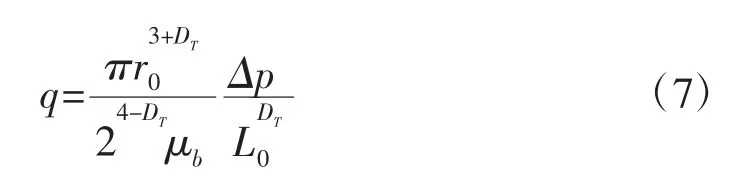
式中：当DT=1 时，可得油在无滑移直管中流动时的泊肃叶方程：

式（6）给出了油在有机纳米毛细管中流动时考虑边界滑移、边界层黏度变化以及滑移长度随半径变化的流量方程的分形表达式，从式（6）可以看出毛细管半径、边界层流体特征参数、迂曲度分形维数以及压力梯度都是影响有机纳米毛细管中流量的因素。

为了有效分析油在有机纳米毛细管中流动增强行为，引入无因次参数流动增强因子ε：

1.2 平均流速

由有机纳米毛细管中油流动的分形流量模型式（6）可得有机纳米毛细管中考虑油在其中流动时的各种流动机理的平均流速：

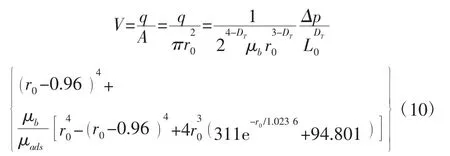
式中：A-单根有机纳米孔隙的横截面积。

从式（10）可以看出，与考虑油在有机纳米毛细管中流动时的各种流动机理的体积流量分形模型一样，油在有机纳米毛细管中流动的平均流速分形模型受有机纳米毛细管的迂曲度分形维数DT、有机纳米毛细管半径r0、施加在有机纳米毛细管两端的压力梯度（Δp/L0）以及油在有机纳米毛细管中流动的特性参数（μb、μads）的影响。

式（10）中，若不考虑油在有机纳米毛细管中流动时的速度滑移，吸附层等流动微观机理，可得油在有机纳米毛细管中流动时只考虑毛细管分形特征的平均流速表达式：

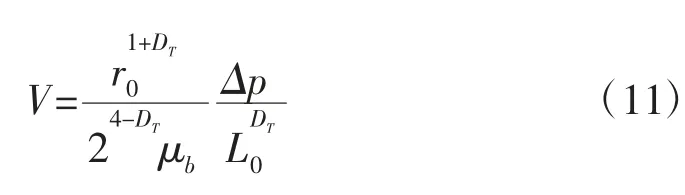
当DT=1 时，可得油在单根平直有机纳米毛细管中流动时的平均流速：

1.3 有效渗透率

单根有机纳米毛细管中的流体流动仍然遵循广义达西定律[29]：

式中：ke-有效渗透率。

结合式（6）和（13），可得油在单根有机纳米毛细管流动的表观渗透率：

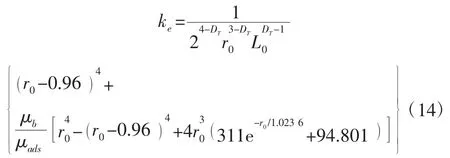
式（14）中，若不考虑有机纳米管中油流动时的速度滑移、边界层等流动机理，即可得只考虑有机纳米毛细管分形特征时油的有效渗透率：

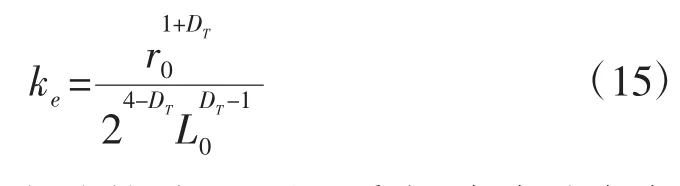
根据式（14）和（15）的对比，可以看出，考虑油在有机纳米毛细管中流动时的各种流动机理，油的流动特性参数以及毛细管的结构参数均是影响油在有机纳米毛细管中流动时有效渗透率的参数。而不考虑油在有机纳米毛细管中流动时的多重流动机理，油的流动特性参数不再影响油的有效渗透率，只有毛细管的结构参数影响油的有效渗透率。

毛细管的本质渗透率为：

为了进一步说明油在分形有机纳米孔中独特的输运行为，引入渗透率修正系数λ：

2 结果与讨论

不考虑油的黏度随压力和温度变化，有机纳米孔中边界层油的黏度是体相油的1.1 倍[2，14]。根据参考文献[30]令μb=1.5 mPa·s，同时令有机纳米毛细管长度L0=50 μm。

令有机纳米毛细管半径r0=50 nm，油在有机纳米毛细管中流动时的体积流量随有机纳米毛细管迂曲度分形维数以及施加在毛细管两端压力梯度的变化规律（见图1）。根据图1 可以得出，施加在毛细管两端的压力梯度越大，油的体积流量就越大，且油在有机纳米毛细管中流动时不存在启动压力梯度；而在相同压力梯度条件下，有机纳米毛细管迂曲度分形维数越大，油在其中流动时的体积流量就越小，即毛细管越弯曲，油在毛细管中流动时受到的阻力越大，流速就会变小，从而导致在毛细管中流动的流体流量变小。令Δp=2 MPa，油在有机纳米毛细管中流动时的体积流量以及流动增强因子随毛细管半径和迂曲度分形维数的变化规律（见图2，图3）。从图2 可以看出有机纳米毛细管中油的体积流量会随毛细管半径的增大而不断增大，与实际情况相符；但会随着毛细管迂曲度分形维数的增大而不断减小，即在相同半径和压力梯度条件下，毛细管弯曲程度会影响毛细管中的流量，毛细管越弯曲，流量越小，与上述结论相同。从图3 可以看出弯曲有机纳米毛细管中流动增强因子为1～3 个数量级。同时，从图中还可以看出流动增强因子会随着毛细管半径的增大而变小，这是因为有机纳米毛细管中油的滑移长度会随着孔隙半径的增大而减小；此外，还可以从图3 中看出毛细管迂曲度分形维数越大，流动增强因子越小，这是毛细管迂曲度分形维数变大导致流量变小所致。

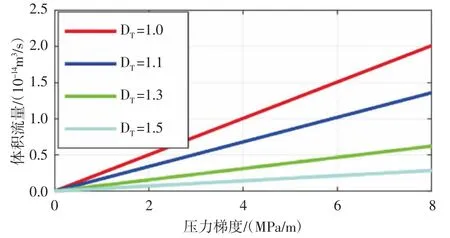
图1 体积流量随压力梯度与迂曲度分形维数的变化趋势

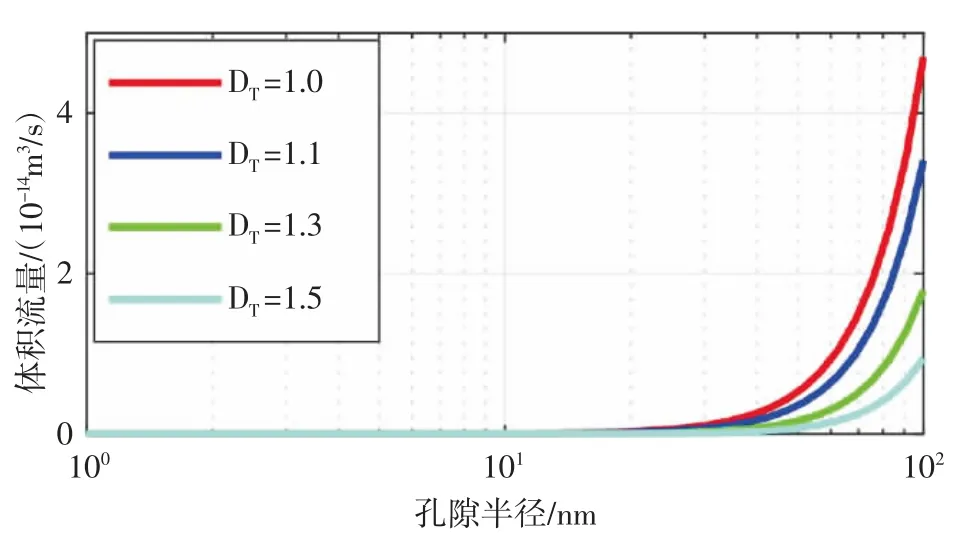
图2 体积流量随孔隙半径与迂曲度分形维数的变化趋势

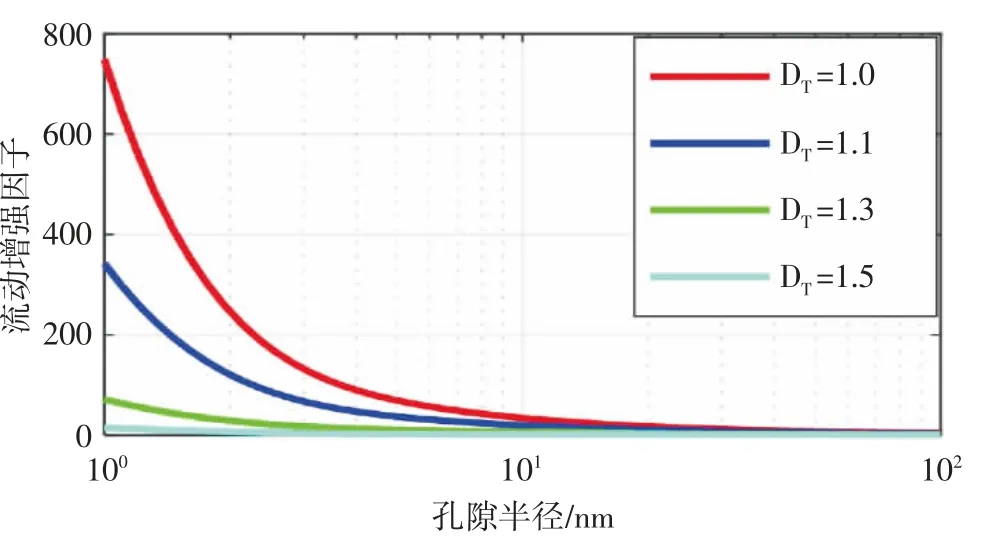
图3 流量增强因子随孔隙半径与迂曲度分形维数的变化趋势

同样令有机纳米毛细管半径r0=50 nm，油在有机纳米毛细管中流动时的平均流速随有机纳米毛细管迂曲度分形维数以及施加在毛细管两端的压力梯度的变化规律（见图4）。从图中可以看出，施加在有机纳米毛细管两端的压力梯度越大，有机纳米毛细管中油的平均流速就越大；而在相同压力梯度条件下，有机纳米毛细管迂曲度分形维数越大，油在其中流动时的平均流速就越小，即有机纳米毛细管迂曲度分形维数越大，油在其中流动时受到的流动阻力就越大，油的平均流速就会变小，与流量的结论相符。为了保持统一仍然令Δp=2 MPa，有机纳米毛细管中油的平均流速随孔隙半径与迂曲度分形维数的变化趋势（见图5）。从图中可以看出油的平均流速会随着孔隙半径增大而增大，而会随着迂曲度分形维数的增加而变小，与流量变化规律一致。

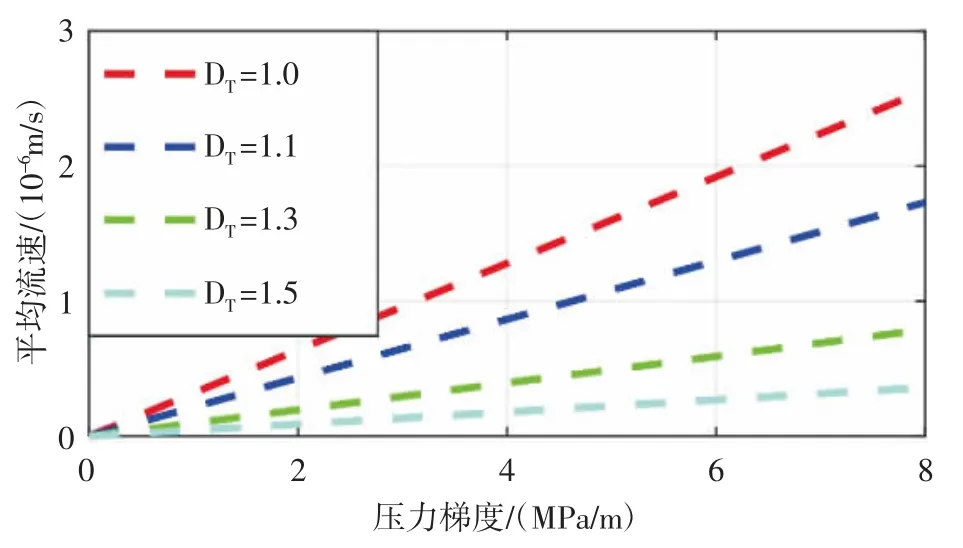
图4 油的平均流速随压力梯度和迂曲度分形维数的变化趋势

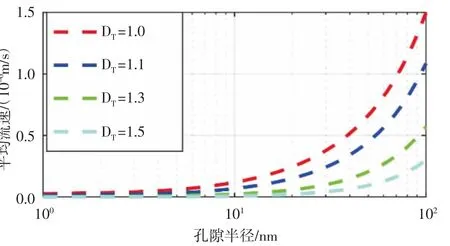
图5 油的平均流速随孔隙半径和迂曲度分形维数的变化趋势

从式（14）可以看出，有机纳米毛细管中油的有效渗透率与压力梯度无关，油在有机纳米毛细管中流动时的有效渗透率和渗透率修正系数随有机纳米毛细管半径和毛细管迂曲度分形维数的变化趋势（见图6和图7）。根据图6 可以得出，有机纳米毛细管半径越大，油在其中流动时的有效渗透率就越大，与实际相符；而有机纳米毛细管的迂曲度分形维数越大，油的有效渗透率就越小，且有机纳米毛细管半径大于10 nm时，分形有机纳米毛细管中油流动的有效渗透率受迂曲度分形维数影响就越大。从图7 可以得出，渗透率修正系数会随有机纳米毛细管半径增大而不断变小，这是因为有机纳米毛细管中油的滑移长度会随着孔隙半径的增大而减小；而有机纳米毛细管的迂曲度分形维数越大，油的渗透率修正系数就越小，这是因为毛细管迂曲度分形维数越大，毛细管就越弯曲，油在有机纳米毛细管中流动受到的阻力越大。

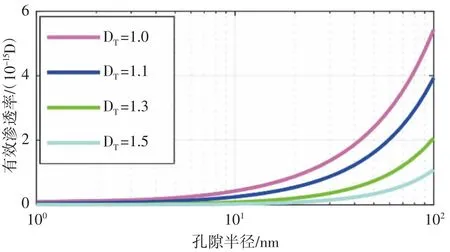
图6 油的有效渗透率随孔隙半径和迂曲度分形维数的变化趋势

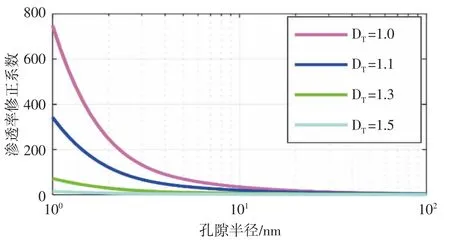
图7 油的渗透率修正系数随孔隙半径和迂曲度分形维数的变化趋势

3 结论

（1）有机纳米毛细管中油的体积流量会随着压力梯度和孔隙半径的增大而不断增大，但会随着有机纳米毛细管迂曲度分形维数的增大而不断减小。有机纳米毛细管中油的流动增强因子为1～3 个数量级，流动增强因子会随着毛细管半径和迂曲度分形维数的增大而变小，且半径越小，迂曲度分形维数对流动增强因子影响越大。

（2）油在有机纳米毛细管中流动时的平均流速会随着施加在有机纳米毛细管两端的压力梯度以及有机纳米毛细管半径的增大而增大，但会随着有机纳米毛细管迂曲度分形维数的增大而减小，与流量的变化趋势相同。

（3）油在有机纳米毛细管中流动时的有效渗透率会随着有机纳米毛细管半径的增大而增大；而有机纳米毛细管迂曲度分形维数越大，油在其中流动时的有效渗透率就越小，且有机纳米毛细管半径大于10 nm时，油在其中流动时的有效渗透率受迂曲度分形维数的影响就越大。油在有机纳米毛细管中流动时的渗透率修正系数会随有机纳米毛细管半径以及有机纳米毛细管迂曲度分形维数的增大而不断变小。