齿轮传动系统传动轴模态仿真及振动实验测试研究

王冰

(烟台汽车工程职业学院，山东 烟台 265500)

0 引言

当前，齿轮传动结构被广泛应用于车辆动力系统、减速机等领域，已经成为工业制造过程的一项必不可少的组成部分[1-3]。由于齿轮在实际运行过程中受到各类外部因素的综合影响，使其运行状态发生变化，无法获得精确的加工尺寸，严重时还会引起齿轮传动故障的问题。由于采用现有技术还无法对故障信号进行准确分析，在系统运行过程中，传动轴振动状态会降低系统的稳定性[4-5]。为了便于对上述不确定性因素进行分析，许多学者在构建模型的过程中都进行了适当简化处理，再利用动力学计算的方法得到最终结果。采用上述处理方法对齿轮结构和系统性能进行分析，最后对设计方案进行优化并分析了系统的运行可靠性[6-7]。

根据前期文献关于齿轮结构传动轴的动力学研究内容可知，已有许多学者开发了多种计算方法，主要包括时域法、代数分析法等。采用微分处理方法对系统运动过程进行了行动力学分析，同时建立了相应的传递函数[8-9]。同时也可以选择不同的方法来完成求解计算。其中，时域方法可以对系统中各零部件在不同时域条件下的时变动态参数进行分析，以频域法进行处理时则可以得到各项系统参数在每种频域条件下的具体状况。此外，齿轮运行状态还会受到时变啮合刚度以及实际尺寸精度参数的综合影响，因此在各个时间段中发生了周期性激励变化的现象，采用时域处理方法也表现出了同样的周期性响应特征[10]。以上研究结果表明，可以通过分析研究对象发生的时域和频域变化状态，实现对系统响应频率的精确分析，同时建立得到更加准确的激励、响应关系。

1 模态叠加模型建立

对多自由度系统进行分析的过程中，还应将黏性阻尼的因素也考虑在内，采用以下微分方程表示系统受迫振动的运动形式：

(1)

式中：M、C、K为对角矩阵；F为受迫振动力。将对角线元素表示成如下矢量形式：

(2)

式(2)是在n自由度下对应的运动方程，根据振动理论进行计算。

(3)

其中：hi(τ)是单位脉冲响应函数。其表达式为

(4)

式(4)是多自由度系统受到激振力作用的情况下出现的响应结果，并且各阶模态都会对激振力造成不同程度的作用。

2 传动轴模态分析

2.1 传动轴模态建立

本文研究的齿轮传动结构由四级减速系统构成，具体传动结构见图1。行星轮处于低速传动的状态下时，通过传动轴进行输出，需要同时承受输入轴与负载形成的转矩作用。当传动轴结构发生变形时，传统系统的内部结构难以精确啮合，导致齿轮箱运行过程出现故障。根据以上研究结果，为了对系统振动状态开展更加深入的分析，避免发生共振的问题，对传动轴模态差异性和振型特点进行了研究，同时确认是否因为共振的问题而引起行星齿轮运行过程出现异常。图2为模态分析的具体过程。

图1 齿轮传动系统结构组成示意图

图2 模态分析流程

采用QT500传动轴作为测试对象，传动轴输出通过轴承进行支撑，依次设置了Cylindrical Support和Displacement两种约束方式。

2.2 传动轴模态结果分析

以Modal 模块对传动轴结构进行仿真测试。对图3进行分析可以发现，在6阶模态下分析时，传动轴出现了局部扭转和振动的结果，提高模态阶数的过程中，振型变得更明显。其中，前2阶模态只沿某一特定的方向发生了变形，但3-6阶模态发生了扭转。

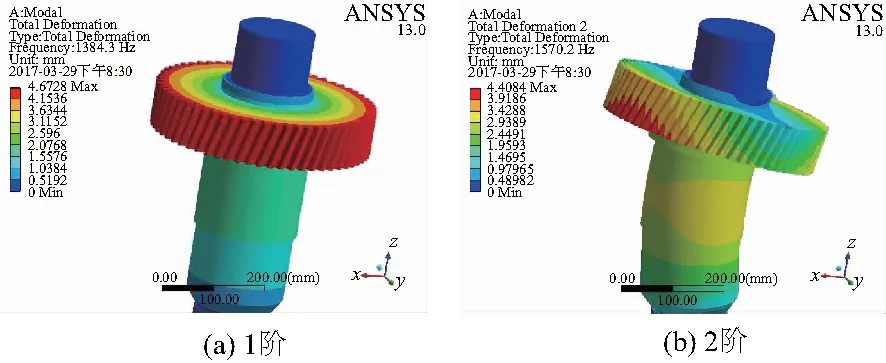
图3 传动轴模态变形云图

为实现齿轮传动系统的安全稳定运行过程，需选择抗振性优异的传动轴。本文研究的传动轴由四级减速结构组成，同时建立模态叠加模型，对传动轴模态特征进行了分析，之后测试了轴承振动和加速度参数。表1对应前6阶模态传动轴的固有频率分布结果。对前6阶模态频率以及振型参数进行分析可知，传动轴发生了局部振动并存在扭转的现象，当模态阶数增大后，获得了更明显振型。传动轴前6阶频率介于625～1339Hz之间，并且最低固有频率也大于最高啮合频率，从而避免了齿轮箱与传动轴发生共振的问题。采用MED分解加速度振动信号，得到前2阶IMF分量，再通过切片双谱测试减小模态混叠程度，达到信号数据简化的效果，以上测试结果表明，可以通过实验分析过程设计传动轴结构。

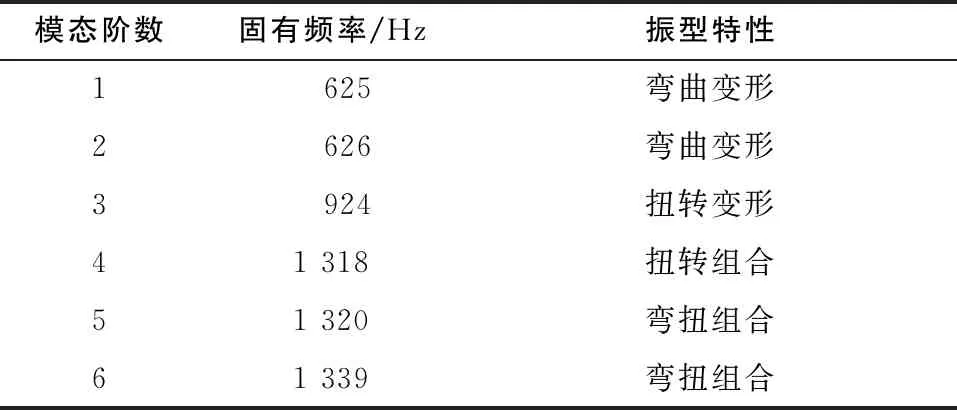
表1 对应前6阶模态传动轴的固有频率分布

对表1测试结果进行分析可知，随着模态阶数的增加，频率也发生了增大。传动轴的前6阶固有频率介于610～1324Hz之间，齿轮系统转频介于1.3～581.3Hz之间，经对比发现，传动轴最低固有频率已经超过最高啮合频率，因此可以避免齿轮箱与传动轴出现共振的情况。

3 传动轴振动试验

选择四级减速结构作为测试平台，图4为测试平台组成结构。齿轮传动比等于1∶1，保持1 200 r/min的转速，以12 000 Hz的频率进行采样，按照逐级方式完成载荷的加载过程，逐渐提高负载到800 Nm，使用CA-YD-186压电传感器。利用MED对传动轴振动信号进行处理。仿真数据如图5所示。

1—调速电机；2—联轴器；3—传动齿轮箱；4—转速仪；5—扭力杆；6/7/8/9—压电式加速传感器；10—试验齿轮箱。图4 齿轮传动试验台

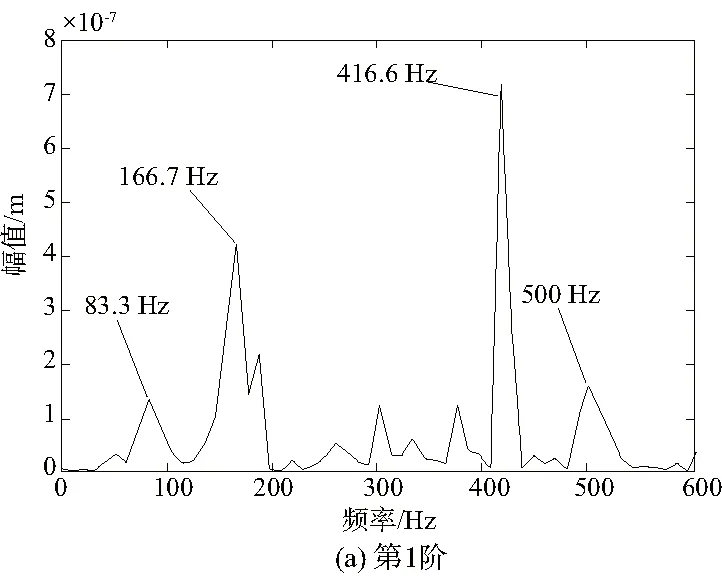
图5 齿轮振动信号前2阶IMF分量经MED分解后进行切片双谱分析

从图5中可以看到,通过MED对仿真数据进行处理获得的最初2阶IMF分量，之后进行切片双谱分析，从图5(a)中可以发现，低频部分形成了故障频率等于360Hz的一倍、二倍频，同时获得了更明显的三倍、四倍频，根据以上分析可以判断采用上述方法能够大幅降低高斯噪声导致的低频弱故障概率。图5(b)显示形成了更显著的三倍频1080Hz和四倍频1440Hz，减少了模态混叠影响，获得了更加清晰简易的信号数据。由此可见，利用本文方法进行设计获得的传动轴满足使用要求。

4 结语

1) 传动轴发生了局部振动并存在扭转，当模态阶数增大后，获得了更明显振型。传动轴前6阶频率介于625～1339Hz之间，并且最低固有频率也大于最高啮合频率，从而避免了齿轮箱与传动轴发生共振的问题。

2) 低频部分形成了故障频率等于360Hz的一倍、二倍频，同时获得了更明显的三倍、四倍频，可以判断本文方法能够大幅降低高斯噪声导致的低频弱故障概率。利用本文方法进行设计获得的传动轴满足使用要求。