基于ABB 机器人Rapid 编程语言的机器人轨迹规划研究

徐源东， 朱 攀， 林 琳

（云南省机械研究设计院， 云南省机电一体化应用技术重点实验室， 云南 昆明 650031）

0 引言

机器人的根本任务， 就是要实现从一个开始位置到一个目标位置的运动， 这就需要通过对复杂组合体进行规划来实现。 机器人的轨迹规划（Trajectory Planning），就是要为机器人从初始位姿移动到目标位姿， 通过指定一系列参数，找出一条无碰撞且可行（连续平滑）的路径，生成相关变量的时间律， 以描述期望的轨迹。 本文基于ABB 机器人Rapid 编程语言， 对机器人的运动学进行分析，进行了机器人轨迹规划的研究与计算。

1 机器人位置与姿态

1.1 机器人坐标系

轨迹规划的基本问题是将操作臂从初始位置移动到最终期望位置——即将工具坐标从当前值{Tinitial}移动到期望值{Tfinal}。 在工业机器人应用中，用工具坐标系{T}相对于工件坐标系{S}的运动来描述。在ABB 机器人中表示为TCP（工具中心点：带方向的点）相对于wobj（工件坐标系）的运动。

目前还没有国际统一的机器人坐标系标准命名，本文以ABB 机器人的命名方式为例， 将机器人运动的相关坐标系分为5 类坐标系，用以描述机器人的相关运动。 分别为：大地坐标系（World coordinates）、基座标系（Base coordinates）、 工具坐标系 （Tool coordinates）、 用户坐标系（User coordinates）和工件坐标系（Object coordinates）[1]。 各坐标系关系见图1。

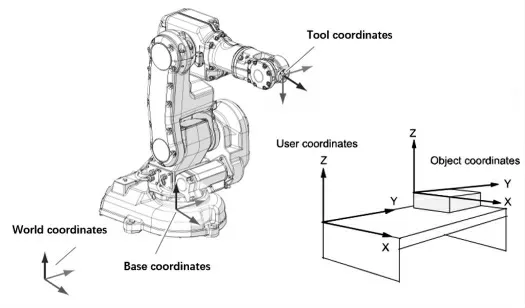
图1 机器人运动相关坐标系

1.2 机器人目标点位数据与工具姿态

1.2.1 ABB 机器人目标位置定义

ABB 机器人RAPID 程序中，用两种类型的数据描述机器人点位：

关节位置数据jointtarget 和TCP 位置数据robtarget。jointarget 记录的是机器人各个轴的绝对偏移位置；robtarget 记录的是机器人笛卡尔坐标系下的xyz 坐标及角度等数据。 两种指令格式分别见图2。

图2 两种类型的数据描述机器人点位

1.2.2 工具姿态描述

三维空间坐标系的姿态方向可通过基准坐标系的旋转来表示，姿态的表示方法有很多种，如旋转矩阵（标准正交阵）、转角排列设定法（X-Y-Z 固定角、Z-Y-X 欧拉角、Z-Y-Z 欧拉角）、轴角（等效角度-轴线）、四元数（欧拉参数）等。 在ABB 机器人RAPID 编程语言中，以四元数（Quaternion）描述和储存坐标系姿态。在实际应用项目中，常通过将四元数转化为欧拉角应用， 如视觉定位抓取项目中，获取产品的偏移角度后，通过获取标定目标点的欧拉角Z，对相应值进行计算后，对产品进行旋转定位抓取。

（1）Z-Y-X 欧拉角：

坐标系{B}的欧拉角表示方法如下：

首先将坐标系{B}和一个已知参考坐标系{A}重合。先将{B}绕ZB^ 转α 角，再绕Y^B转β 角，最后绕X^B转γ 角。这样三个一组的旋转被称作欧拉角[2]。

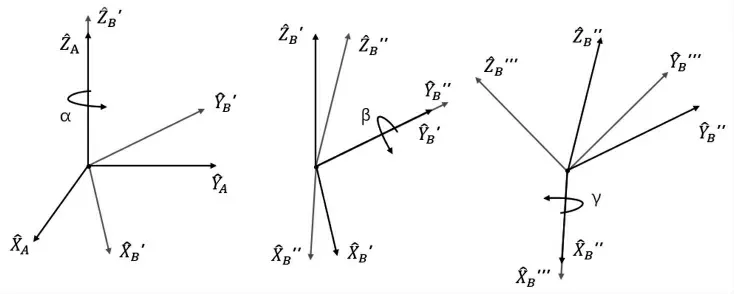
图3 Z-Y-X 欧拉角

（2）四元数：

在ABB 机器人RAPID 编程语言中，以四元数（Quaternion）描述和储存坐标系姿态，姿态数据类型是Orient，格式为[q1，q2，q3，q4]，四元数是带符号的常数，始终满足平方和等于1：

式中的（x1，x2，x3）、（y1，y2，y3）、（z1，z2，z3）分别为旋转坐标系X’，Y’，Z’轴单位向量在基准坐标系X、Y、Z 轴上的投影。

2 机器人运动学分析

2.1 机器人正运动学——D-H 表示法

D-H（Denavit-Hartenberg）表示法可用于表示任何机器人构型，也可用于表示任何坐标系中的变换，以及任何可能的关节和连杆组合。 对于6 轴垂直串联机器人的正运动学， 可以通过D-H 参数转化为各个轴的位姿矩阵，将6 个位姿矩阵右乘即可得到当前机器人末端TRP 的笛卡尔坐标。

机器人的正运动学就是在已知机器人结构参数的前提下，通过输入各关节的角度（即jointtarget 数据），就能计算出当前法兰盘（TRP）在固定坐标系（wobj）中的位置及姿态， 即通过关节数据jointtarget 求笛卡尔坐标数据robtarget。

图4 六轴机器人控制模型与结构参数

六轴机器人建模如上图，建立Base 坐标系（X0Y0Z0），之后依次对应1 轴到6 轴6 个坐标系（X1Y1Z1……X6Y6Z6），通过D-H 参数来表示这6 个动坐标系相对于前一个坐标系的关系（T1-T6）：

对于D-H 参数，旋转和平移顺序如下：先绕当前X轴旋转α 度，再沿新的X 轴平移a，再绕新的Z 轴旋转θ度，再沿新的Z 轴平移d。

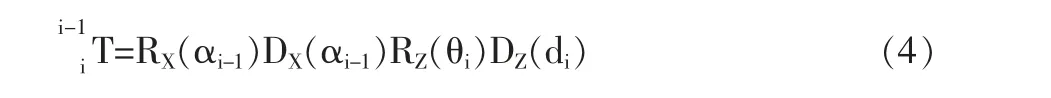
按上式计算整理后，可以得到基于D-H 参数的位姿矩阵如下：

品牌工业机器人的D-H 参数一般机器人生产厂家在系统参数中已做设置。 在ABB 机器人中，相关D-H 参数一般在系统模块（System moudle）中定义，在安装系统时已自动加载，不会受用户作业删除操作影响，可在DHParameter 内查看相关值。

TRP 是确定工具作业点、设定工具数据的基准位置。根据D-H 参数确定TRP 后，就可进一步设置工业机器人的工具作业点TCP（Tool Control Point），它是机器人关节、直线、圆弧插补等移动指令的控制对象，指令中的起点、终点就是TCP， 在指定坐标系上的位置值TCP 的位置与工具形状、安装方式密切相关。

在ABB 机器人的RAPID 编程语言中， 可直接使用CalcRobt 函数，将关节数据jointtarget 直接转换为笛卡尔坐标系数据robtarget，示例如下：

CalcRobT（j_ temp，tool1WObj：=wobj0）

2.2 机器人逆运动学

逆运动学问题是由给定的末端执行器位置和姿态，求解一系列满足期望要求的关节角。 逆运动学可分解为两部分：①进行坐标系变换求出相对于基座标系{B}的腕部坐标系{W}；②应用逆运动学求关节角。

在ABB 机器人RAPID 编程语言中，即已知robtarget笛卡尔坐标系的偏移值tran.（x，y，z）， 和姿态rot.（q1，q2，q3，q4），根据已有D-H 参数，求解关节偏移jointtarget 的解。目的是将分配给末端执行器在操作空间的运动，变换为相应的关节空间的运动，使得期望的运动能执行。

逆运动学相对于正运动学需研究以下问题：

（1）解的存在性：工作空间是机器人末端执行器所能到达的范围。 若解存在，则目标点必须在工作空间内。 常规品牌机器人在主要参数中会标注机器人工作半径，见图5。

图5 不同结构类型的机器人的工作空间

（2）多重解问题：多重解的问题不仅取决于自由度的数量，还取决于非零D-H 参数的个数。 通常，连杆的非零参数越多，可行解的越多。机械的关节限制有可能会最终减少在实际结构中多重可行解的数量[3]。

图6 为ABB 公司IRB14000 机器人， 单臂有7 个自由度，对于同一个目标位置点Target_960，共有5 种关节变量组合可到达目标位置。

在ABB 机器人的RAPID 编程语言中， 可直接使用CalcJointT 函数，将笛卡尔坐标系数据robtarget 直接转换为关节数据jointtarget，示例如下：

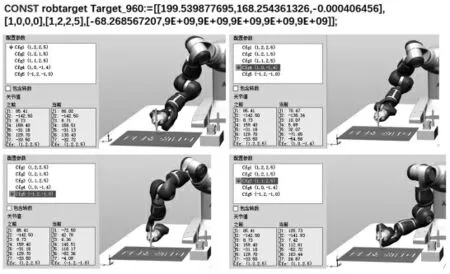
图6 IRB14000 的右臂对于同一目标点Target_960 的不同轴配置

CalcJointT（Target_10，tool1WObj：=wobj0）

3 轨迹规划

3.1 轨迹规划综述

路径与轨迹规划与受到控制的机器人从一个位置移动到另一个位置的方法有关。 用来指定并规划路径的方法有很多种。 任何在规定的时间里通过中间点的光滑函数都可以用来指定精确的路径形状。

路径 （Path）表示在关节空间或操作空间中，机械手在执行指定运动时必须跟随的点的构型序列，是纯几何描述。 轨迹（Trajectory）是一条指定了时间律的路径[4]。

轨迹规划算法的输入包括路径描述、 路径约束以及由机械手动力学施加的约束， 其输出是按时间顺序给出的位置、 速度和加速度的值构成的末端执行器 （TCP）轨迹。 轨迹规划算法生成一个描述末端执行器位置和方向变量依照约束随时间变化的时间序列。 在轨迹生成的运行时间内需要计算位置、速度和加速度。

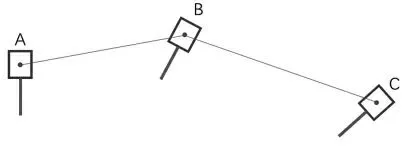
图7 机器人在路径上的依次运动

3.2 关节空间的规划方法——MoveJ

当以关节转角的函数来描述轨迹在空间和时间的轨迹生成时，通常将每个路径点用工具坐标{T}相对于固定坐标系{S}的期望位置和姿态来进行描述。

3.2.1 高次多项式

在一定时间将工具从初始位置移动到目标位置，应用逆运动学可以解出对应目标位置和姿态的各个关节角。各关节初始位置已知，需要确定每个关节的运动函数，t0时刻为该关节的初始位置，tf时刻为该关节的期望目标位置，用高次多项式作为路径曲线段，要确定在路径曲线段的起始点和终止点的位置、速度和加速度，采用一个五次多项式进行插值：

这些约束条件确定了一个具有6 个方程和6 个未知数的线性方程组，其解为：

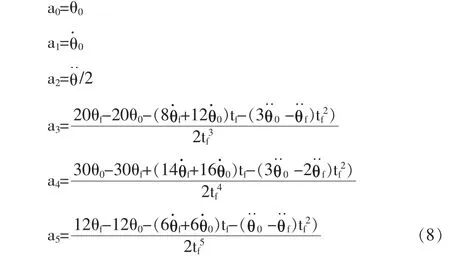
3.2.2 带抛物线过渡的线性函数用于经过中间点的路径

在工业机器人实际应用中， 从起始点到目标点常会设置过渡点，经过过渡点时，通常使用抛物线进行过渡，保证运动的平滑，减少震动，降低磨损。 在工业机器人应用中抛物线转角半径大小叫平滑度。

如图8， 在关节空间中位某个关节θ 的运动指定了一组中间点，每两个中间点之间使用线性函数相连，而各中间点附近使用抛物线过渡。

用j、k、l 表示三个相邻的路径点。位于路径点k 处的过渡区段的时间间隔为t_k。 位于点j 和k 之间的直线部分的时间间隔为tjk。点j 和k 之间总的时间间隔为tdjk。直线部分的速度为θ·jk， 而在点j 处过渡区段的加速度为θ··j，如图8 所示。

已知所有的路径点θk、期望时间区间tdjk以及每个路径点处加速度的模值|θ··k|，则可计算出过渡区段的时间间隔tk。 对于内部路径点，使用下列公式计算：

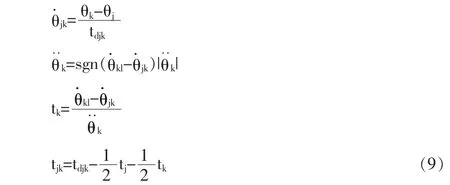
图8 多段带有过渡区段的直线路径

对于第一个路径段和最后一个路径段， 整个过渡区的持续时间都必须计入路径中， 所以对于第一个路径段，使线性区段速度的两个表达式相等来求解t1：

上式用于计算给定中间点及各个路径段的持续时间，求出多段轨迹中各个过渡区段的时间和速度。系统使用各个关节默认加速度值。

3.3 笛卡尔空间的规划方法——MoveL

让工具在相隔较远的中间点之间走直线运动， 这种执行路径的模式称作笛卡尔直线运动。在笛卡尔运动中，可以使用笛卡尔变量关于时间的任意函数来定义路径。

基于笛卡尔空间的运动规划中， 组合成轨迹的函数都是描述笛卡尔变量的时间函数， 每个路径点都是由工具坐标系相对于固定坐标系的期望位置和姿态来确定。路径点是由{T}相对于{S}来描述的，在运行时以实时更新路径的速度求出运动学逆解，在笛卡尔空间生成路径后，通过求解逆运动学来计算出期望的关节角度。

3.4 路径的实时生成

机器人在实时运行时，路径生成器不断产生用θ、θ·和θ··构造的轨迹，并且将相关信息传输到机器人控制系统。

3.4.1 关节空间路径生成

在直线区段，各个关节的轨迹计算如下：

3.4.2 笛卡尔空间路径生成

使用符号x 表示笛卡尔位姿矢量的分量， 重写式（14）和式（15）。 则在曲线的直线区段，x 中的每个自由度按下式计算：

t 是第j 个中间点算起的时间，而x·jk是在轨迹规划过程中由方程（9）求出。 在过渡区段中，每个自由度的轨迹计算如下：

4 结束语

本文基于ABB 机器人Rapid 编程语言，以ABB 机器人实际应用中的程序为例， 对6 轴机器人进行了运动学分析，进而对机器人轨迹规划进行了研究与计算，为机器人应用的轨迹规划提供了理论依据。