一种基于混沌云分流机制的大数据社会工作流自适应调度优化算法

杨齐成

滁州广播电视大学,安徽滁州,239000

随着云技术的不断发展，各种基于大数据流的调度适应方案层出不穷[1]。由于大数据社会工作流具有较强的混沌特性，需要通过双向方式对流的成本等进行基于一次核实机制成本核算，导致当前调度算法中存在时间收敛程度不高、费用高昂等问题，致使调度适应方案的使用受到一定程度的限制[2]。

为解决当前研究过程中的瓶颈性因素，研究者提出了若干大数据社会工作自适应调度优化算法，在一定程度上解决了部署过程中存在的问题。Thelwall[3]等提出了一种基于拉朗日自删除机制的大数据社会工作流自适应调度算法，通过随机加入拉格朗日校验因子的方式，能够实现大数据社会工作流的随机分配，且分配过程中缓存因子可进行自删除；然而，该算法需要在空间密度映射过程中进行一一比对，未考虑整体服务水平下降对算法收敛程度的影响，致使该算法的复杂度较高。Bal[4]提出了一种基于一体化成本控制机制的大数据社会工作流自适应调度算法，证明社会工作流的成本核算能够在可接受的范围内进行实时核算，且成本核算过程的收敛性较高，不过该算法主要采取固定控制的方式进行成本核算，流指数矢量的弹性性能不高，导致该算法在数据随机性较强的情况下极易出现严重的队列缓存无法得到及时更新的问题，降低了算法的可用性。 Mohammad[5]基于流缓存拥塞控制特性，提出采取随机映射方式实现算法整体负载的可用性提升，进而采取流缓存拥塞控制的方式提高算法的动态收敛效果；然而，该算法需要采取异构方式实现可用性重构，当工作流的参数为随机变量时，将由于频繁发生的缓存更迭导致出现鲁棒性下降的现象。

考虑到当前算法存在的不足之处，本文提出了一种基于混沌云分流机制的大数据社会工作流自适应调度优化算法。首先基于时间因子对流进行混沌云自演进结构构建，按段缓存实现流的自适应缓存衍射；随后采取逆向评估方式进行缓存分流，并使用分流效果最强的子流作为输出校验，因而改善了本文算法的收敛效果。最后采取NS2仿真实验环境进行了性能测试，证明了本文算法的优越性。

1 基于时间因子的流混沌云自演进结构构建

考虑到大数据社会工作流形成过程中，各种子流的上传及质量参数的保障均按其流维度进行了有效分割，因此相应的流结构具有很强的自迭代特性，能够按时间因子的方式进行结构重建[6]。当前算法均未能对该因素进行考虑，若算法实现过程中子流的上传及质量参数的保障出现波动，则难以通过迭代的方式对整体流进行演进评估，导致算法的收敛性严重下降；因此需要充分引入时间因子的方式，按段进行流维度分割评估，然后对分割后的密度矢量进行成本核算，并针对该核算过程进行二次优化，从而在提高算法收敛性的同时，降低整体控制成本，以便达到算法优化的目的。

1.1 整体算法步骤

对于任意时刻的大数据社会工作流而言，整个成本核算的优化过程能够使用演进结构重构、流维度分割、成本控制三个阶段[7]。因而，本文算法采取结构演进混沌度、分割成本、收敛成本三个性能指标，充分阐述混沌云分流过程，整体算法步骤如下：

(1)根据子流的概率分布，预先估计下一时刻子流的流维度及分型方式，然后根据成本最低原则进行云接入过程；

(2)对第一步中获取的子流进行自演进结构重建，然后基于接入成本最低原则进行二次接入，直到任意一条工作子流被处理完毕；

(3)完成第二步后，对工作子流按段核算，在自身维度范围内进行成本削除；

(4)本次流程结束后，云中的工作子流继续保持监听状态，直到全部的工作子流被处理完毕。

1.2 混沌云分流机制

根据上述步骤，整个混沌云分流机制分为如下两个阶段。

首先，依据单条工作子流的离散参量，按当前成本概率进行成本初次核算。由于工作子流在各个维度上均处于离散状态，且满足一定的随机分布特性，因此接入过程中其成本矢量均可按照粒度进行初次成本核算[8]。就时间因子t0而言，流的成本矢量由不断累计的粒度进行结构重建，且不同粒度的抵达均按照成本最低的方式实现迭代。故该过程满足t分布特性，且特征指数为λ，混沌云中各条工作子流彼此间也均满足t分布特性，其时间因子集合X满足相同的特制指数。另外，考虑到实际过程中各条工作子流均满足独立分布特性，因此混沌云分流过程中的成本函数MQ如下：

MQ=min(λE|X|-2,eλE|X2|)

(1)

其中，E|X|为一级平均成本指数，E|X2|为二级平均成本指数。

获取到混沌云分流过程中的成本函数后，还需要按段对不同的工作子流的时间成本进行核实，若该成本的分布概率也满足公式(1)，则说明该工作子流也将处于独立演进装；若该成本的分布概率不满足MQ，则需要对该工作子流进行演进结构构建，形成新数字特征MQ，并继续进行迭代，判断准则如公式(2)所示。

(2)

其中，1表示当前工作子流的新数字特征已经形成，可按照公式(1)所示继续进行下一时刻的数据分流；0表示当前工作子流的新数字特征尚未形成，需要继续实现演进结构构建。

其次，进行成本二次核算。由公式(2)确定当前工作子流的构建率p′是够可以进行演进结构构建，从而能够确保成本核算过程始终按照收敛程度最佳的原则进行。

考虑到公式(1)所示的成本函数MQ在整体核算期间均保持独立同分布状态，若各条工作子流也处于独立同分布状态时，则可以按照该成本函数对当前处理成本进行规范化正交[8]，如公式(3)所示。

(MQ)p′=MQ(x)

(3)

其中，成本函数的构建率p′满足参数为λ的泊松分布，其收敛指数x满足如下特性，如公式(4)所示。

(4)

虽然式(4)完成了成本函数的构建，然而该过程均处于离散状态，因此需要对处于离散状态的成本函数进行区间二次映射，令某条工作子流的成本函数p(x)，相应的数字特征为μ，则核算成功率p满足公式(5)。

p=minMQ(x)+maxMQ(x)

(5)

由于各条工作子流所处的混沌云空间Δ与核算成功率存在显著的正向波动关系[9]，因此可按照时间因子对该核算成本进行分段，令分段过程中的抽取周期为Δt，波动过程的成本特征Δs满足公式(6)-(10)。

(6)

考虑到Δ的强收敛特性[10]，可得：

(7)

故成本平均分布pnest满足:

(8)

(9)

据此可知，任意一条工作子流的成本plast均满足如下的表达式：

(10)

由上式即可获取整个混沌云空间的成本。

2 算法流程

由基于时间因子的流混沌云自演进结构构建内容，本文算法流程按如下步骤进行：

(1)首先进行工作子流的获取，按先来先处理的原则进行数据处理；

(2)对于任意工作子流而言，搜寻混沌云空间内全部可处理的粒度，处理完成之前，均按照公式(2)～(6)的方式进行成本核算，否则将继续接收抵达的粒度，直到全部的工作子流的粒度被处理完毕为止；

(3)按式(7)～(10)所示核算整个混沌云空间的成本；

(4)算法结束。

整个算法的流程图如图1所示。

图1 社会工作流自适应调度优化算法流程图

3 仿真实验

3.1 仿真环境设置

为评估本文提出的调度优化算法，仿真实验中使用NS-2仿真平台对共线度混沌粒子成本核算机制(Collinearity Chaos Particle Cost Accounting，3C_PA机制)[11]及一体化演进分度核算(Integrated Evolution Accounting，IEA机制)进行仿真对比。实验仿真参数如表1所示。

表1 仿真参数表

仿真实验中，为验证本文算法优越性，实验重点是从粒度处理密度、成本核算周期、粒度损失度、流粗度收敛率四个指标进行仿真对比。

3.2 结果分析

3.2.1 粒度处理密度

图2显示了不同流密度情况下本文算法与3C_PA机制及IEA机制在粒度处理密度上的对比，分析可知，随着流密度的不断增加，本文算法的粒度处理密度始终处于较高水平，而3C_PA机制及IEA机制的粒度处理密度较低，且波动情况要高于本文算法，这是由于本文算法采取混沌云分流机制，能够实现整体成本较低的情况下的粒度处理能力的提升，因此，在流密度不断增高的情况下，降低抵达的粒度对整系统的处理能力的影响，因而粒度处理密度较高，而对照组算法由于未考虑粒度抵达过程中的分布特性，当粒度密度不断增加时，其分布状况也将随着粒度密度的增加而出现显著的恶化现象，致使算法的粒度处理能力要低于本文算法。

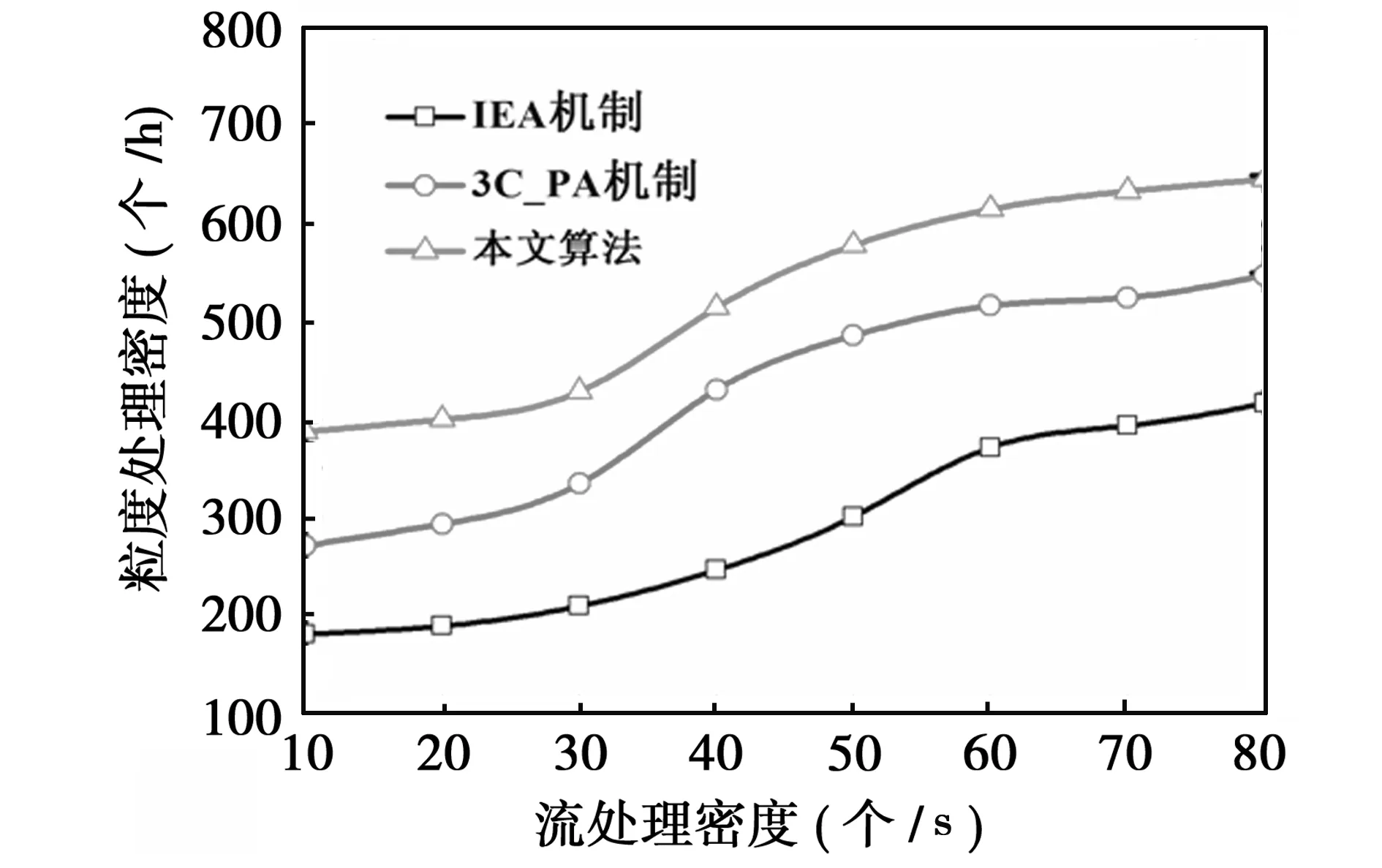
图2 粒度处理密度测试

3.2.2 成本核算周期

图3显示了在不同流密度情况下，本文算法与3C_PA机制及IEA机制在成本核算周期上的对比，由图可知，随着流密度的不断上升，本文算法的成本核算周期始终处于较低水平，而3C_PA机制及IEA机制的成本核算周期随着流密度的上升，其成本核算周期也不断上升；这是由于本文算法采用混沌云分流机制，能够采用段控制的方式降低成本核算过程中的复杂度，因此，在流密度不断提高的情况下，单位周期内的处理能力要远远高于3C_PA机制及IEA机制，因而成本核算周期较低；而对照组算法未充分考虑成本的二次核算，仅对当前抵达的流进行一次成本核算，因此在流密度不断上升的情况下，成本核算周期要高于本文算法。

图3 三种算法的成本核算周期测试

3.2.3 粒度损失度

图4显示了在不同流密度的情况下，本文算法与3C_PA机制及IEA机制在粒度损失度上的对比，由图可知，本文算法的粒度损失度要低于3C_PA机制及IEA机制，这是由于本文算法充分考虑了粒度的数字特征，采用段方式及分流方式对抵达的粒度进行实时处理，因此粒度等待时间处于较低水平，降低了因处理不及时而从缓存中删除的概率。而传统的3C_PA机制及IEA机制均采用简单的队列处理机制，一旦当前队列因处理能力所限而处于拥塞状态时，后发的粒度将需要等待下一时间周期方能得到服务，因此粒度损失度均要高于本文算法。

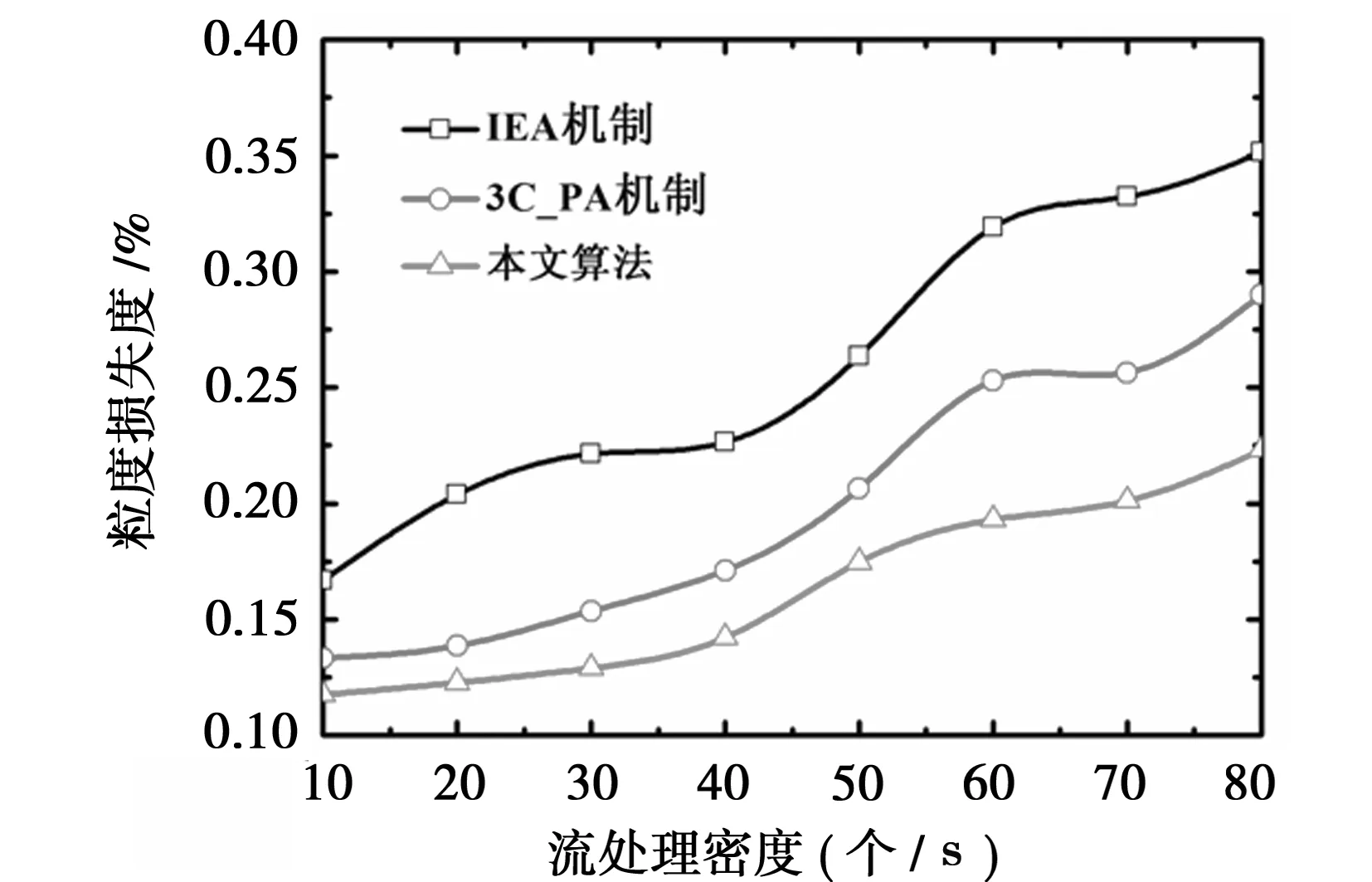
图4 各算法的粒度损失度测试

3.2.4 流粗度收敛率

图5显示了在不同流密度的情况下，本文算法与3C_PA机制及IEA机制在流粗度收敛率上的对比，由图可知，本文算法的流粗度收敛程度较快，流粗度收敛率要远远高于对照组算法，这是由于本文算法在分段过程中按粒度进行二次成本核算，通过公式(7)的方式对成本核算过程中的粒度进行了正规化处理，减少了因拥塞控制困难而导致的收敛不畅的现象；对照组算法由于采用单纯经济核算机制，当流出现收敛困难的现象时，其成本密度函数也呈现急剧上升的态势，导致核算失败，因此流粗度收敛性能较差。

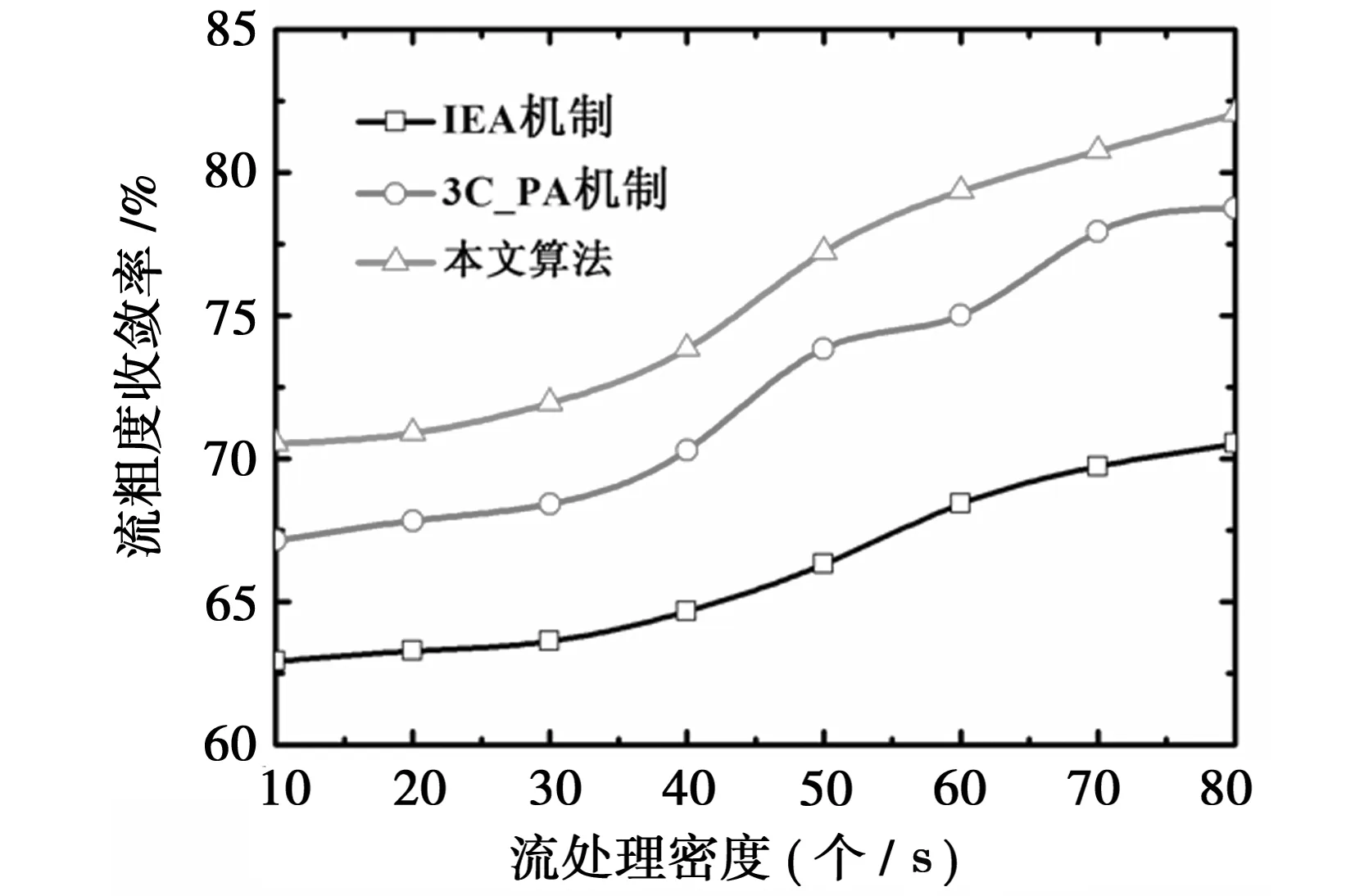
图5 不同算法的流粗度收敛率测试结果

4 结 语

针对当前大数据社会工作流自适应调度优化算法存在的费用较高、时间收敛性能不好、且成本核算质量较差等难题，提出了一种基于混沌云分流机制的大数据社会工作流自适应调度优化算法。首先通过时间机制将社会工作流按大数据方式进行数据建模，并据此进行混沌云分流且评估成本效果；随后根据成本效果逆向进行周期性能评估，能够有效地对工作流进行费用核算及性能提升，仿真实验证明了本文算法的有效性。