多矩阵低秩分解的鲁棒特征提取
米雪荣,王恒友,何 强,张长伦
(1.北京建筑大学理学院,北京100044;2.北京建筑大学北京未来城市设计高精尖创新中心,北京100044)
引 言
人脸识别拥有广泛的应用前景,如安防、金融支付和刑侦等。然而在实际应用中,无论是人脸识别分类算法,还是特征提取方法,对稀疏大噪声或野点噪声的鲁棒性仍面临一定的挑战,有待进一步提升。特别是传统的基于小样本的人脸识别方法,特征提取是其识别效果的关键。在众多特征提取方法中,一类利用数据间结构相似性进行特征提取的方法受到研究人员广泛关注,如:经典的主成分分析(Principal component analysis,PCA)[1]、线性判别分析(Linear discriminant analysis,LDA)[2]以及局部保留投影(Locality preserving projection,LPP)[3]等。然而,该类基于L2范数近似误差最小化的特征提取方法仅对无噪声样本或含高斯噪声样本有较好的特征提取效果[4],对含稀疏大噪声或野点噪声的样本很难达到预期效果。
为了解决特征提取对稀疏大噪声或野点噪声的鲁棒性问题,研究者们采用的方法主要有两类。一类在传统的特征提取方法基础上构建稀疏大噪声鲁棒正则化项。例如,由于L1范数是L0范数的凸松弛,可以很好地度量稀疏大噪声的浓度,Kwak等[5]为了提取图像的特征,在PCA算法的基础上加入了L1范数;Ding等[6]提出了旋转方差不变性的PCA方法提取特征;Qiao等[7]在特征提取时加入了投影矩阵,能够更好地探索数据在低维空间的结构。该类方法对稀疏大噪声或野点噪声均具有很好的鲁棒性。另一类去除稀疏大噪声或野点噪声影响的方法是探索数据空间的低秩结构,该类方法通过探索数据之间的结构信息提取数据空间的低秩结构特征,从而达到降低数据维度的目的。Wright等[8]提出了基于低秩矩阵恢复(Low⁃rank matrix recovery,LRMR)的人脸重构方法,该方法充分利用人脸之间的结构相似性,并将秩函数凸松弛为核范数探索人脸库的低秩结构。此外,考虑到传统低秩矩阵理论在构造大尺度矩阵时需要将每个样本拉成列向量,容易破坏人脸矩阵的二维结构特征,Ye[9]提出了广义低秩矩阵(Generalized low⁃rank matrix,GLRAM)的图像近似算法。由于该方法仍然采用L2范数最小化度量近似残差,故对稀疏大噪声或野点噪声较敏感。随后,针对GLRAM的不足,Shi等[10]提出了基于L1范数最小化的鲁棒广义低秩矩阵近似(Robustness GLRAM,RGLRAM),可以较好地恢复低秩分量与稀疏分量,提升了算法对稀疏大噪声的鲁棒性。然而,以上两种算法只考虑让近似误差最小化,忽略了近似矩阵的秩对其结果的影响。针对上述两种低秩近似模型的不足,Wang等[11]将近似矩阵的秩结构融入到优化目标函数中,进一步提升了人脸图像集或相似图像集的低秩逼近效果。
在人脸识别算法的研究方面,研究者们也在不断探索对稀疏噪声或野点噪声具有鲁棒性的分类方法。近些年,随着稀疏表示理论研究的不断深入,基于稀疏表示的分类(Sparse representation classifica⁃tion,SRC)方法受到学者们的广泛关注。由于采用样本之间的相似性作为度量标准,相比传统的基于欧式距离最近邻的分类方法,该类基于稀疏表示的分类方法对稀疏噪声具有较好的鲁棒性。Wright等[12]提出了基于稀疏表示的鲁棒人脸识别方法,该方法首先依据训练样本库中的人脸来构造字典,进而求解待测样本在该字典下的稀疏表示系数并实现样本分类。Yang等[13]研究了基于稀疏表示的Metaface算法,该算法从原始训练样本中的每个类别分别学习一组子字典,以提升算法效率。Jiang等[14]研究了基于K⁃SVD的字典训练方法,并将标签信息与字典的原子相关联,使得字典具有结构性。Zhang等[15]提出了判别性的K⁃SVD字典训练算法,提升了字典的完备性。此外,为了进一步提升稀疏表示分类算法的效果,探索更具鲁棒性的特征提取方法,Ma等[16]提出了低秩字典学习算法,通过最小化每类子字典的秩来分离图像中的干扰。Chen等[17]研究了基于判别低秩矩阵的稀疏表示人脸识别方法,通过低秩投影矩阵将受损的训练样本映射到低秩空间,进而构造出低秩空间的完备字典。Tang等[18]通过低秩矩阵理论对训练样本进行低秩与稀疏分解,并分别在低秩空间和稀疏空间对测试样本进行稀疏编码。以上算法都是对训练样本分离了干扰,所以构造出的字典对噪声及遮挡具有鲁棒性。王志强等[19]提出了加权判别稀疏保留投影方法,通过样本权值和最小化类内距离来提升分类效果。Huang等[20]通过构建恰当的投影矩阵,使得来自同类的样本投影在同一平面。Du等[21]给出了局部约束自适应正则化特征提取方法,增强测试样本与训练样本之间的局部相似性特征。
鉴于上述稀疏表示分类的良好性能以及低秩矩阵理论对高维数据良好的结构探索能力,本文主要研究基于低秩矩阵分解的特征提取方法,将鲁棒广义低秩矩阵分解模型应用于人脸识别低秩特征提取,也可称为多矩阵低秩分解(Multi⁃matrix low⁃rank decomposition,MMLR)方法。首先,在人脸训练集上,根据人脸集的结构相似特征训练出可分离的低秩特征投影矩阵;其次,结合获得的可分离低秩特征投影矩阵,建立测试样本的低秩特征提取优化模型,提取测试样本的低秩特征;最后,运用PCA方法进一步降低特征维度并采用稀疏表示方法进行分类。实验表明,与传统的特征提取方法相比,本文MMLR方法对椒盐噪声具有较好的鲁棒性,特别是噪声浓度较大时MMLR方法的优势更加明显。
1 相关工作
1.1 低秩矩阵恢复
在实际应用中,观测数据矩阵D∈Rm×n往往具有一定的近似低秩结构(或者可以根据观测数据构造出近似低秩矩阵)。为了探索数据的低秩结构,可将矩阵D做如下分解为

式中:A为低秩部分,E为稀疏部分。则式(1)可转化为如下优化问题,即

优化问题(2)的求解是NP难问题[8],很难直接求解。然而,由于矩阵核函数是矩阵秩的包络,矩阵的L0范数在一定条件下与矩阵的L1范数等价,可以将上述优化问题(2)凸松弛为

式中:‖A‖*为矩阵A的核范数,即矩阵A奇异值之和。
1.2 鲁棒广义低秩矩阵近似
传统的低秩矩阵近似主要针对单矩阵进行分解,在实际应用中往往需要通过将多个小矩阵拉成列向量,进而构造出单个大尺度矩阵再进行低秩分解。这不仅容易破坏原矩阵的二维结构信息,而且大尺度矩阵的低秩分解计算复杂度将急剧增加。鲁棒广义低秩矩阵近似直接对多个小矩阵进行低秩近似,无需将每个小矩阵拉成列向量,从而提升了低秩近似的性能。该方法通过对每个小矩阵进行三因子分解,并最小化近似误差,实现多个小矩阵同时低秩近似。即对给定的K张图像进行如下分解,即

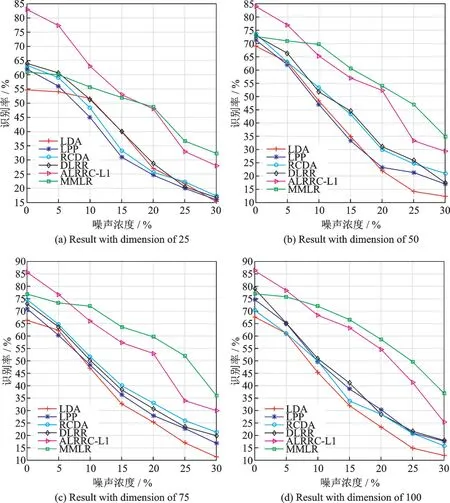
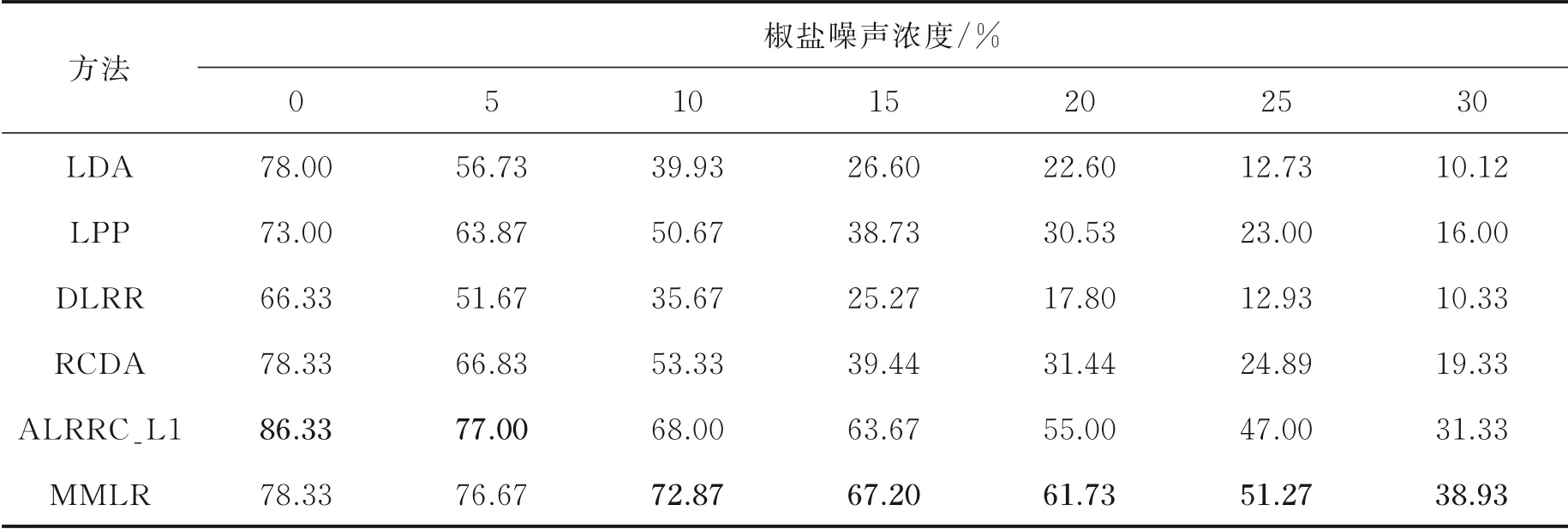
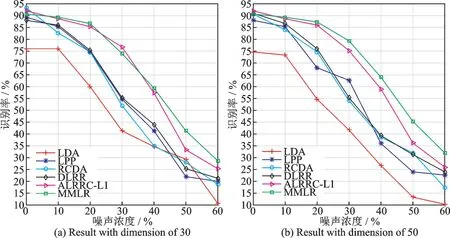
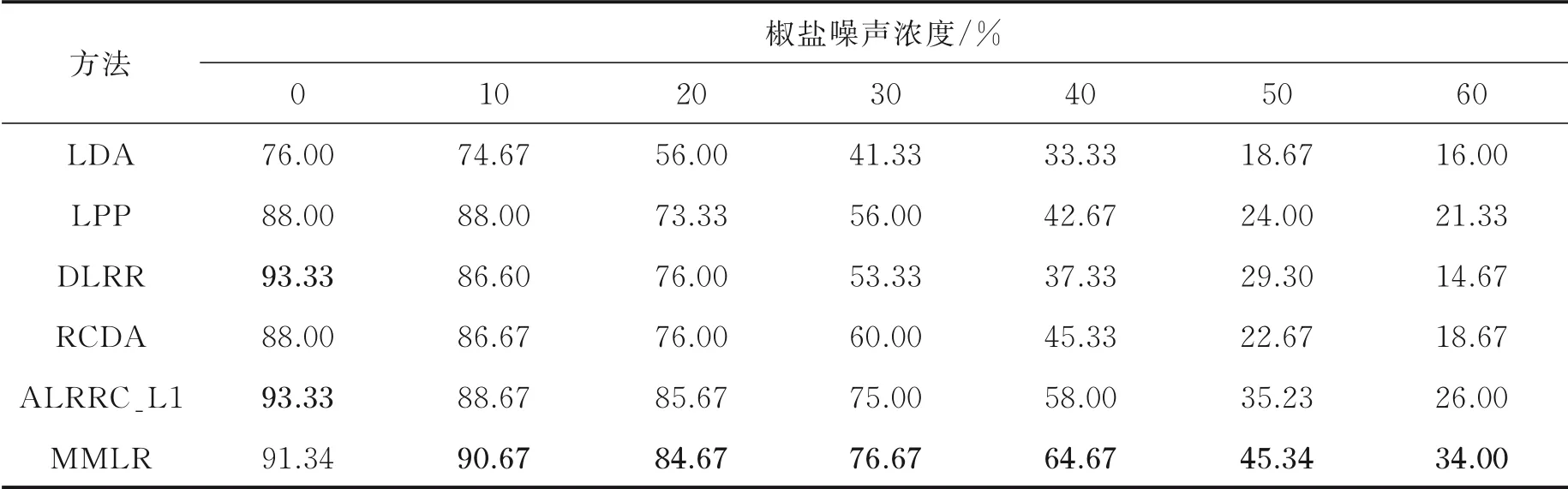
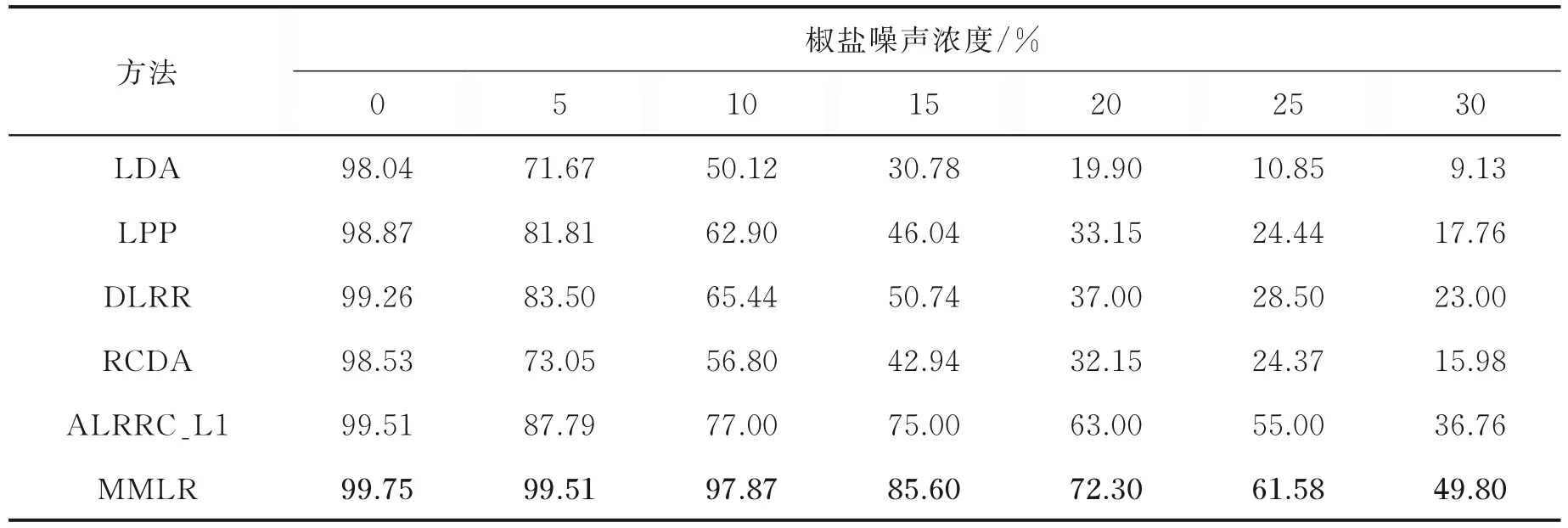
式中:L∈Rk×r1和R∈Rl×r2分别为列正交矩阵;M i∈Rr1×r2且max(r1,r2) 式中:I r1为r1×r1单位矩阵;I r2为r2×r2单位矩阵。若令D i=LM i RT+E i并代入式(5),则式(5)可转化为 式中E i代表稀疏误差矩阵。 稀疏表示分类通过求解L1范数最小化问题,将测试样本表示为训练样本所构造字典的线性组合,并利用稀疏表示系数及字典计算重构误差,进而对测试样本分类。具体阐述如下:令X=[X1,X2,…,X N]为N类训练样本构成的字典,其中X i=[X i1,X i2,…,X in]∈Rm×n代表第i类的n个样本,i=1,2,…,N。任意给定测试样本y∈Rm,可通过求解如下优化问题得到其稀疏表示系数,即 式中:a∈Rn为y在字典X=[X1,X2,…,X N]下的稀疏表示向量;β>0为平衡参数。最后,通过求解Identity(y)=arg miin ‖y-X i a i‖2,计算测试样本在各个训练类别下的残差,得到分类结果。 由于多矩阵低秩分解不需要将每个小矩阵拉成列向量,从而在探索其低秩特征时可以很好地保留其空间二维结构信息。本节将结合人脸识别案例,描述基于多矩阵低秩分解的特征提取方法。首先,针对人脸训练库,构造多矩阵低秩分解模型,探索人脸训练库的低秩子空间并提取特征矩阵。其次,运用训练样本库得到的特征投影矩阵,构造测试样本低秩子空间特征提取优化模型,获取测试样本的鲁棒特征。最后,利用PCA方法对所提取特征进一步降维,并运用稀疏表示方法进行分类识别。 设人脸图像库中包含N类不同人脸样本每类人脸含有n个训练样本[D i1,D i2,…,D in],则该人脸训练库中共包含K=nN个人脸样本。将人脸样本D ij∈Rk×l分解为D ij=A ij+E ij,i=1,2,…,N,j=1,2,…,n,其中A ij为低秩矩阵,E ij为稀疏矩阵;同时,对低秩矩阵A ij进行三因子分解,即A ij=LM ij RT,则多矩阵低秩分解可描述为如下优化问题,即 根据式(8)构造增广拉格朗日函数 使用增广拉格朗日乘子法(Augmented Lagrange method,ALM)[22]求解优化问题(9),即可得到训练样本的特征矩阵{M ij∈Rr1×r2}以及可分离特征投影矩阵L与R,并将每个特征矩阵M ij拉成列向量M ij(:),构造M={M ij(:)}。文献[11]列有详细求解过程。 利用已有的训练集迭代得到的低秩特征投影矩阵L与R,以及对测试样本H∈Rk×l进行低秩恢复,则测试样本的特征提取可表示为如下低秩矩阵恢复问题,即 式中:矩阵M H∈Rr1×r2为测试样本H经过式(10)中的低秩矩阵恢复模型所获得的特征矩阵。通过ALM算法即可求出(10)的最优解,构造如下拉格朗日函数,有 式中:Y代表拉格朗日乘子;μ>0为惩罚参数。根据ALM算法,求解矩阵M H,E以及Y的迭代更新公式可描述为 令H-LM H RT+Y/μ=Q∈Rk×l,则式(12)有最优解E*=ςλ/μ(Q),其中算子ςλ/μ(∙)为迭代收缩阈值算子,其第(i,j)元素为max(|qij|-λ/μ,0)sgn(qij)且λ/μ>0[4]。令H-E+Y/μ=S∈Rk×l,则式(13)有闭形式解其中ψ1/μ(LSRT)=Uς1/μ(Σ)VT,UΣVT为矩阵LSRT的奇异值分解[23]。经过上述公式的不断迭代,即可得到满足条件的矩阵M H,E以及Y。 综上,本文MMLR方法特征提取及人脸识别的步骤如下。 输入:D ij∈Rk×l(i=1,2,…,N;j=1,2,…,n),λ>0,β>0,max iter,r1,r2,H∈Rk×l。 初始化:A=E=0m×n,M H=0r1×r2,μ=10-4,ρ=1.1,η=108,iter=0。 步骤1训练样本库低秩子空间探索ALM求解式(9),得到M={M ij(:)},L,R。 步骤2测试样本特征提取 首 先,为 了评 价 本文MMLR方 法的 性 能,将 其与LDA[2]、LPP[3]、DLRR[17]、RCDA[20]和ALR⁃RC[21]5种方法进行比较。其次,为了验证MMLR方法的精度,分别在AR、Yale和CMU_PIE人脸库上进行实验,并将3个人脸库的样本尺寸下采样为32像素×32像素。为了保证与其他方法对比的公平性,本文从人脸库中随机挑选训练样本,将剩余样本作为测试样本。此外,调整每个算法的参数,以保证达到其最优精度。本文算法中特征矩阵M的大小取决于r1和r2的值。通过实验发现,当r1=r2=20,β=0.001,0.2<λ<1.2时效果最佳。实验结果为5次试验后得到的平均识别率,实验软件环境为Matlab R2014b。 AR人脸库包含关于126个人的4 000多幅正面图像,每个人的图像都是关于光照和表情等细节变化。实验中随机挑选25组男性,25组女性志愿者的图片,每一名志愿者有26张图片,其中包括14张无遮挡、6张戴眼镜和6张戴围巾的图片。将其均分为训练组与测试组,训练组与测试组中分别由7张无遮挡、3张戴眼镜以及3张戴围巾的图片组成。图1为AR人脸库中1名志愿者的全部图片。在训练组和测试组中分别随机选6张图片(其中包括4张无遮挡,1张带眼镜及1张戴围巾的图片),并依次加入浓度范围为5%~30%的椒盐噪声(图2)进行训练和测试。图3是维度分别为25、50、75及100的实验结果,表1是维度为150的实验数据。 从上述实验结果可以发现,随着特征维度增加,每个算法的识别率都在不断提升;而随着椒盐噪声浓度的增加,算法的识别率在逐渐下降。当椒盐噪声浓度达到10%~30%时,本文算法与其他算法相比识别率都最高。而根据表1可以直观地看出:当维度为150且椒盐噪声浓度在0%~5%时,本文MMLR方法的识别精度低于ALRRC方法;当椒盐噪声浓度高于5%时,MMLR方法的性能明显优于其他方法,说明椒盐噪声干扰越强,越能体现MMLR方法对椒盐噪声的鲁棒性;当样本中椒盐噪声达到30%时,MMLR方法的精度比ALRRC方法提升7.6%。 图1 AR库下采样的样本(第1行为训练组,第2行为测试组)Fig.1 Images in AR dataset(The first line is training group and the second line is test group) 图2 AR库样本依次加入5%、10%、15%、20%、25%及30%的椒盐噪声Fig.2 AR samples with 5%,10%,15%,20%,25%and 30%pepper and salt noise 图3 AR库特征提取+PCA降维实验对比图Fig.3 Feature comparison of AR dataset feature extraction with PCA dimension reduction experiment 表1 AR库特征提取+PCA降维至150的实验数据Table 1 Exper imental data of feature extr action of AR dataset with PCA r educed dimension to 150 Yale人脸库中包含15位志愿者的图片,其中每个人有包含表情、神态及光照下的11张人脸图片,共计165张图片。实验中,对样本依次加入浓度范围为10%~60%的椒盐噪声,并随机挑选6张图片进行训练,其余图片进行测试。图4是Yale人脸库中样本分别加入10%~60%的椒盐噪声的图像。当维度分别为30和50时对比结果如图5所示;当维度为40及60的实验数据如表2和表3所示。 从以上实验结果可知:在Yale人脸库中,样本中不加椒盐噪声或者椒盐噪声浓度比较小时,MMLR方法的识别率并不突出;但当样本中椒盐噪声浓度达到30%~60%时,MMLR方法的识别率与其他方法相比精度最高。此外,固定了椒盐噪声浓度,对维度进行探究,在样本中加入30%的椒盐噪声,并随机选取6张图片进行训练,其余图片进行测试,结果如表4所示。由表4可知,当维度高于36时,MMLR方法的识别率优于其他方法。 图4 Yale库下采样的样本依次加入10%、20%、30%、40%、50%及60%的椒盐噪声Fig.4 Yale samples with 10%,20%,30%,40%,50%and 60%pepper and salt noise 图5 Yale库特征提取+PCA降维实验对比图Fig.5 Feature comparison of Yale dataset feature extraction with PCA dimension reduction experiment 表2 Yale库特征提取+PCA降维至40的实验数据Table 2 Exper imental data of feature extr action of Yale dataset with PCA r educed dimension to 40 表3 Yale库特征提取+PCA降维至60的实验数据Table 3 Experimental data of feature extraction of Yale dataset with PCA reduced dimension to 60 表4 Yale库样本添加椒盐噪声浓度为30%的实验数据Table 4 Experimental data of Yale sample added 30%salt and pepper noise CMU_PIE人脸库中包括68位志愿者的图片,包含每个人的13种神态、43种光照变化以及4种表情下共计4 080张图片。实验中随机选取了34位志愿者,且每位志愿者包含24张图片(图6),在样本中依次加入浓度范围为5%~30%的椒盐噪声(图7)。随机选取12张图片进行训练,将剩余图片进行测试,实验结果如图8所示,表5显示了维度为160的实验数据。结果表明,在CMU_PIE人脸库中,当维度小于130且样本中包含椒盐噪声时,MMLR方法的识别率优于其他方法;当维度为160时,即使样本中不包含椒盐噪声,MMLR方法的识别率也最高,进一步验证了MMLR方法对椒盐噪声的鲁棒性。 图6 CMU_PIE人脸库样本Fig.6 CMU_PIE face library samples 图7 CMU_PIE库样本依次加入5%、10%、15%、20%、25%、30%的椒盐噪声Fig.7 CMU_PIE library added with 5%,10%,15%,20%,25%and 30%pepper and salt noise 图8 CMU_PIE库特征提取+PCA降维实验对比图Fig.8 Feature comparison of CMU_PIE library feature extraction with PCA dimension reduction experiment 表5 CMU_PIE库特征提取+PCA降维至160的实验数据Table 5 Exper imental data of CMU_PIE feature extr action with PCA r educed dimension to 160 本文将低秩矩阵恢复与鲁棒广义低秩近似算法相结合,对训练样本分解从而将其投影到低秩子空间中,利用得到的投影矩阵对测试样本进行特征提取,继而再结合PCA降维、稀疏表示分类得到分类结果。实验结果表明:随着椒盐噪声浓度以及特征提取维度的变化,本文方法相比于其他方法识别率均最高,验证了本文方法对椒盐噪声具有一定的鲁棒性。
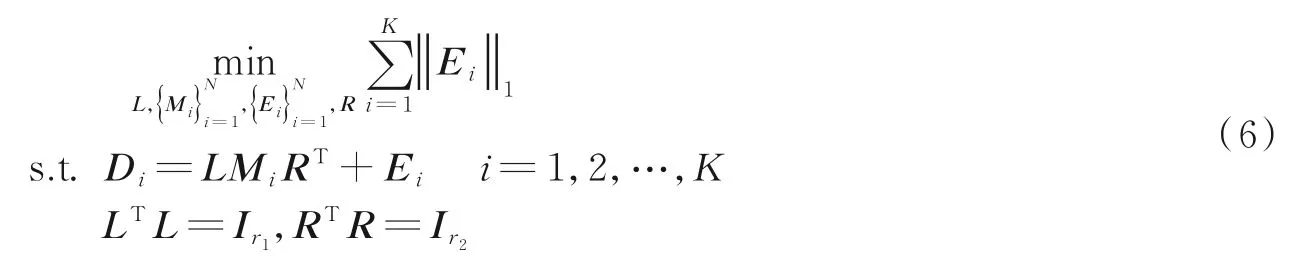
1.3 稀疏表示分类

2 多矩阵低秩分解特征提取
2.1 训练样本特征矩阵提取


2.2 测试样本特征提取

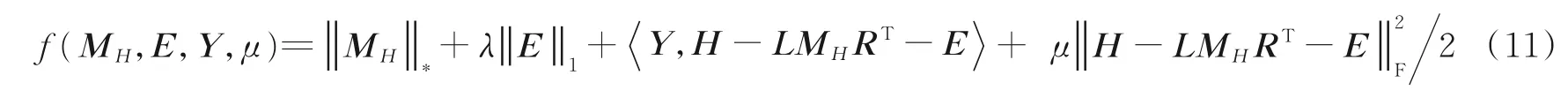



3 实验结果及分析
3.1 AR人脸库实验结果


3.2 Yale人脸库实验结果



3.3 CMU_PIE人脸库实验结果



4 结束语

