基于深度学习的时空序列预测方法综述
潘志松,黎 维
(陆军工程大学指挥控制工程学院,南京210007)
引 言
近年来,随着计算机软硬件技术的快速进步,如全球定位系统(Global positioning system,GPS)[1]和互联网[2]的发展、各类传感器和大容量存储设备的出现,包含地理位置信息的序列数据不断累积。传统的数据挖掘方式难以应付各领域时空序列数据[3]的爆炸性增长,因而亟需探索新的数据挖掘算法来应对规模不断增长的时空序列数据。时空序列数据通常是指具有空间相关关系的时间序列的集合[4],图1为东北三省自2001年来18年的居民人均地区生产总值时空序列示意图。
依据已采样的历史时空数据来预测未来某些时刻被观测的时空变量的值的过程被称为时空序列预测[4]。时空序列预测被广泛应用于多个领域,如交通规划[5⁃7]、天气预测[8⁃10]、经济统计分析[11⁃13]和农业产量预测[14⁃15]等领域。从多个角度挖掘出数据中蕴含的时空特征,精准地对时空变量进行预测能有效地为公共管理和个人规划等提供有效的决策和建议,具有重要经济价值和意义。
时空序列数据包含时间、空间和属性3个维度的信息[16],较为复杂。进行时空序列预测时不仅需要考虑不同时刻间的关联,还需要考虑不同位置在空间上的相互影响,并且这些时空关联往往是动态变化的[17],这给时空特征的挖掘带来了极大的挑战。现有的时空序列预测方法可大致分为两类:一是基于参数模型的传统的预测方法;二是基于数据驱动和深度学习的预测方法[18]。前者主要包含历史平均法[19](History average model,HA)、差分自回归移动平 均 法[20](Autoregressive integrated moving average mod⁃el,ARIMA)、时空差分自回归移动平均法[21](Spatio⁃tem⁃poral autoregressive integrated moving average model,STARIMA)、向量自回归法[22](Vector autoregressive mod⁃el,VAR)、决策树法[23⁃24](Decision tree model,DT)、隐马尔科夫模型法[25⁃26](Hidden Markov model,HMM)和高斯过程方法[27⁃28](Gaussian process model,GP)等。后者则依据时空数据的类型可分为面向网格数据的预测方法、面向图数据的预测方法以及面向轨迹数据的预测方法。

图1 东北三省近18年人均地区生产总值时空序列示意图Fig.1 Schematic diagram of the spatio⁃tempo⁃ral sequence of per capita GDP in the three northeastern provinces in the past 18 years
历史平均法对时空变量在历史时刻的观测值进行了平均,将均值作为预测结果。此种方法实现简单,但缺乏对时空数据特征的深层次挖掘,在实际应用中往往精度不高;差分自回归移动平均法将时空序列看成多条相互独立的时间序列分别进行预测,然而该模型忽略了时间序列之间的空间关联;时空差分自回归移动平均法虽然考虑了时空关联,但是对于非平稳的时空序列预测效果不佳;向量自回归法是由单变量自回归模型(Autoregressive model,AR)拓展而来,将时空序列视为多维时间序列然后预测,但该模型所需参数较多,需要大量样本;决策树法利用滑动窗口分解,将时空序列预测问题分为一系列固定长度的子问题分别进行预测,该方法无法捕获时空特征的动态变化;隐马尔科夫模型法主要是在时空密度聚类算法ST⁃DBSCAN[29⁃30]的基础上引入了时间维度,从而将时空序列预测转化状态预测问题,该方法假设条件过强,只适合特定的时空数据,泛化性能较低。高斯过程方法主要是通过计算数据的预测后验分布来得到预测值,如果观测的数据模型是非高斯模型,则还需要利用拉普拉斯近似来模拟后验分布。但高斯过程方法十分依赖于高斯核的选取,并且计算代价和空间复杂性都很高。
传统的预测方法在处理非线性、非平稳的时空序列预测问题中往往难以捕获动态的时空特征,在面对规模与日俱增的时空数据时后继乏力。近年来,基于数据驱动的深度学习方法在计算机视觉[31⁃32]、自然语言处理[33⁃34]、语音识别[35]和推荐系统[36⁃37]等大部分领域取得了惊人的进展。在时空序列预测领域,基于深度学习的预测方法往往也强于传统的方法,在处理动态变化的场景和长期预测问题上更是具有压倒性的优势。因此,本文主要研究对象是基于深度学习的时空序列预测方法。时空序列数据大致可分为以下3种类型:网格数据、图数据和轨迹数据,因而从数据类别的角度出发可以将对应的深度学习预测算法分为对应的3大类。
本文将从时空序列预测的需求入手,从时空序列的数据特点及其应用、基于深度学习的时空序列预测方法、时空序列预测中存在的难点和未来的研究方向这3个方面出发,系统地分析该领域的发展现状和未来研究方向。
1 时空序列数据特点及实际应用
1.1 数据特点
时空序列数据是在多个区域内对一个或多个研究对象动态变化过程的采样所获得的信息,反映了多个区域内变量随时间不断变化的趋势。其主要包含时间信息(采样的时间戳)、空间信息(采样的地点区域)和属性信息(观测的值,如流量、速度、方向、次数等)。时空序列数据可以通过含定位功能的移动智能设备(手机、智能手表、智能手环等)、GPS设备、打卡点、社交媒体、监控摄像头和站点传感器等方式获取,其来源广泛,复杂多样。广义的时空序列数据中的空间不仅包括物理空间,还包括逻辑空间、网络空间等。
表1列出了6种不同类型的典型时空序列数据集。这些数据集需要经过一系列预处理[38](筛选、去重、填充、重采样、去噪和变换等)之后才能应用于特定的预测模型之中。由表1可知时空序列具有海量性[3]、多样性和实时性,此外时空数据还具有以下特点:
(1)动态性。时空序列数据是一系列带有位置信息和时间戳的采样点序列,序列内部蕴含的特征会随时间不断变化,这给预测增加了许多难度。
(2)时空相关性。时空序列数据在时间维度和空间维度并非是独立的,而是会相互影响。不同位置的时间序列会相互影响,同一位置的序列在时间维度上也有着时序关联。
(3)数据噪声多。由于数据来源的多样化,时空序列数据往往存在很多噪声。例如不同设备采样的精度可能不一样、采样的时间维度难以完全对齐、采样的数据类别可能存在一定的不平衡等。
总而言之,时空序列数据广泛存在于现实生活的各个领域,在研究时空序列预测问题中必须充分考虑其特征并对其进行相应的处理,这样才能挖掘出其中的有用信息进而得出准确的预测结果。
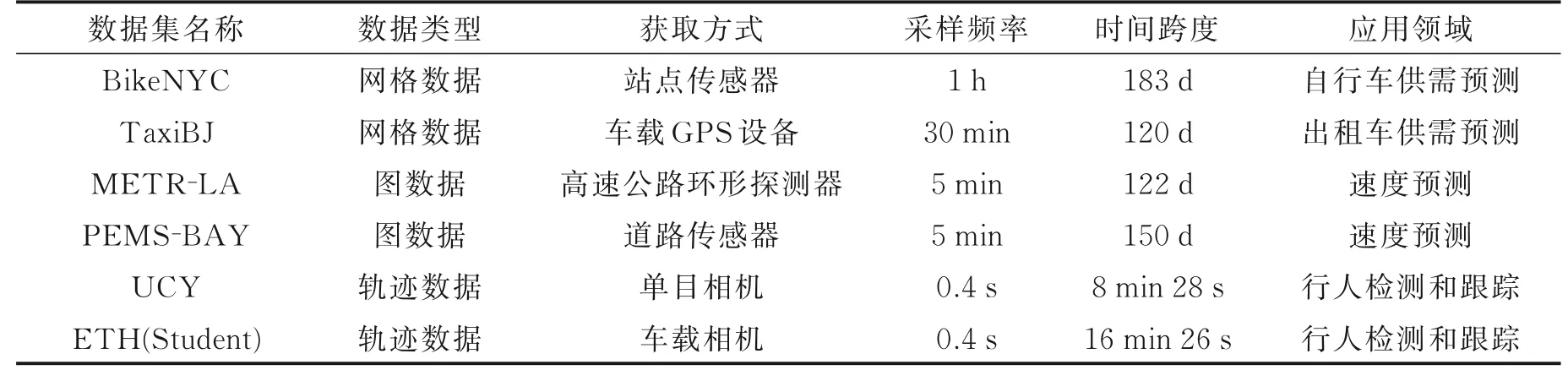
表1 6种代表性的时空序列数据集Table 1 Six representative spatio‑temporal sequence datasets
1.2 实际应用
时空序列数据中蕴含大量的信息,通过对其进行建模分析和预测,准确挖掘出这些信息能够有效地辅助人们科学决策、促进产业精细化管理,便捷人们日常生活。如图2所示,时空序列预测问题已经广泛应用在天气预报、出行安排、供需调配、产量预估和股市决策等方面,深刻地影响着人们的生活方式。
(1)天气预测。天气预测问题是一个复杂而具有挑战性的问题,准确预测天气对农业生产、工业和交通等领域有着极大的意义。在历史的天气数据中包含了丰富的信息,通过挖掘历史气候数据中潜在的规律,在结合最近的天气情况,可以对未来一段时间内的天气进行预测,为人们提供预警,有助于指导人们的生产生活。
(2)出行安排。随着交通的快速发展,人们的出行频率越来越高,但复杂的交通路况也使得人们难以预知自己的出行时间。通过对历史出行数据的挖掘,可以获取到不同路段在不同时间以各种方式通行所花费的时间,进而为人们出行的决策(是否出行、以何种方式何时出行等)提供参考。
(3)供需调配。出租车是人们出行的重要交通工具之一,然而很多时候人们都面临着打车困难的问题。通过对以往的出租车在不同位置的供应量和需求量数据进行挖掘分析,找出不同时刻不同位置出租车供需的变化规律。这样能够对出租车的调度进行优化,对其进行合理的分配调度,进而能有效提高用户的打车概率,减少出租车的平均空置等待时间。
(4)产量预估。粮食安全是我国的核心战略之一,准确预估粮食产量能够有效地避免风险,进而提早作出决策,掌握粮食生产的主动权。依据历史的产量和环境等数据对粮食产量进行预测,并和实际产量对比进行分析,也能够更快找出粮食增产或减产的主要原因,对指导粮食生产具有重要意义。
(5)股市决策。股票市场的预测是一个非常难的研究课题。将时空序列预测方法引入到股票预测之中,将不同的股票视为不同的节点进而构建预测模型,能够有效地挖掘出股票之间的联系,使得预测结果更加符合市场实际变动。
时空序列预测的应用并不仅仅局限于上述领域,随着各种定位技术和数据采集技术的发展,人们对时空序列数据挖掘的需求不断增高,其应用领域也会随之不断拓展。
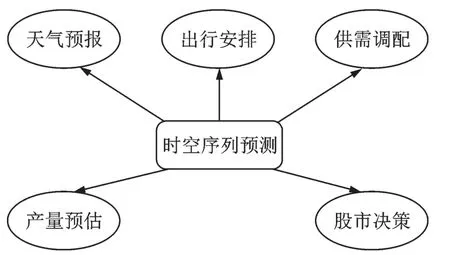
图2 时空序列预测的应用Fig.2 Applications of spatio⁃temporal se⁃quence prediction
2 基于深度学习的时空序列预测方法
近年来深度学习得到了蓬勃的发展,并且在多个领域取得了令人惊叹的成果。将深度学习引入时空序列预测中,能够有效地挖掘到时空大数据中隐含的信息,解决当前“数据过剩,信息匮乏”的困境[39]。本节主要从时空序列数据的角度出发,依次介绍了面向网格数据、面向图数据和面向轨迹数据的时空序列预测算法。
2.1 相关定义
在介绍相关算法之前,首先有必要给出时空序列和时空序列预测的定义。
时空序列:一系列具有空间关联的时间序列的集合。将目标空间χ划分为n个子区域,分别记为χ1,χ2,…,χn,第i个子区域χi内的变量在时刻j的观测值为x i,j(i∈{1,2,…,n},j∈{1,2,…,t}),t为观测 时 间,区 域χi对 应 的 时 间 序 列 可 表 示 为X i,1:t={x i,1,x i,2,…,x i,t},则时空序 列(Spatio⁃temporal se⁃quence,STS)可表示为

时空序列预测:依据历史的时空序列,对未来某一段时间内时空变量的值进行估计的过程。已知历史时空序列STS={X i,1:t|i∈{1,2,…,n}},预测观测时间t后L个时刻时空变量的值,即

式中E1:t为时刻1到t的其他特征。
2.2 面向网格数据的预测算法
2.2.1 网格数据建模
在时空序列预测问题中,可将目标空间χ划分为一个包含n个地点P×Q的网格图,其中n=P×Q,则在每一个时刻所有采样点可以视为一张图片P×Q×D上的像素值,其中P,Q,D依次为该图片的宽度、高度和通道数(该通道数D对应每个采样点取值的维度数)。因此,计算机视觉领域的各种算法可以由此迁移到时空序列预测问题中来提取n个地点间的空间关系。
例如,在北京出租车数据集(TaxiBJ)中,将同一时刻不同节点的人口流入量建模成一张32像素×32像素的图片(实际上应该为32像素×32像素,为了简化省略了最后一个维度),则2013年7月1日0:00~0:30的流入人流量对应图片用热力图可视化如图3所示。其中,图右侧的长条表示热力图颜色和人群流入数量的对应关系,热力图的纵横坐标(取值范围0~31)用于确定每个特定的节点区域。

图3 北京2017年7月1日前半小时流入人流量热力图Fig.3 Heatmap of inflow of people in the first half hour of July 1,2017 in Beijing
2.2.2 面向网格时空数据的深度预测算法
时空序列数据由时间序列拓展而来,现有的时间序列 预 测 方 法 如 循 环 神 经 网 络[40](Recurrent neural net⁃work,RNN)、长短期记忆网络[41](Long short⁃term mem⁃ory,LSTM)、门控循环单元网络[42](Gated recurrent unit,GRU)和 时 间 卷 积 网 络[43](Temporal convolutional net⁃work,TCN)等可以提取出数据中的时序特征,但是在将其应用到时空序列预测中时却往往忽略了时间序列之间的空间关联。Shi等[44]在2015年提出了Conv⁃LSTM模型来解决这个问题。ConvLSTM模型是卷积神经网络[45](Convolutional neural network,CNN)和循环神经网络LSTM的结合体,通过对全连接LSTM网络[46](Fully connected LSTM,FC⁃LSTM)进行拓展,将LSTM中的一维张量拓展为三维张量(对应的点乘拓展为卷积操作),因而能够捕获到数据中的时空特征,该模型当时在利用雷达回波数据进行降雨量预测的问题中取得了很好的效果。ConvLSTM模型的思想启发了将CNN结构引入时空序列预测中的一系列模型。
为了挖掘网格时空数据间的空间特征,可以将其建模为一系列图片序列,然后再用卷积神经网络、残差神经网络[47](ResNet)等来提取空间特征。Zhang等[48]2016年在Deep ST模型中首次将这个思路应用到了交通流量预测这个时空序列预测领域的代表性问题中。DeepST将每个时刻的交通流量建模成一张图片,利用不同的时间尺度(半小时、一天、一周)分别对数据采样得到3个序列,利用相同的CNN结构对这3个序列分别进行特征提取,之后对得到的这3个特征进行加权融合最后得到预测结果。2017年,Zhang等[49]对DeepST模型提出了改进,在其卷积的基础上增加了残差模块,最后融入外部特征构建了ST⁃ResNet模型。通过引入残差模块,ST⁃ResNet确保了预测精度不会因为卷积模块层数的增加而降低。
Deep ST和ST⁃ResNet虽然能提取到空间特征,但是对于时间特征的提取较为粗略。在此基础上,Li等[50]于2019年提出了ST⁃DCCNAL模型。该模型在将同一时刻不同位置的时空变量建模为图片的基础上引入了LSTM结构。针对空间特征的提取,该模型引入了DenseNet[51]来解决CNN在传播过程中存在信息损失的问题。ST⁃DCCNAL先利用DenseNet结构提取每个时刻的空间特征,再利用LSTM提取时间特征形成时空特征。考虑到不同时刻的历史数据对待预测值的影响大小不一样(时间间隔越近,影响越大),ST⁃DCCNAL模型还在LSTM中添加了注意力机制[52],自动学习到了不同时刻对应的不同权重。
实际应用中,空间距离相近的区域往往具有相似的时间模式变化规律,因此Yao等[53]提出了一个多视角的模型DMVST⁃Net来解决这个问题。该模型从空间视角、时间视角和语义视角来提取时空特征,其中空间和时间视角分别利用了局部CNN和LSTM来进行特征提取。语义视角则是通过构建一个加权图(节点之间边的权重代表不同区域之间功能的相似程度),然后将其映射编码到隐空间提取到语义特征,之后将语义特征和之前提取到的时空特征融合最后得到预测结果。
上述模型都有一个假设,那就是区域之间的空间关系是固定不变的。然而在实际中空间区域节点之间的空间关联往往会随着时间而变化,例如工作日和周末时商业区域和住宅区的人流量变化规律差异较大。为了捕获到这种动态的时空关联,Yao等[54]提出了STDN模型。在提取每个时刻的空间关联时,STDN利用当前时刻的人流移动方向矩阵和人流量矩阵点乘进行加权,从而刻画了每个时刻的空间关联。此外,该模型还利用了一个带有注意力机制的LSTM提取每天中蕴含的时间关联,再利用一个LSTM提取天与天之间的时间特征,从不同粒度挖掘出了数据的时空特征。
2.3 面向图数据的预测算法
尽管上述的时空序列预测算法较好地捕获了数据中动态的时空关联,但这些方法只适用于网格时空数据,即欧式空间的时空数据(如分别在一维、二维和三维欧几里得空间的文本、图片和视频等)。在实际生活中,大部分时空数据都是非欧几里得空间数据,例如知识图谱[55]、社交网络[56]、化合物分子结构[57]等。这些非欧数据往往无法建模成一系列图片,强行建模成图片序列会极大地降低预测的精度。因此面向图数据的时空序列预测算法逐渐成了研究的重点和难点。
2.3.1 图数据建模
在面向图数据时空序列预测问题中,将时空序列定义在图上。对于时刻t在节点i的变量观测向量X i,t并非是独立的,而是与图中其他每个节点都有一个成对的连接。因此观测向量X i,:可以视为节点i定义在图G(无向图或有向图)上的图信号。第t个时刻,图可表示为G t=(X:,t,ξ,W),其中X:,t是t时刻所有n个节点特征的集合,ξ是边的集合,表示了节点之间的连通性,W∈Rn×n是图Gt对应的加权邻接矩阵。
2.3.2 面向时空图数据的预测算法
最早将图卷积网络[58]应用于时空序列预测问题的是北京大学的于斌,他在2018年的IJCAI会议论文中提出了STGCN[59]算法。该算法将问题建模在图上,摈弃了RNN结构而全部用卷积结构来替代。该模型利用一个门控线性单元和一维卷积结构构建成一个时序门控卷积模块(Temporal gated⁃conv,TGC),然后将一个空间图卷积模块(Spatial graph⁃conv,SGC)夹在两个时序门控卷积模块之间形成一个基础的时空卷积单元。通过堆叠这些时空卷积单元,并在之间增加残差模块,STGCN有效地提取到了时空图数据中的中长期时空特性,并较好地减少了模型参数,增加了训练速度。
STGCN模型尽管因为未使用RNN结构而训练较为迅速,但其对时间特征的提取较为粗略。基于此,2019年Guo等[60]提出了ASTGCN模型,该算法在基础时空特征提取模块之中引入了注意力机制。在时间特征和空间特征提取时加入注意力机制使得该模型能够捕获动态而复杂点的时空关联。此外,ASTGCN模型还引入了类似于DeepST中的不同时间尺度(半小时、一天、一周)的子序列,分别堆叠基础时空特征提取模块后将特征融合后预测,使得模型提取的时间特征更加符合实际变化规律。
同样,针对道路网络拓扑结构的非欧性,Zhao等[61]提出了T⁃GCN模型。该模型和ST⁃DCCNAL模型类似,都是先对每个时刻的空间特征提取,再利用RNN结构捕获空间特征序列中蕴含的时间关联。不同的是,T⁃GCN使用了图卷积神经网络挖掘非欧数据中的空间特性,利用了参数更加精简的GRU替代了LSTM模块。最后在两个实际数据集上验证了T⁃GCN模型的有效性。
STGCN在空间特征提取时只利用了一个邻接矩阵,但实际中除了物理空间距离相近的区域有类似的时间变化模式之外,如果两个区域功能相似,或者两个区域之间有交通间接连接,那么这两个区域对应的时间序列应该也有相近的变化规律。为了解决这个问题,Geng等[62]提出了一个时空多图图卷积神经网络STMGCN。该模型从区域邻近性、功能相似性和连通性3个角度分别构建了一个图,然后在每个图中都引入了一个环境门控RNN来提取时间特征,再利用GCN提取特征并将3个图得到的时空特征进行融合得到预测结果。
在实际应用中,道路网络时空数据往往是非平稳的,并且缺乏环境信息,为了增强模型预测性能,Dai等[63]在2020年提出了HSTGCN。HSTGCN旨在预测两个地点之间的通行时间,为导航应用提供后台算法支撑。为了解决环境信息匮乏的问题,该模型除了利用历史的通行时间时空序列之外,还引入了和通行时间强相关的交通流量数据。利用一个Transformer结构对交通流量数据进行特征提取,然后与通行时间数据分别送入一个时序门控卷积模块中提取其时间特征并融合。之后再将得到的特征送入GCN网络中之后再利用时序门控卷积模块提取时间特征最后得到预测结果。HSTGCN可以看作是只有一个基础时空卷积单元的STGCN模型,不同的是HSTGCN增加了交通流量数据来辅助进行预测,此外还对原有的邻接矩阵进行了重定义使得交通固有的邻近性得到了更好的表示。
尽管和面向网格时空数据的深度预测算法处理的数据类型不同,这两类算法在某些方面有共同的特点。这两者的一些特征提取模块可以相互借鉴迁移,一些相应的技巧也是通用的。
2.4 面向轨迹数据的预测算法
行人轨迹预测广泛应用于自动驾驶[64]和机器人导航[28]等领域。准确地预测行人的轨迹使得自动驾驶的车辆、机器人等能及时地避开障碍,对于它们的安全行驶具有重大意义。在传统的轨迹预测方法中,有的利用贝叶斯推断来研究周边环境进而预测行人移动意图[65];有的从人的角度出发,利用社会力模型构建Social Force[66]模型,通过研究人的社会属性来预测行人的轨迹。本节主要介绍基于深度学习的时空轨迹预测算法。
2.4.1 轨迹数据建模
轨迹预测是依据预测对象历史的轨迹位置预测未来一段时间内位置的过程。对于场景中的每一个研究对象i(i∈{1,2,…,n}),其在时刻t所处的位置可用坐标pi,t=(x i,t,y i,t)表示。给定研究对象历史的位置序列pi,t(t∈{1,2,…,T}),预测未来L个时刻他们的位置p i,T+1:T+L,未来第k个时刻的位置可表示 为
2.4.2 面向时空轨迹数据的深度预测算法
轨迹预测可以视为一个序列生成任务,经典的时间序列处理算法如RNN、LSTM等可以被用在轨迹预测之中。将每个行人的轨迹视为一条独立的时间序列,虽然可以提取到各自的时间特征,但彼此之间的空间关联却被忽略了。为了解决这个问题,Alahi等[67]于2016年提出了Social⁃LSTM模型。该模型将每个行人视为一条时间序列,用LSTM结构来提取各自的时间特征。同时Social⁃LSTM引入了一个“Social”池层共享LSTM的隐藏状态来模拟行人之间的交互。通过将特定半径内所有LSTM的隐藏状态汇集在一起作为下一时间步的输入,该模型能自动学习在时间上一致的轨迹之间发生的交互。
尽管Social⁃LSTM能够依据邻近性来刻画行人间的交互,但这并不完全符合实际情况。实际上不同距离不同方向的行人对自动驾驶的汽车(或机器人)的影响大小也不一样。因而Vemula等[68]提出了Social Attention模型,该模型利用注意力机制来捕获不同人的相对重要程度,根据神经网络的隐藏状态所代表的运动模式来分配不同的权重。与基于池化机制的模型相比,基于注意力的模型能获得更丰富的交互信息,实现更准确的预测。
行人轨迹不仅受行人本身影响,还会和周围的目标进行交互。之前的方法都是利用各种集结方法将学习到的不同行人状态融合在一起,Social⁃STGCNN[69]则通过构建图的方式替代了这个集结方法。通过GCN提取到一个时空的隐状态,然后送入到一个时间外推卷积神经网络中得到预测结果。实验表明,Social⁃STGCNN模型不仅提高了预测精度,还有效地提高了数据利用率,仅用五分之一的数据就超越了之前的最好结果。
为了更充分地利用行人交互信息,周于涛等[70]提出了一个基于LSTM和GCN的模型,该模型利用图卷积网络中的节点表示行人的运动信息,节点之间的边表示行人之间的交互并且利用了自注意力机制来计算行人间的交互程度。此外该模型还捕获了行人间的伴随行为特征,并在损失函数中体现了这一点,实验表明该模型相比于之前方法预测性能有了较大的提升。
为了进一步对各种时空序列预测算法的特征提取进行对比,表2列出了各类预测算法中一些代表性算法的特征提取比较。
本文提及的基于深度学习的各种预测方法总结如表3所示。

表2 部分时空序列预测算法特征提取对比Table 2 Feature extr action and comparison of par tial spatio‑temporal sequence pr ediction algor ithms
3 下一步研究方向
基于深度学习的时空序列预测方法虽然在不断发展,但目前仍然存在许多问题。针对一个应用领域的时空序列预测方法如何迁移到别的应用领域中,目前也缺乏一个统一的框架来对不同领域的各种预测算法进行性能评估比较;建模时往往默认为数据的分布不会随着时间变化,但实际上时空变量受到环境的影响,当环境变化时时空序列数据的分布也有可能发生漂移,因此需要建立一个自适应的时空序列处理框架来应对变化更加复杂的时空数据。此外,基于深度学习的模型严重依赖于大量数据去训练,对于某些关键数据匮乏的区域则力有未逮,因而需要探索新的方式来解决数据匮乏问题;在实际应用中,某些领域对于模型的规模和实时性要求较高,如何简化模型,提高预测的时间效率也是研究的重点。综上所述,基于深度学习的时空序列预测算法还可以沿下面的方向进一步研究:
(1)建立统一框架。可以从数据特征出发,建立一个统一的框架,例如将模型分为时间特征提取、空间特征提取、环境特征提取3大部分,具体提取的方式又可以往下细分。这样不仅可以将时空序列预测模型迁移到不同的应用领域,也方便下一步对各个模型进行评估比较。此外,一个统一的预测框架还能够指导创建新的模型,对时空序列预测领域有着极大的意义和价值。
(2)解决数据分布漂移问题。从数据分布的视角出发,已有的预测方法都是建立在数据独立同分布的假设之上,这也是当前阻碍模型预测精度提高的瓶颈之一。针对时空序列数据的分布随时间变化的实际情况,可以考虑利用自适应学习的方式来解决数据分布漂移问题。
(3)解决数据匮乏问题。针对关键数据匮乏问题,一是考虑利用迁移学习的方式,将数据充足且有相似点的区域学到的模型迁移到数据匮乏的区域;二是进行数据增广,将研究数据进行重采样等变换,也可将与研究对象相关的其他数据引入进来辅助进行预测。
(4)模型压缩和实时性。为了满足模型能在轻量化的设备上使用的要求,需要对模型进行剪枝压缩,在保证一定精度的情况下对模型做出简化。对于某些对实时性要求较高的应用场景,可以考虑将在线学习融入到时空序列预测之中,进而使模型能够及时更新和响应预测。

表3 基于深度学习的时空序列预测方法总结Table 3 Summary of spatio‑temporal sequence prediction methods based on deep learning
4 结束语
本文首先阐述了时空序列的背景,简要介绍了传统的时空序列预测方法,随后对时空序列的数据特点和实际应用做了详尽的描述,然后介绍了在网格数据、图数据和轨迹数据这3类主要的时空数据中如何利用深度学习来进行预测。时空序列预测在现实生活的各领域都起着重要作用,如何利用深度学习进一步挖掘出时空数据中的隐含特征,提高预测的精度是研究者们需要努力的方向。

