柴油机缸套变形对配缸间隙特性的影响
田新伟,赵忠诚,褚国良,江雨晨,胡勇,刘营
1.内燃机可靠性国家重点实验室,山东 潍坊 261061;2.潍柴动力股份有限公司,山东 潍坊 261061;3.山东大学 能源与动力工程学院,山东 济南 250061;4.山推工程机械股份有限公司,山东 济宁 272073
0 引言
随着国家排放标准日趋严格[1-2]和对油耗的限制,柴油机的研究逐渐向高功率、轻量化方向发展[3-4]。柴油机高强化的发展趋势导致燃烧室内最大爆发压力提高、单位时间内放热量增加[5-6]、缸套承受的机械载荷和热负荷增大,柴油机相关组件的设计面临严峻考验[7]。
为保证活塞在气缸内的往复运动,二者之间存在设计配缸间隙[8-9],配套间隙导致运动过程中活塞轴心相对初始轴心倾斜偏移。由于活塞与缸套物性不同造成变形差异,活塞与缸套之间的最小配合间隙与初始设计配缸间隙相比产生较大波动[10-12]。缸套为圆筒形薄壁结构,在高温高压下极易产生变形。Franz等[13]通过试验和仿真相结合的方法对缸套变形进行研究,为缸套变形分析提供了完整思路;文献[14-15]通过傅里叶分解对缸套变形进行研究。本文中围绕缸套变形与配缸间隙展开研究,通过改变单一阶次的缸套变形并进行叠加,分析不同阶次缸套变形对配缸间隙的影响,为缸套的设计提供参考。
1 活塞变形轮廓
为获得工作状态下配缸间隙,在假定活塞与缸套均为圆筒形结构的基础上,减去二者变形量,并利用仿真计算软件分别对其进行应力分析。通过建立活塞组件的耦合模型,计算得到活塞承受热负荷与机械载荷共同作用时的位移分布,如图1所示(图中单位为μm)。由图1可知最大位移约为102.5 μm。从位移场中提取各节点变形后坐标,利用最小二乘法拟合变形后活塞中心轴线坐标,相对初始轴心偏移1.36~27.92 μm,与总体位移之比为0.273。由于缸套的圆心偏心对整体位移有较大影响,将偏心剔除后的位移转换坐标系,获得符合AVL Excite多体动力学仿真软件要求的活塞变形轮廓型线,如图2所示。
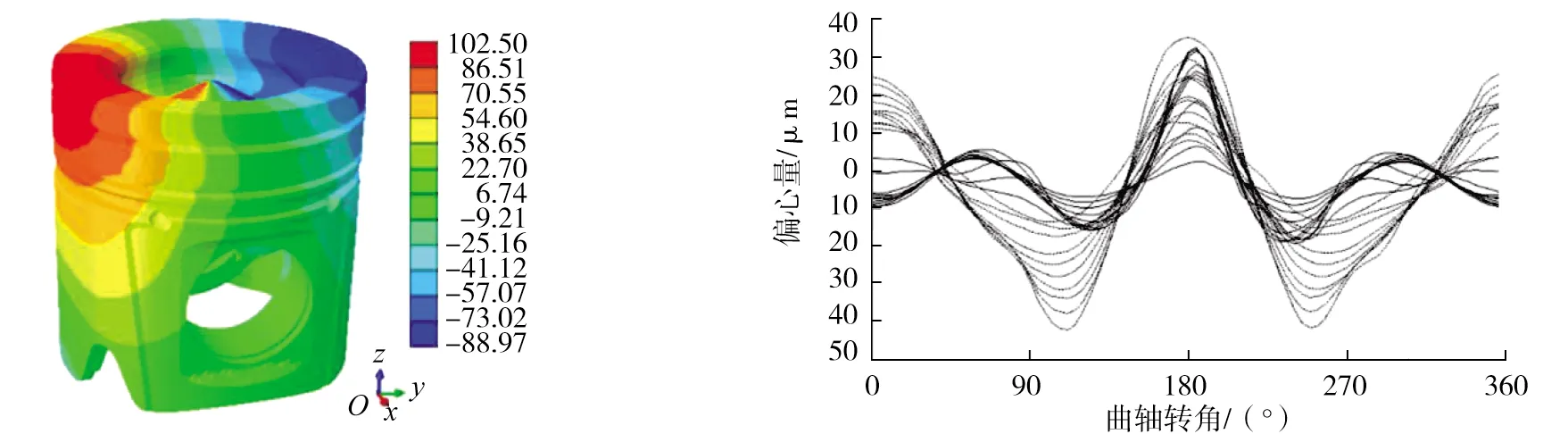
图1 活塞位移分布 图2 活塞变形轮廓
2 缸套变形轮廓
搭建缸套组件的耦合模型,求取缸套在同时承受预紧力、热负荷以及机械载荷时的位移分布,如图3所示(图中单位为μm)。由图3可知,缸套最大位移约为447.8 μm。

图3 缸套位移分布
对缸套变形进行傅里叶变换,一个完整波形可以通过不同频率波形叠加获得。若采用极坐标系表示缸套变形,缸套在同一水平高度上的周向节点变形可以视为随着极角变化的连续波形,并可以离散成不同频率的形变,即将缸套整体变形视为不同阶次变形的叠加。
傅里叶变换的数学表达式为:
(1)
式中:Δγ(θ)为缸套径向位移,mm;θ为极坐标系下的极角,°;Ai、Bi分别为第i阶时的傅里叶系数。
第i阶幅值即第i阶的最大缸套变形
(2)
缸套最大变形对应位置即极角
(3)
因此,柴油机缸套变形的傅里叶变换表达式为:
(4)
不同阶次变形在几何变化上的表现不同,第i阶的几何型线即为有个“叶”的变形分布,缸套1阶变形为整体的径向位移即变形后轴心相对于初始轴心偏移,0、2、4阶变形均以圆心为中心对称,各阶次几何意义如图4所示。

图4 缸套变形傅里叶变换各阶次几何意义
为获得变形后缸套的变形轮廓圆心,将缸套内壁面上的所有节点全部投影在气缸的横截面上,由最小二乘法拟合出中心点,代表轮廓圆心。无负荷作用下缸套圆心坐标与拟合后的变形轮廓圆心坐标求差值,可知偏心量约为2.4~107.3 μm,与最大位移之比为0.24,从而获得缸套1阶变形,通过傅里叶变换和逆变换去掉1阶偏心,获得更为准确的缸套变形,缸套的变形轮廓型线如图5所示。
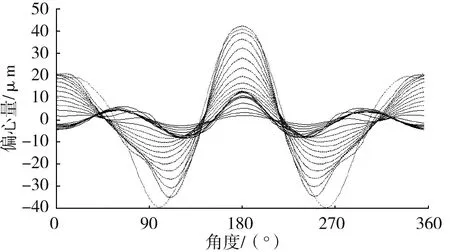
图5 缸套变形轮廓
3 缸套各阶次变形分析
在对缸套变形进行傅里叶变换分析时,通常认为缸套变形保留的主要阶数与缸套周围螺栓数保持一致。本文中在单一缸套周围存在6个预紧螺栓,所以研究缸套的前6阶变形。
缸套的0阶变形可以通过改变活塞环的膨胀和设计配缸间隙等进行补偿,因为0阶变形对应变形造成的直径膨胀,本质上相当于改变了活塞与缸套间的配缸间隙;缸套1阶变形对应缸套的整体偏心,影响缸套整体偏心的因素很多,如活塞销偏置、活塞自身的变形等。本文中主要研究在预紧力、热负荷以及机械载荷作用下的缸套变形,从缸套2阶变形开始研究。
定义缸套底部截面的高度为0,从缸套底部至顶部为缸套中心轴线y的正方向,缸套顶部对应的截面高度为223 mm,中部对应的截面高度为110 mm,对底部、中部和顶部3个高度的变形分别进行傅里叶变换,得到不同水平截面上缸套变形各阶次幅值,如图6所示。由图6可知,随着傅里叶阶数增大,各截面高度处的缸套变形均减小,说明阶次越高,变形越小;缸套底部截面处各阶次变形幅值最小,中部次之,顶部截面处变形幅值最大。
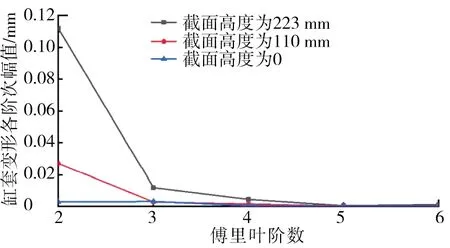
图6 不同截面高度缸套各阶次傅里叶变形幅值
4 缸套各阶次变形对工作配缸间隙的影响
由于缸套变形可视为由幅值和相位不同阶次变形叠加形成,在进行傅里叶逆变换之前,首先对单一阶次的缸套变形进行幅值增减,计算工作配缸间隙特性时,仅改变某1阶次变形,其他阶次幅值不变。柴油机的工作配缸间隙特性包括工作状态下的最小配缸间隙、活塞裙部润滑特性和缸套振动特性,活塞裙部润滑特性包括活塞裙部与缸套间的最小油膜厚度、活塞裙部与缸套间最大油膜压力以及活塞裙部与缸套间的摩擦功耗,而缸套振动特性通过缸套外壁面测点的最大振动加速度反映。在缸套外壁面主推力侧(thrust side,TS)和次推力侧(anti-thrust side,ATS)各提取5个不同截面高度位置上的节点作为振动测点,具体位置分布如图7所示。

图7 缸套外壁面振动测量点
以2阶缸套变形为例进行分析。提取缸套的2阶变形,分别将其缩小50%和放大至150%,通过傅里叶逆变换获得缸套总变形,并与实际变形的最小配缸间隙及其工作特性进行对比,为保证仿真结果的准确性和稳定性,提取虚拟样机模型第2个完整循环的结果即曲柄转角为720°~1440°时的运行结果进行分析,各特性变化曲线如图8所示。

图8 2阶变形幅值对工作配缸间隙特性影响
由图8可知:改变2阶变形幅值后,最小配缸间隙总体变化趋势保持一致;2阶变形越大,最小配缸间隙越小,这是因为2阶变形对应缸套椭圆度的变化,当2阶变形增加即缸套椭圆度增加时,沿垂直活塞销孔轴线方向,活塞与缸套间的直径之差增大,活塞换向时的倾斜角度增大,活塞与缸套间的拍击力增加,导致活塞与缸套间的最小油膜厚度减小,最大油膜压力减小,最大摩擦功耗增加,使得活塞与缸套间的润滑特性变差;同时当缸套2阶变形增加时,活塞与缸套间的间隙更大,发动机运转过程中活塞轴心偏转程度增加,与缸套轴心的同轴度相对降低,使得缸套外壁面最大振动加速度增大,振动特性变差。
将极差定义为3组方案中最大值与最小值之差。将极差与平均值的比定义为波动度,由于不同性能指标的数量级存在差异,波动度可以更好地表征各方案结果偏离平均值的变化范围,从而反映各参数与结果的关联程度。2阶变形不同幅值对应的3组方案结果如表1所示。

表1 2阶变形幅值变化对应结果
由表1可知:2阶变形幅值对最大摩擦功耗的影响最大,波动度为31.42%;其次是最大振动加速度,波动度为24.68%,影响较大;最大油膜压力波动度为8.97%,存在一定影响;而最小工作配缸间隙和最小油膜厚度的波动度较为接近,约为1.5%,作用不明显。
按照上述分析流程,对缸套3~6阶变形缩小及放大后进行傅里叶逆变换获得总变形,并与实际变形形成3组单一变量对照方案进行仿真分析,对应最小工作配缸间隙及其工作特性如表2~5所示。

表2 3阶变形幅值变化对应结果

表3 4阶变形幅值变化对应结果

表4 5阶变形幅值变化对应结果

表5 6阶变形幅值变化对应结果
由表2可知:3阶变形幅值相对2阶整体下降,其中最大振动加速度的波动度仍然较大,为17.11%,最大油膜压力的波动度相对2阶略有增加,为10.96%;最大摩擦功耗波动度大幅降低,只有7.83%;最小配缸间隙和最小油膜厚度的波动度基本不变,约为1.5%。
由表3可知:4阶变形幅值波动度整体下降,最小配缸间隙和最小油膜厚度的波动度大幅下降,为0.19%;最大油膜压力和最大摩擦功耗的波动度分别下降为8.16%和3.62%,最大振动加速度的波动度大幅下降为1.54%。由表4、5可知:5、6阶变形波动度均小于4%;5阶变形的最小配缸间隙和最小油膜厚度的波动度为0.23%;6阶变形时,最小配缸间隙和最小油膜厚度的波动度为0.09%,可以忽略。
此外,对比分析不同阶次变形可知,3~6阶变形对波动度影响呈现不同幅度的减小,3阶及3阶以上阶次的变形幅值波动度大幅降低。相对2阶变形,3~6阶变形对最小配缸间隙和最小油膜厚度的影响均很小,尤其是4~6阶各参数的波动度都可忽略不计。阶次越高,变形幅值波动度越小;同一特性下,2阶变形的波动度是6阶变形的9倍以上。
5 结论
1)缸套变形各阶次幅值波动对工作配缸间隙特性的影响不同,对摩擦功耗峰值和最大振动加速度幅值影响较大,对最大油膜压力的影响次之,对最小油膜厚度和最小配缸间隙的影响极小。
2)缸套变形阶次越高,变形幅值波动度越低,2阶变形波动度最大,6阶最小;同一特性下,2阶变形的波动度是6阶变形的9倍以上,在对工作配缸间隙进行优化设计时应着重考虑缸套2阶变形。

