V形硅纳米球团簇的多极散射分析

何颖君，杨俊桦，陈丽芳，陈星源，徐祥福，赖国霞

（广东石油化工学院，广东茂名 525000）

近年来，在纳米尺度上对光波进行操控的技术受到了光学和光子学界的广泛关注［1-3］.对于金属材料的纳米结构，强烈的光与物质相互作用可以通过光波与金属中自由电子振荡的耦合来实现.这种所谓等离激元的激发现象可以在孤立的单体或者有目的设计成的阵列形式结构中进行，即超材料或超表面.然而，等离激元的激发天然伴随着欧姆损耗，进而导致光波能量的损耗，给潜在应用造成阻碍.最近，高折射率电介质纳米粒子作为功能性光操纵器件的重要组成部分引起了研究人员的注意［4-6］.例如，研究者已经使用纳米硅球排列成的一维链式结构实现了工作在可见光波段的全电介质Yagi-Uda型天线［2］.电介质粒子对光的散射机理与金属粒子有很大的不同.对于等离激元，光的耦合或控制是通过自由电子的振荡实现的，而对于电介质材料，散射过程包含有一系列多极子辐射的贡献［7-10］，这些多极子的成分与粒子的形状、大小以及材料的介电常数、光波长等有复杂的关系.因此电介质粒子的散射可以提供更多的自由度，例如在金属中不容易实现的磁偶极子［11］或者环形偶极子［12］可以在米共振中观察到.事实上，通过对激发的多极子之间的干涉进行仔细的设计，研究人员已经获得了一些特异的散射行为，如横向的Kerker散射［13-14］以及无辐射的Anapole［15-16］.

虽然高折射率电介质粒子的无损特性使其在模拟和替代等离激元结构的作用方面有很大的潜力，但其功能设计非常复杂.这是因为对于特定的任务，由于微纳尺度上粒子之间的距离甚短，需要考虑到粒子间的相互作用效应，以便在每个粒子中选择性地激发多极子作为辐射源.到目前为止，只有对于相对简单的结构，例如光学纳米二聚体［17］或者核壳结构［18］像耦合多极子模型这样的分析工具才被用于辅助设计分析，但是这种模型的复杂性随着粒子数量的增加而迅速增加.而对于实际功能器件，如超表面，则需要从粒子数更大的单元结构中获得额外的设计自由度.在这种情况下，我们拟通过本文中研究一个由五个纳米硅球组成的V形小团簇的散射特性.具体地，我们将证实在这样的结构中也可以实现类似于二聚体散射的定向性，而主要散射参数随激发波长的光谱分布则可以通过多极子辐射贡献来分析.本文介绍了散射多极方法的主要理论，给出主要的计算结果，并通过多极子辐射系数对计算结果背后的物理机制进行分析.

1 散射的多极子辐射理论

本文研究的纳米粒子团簇如图1所示.在x-z平面上，五个相同且半径为70 nm的硅球被排列成一个V形团簇，置于真空中.V字的两臂上各球之间的距离均为70 nm，两臂之间的夹角为2θ=75°.入射光波为沿z轴正向传播的x方向偏振的平面波.根据米氏散射理论，球坐标系中的散射场Es可以分解为由无穷多项多极子构成的级数［8，19］：

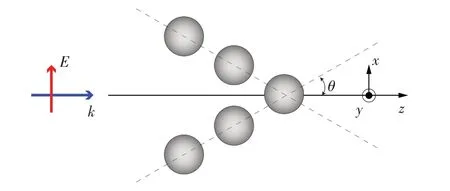
图1 纳米硅球团簇的位置结构和入射光方向示意图Fig.1 Schematics of the structure and position of the silicon nano-sphere cluster and the direction of incident light

磁多极项可以达到与电多极项同等量级的程度.对于我们使用的硅材料，其相对阶电常数为εr=12，因此可以估算，对于2R=140 nm的硅球，在可见光频率区内会出现较强的磁共振.

虽然式（1）可以看作是散射场的表达式，但实际上该式中的两类系数aE和aM的确定需要结合问题的边界条件加以确定.对于本文研究的问题，虽然粒子数量较小，但由于粒子的分布造成了复杂的边界条件，所以通常使用解析手段得到aE和aM是非常困难的.但由于该式中其余函数都为已知，所以公式实际用途首先是使用某种数值方法求解出散射光场Es在整个空间的分布，然后利用得到的散射场代入公式来求解出各项多极子的系数从而分析各种多极子在散射场中的贡献.利用矢量球谐函数Xlm和标量球谐函数Ylm的正交性，多极子的系数有如下的表示式［19］：

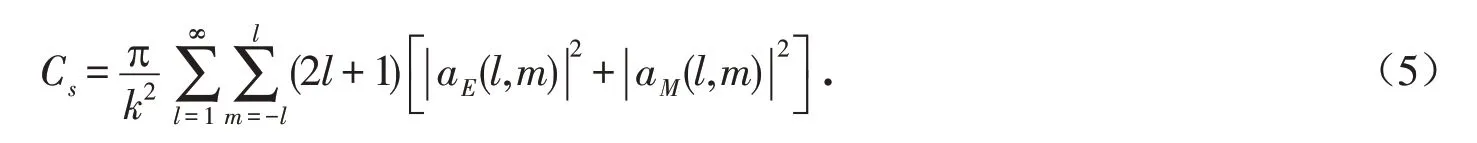
本研究关注的另一个散射特性的指标是所谓散射的方向性D，它的量化定义为［4］

其中：p(θ,ϕ)是作为方向角(θ,ϕ)函数的散射功率；P是在所有方向的总功率；max[∙]表示取最大值，即方向性定义为散射功率中的最大值与散射功率的方向平均值之比.

2 V形硅纳米粒子团簇的散射特性

图2 各类多极子对散射截面的贡献Fig.2 Contributions from various multipoles to the scattering cross-section

对500～1000 nm波长范围内的入射光场的散射进行了数值计算，进而利用公式计算了对散射场贡献的电、磁偶极子和电、磁四极子的系数.将得到的多极子系数代入公式，就可得到不同多极子成分对散射截面的贡献，如图2所示.从图中可以看出，多粒子团簇的散射特性与单粒子的散射有几方面明显的不同，首先，电偶极子辐射强度随波长的分布出现了多个峰值，而单粒子一般表现为单峰，这是由于粒子之间通过散射光相互作用导致的所谓间隙模式所导致；另外，电四极子的强度有显著的增强.根据单粒子的米散射理论［21］，对本研究所使用的远小于波长的粒子尺寸，电四极子的贡献应该远小于偶极子成分.

但是对于本研究的团簇情况，电四极子在波长λ≈570 nm附近出现强烈的峰值，其贡献超出电、磁偶极的贡献.这是多粒子相互作用中干涉增强的结果.同时可以看出，与其他三个多极子相比，磁四极子的贡献很小.在波长λ≈600 nm的位置，电、磁偶极子与电四极子重叠，这可能导致在600 nm附近的辐射具有高方向性.

图3给出了从λ=500 nm到λ=1000 nm区间中6个波长位置的散射功率方向分布图方向图中的0°为x方向.从x-z平面内的方向分布可以看出，在λ≈600 nm附件，确实出现了显著的前向散射.而从x-y平面中的方向分布，可以区分散射的主要来源.因为四极子辐射的显著特征是它的四个旁瓣，所以从图中不难看出，高方向性由电、磁偶极子贡献.而在波长λ=500 nm处，由于电四极子有一个次峰，所以显示出较为明显的四旁瓣.当波长接近于1μm时，由于四种多极子的激发都很弱，所以总的散射强度明显降低.

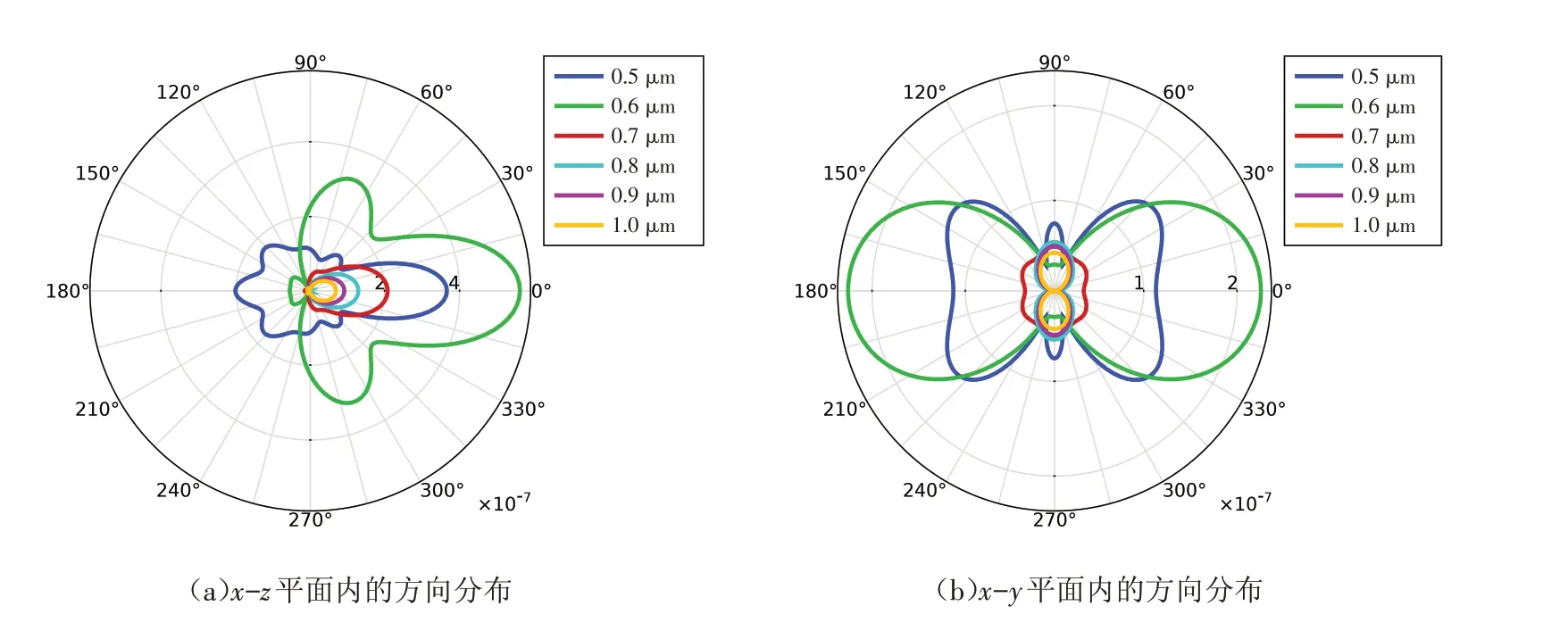
图3 散射远场功率的方向分布图Fig.3 Directional distribution of scattered power in the far-field

我们观察到另一个有趣的现象，在单个球体中是看不到的.从图2可以看出，磁偶极子的峰值几乎与电偶极子的右峰重合，这与单粒子情况有很大的不同，单球的磁偶极子通常位于较长的波长.由于两者峰值接近重合，因此它们之间的干涉有可能带来某个方向的散射增强.这种效应可以通过图4中给出的电偶极子和磁偶极子系数随波长的分布加以证实.两个系数在λ≈600 nm处绝对值都比较大，且符号相同.这就导致在该波长附近散射场的相长干涉.这一现象也通过图5给出的方向性参数D随波长的变化得到验证.结合图2与图5分析不难发现，图5中方向性的两个峰值中，靠近λ=500 nm的左峰，由于此处磁多极的激发远离共振波长，所以主要由电偶极辐射和电四极辐射贡献，而靠近λ=600 nm的右峰主要则主要来自电、磁偶极辐射.

图4 电偶极子与磁偶极子系数随波长的分布Fig.4 Distribution of the electric and magnetic dipole coefficients with wavelength

图5 方向性随波长的分布Fig.5 Distribution of directivity with wavelength

3 讨论与总结

我们研究了V形亚波长硅球团簇在可见光范围内的散射行为.研究表明，即便如纳米球的简单排列这样的结构也可导致有趣的散射行为和光谱特性.研究实现了小簇纳米球在平面入射波作用下的定向散射特性的同时，还发现团簇中粒子之间的相互作用会导致电偶极和电四极辐射的特异光谱分布，这些连同磁偶极分布形成的干涉对远场的散射角分布有主导性影响.研究还证明，使用多极辐射理论与数值计算相结合的方法，不仅可以得到有效的计算结构，还能对复杂体系散射特性的物理机制给予明确解释.本研究的结果连同研究方法，对使用较复杂纳米结构进行光调控的应用领域等有潜在应用价值.

本研究的结果中也揭示出一些物理上十分有趣和有潜在价值但不属于本文研究范畴的现象.例如，当纳米粒子数量从单个变成多个后，电四极子的贡献显著上升.然而根据经典的米散射理论，对于远小于波长的球形粒子，四极子的贡献很小.所以四极子增强现象背后的物理机制值得深入探索.由于篇幅关系，我们没有讨论当球形粒子之间的距离发生变化，或者V字的张角发生变化时，散射的光谱分布特性会受到怎样的影响.同理，当适当减少或增加粒子数量或者变化团簇形状时，散射机制可能变得更加复杂.也就是说，对于这样一个简单结构，其中可以自由变化的参数很多，这为针对特定目标对团簇结构进行优化设计提供了空间.

最后，本文所讨论的这种呈规则形状排列的团簇的生成方法属于跟本研究相配套的技术问题.但是随着当前纳米制备领域物理和化学合成手段的不断发展，有目的、精确地生成所追求的团簇结构成本和难度都在大大降低，因此本研究的实用性具有充分的技术保证.