桥梁混凝土中钢筋保护层厚度检测准确性分析

赵炯

（甘肃省陇南市文县交通运输局，甘肃 陇南 746400）

0 引言

混凝土混合钢筋材料可以为构造物提供稳定的支撑。但是二者的力学性质却存在巨大的差异。之所以可以混合在一起应用到构造物建造上，主要是因为混凝土材料和钢筋材料之间具有较强的黏合力，也可在荷载力的作用下一起变形，以此来实现结构功能的发挥。另外，二者的温度线膨胀系数相对较为接近：混凝土的膨胀系数范围为1.0×10-5～1.5×10-5oC；钢筋的膨胀系数则为1.2×10-5oC 在环境温度变化过程中，二者之间的黏结性不会受到温度应力的影响和破坏，且混凝土包裹在钢筋材料的外部结构上，不仅可以起到钢筋防腐蚀的重要作用，也可实现两种材料共同作用。由此可以明确的是，除了原材料能够影响钢筋混凝土的承载能力和耐久性之外，混凝土保护层的厚度也决定其各项性能的发挥效果。

1 钢筋混凝土保护层厚度的重要性

一般混凝土保护层都会被设计在钢筋构件的外缘表面上，以此来保护钢筋不受环境因素的侵蚀或者一些外界因素的破坏，也可提升钢筋与混凝土之间的黏结程度。

从承载力角度分析，保护层可以保障钢筋和混凝土二者同时受力。此时将保护层厚度设为c，钢筋直径设为d，根据相关受力分析结果可知，保护层厚度过薄，导致c 和d 的比值偏低。相关试验表明，该比值如果过小，很容易导致钢筋在受力变形期间，周边的混凝土受到钢筋变形所产生的环向拉力。在纵向方向上，保护层发生劈裂，降低二者之间的黏结强度。如果保护层厚度较大，那么可以根据其正截面受弯承载力的计算来表示其稳定程度。此时如果c 值偏大，那么截面的有效高度h0会小于设计数值，说明该建筑承载力不满足要求，对建筑设计的安全性造成负面影响。

从耐久力角度分析。混凝土自身属于高碱性环境材料，对钢筋进行包裹会形成一层保护膜，保护钢筋材料[1]。如果混凝土保护膜的厚度不足，会导致结构缺少足够的致密性。外界环境中的水分和气体等微量分子就会进入结构内部，腐蚀钢筋，甚至会导致结构膨胀，最终使整个结构失去支撑作用。另外，保护层过厚可以延长钢筋的使用寿命。

2 分布钢筋间距影响分析

2.1 试验构件

研究分布钢筋间距对箍筋保护层厚度检测精度的影响，设定采用两个厚度分别为30mm 以及35mm，钢筋分布及保护层厚度一致的构件进行试验。技术人员将各构件箍筋直径以及间距分别设定为12mm 以及15cm，分布钢筋直径设定为10mm，间距设定以10mm 为间隔，从70mm 至150mm。

2.2 试验结果

利用游标卡尺分别对试验所用的测试构件箍筋保护层厚度值进行一次试验检测，检测所得数据分别是30.06mm、34.62mm。之后使用软件对构件箍筋保护层进行了测量，将两次检测所得数据横向对比，最终获得数据对比结果。进行数据对比后总结：第二层钢筋（箍筋）保护层厚度与第一层分布钢筋的间距之间呈现负相关的关系，如若分布钢筋的间距越小，那么箍筋的保护层厚度就会越大，反之则越小[2]。

经过详细检测，最终获得两个测试构件箍筋保护层厚度分别为30.06mm 以及34.62mm。在得到相应数值后利用专业的Profometer5 对试验所用构件箍筋保护层厚度进行测量，并将软件测量结果与实际测量结果进行对比分析，形成厚度对比结果。如若第一层钢筋间距达到相应数值后，第二层箍筋保护层厚度就不会受到第一层钢筋的影响。如若第一层分布钢筋的间距超过1.3cm，那么经过Profometer5 测量所得的数据都会保持29mm 和34mm。

3 率定曲线

3.1 率定试验

在进行检测过程中，选取一段与检测构件材料相同，长度为500cm 的钢筋。在测试过程中，首先确保探头设备以及钢筋之间保持平行状态，随后依照一定频率控制探头向钢筋方向靠拢，最终测定探头底面与钢筋表面之间的距离，为后续研究提供真实数据支持。完成测量工作后，分别将仪表读数以及测定模拟保护层厚度设定为纵坐标和横坐标，绘制出相应的率定曲线。

在完成此步骤后，依照相关文件规定的桥梁施工要求，对钢筋和箍筋的布设方案进行设计。此工程使用与25mT 梁相同的钢筋材料开展试验。此次试验中设定箍筋以及分布钢筋直径分别为12mm 以及10mm，间距分布控制在12cm 以及90mm、100mm、110mm、120mm。在实际工作中利用不同厚度均值垫块作为保护层开展试验，其厚度控制在25～55mm 区间范围内。

在对垫块保护层的厚度进行检测，随后利用钢筋位置测定仪对模拟的保护层厚度进行测定，并且记录数据，所获得数据用H 表示[3]，不同保护层厚度、不同分布钢筋间距下箍筋的测试结果见表1。

3.2 率定曲线及率定公式

在实际工作中将仪表读数H 以及实际保护层厚度值分别设定为纵坐标和横坐标，并在充分依据如表1中所示测定结果前提下，对各分布钢筋间距率定曲线进行绘制，得出箍筋保护层厚度率定曲线[4]。

表1 率定试验结果

为确保工程应用便捷性，可以使用保护层修正计算公式对不同公式条件下获取的计算结果进行整理，所获得数据带入率定曲线公式中拟合，最终获得误差率，形成率定公式见表2。表2中，Hx以及H分别表示保护层厚度修正值以及仪器显示值，进而可得误差率计算公式为（Hx-实际值）/实际值×100%[5]。由表2中数据可知，各率定公式计算结果以及实测值之间误差率较小，最大值为1.4%。

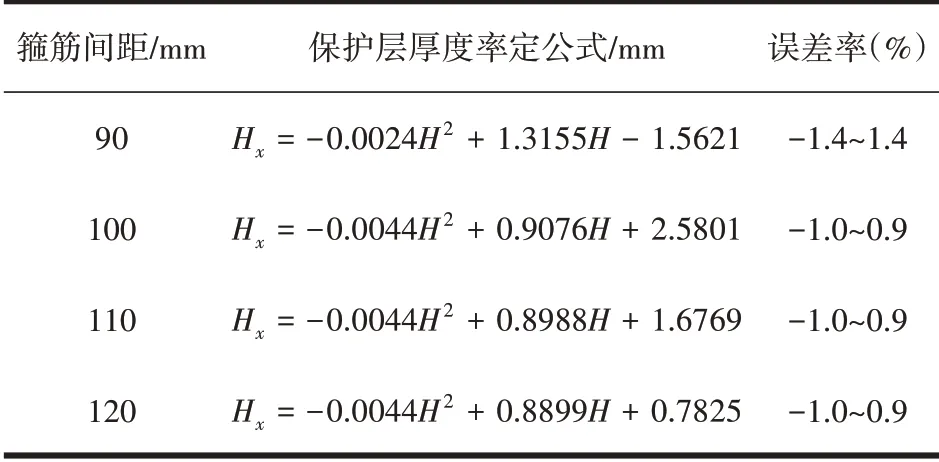
表2 率定公式以及误差率

4 实例验证

为验证修正公式实用性，选取某地区桥梁工程进行实践验证。案例工程为某地区依照交通运输部发布的标准图纸设计建造的25mT 梁桥。试验研究过程中将目标桥梁的跨中截面箍筋保护层厚度设定为36mm，同时设定钢筋依照10mm 间隔分布布置。随后借助专业的钢筋位置测定仪，开始测定钢筋保护层厚度（H），同时利用测定仪对已经测定的钢筋段相邻的两个钢筋分布位置进行标定，测定钢筋分布间距，所得数据为L。最后利用计算公式获得钢筋修正值，即Hx。在进行验证时，选择在现场凿孔对保护层厚度H3进行检验。在检验中共计测了7 根箍筋，最终所获得的所有数据详见表3。

表3 T 梁保护层厚度分析表

依据表3中数据可知，率定公式修正值以及凿孔实测值基本保持一致，最大误差以及最大误差率分别为1.19mm 以及4.1%，由此可见，率定公式计算结果精准度满足实际需求，可以用于工程实践之中。

将表2以及表3进行横向对比可知，表3中的误差率均明显高于表2中的误差率。经过研究发现，导致这一现象的主要原因是率定修正公式拟合的依据为室内试验推导，与试验过程中应用的保护层和实际施工现场混凝土检验之间存在的差异较大。因此，为了能够最大程度提升率定修正工作的精准度，在对率定公式进行更深层次的研究中，应选用与现场测试构件以及钢筋分布相同的材料。

5 结语

综上所述，依据试验结果可得：

第一，第二层钢筋，即箍筋的实际保护层厚度会受到第一层钢筋，即分布钢筋间距的影响，且分布钢筋间距越大，那么箍筋的保护层厚度就会越小，反之则会越大。

第二，研究成果显示，率定公式计算值和实际测量值之间存在的误差较小，最大误差率也仅有1.4%。

第三，在施工现场，实际测量结果发现，率定公式修正值与凿孔实测值保持基本一致，由此证明率定公式的计算精准度可以满足工程施工的实际计算要求，可以广泛应用于分布钢筋保护层的测定工作。

第四，为切实保障率定公式修正值的精准性，在后续工作中应尽可能采用与现场测试构件规格参数一致的构件进行检测。