超临界流体水平流动换热中浮升力效应分析与判据评价
蒲星宇, 李舟航
(1.昆明理工大学 冶金节能减排教育部工程研究中心,昆明 650093;(2.昆明理工大学 冶金化工节能环保技术国家地方联合工程研究中心,昆明 650093)
符号说明:
cp——比定压热容,J/(kg·K)
d——管径,m
g——重力加速度,m/s2
G——质量流速,kg/(m2·s)
h——比焓,kJ/kg
p——压力,MPa
ρ——密度,kg/m3

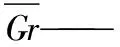
μ——动力黏度,Pa·s
q——热流密度,kW/m2
Re——雷诺数
T——温度,℃
ΔT——壁温差,K
x——沿管长坐标,m
λ——热导率,W/(m·K)
ν——运动黏度,m2/s
K——对流传热系数,kW/(m2·K)
下标
b——主流
c——临界
pc——拟临界
w——壁面
top——顶部
btm——底部
近年来,涉及超临界压力流体流动换热的工业过程受到了广泛应用。典型的涉及流体超临界状态的工业过程有:水作为超临界、超超临界压力化石燃料发电厂的工作流体[1-2],核反应堆冷却液[3],二氧化碳作为超临界萃取系统萃取剂[4],碳氢燃料作为火箭发动机燃料等[5]。
为提高相关超临界系统的经济性、效率和安全性,了解工作条件下的流动传热规律,针对流体在超临界压力管道内的流动传热特性,许多学者对此进行了大量实验和理论研究,但研究多集中于竖直流动,有关水平流动的研究较少。Cheng等[6-8]研究了超临界流体在管内的流动和传热行为。笔者对常用的超临界压力水平管中浮升力判据进行对比和评价,筛选出较为优秀的浮升力判别式,并提出了修正该判别式应遵循的原则。
1 浮升力影响下的超临界压力水平流动传热特性
Pioro等[8]对2007年之前的实验数据进行了总结,这些实验所用工质多为水和CO2,且大多研究的是竖直圆管内垂直流动。这是因为水平管内周向温度分布不均,研究难度较大。在超临界压力水平流动的研究中,已发现在热流量小或质量流量大的工况下,水平管内上下母线壁温相近,壁温周向分布均匀。当流体处于大比热容区时,会出现传热增强现象,流体传热系数随主流温度靠近拟临界点而同步增大,且在拟临界点附近达到最大值[9]。上述水平管工况中,上壁面与下壁面流体传热系数分布均匀,下壁面比上壁面稍高;此时,浮升力对换热的影响很小,对流传热系数的峰值是由流动边界层比热容的峰值引起的。这一点已被Yu等[10]、Tian等[11]的研究所证实。随着压力升高,流体大比热容区内比热容的峰值会随之下降,拟临界点附近流体传热系数峰值也迅速下降,其中在q/G较小工况下尤其明显。图1给出了不同操作压力下R134a实验段中对流传热系数的变化情况[11]。
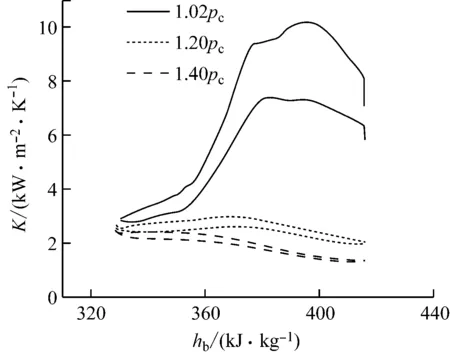
图1 不同操作压力下R134a实验段中对流传热系数的变化
在q/G较小工况下,浮升力效应不明显,比热容是流体传热系数变化的主导因素;在q/G较大工况下,浮升力的影响不能被忽略。水平管内流体被加热时,管道内近壁面流体与管中心相比温度更高,密度更小,管内截面上的流体因为径向温度梯度产生密度梯度而使浮升力影响显现,增加了超临界压力流体传热特性的复杂性[10]。而大比热容区内流体物性发生剧烈变化,使得浮升力效应更显著,因此有必要对水平管内这一现象进行研究。目前,大部分学者认为处于管中心的高密度低温流体受重力作用向管底部运动,增强了管内下半部分的流动性,使得传热系数增大,传热增强,而上半部分高温低密度流体流动性差,传热系数较小从而传热恶化,造成壁温的周向分布不均。
综上所述,将水平管内超临界流体的传热行为按q/G分为两类:q/G较小时,超临界流体在拟临界区热物性的急剧变化导致流体传热系数的变化;q/G较大时,影响传热行为的主要原因是通道截面上径向温度梯度产生的密度梯度,导致浮升力的变化。
除压力外,也有学者研究了管径对浮升力的影响。Cheng等[12]认为不管浮升力影响是否被忽略,管道截面内不均匀的速度分布是传热恶化的条件。在浮升力影响不能被忽略的工况下,从主流到边界层中产生的一对对称涡旋导致cp小的流体聚集在管内顶部。随着管径增大,由热物性导致的热加速效应被抑制,浮升力的影响更显著,有更大的空间形成涡旋。因此,大管径下顶部的传热恶化与底部的传热增强都更明显,同一截面位置处顶部与底部壁温差(以下简称壁温差)较大,可视作浮升力效应存在的直观证据。
2 数值模拟研究存在的问题
有学者通过数值模拟对水平管内浮升力的影响进行研究,比较了不同模型管内顶部壁温模拟值与实验值之间的差异。Tian等[11]发现对于超临界R134a,AKN湍流模型拟合程度较好;Liu等[13]发现对于超临界水,SST湍流模型拟合程度较好;Zhao等[14]和Yang[15]研究得出对于超临界CO2,LB模型拟合程度较好。但是这些模型都存在同样的问题,如图2所示,首先这些模型都只在主流温度处于拟液区时与实验值相关性较好,一旦主流温度跨过拟临界点,内壁面温度实验值高于模拟值,因此利用数值模拟对拟气区流动传热机理进行分析具有局限性。其次,在较大q/G工况下,模拟值与实验值差距较大,因为q/G较大时,浮升力影响更强,说明现有的模型只能反映小q/G条件下cp为主导的传热流动过程,并不能很好地反映浮升力影响下的流动与传热机理。为保证所参考文献研究结论的准确性,笔者在涉及大q/G及主流处于拟气区时,仅使用前人的实验数据进行研究。
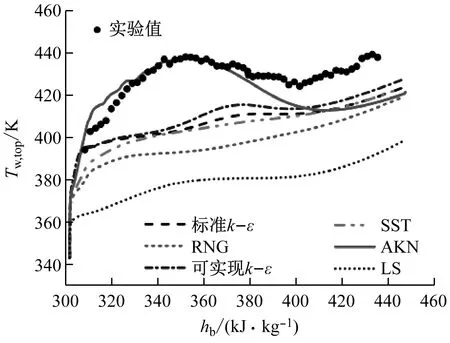
图2 R134a管顶部壁温实验值与各模型模拟值的对比[11]
3 浮升力影响判别式
目前,针对不同浮升力关联式的分析来看,尚未提出令人满意的预测水平管浮升力影响程度及其范围的判别式。表1给出了常用判别式。

表1 常用水平管浮升力判别式
针对超临界CO2的研究中,Liao等[19]将Grb/Re2>0.001作为浮升力导致的二次流在管内流动中不能被忽略的阈值,大管径下当(Tb/Tpc)<1.01时判别式值大于阈值,当(Tb/Tpc)>1.01时判别式值小于阈值,并且判别式值的量级随管径增大而增大。由于判别式值与管径d成正比,因此管径导致的管内努塞尔数Nu改变是小管径下浮升力影响较小的原因之一。吕海财等[20]对浮升力准则进行了归一化研究,得出BuJ沿管长方向呈先增大后减小的趋势,在管径2 mm的管道中BuJ值远大于阈值,由此可知以该判别式评估浮升力影响过于保守。
Bazargan等[21]利用水平管中超临界水的实验数据对比了Gr/Re2>0.1、Gr/Re2.7>10-4、Grq/Grth>1 3种判别式。整体来说,主流温度接近Tpc时,判别式的定性温度选取很重要,选取管道顶部内壁面温度能更好地反映浮升力的影响。在选取0.1作为Gr/Re2的阈值时,发现在某些工况下,即使判别式的峰值小于阈值,浮升力效应仍可通过水平管顶部和底部巨大的壁温差来反映,因此认为该公式适应性不好。对于Gr/Re2.7这一原本用来判断垂直管浮升力影响的判别式,即使在浮升力可被忽略的工况下,其值也远大于阈值10-4。
而对于Grq/Grth,当壁温差增大时,该判别式的量级随之增大。并且该公式成功反映了壁温差表征的浮升力影响先增强,在Tb接近Tpc时达到峰值,而后下降至趋于恒定这一特性。在文献[21]的实验中,对浮升力影响最小的一组实验数据,判别式的值整体处于1~5范围内,并且该判别式能够预测仅为4 K的最大壁温差。因此,该判别式精确地判断了浮升力的影响范围。Bazargan还研究发现,通过对同一组实验数据选取顶部与底部内壁面温度作为Grq/Grth定性温度并不影响该判别式的整体变化趋势,仅仅峰值有微小差别。
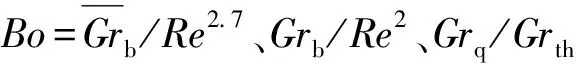
对不存在明显传热恶化但壁温差明显的工况,几种判别式的量级均较小,但仅有Grq/Grth成功预测了壁温差的峰值。对浮升力可忽略的工况,整体壁温差小于3.5 K的,Bo值远小于阈值10-5,但另2种判别式的值仍然大于阈值,Tian认为在这种工况下这些判别式的阈值需要重新被讨论。
4 对Grq/Grth判别式的评价
综合前人对判断浮升力影响的判别式进行对比评价后发现,普遍认为Grq/Grth的效果最好。但笔者认为,该判别式仍有其局限性。
4.1 定性温度选择
Bazargan认为计算Grq/Grth时,选取顶部或底部的内壁面温度作为定性温度对计算结果影响不大,二者只是在峰值附近数值略有差异,整体趋势不变,几乎相同的位置都趋于同一定值。但该结论具有很强的局限性。在其管径为6.6 mm的实验中,顶部和底部的温度变化趋势大体相当,壁温差最大值不超过12 K,这是导致选取顶部或底部内壁面温度作为定性温度计算Grq/Grth变化趋势大体相当的原因。然而在Yu等[23]的实验中,有一组工况与该实验入口温度、q/G、压力等参数均相同,仅改变管径至26 mm,对这组工况进行分析,如图3所示,在实验入口段与Grq/Grth峰值位置,选取顶部与底部内壁面温度作为定性温度计算得出的Grq/Grth值均相差一倍,且二者峰值位置对应的主流焓值相差很远。从Grq/Grth的构成来进行分析,Grq包含d4项,因此受管径影响很大,大管径下顶部与底部壁温的差异会导致计算结果差异被放大。而大管径下浮升力的影响更显著,顶部传热恶化与底部传热增强都更明显,顶部温度变化剧烈而底部温度变化缓慢。由于温度变化导致的物性变化曲线的差异,使得计算得出的Grq/Grth峰值对应的主流焓值有巨大差异。所以对于Grq/Grth,选取顶部温度作为定性温度来进行计算更具普适性。
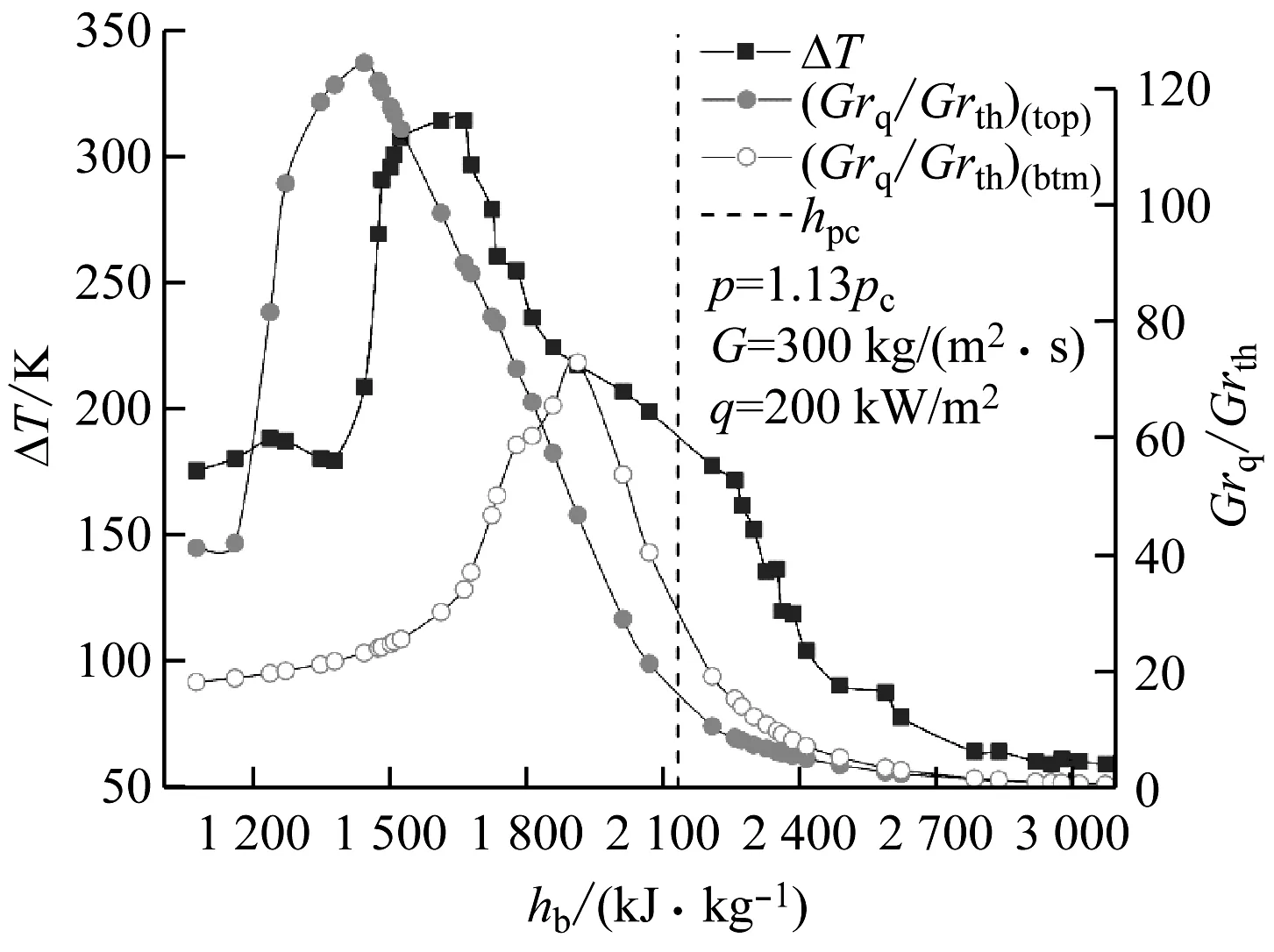
图3 水在不同定性温度下Grq/Grth与壁温差的变化
4.2 Grq/Grth在拟气区的局限性
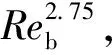
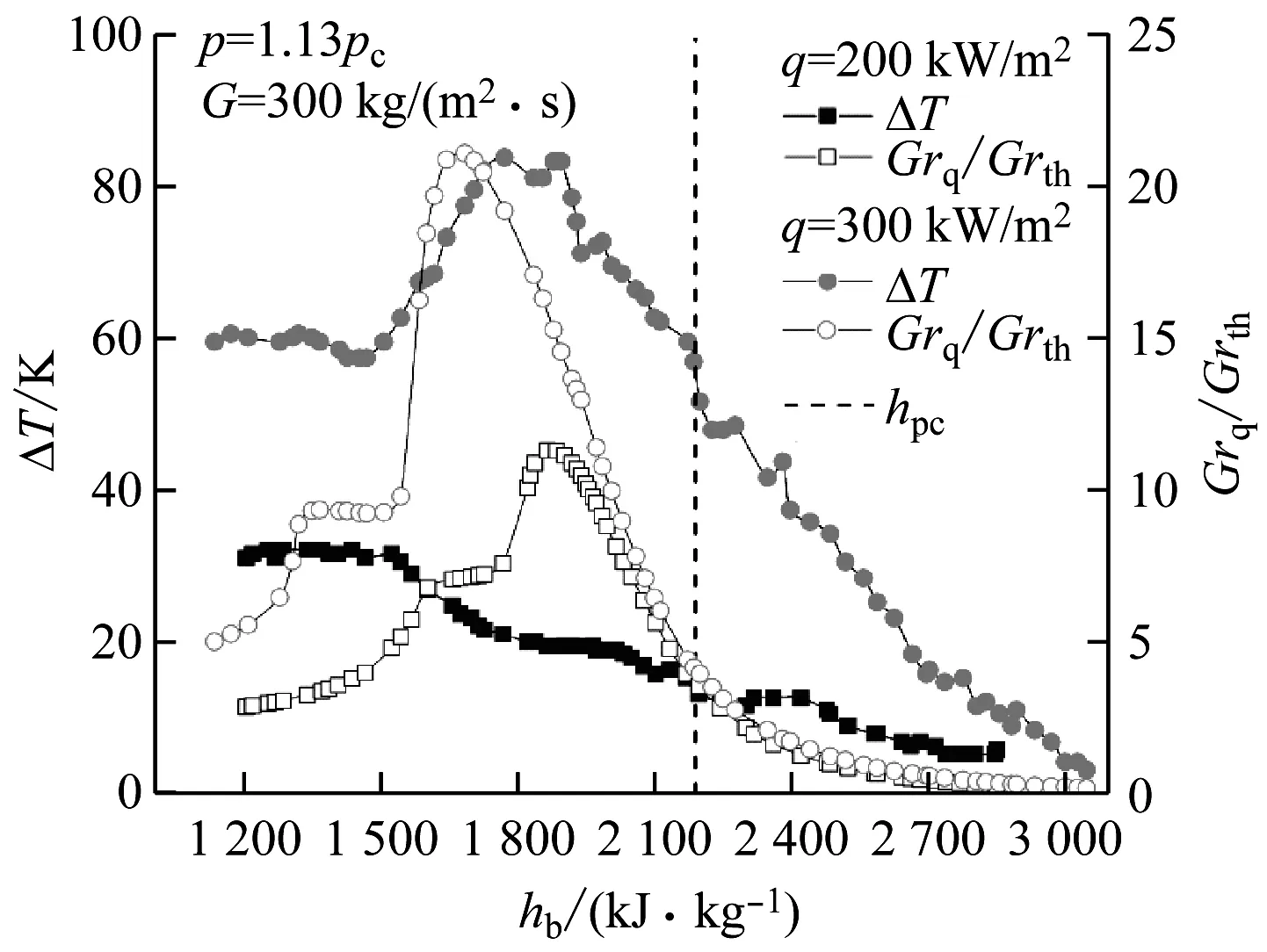
图4 水在不同热流密度条件下Grq/Grth与壁温差的变化
同理,当拟液区与拟气区壁温差基本相同时,Grq/Grth的值相差较大。以文献[22]的数据为例进行分析,如图5所示。当壁温差在拟液区和拟气区均为37.5 K左右时,拟液区Grq/Grth的值为117,而在拟气区仅为1.8。无论q/G如何变化,Grq/Grth在拟气区总会趋于1左右的定值,而拟液区Grq/Grth的量级会随着q/G的增大而增大。同时,当壁温差在拟气区为37.5 K时,Grq/Grth已达到近似恒定,然而根据巨大的壁温差可以判断此时浮升力的影响仍旧明显,所以不能通过Grq/Grth在拟临界点两侧数值上的一致性来判断浮升力的影响在两侧是否相同,也无法对Grq/Grth提出单一阈值来判断浮升力的影响是否可被忽略。
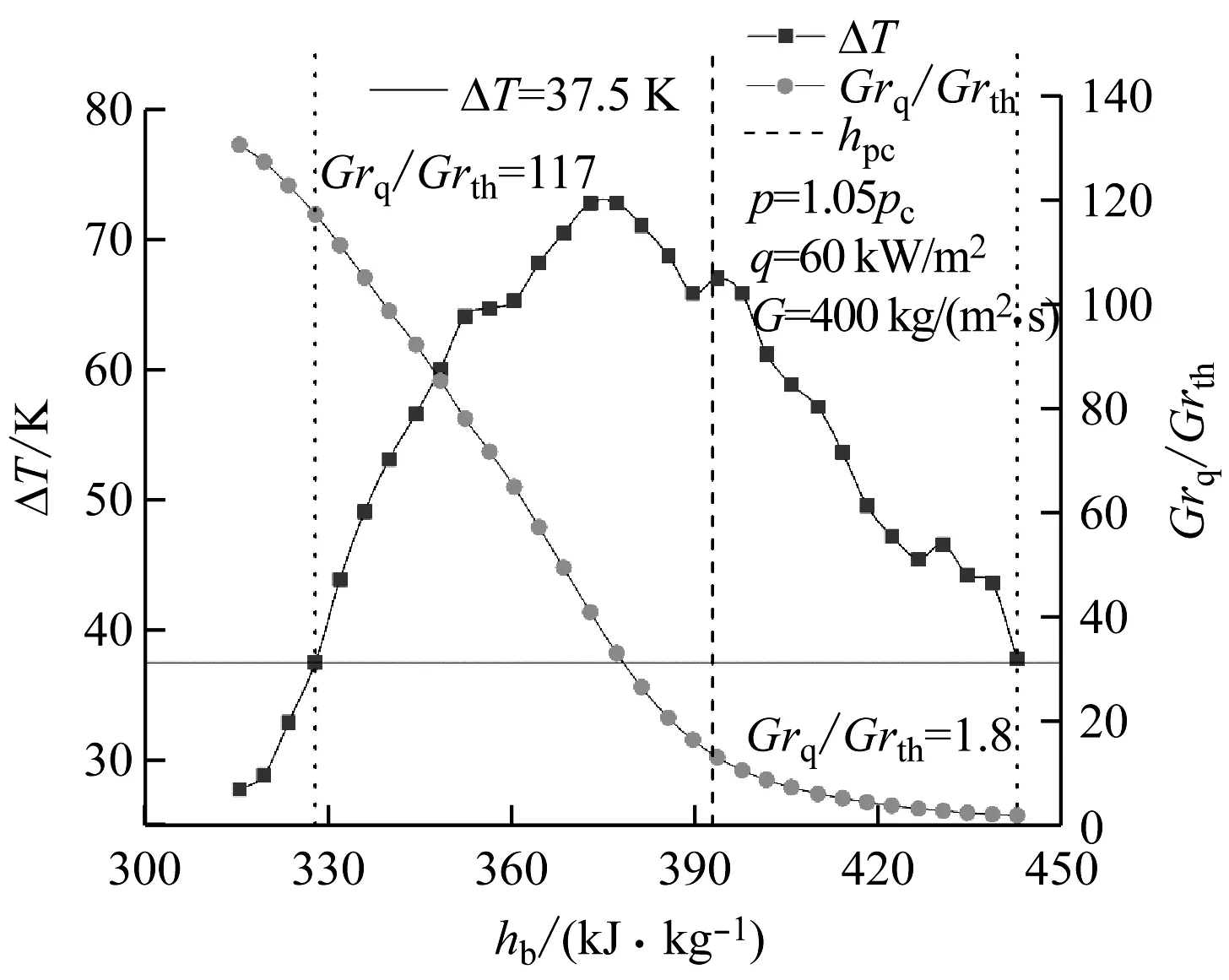
图5 R134a在拟液区和拟气区Grq/Grth和壁温差的对比
4.3 Grq/Grth与壁温差峰值位置的相关性
文献[23]中,判别式Grq/Grth成功预测了浮升力影响条件下壁温差的变化趋势。图6中,以超临界水为介质时,Grq/Grth的变化趋势与壁温差的变化趋势一致。在主流温度处于拟液区时,壁温差曲线与Grq/Grth曲线均在接近Tpc位置有峰值,然后当主流温度超过Tpc后迅速下降并趋于恒定。
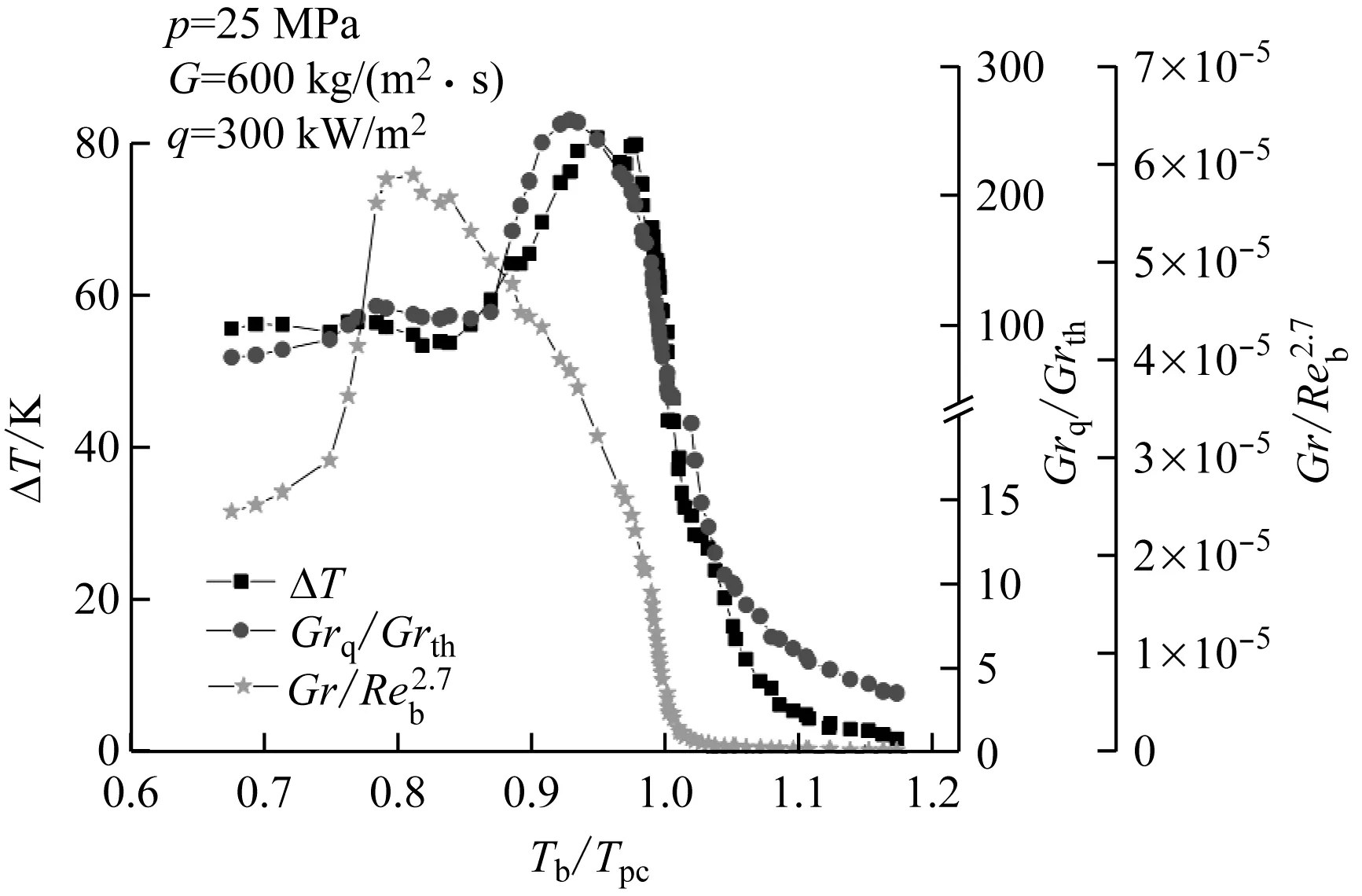
图和Grq/Grth随Tb/Tpc的变化[23]
Tb/Tpcof water[23]
Tian等[24]对不同热流密度下cp对水平管内换热的影响进行了分析,如图7所示。随着热流密度的增大,主流与壁面之间的温度梯度也随之增大,主流与壁面间径向大比热容区宽度变窄,导致因大比热容区cp剧烈变化而对传热产生的影响逐步减弱,直至浮升力成为影响换热的主要因素。因此,壁温差峰值与Grq/Grth峰值对应的流体焓值变化趋势一致,二者均随热流密度增大远离拟临界点焓值hpc。但对大量实验数据进行分析后发现,实际情况恰好相反,随着热流密度增大,所有工质均出现壁温差峰值与Grq/Grth峰值所对应的流体焓值变化方向相反的特性。如图8所示,利用文献[18]的实验数据进行计算得出,随着热流密度增大,壁温差峰值处的流体焓值hb逐渐靠近hpc,而Grq/Grth峰值处的hb逐渐远离hpc,这两者对应的hb的差值随热流密度增大而增大。
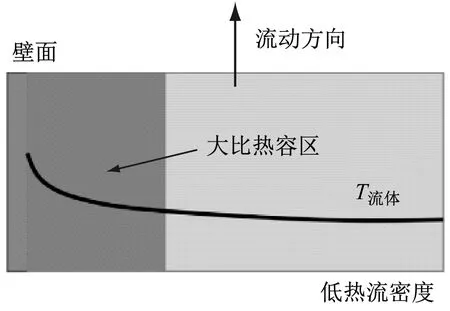
图7 不同热流密度下cp对水平管内换热的影响[24]
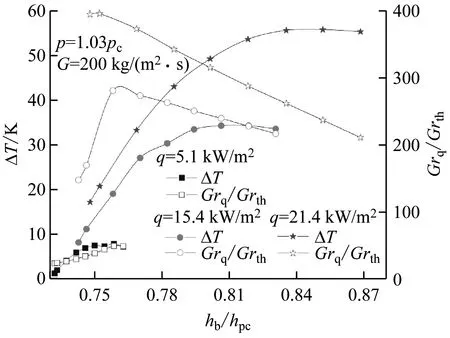
图8 CO2在不同热流密度下Grq/Grth与壁温差的变化
之前的学者只分析了不同q/G下,管内壁面顶部传热恶化、底部传热增强的程度与管内整体对流传热系数变化趋势,而忽略了对浮升力峰值位置的判断。这是因为壁温差大小一定程度上可以表征浮升力的大小,所以其峰值代表了浮升力峰值的位置,不同工况下壁温差峰值位置的改变代表了浮升力峰值位置的变化。因此,Grq/Grth用来描述壁温差的变化趋势具有局限性,Grq/Grth虽能大致反映壁温差的整体变化趋势,但不能准确预测壁温差峰值位置。
4.4 管径对Grq/Grth的影响
由于实验条件限制,管径对浮升力影响的实验研究较少,笔者选用文献[22]的实验数据进行分析。从图9可以看出,图中的大管径约为小管径的1.6倍,而壁温差和Grq/Grth在2组管径下的变化比值也约为1.6倍,且改变管径后二者仍拥有相同的变化曲线与峰值位置。随着管径增大,壁温差和Grq/Grth均明显增大,这与之前的增大管径会增大浮升力影响的结论相符。从该角度分析,当建立一组壁温差与Grq/Grth的数值对应关系,改变管径后该对应关系仍大致成立,然而从图9可以看出,二者峰值对应的hb位置相差很大。随hb的增大壁温差逐渐增至最大值,然后逐渐下降;而Grq/Grth的值在入口附近已达到最大。这一变化趋势在4.3节已有分析,事实上其与热流密度有关而与管径无关。因此,可以判定不同管径下Grq/Grth与壁温差的变化具有一致性,可判定该判别式对不同管径适应性较好。
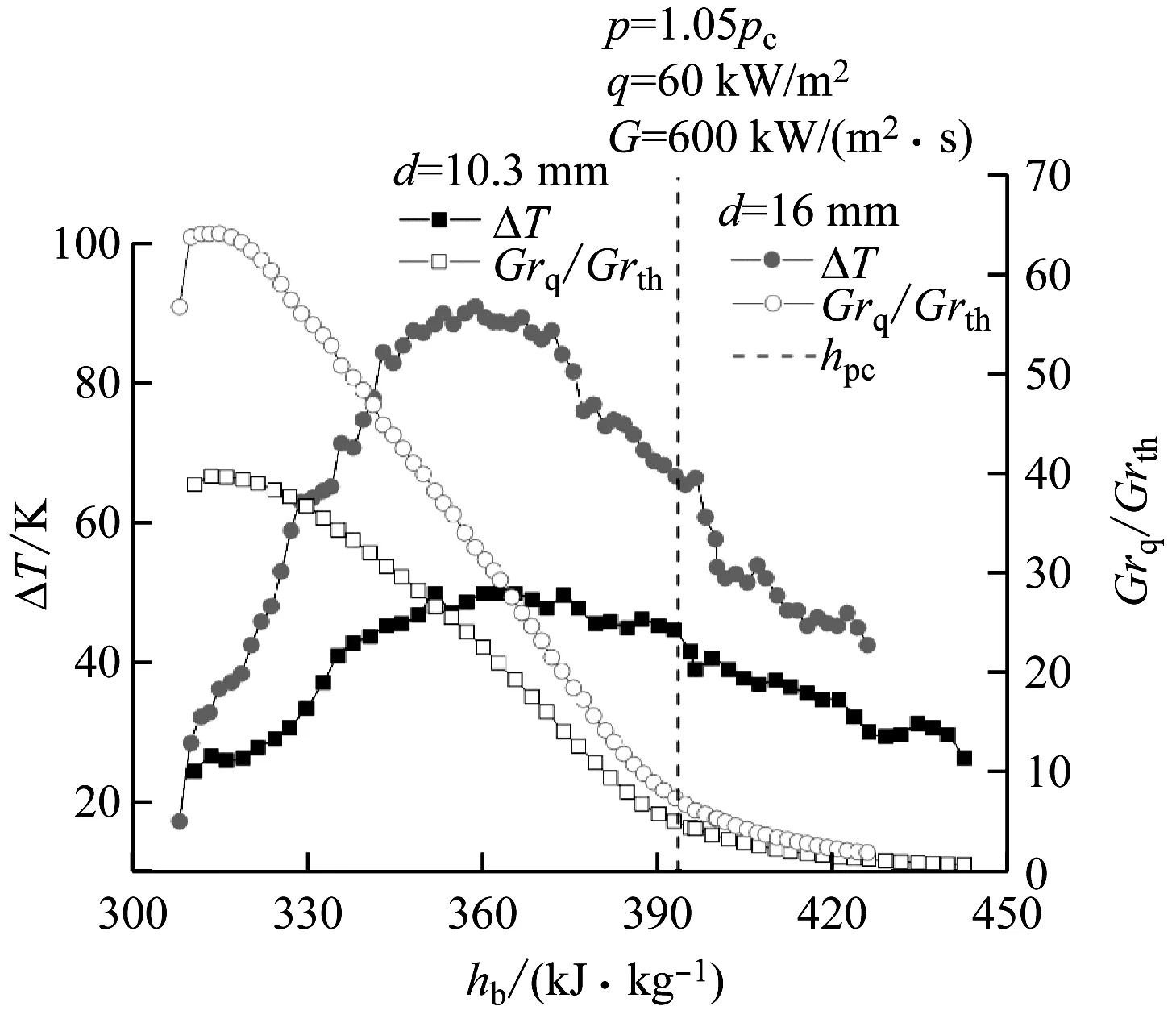
图9 R134a在不同管径下Grq/Grth与壁温差的变化
4.5 修正Grq/Grth应遵循的原则
虽然有待进一步研究,但基于Grq/Grth的局限性,可得出对该公式进行修正应满足的一些要求。基于Grq/Grth在拟气区的局限性,对其修正后,不同热流密度下浮升力的影响程度应明显反映在Grq/Grth的值上;在拟液区和拟气区,当该判别式值相同时,通过壁温差表征的浮升力影响程度应相当,以提出一个在拟液区和拟气区均适用的阈值来判断浮升力影响是否可被忽略。基于不同热流密度下壁温差峰值处hb的变化趋势,修正Grq/Grth后不仅要反映不同热流密度下浮升力的影响程度,也要预测浮升力的沿管发展。即不同热流密度下Grq/Grth峰值与壁温差峰值处hb的位置应大致相同,以便预测管内浮升力的影响程度以及传热恶化程度最深的位置。
5 结 论
(1)虽然普遍认为判别式Grq/Grth在水平管浮升力准则关联式中效果最好,对管径变化的适应性较好,但仍有一定局限性。对大部分工况而言,只能选取顶部温度作为计算的定性温度;在拟气区不同热流密度条件下,浮升力影响与Grq/Grth的值没有对应关系;无法对Grq/Grth提出单一阈值来判断浮升力的影响是否可被忽略。
(2)通过分析实验数据发现,随着热流密度增大,壁温差峰值处hb逐渐靠近hpc,除了通过壁温差来判断浮升力影响程度外,该数值也是衡量管内浮升力发展状况的一个重要因素。
(3)为使判别式Grq/Grth具有普适性,对其进行修正后,该公式应满足:不同热流密度下浮升力的影响程度应明显反映在Grq/Grth的值上;当Grq/Grth的值在拟液区和拟气区相同时,二者通过壁温差表征的浮升力影响程度应相当;不同热流密度下,其峰值处hb的变化趋势应与壁温差峰值处hb的变化趋势相同。

