在线社交超网络的信息全局传播模型
巩云超,李发旭,周丽娜,胡 枫*
(1.青海师范大学计算机学院 西宁810008;2.青海省藏文信息处理与机器翻译重点实验室 西宁810008;3.藏语智能信息处理及应用国家重点实验室 西宁810008)
随着互联网的发展与普及,以QQ、微信、微博、Twitter、Facebook为代表的在线社交平台,使数以亿计的互联网用户不再受时间、地域的限制就能够快速发布、接收和分享信息。同时,在线社交网络中信息传播的速度快和范围广的特点,给信息传播带来了前所未有的影响。因此,研究在线社交网络中信息传播的机理及规律,对网络中信息传播的预测和控制有着重要的理论依据和现实意义。
鉴于在线社交网络中的信息传播过程类似于传染病传播过程,以传染病传播模型为基础建立的信息传播模型的研究最为广泛[1-2],经典模型有SIS模型[3]、SIR模型[4-5]、SIRS模型[6]和SEIR模型[7]。在此基础上,许多信息传播模型被提出,如H-SEIR模型[8]、SHIR模型[9]和ESIS模型[10]等。与此同时,信息传播过程中的影响因素也被分析,如记忆效应与社会强化效应[11-13]、节点属性与信息价值[14-16]和节点影响力[17-18]等。目前,关于信息传播的研究主要基于普通图结构构建在线社交网络,但这类网络并不能准确地描述在线社交网络中的群聚特性。例如,在微信或QQ中,用户可以私发信息给某个好友用户,也可群发信息到多个社交群组;在微博中,用户能同时被多个用户所关注。当用户发布或转发一条信息时,其被关注群组中的多个用户都能够转发和评论该信息。为了更精准地描述真实在线社交网络中用户之间复杂的社交关系和信息交互行为,文献[19]引入了超图中的超边表示多个个体之间的群聚关系,且考虑反应过程策略和接触过程策略,提出了两种策略下的SIS信息传播模型。文献[20]基于超图的超网络模型构建动态社交超网络,建立了一种基于SIS的信息传播模型。
迄今为止,超网络中信息传播模型的研究均在文献[21]提出的超网络演化模型基础上构建社交网络,该模型每次增加多个用户与网络中已存在的单个用户组成社交群组。分析现实在线社交网络,更多的情形是用户与网络中已存在的多个用户组成社交群组,即基于BA无标度的超网络演化模型更契合现实在线社交网络的群组特性。针对这一问题,本文在文献[22]提出的基于BA无标度网络的超网络动态演化模型基础上构建在线社交超网络,结合基于反应过程策略的SIS模型,对在线社交超网络中信息全局传播过程进行理论分析和仿真实验。
1 相关理论
1.1 超网络相关概念

设 Ω=(V,E)是 有限超图,G是 从[0,∞)到 Ω的映射,则对于给定的t≥0,G(t)=(V(t),E(t))是一个有限超图[24]。超网络G(t)是 一个随时间t演化的超图集合,其中,节点vi的超度dH(i)定义为该节点所在超边的数量。例如在线社交超网络中,节点代表个体,超边代表个体参与的社会关系,如朋友关系、家人关系、同学关系、同事关系等,节点的超度表示个体参与的社会关系数量。如图1所示超网络,节点集合V={v1,v2,v3,v4,v5,v6,v7,v8,v9},超边集合E={e1,e2,e3,e4,e5},其 中e1={v1,v2,v3,v4,v5},e2={v1,v2,v3,v4,v6},e3={v3,v4,v5,v6,v7},e4={v1,v3,v4,v5,v8},e5={v2,v3,v6,v7,v9}。节点v1和v2同属于超边e1,则 节 点v1和v2邻 接,超 边e1和e4的 交 集 为{v1,v3,v4,v5},则 超 边e1和e4邻 接。|ei|=5(i=1,2,3,4,5),则该超网络为5一致超网络。节点v1和v4的超度分别为3和4。
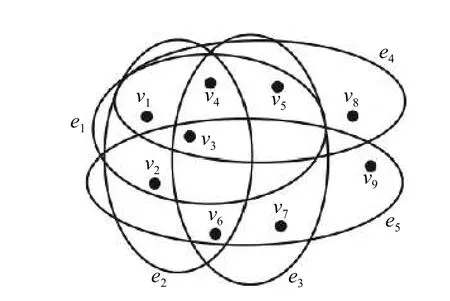
图1 超网络示意图
1.2 RP策略的SIS模型超网络相关概念
反应过程策略(reactive process strategy,RP)[25-26]表现为全局传播,即初始传播节点所在的所有超边中的节点均为初始传播节点的邻居节点,并对所有邻居节点进行信息传播。例如,在企业微信群中,领导在本部门群组中发布信息,那么该群组中所有员工都能够接受并传播该信息。基于RP策略的SIS模型描述如下:
1)网络中的个体划分为易感者(S状态)和染病者(I状态)。
2)初始时,随机选择网络中的一个或者多个节点为染病者,其他节点均为易感者。
3)每个时间步内,染病者与其相邻的所有易感者接触后,染病者依照事先设定的概率β将易感者感染为染病者,该概率β被称为传播率。同时网络中的染病者依照事先设定的概率 γ将染病者治愈为易感者,该概率 γ被称为恢复率,治愈后的易感者仍有可能会再次感染变成新的染病者。
4)随着疾病在网络中不断传播,染病者所占密度将会达到一个相对稳定值,并在这个相对稳定值附近进行小幅度波动,这意味着网络中的疾病传播达到稳定状态,简称为稳态。
2 超网络中的信息全局传播
2.1 超网络的构造过程
在线社交超网络模型构建基于文献[22]提出的BA无标度超网络演化模型,构造算法如下:
1)初始化:初始时网络中包含m0个个体,这m0个 个体构成一种社交群组关系,即m0个节点构成一条超边。
2)增长:每个时间步t内,添加一个个体,新加入的个体与超网络中的m1个已存在的个体构成一种新的社交群组关系,即新添加的节点与m1个旧节点构成一条新超边。
3)优先连接:从已有的超网络中按照超度优先选取m1个旧节点,与新添加的节点结合生成超边。每次选取连接的节点vi的概率 Πd H(i)等 于节点vi的超度dH(i)与超网络中的已有节点vj的超度dH(j)总和之比,即:
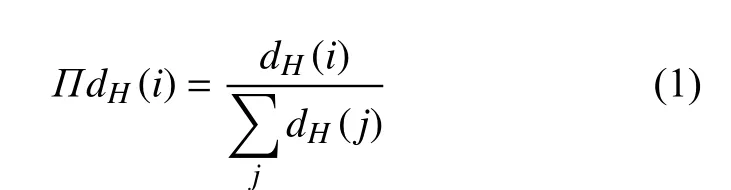
式中,d H(i)为节点vi参与的超边数量,即为节点vi的超度。
超度分布P(k)[22]指超网络中超度为k的节点在整个网络中所占的比例,经过t个时间步后,超网络中节点的超度分布独立于时间t,P(k)为:

2.2 超网络中的信息全局传播过程
根据信息在社交群组中传播的特点,在线社交超网络中信息全局传播的动态过程可以近似地用基于RP策略的SIS模型来描述。
1)在线社交超网络中的个体划分为不知情者(S状态)和知情者(I状态)。其中,不知情者为尚未获得信息或者不关心且不愿意传播信息的个体,知情者为已获得信息并愿意继续向其他人传播信息的个体。
2)初始时,从超网络中随机选择一个节点为传播节点,该节点为超网络中第一个获得信息的知情者,处于I状态,其他节点则处于S状态。
3)每个时间步内,超网络中处于I状态的节点向其所在超边中的所有邻接节点传播信息。其中,处于S状态的节点以概率β接收信息后转变为I状态,处于I状态的节点以概率γ 恢复到S状态。
4)随着信息在网络中不断传播,处于I状态节点所占密度将会达到一个相对稳定值,并在这个相对稳定值附近进行小幅度波动,这意味着网络中的信息全局传播达到稳态。
信息全局传播过程描述如图2所示。其中,黑色节点表示该个体处于S状态,白色节点表示该个体处于I状态。t=0时刻,超网络中的全部节点处于S状态;t=1时刻,从超网络中随机选择一个节点(编号为v5) 处于I状态;t=2时刻,由于节点v5被超边e1、e3和e4所包围,所以其邻接节点v2、v7和v8获得信息处于I状态;t=3时刻,由于节点v2、v5、v7和v8被 超边e1、e2、e3、e4和e5所包围,所以其邻接节点v1、v3、v6和v9获 得信息处于I状态,而节点v2和v5恢 复为S状态。
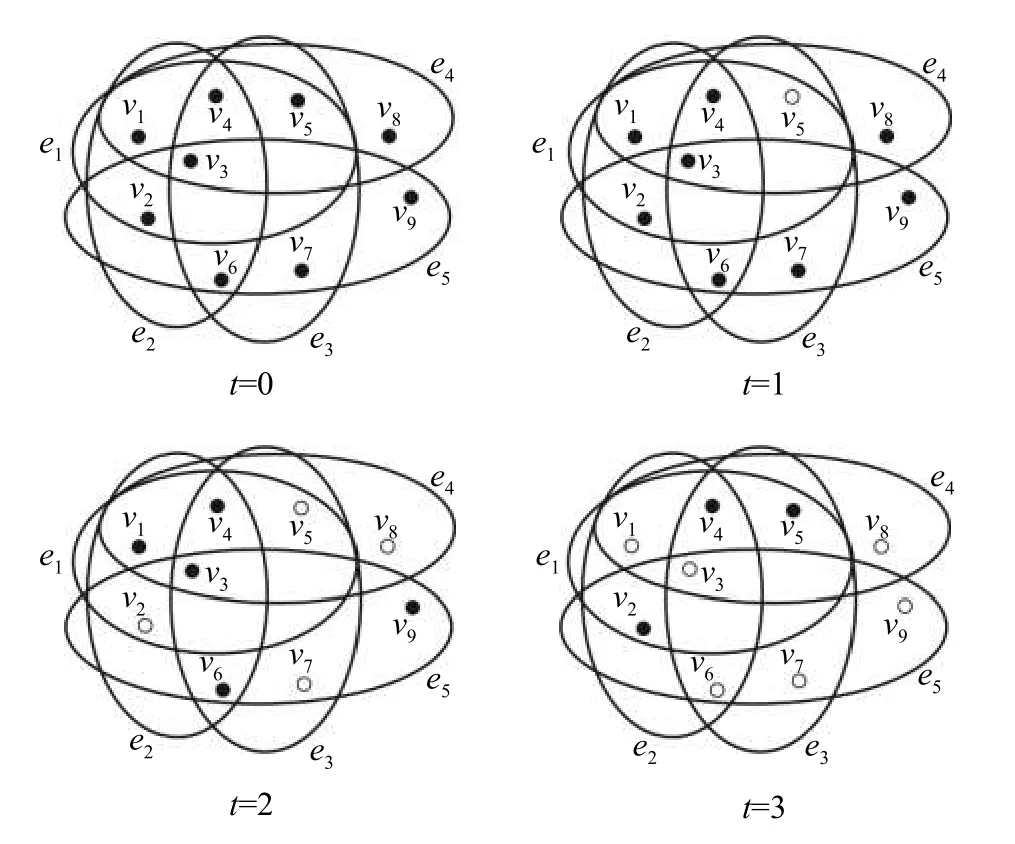
图2 超网络结构下的信息全局传播示意图
2.3 理论分析
根据平均场理论,超网络中的信息全局传播动力学的平均反应速率方程可记为:
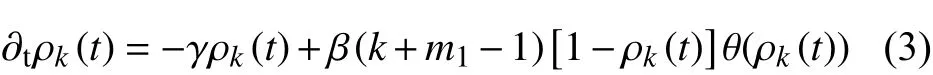


式(4)表明邻居数越多的节点,其被感染的概率越大,获得信息的机会越高。
在 θ(β,γ)的计算中,超边中超度为s的节点的概率与sP(s)成正比,因此:

解式(7)可得:
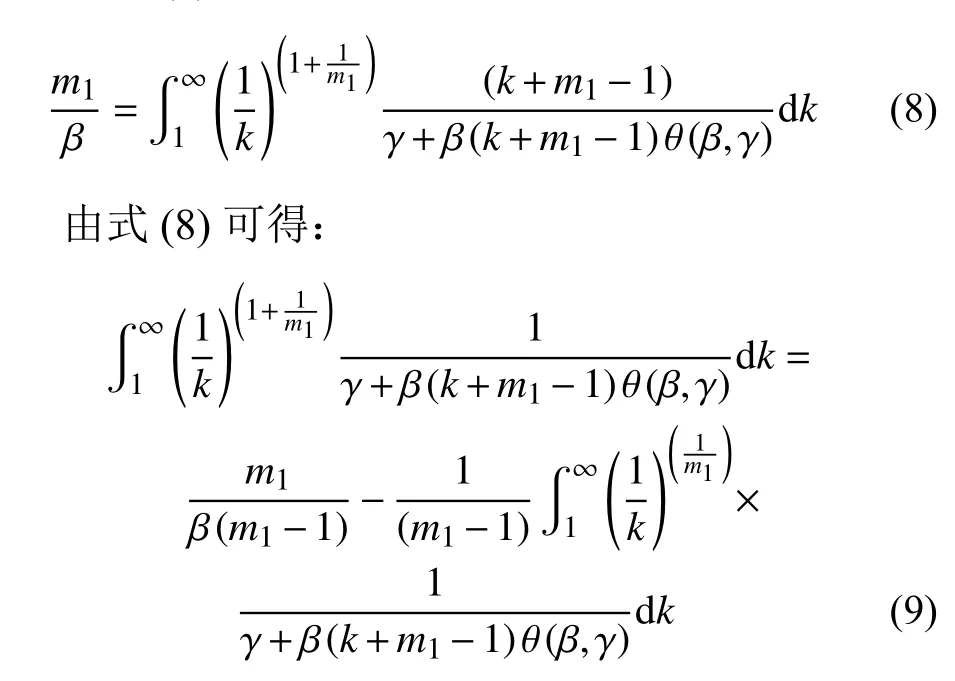
其中式(9)左项为:

结合式(9)和式(10),可解得:
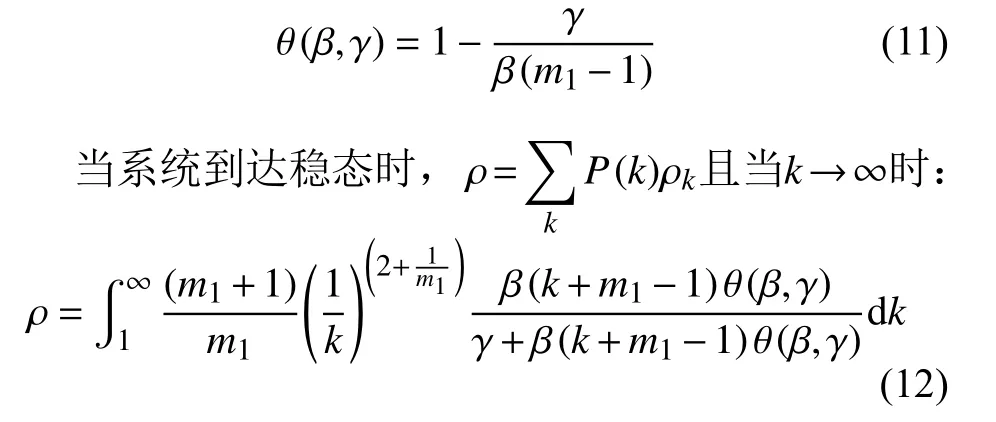
由式(12)可得:
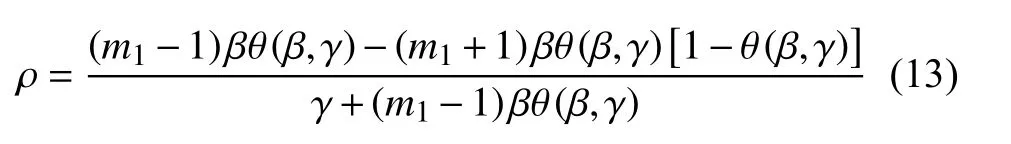
式(13)表明,信息在超网络中的全局传播到达稳态时,ρ是一个独立于时间t的函数。如果已知超网络的传播率、恢复率和网络结构等参数,就能得到超网络中I状态节点的密度ρ。
3 仿真分析
采用2.1节中的方法构造在线社交超网络,在模型构造过程中每个时间步内添加的超边数也可扩展到m条。依据2.1节的构造算法,本文对在线社交超网络中信息全局传播的动态过程进行了计算机仿真。仿真实验侧重于超网络规模N、传播率β、恢复率γ、新节点进入时选择旧节点数m1和生成的超边数m,以及初始传播节点对超网络中信息全局传播的影响,同时对超网络和复杂网络结构下的信息全局传播的动态过程进行了对比分析。为了消除随机影响,以下每组仿真实验都是在相同初始条件下,独立重复运行50次取均值的结果。
3.1 不同参数下的理论结果与稳态仿真结果
固定参数为N=1 000,m0=4,6,8,m1=3,5,7,m=1, γ=0.06。图3为不同参数下模型的理论结果与稳态下仿真结果的对比图。仿真过程直到达到稳态结束,获得知情节点所占密度ρ。根据式(13)计算理论值,图3中曲线为理论结果,离散点为仿真结果。在不同参数下,理论结果与仿真结果相吻合。随着传播率β值逐渐增大,信息在超网络中的全局传播到达稳态时,知情节点所占密度越大,波及范围越广。即使传播率很小,信息也会传播到整个网络。

图3 理论结果与稳态下的仿真结果
3.2 超网络规模 N对信息全局传播的影响
为描述信息全局传播的动态过程,获得知情节点所占密度随时间的变化趋势。固定参数为m0=4,m1=3,m=1, β=0.3, γ=0.06。图4为不同超网络规模下的信息全局传播曲线。超网络中节点总数分别为1000、5000和10000时,3条曲线几乎是重叠的,信息在超网络中的传播时间和稳态下知情节点所占密度基本一致,表明超网络规模对信息全局传播的动态过程的影响极小。因此,下面的仿真实验均在N=1 000的超网络结构中进行。

图4 不同超网络规模下的信息全局传播曲线
3.3 传播率β、恢复率γ 对信息全局传播的影响
固定参数为N=1 000,m0=4,6,8,m1=3,5,7,m=1,测试传播率、恢复率对信息全局传播的影响。在线社交超网络中信息全局传播的动态过程分为前期增长阶段和后期稳定阶段。传播率代表个体的信息传播能力,传播率β值越大,信息全局传播的速度越快,波及范围越大。恢复率代表个体对信息的抵抗能力,恢复率 γ值越大,信息全局传播的速度越慢,波及范围越小。
1)传播率β 的影响
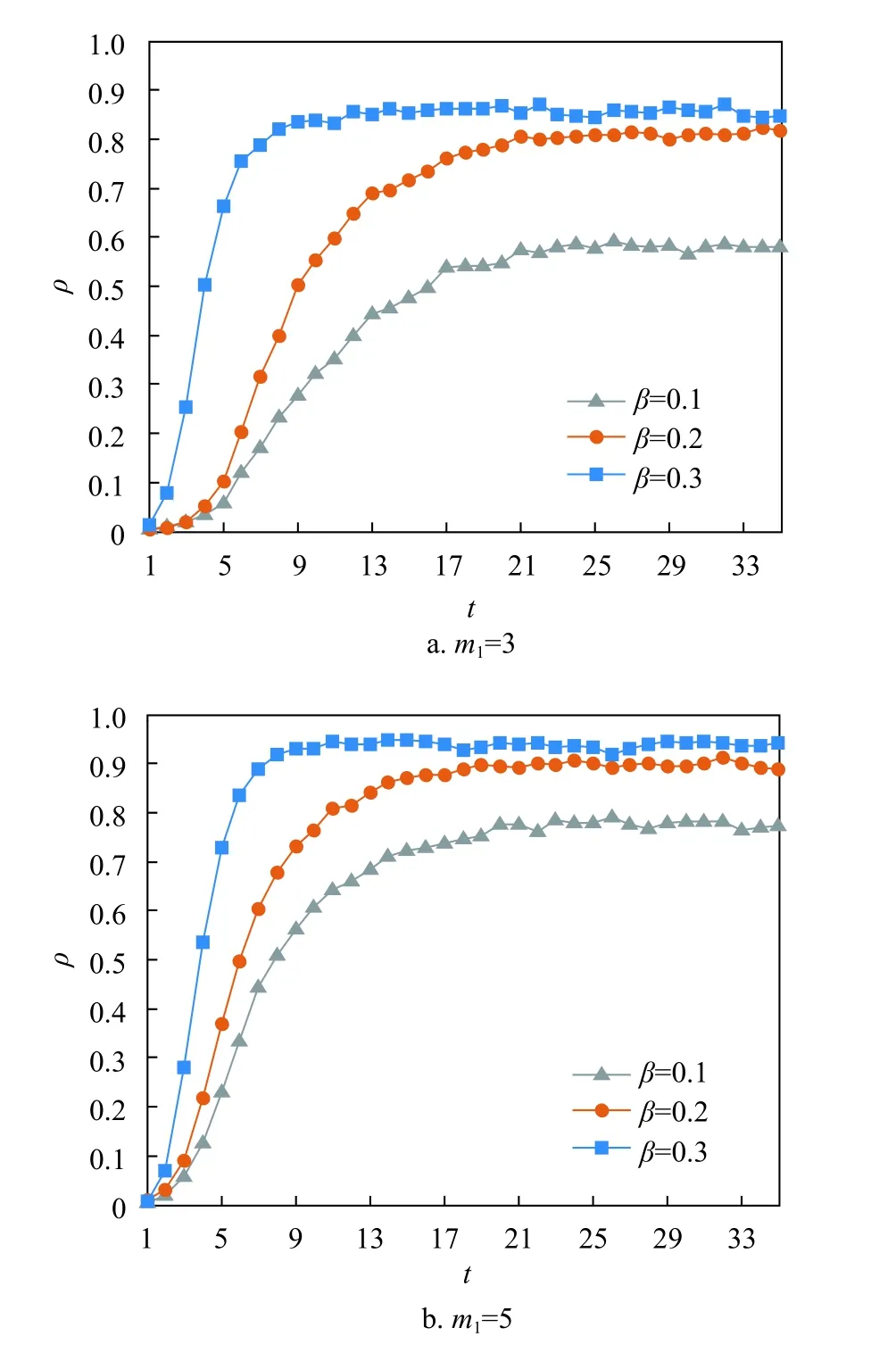
图5所示传播率 β=0.1,0.2,0.3,恢复率γ=0.06时,在线社交超网络中知情节点所占密度随时间的变化趋势。如图5所示,对于不同的传播率,信息在超网络中的传播行为极其相似。随着传播率β逐渐增大,即个体的信息传播能力逐渐增强。前期增长阶段,知情节点所占密度到达稳态时所需时间步逐渐减小,即不知情节点获得信息的时间逐渐缩减,信息传播的速度逐渐加快。到达稳态时峰值逐渐增大,即信息的波及范围逐渐扩大。后期稳定阶段,知情节点所占密度到达稳态,并在峰值附近进行振幅较小的波动。随着信息在超网络中不断传播,一部分处于I状态的个体将进入遗忘期,恢复为S状态,而恢复为S状态的个体可能会再次获得信息进入I状态。由此可见,信息一旦在超网络中传播,就会扩散到整个超网络。
2)恢复率γ 的影响
图6为恢复率γ =0.06,0.1,0.2,传播率 β=0.3时,在线社交超网络中知情节点所占密度随时间的变化趋势。如图6所示,对于不同的恢复率,信息在超网络中的传播行为极其相似。随着恢复率 γ值逐渐增大,即个体对信息的抵抗能力逐渐增强。前期增长阶段,知情节点所占密度到达稳态时所需时间逐渐增大,到达稳态时峰值逐渐减小。后期稳定阶段,知情节点所占密度到达稳态,并在峰值附近进行振幅较小的波动。由此可见,随着恢复率 γ值逐渐增大,网络中知情节点所占密度逐渐下降。
由图5和图6在不同的m1值显示的传播曲线可以看出,相同传播率和恢复率下,随着超边中旧节点数量m1逐渐增大,知情节点所占密度到达稳态时的时间逐渐减小,表明信息的传播速度越来越快,也就是说超边中所含的节点数目越多,意味着每个时间步内可能感染的个体会越多,即使传播率很小,信息也能够在短时间内迅速波及扩散到整个网络。

图5 不同传播率下的信息全局传播曲线
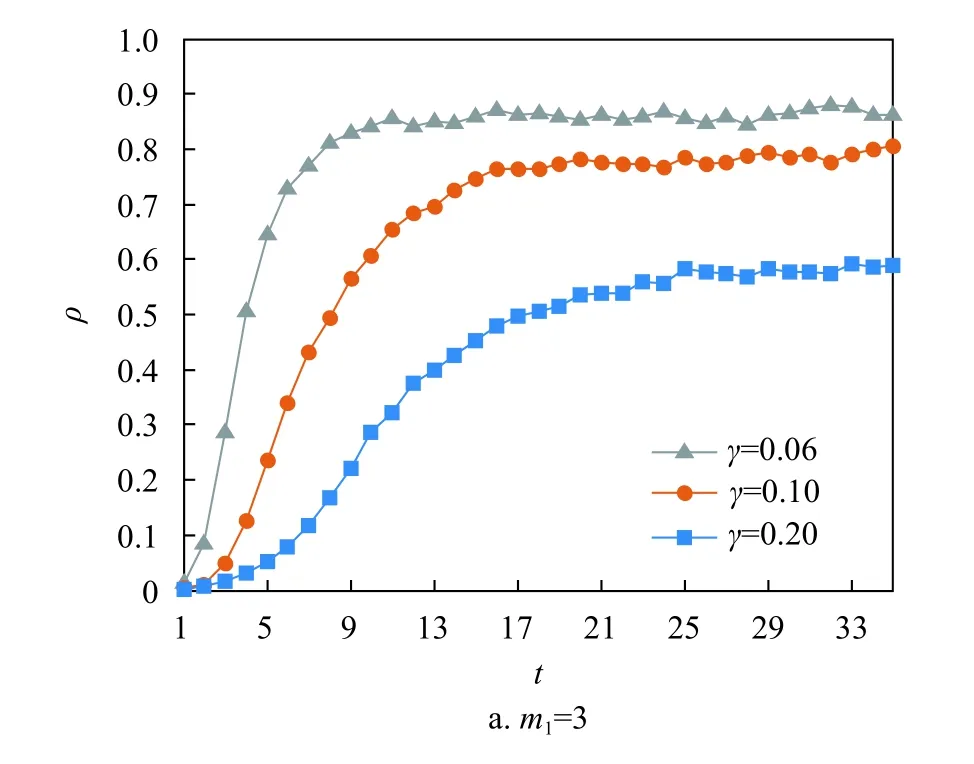

图6 不同恢复率下的信息全局传播曲线
3.4 超网络结构参数对信息全局传播的影响
固定参数为N=1 000,m0=4,6,8,m1=3,5,7,β=0.4, γ=0.06,测试超网络结构参数m1和m对信息全局传播的影响。m1表示超网络中新节点进入时选择的旧节点数,m1值越大,意味着节点所在超网络中的邻居越多。m表示超网络中新节点进入时生成的超边数,m值越大,意味着节点所参与的社交群组越多。图7为m=1,2,3时,在线社交超网络中知情节点所占密度随时间的变化趋势。如图7所示,对于不同的m1和m,信息在超网络中的传播行为极其相似。随着m1和m值逐渐增大,前期增长阶段,知情节点所占密度到达稳态时所需时间逐渐减小,到达稳态时峰值逐渐增大。后期稳定阶段,知情节点所占密度到达稳态,并在峰值附近进行振幅较小的波动。由此可见,个体在超网络中的邻居越多,参与的社交群组越多,都将会使个体有更多的机会获得和传播信息,即个体获得和传播信息的速度越快,信息的波及范围越广。
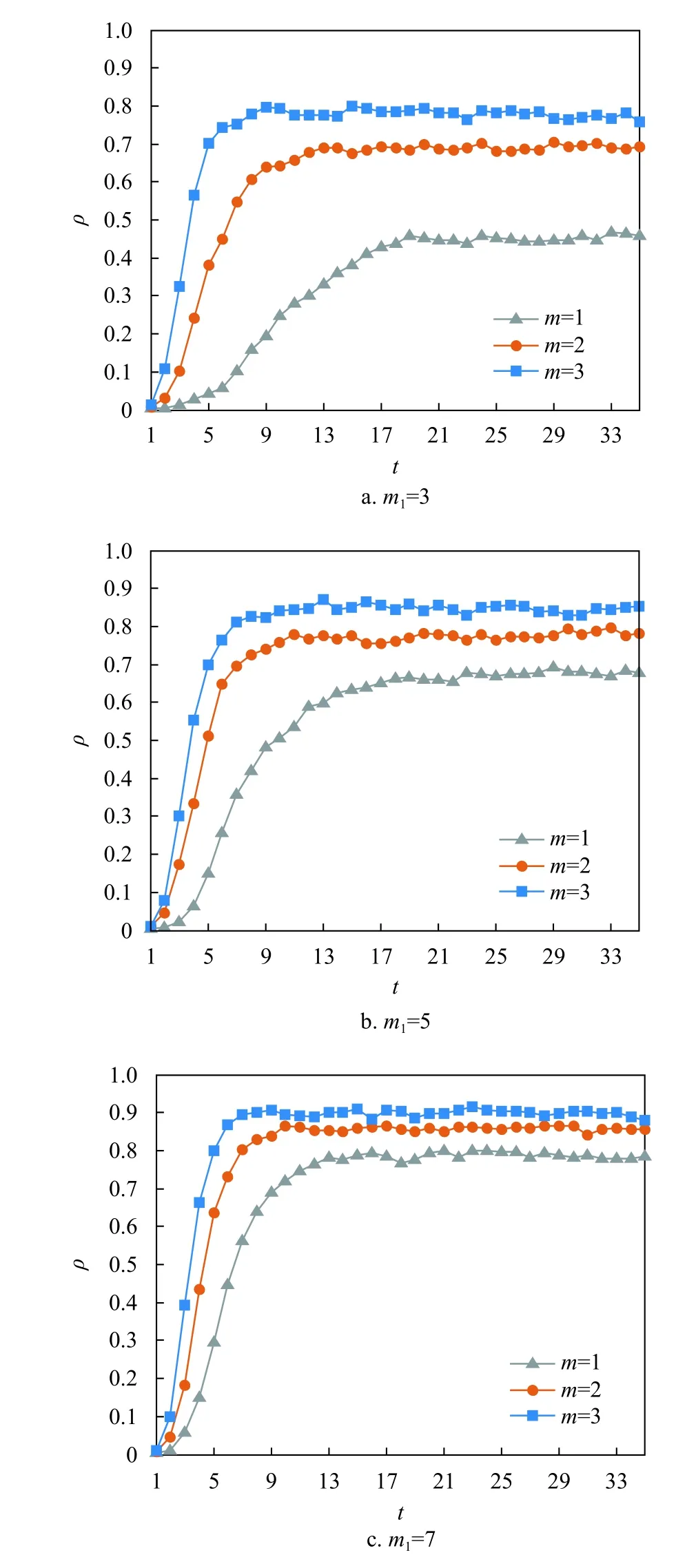
图7 不同m下的信息全局传播曲线
3.5 初始传播节点对信息全局传播的影响
固定参数为N=1 000,m0=6,m1=5,m=1,分别选择超度值最大的节点(超度最大值为309,节点编号为14)和超度值最小的节点(超度最小值为9,节点编号为195)作为初始传播节点进行仿真实验。如图8所示,初始传播节点的选择只对信息全局传播的前期增长阶段存在影响,不影响后期稳定阶段。前期增长阶段,参数设置为β=0.1,γ=0.06的情况下,选择超度值较大的节点作为初始传播节点,到达稳态时所需时间较少,而选择超度值较小的节点作为初始传播节点,到达稳态则需要一定时间;参数设置为β=0.3, γ=0.06的情况下,选择超度值较大的节点与选择超度值较小的节点到达稳态的时间差很小。后期稳定阶段,两种情况分别收敛到相同的值。根据节点超度的定义可知,超度值大的节点会出现在多条超边中,对应于现实生活中个体具有多种社交关系,具有较大的传播影响力。例如在线社交网络中的名人、明星和大V发表的信息能够在网络中迅速传播,造成较大的社会影响。
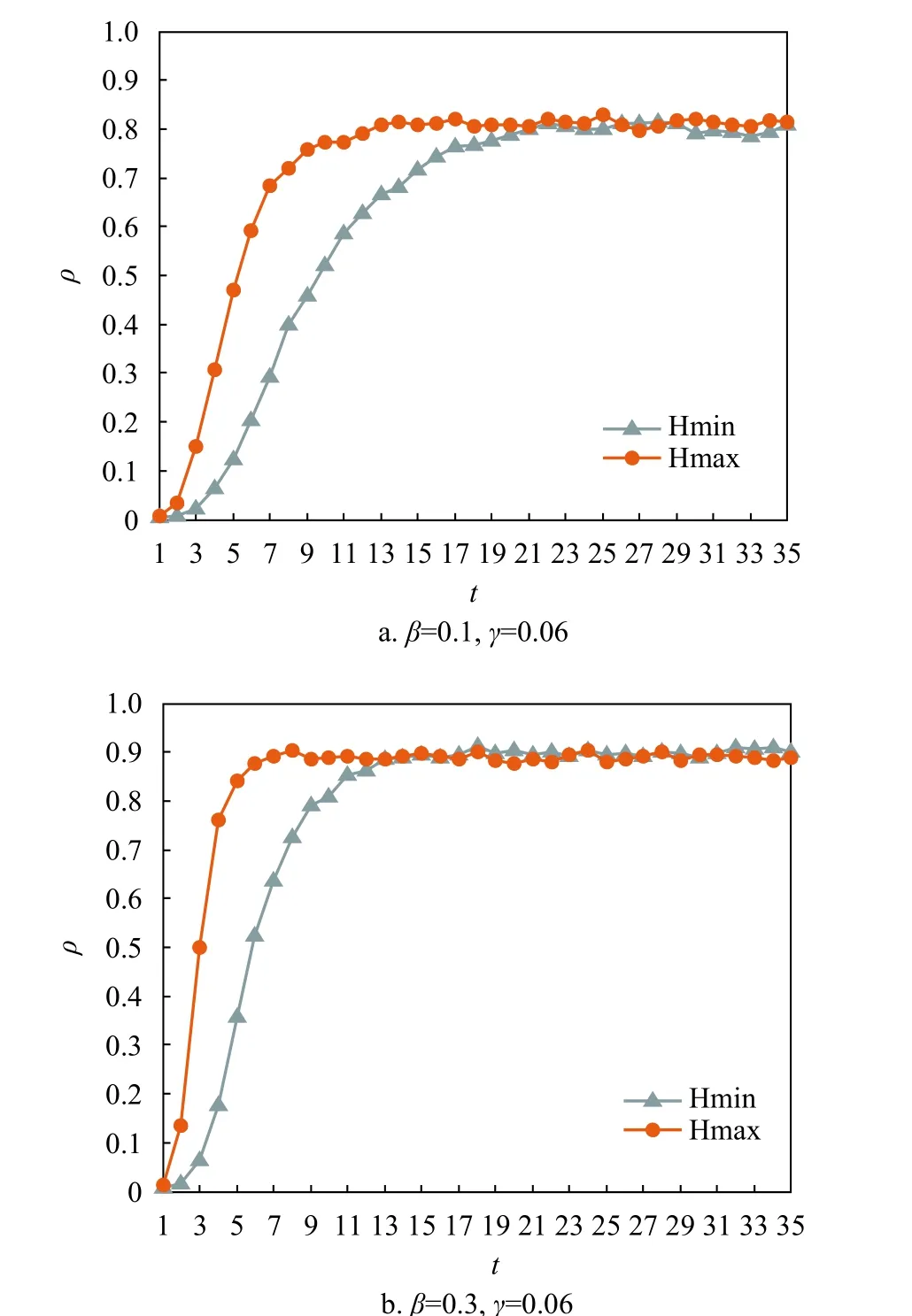
图8 不同初始传播节点下的信息全局传播曲线
3.6 超网络和复杂网络结构下信息全局传播对比
针对信息在不同网络结构下的全局传播过程,分别生成两个规模为1000的网络:复杂网络和超网络。复杂网络按照BA模型构造,其中参数设置为m=2。超网络按照2.1节模型构造,其中参数设置为m0=6,m1=5,m=2。固定参数为传播率β=0.4,恢复率γ =0.06。图9为两个网络结构下的信息全局传播曲线。如图9所示,复杂网络结构中的信息全局传播需要一定时间,而超网络结构中的信息能够迅速扩散到整个网络,同复杂网络结构相比较,超网络结构下的信息全局传播到达稳态时,波及范围较广,即获得信息的人数较多。事实上,复杂网络中每个个体只受其邻居节点的影响,而超网络中每个个体都会受到社交关系中其他所有邻居的影响。因此,超网络结构中的信息全局传播能够更精准地反映在线社交网络中信息传播的规律。
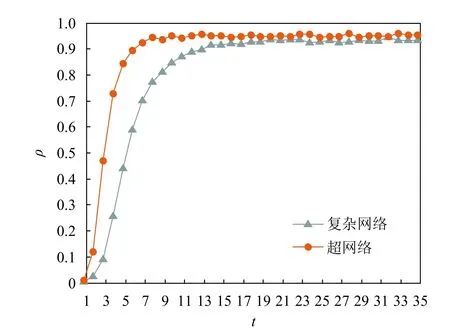
图9 不同网络结构下的信息全局传播曲线
进一步,超网络按照2.1节模型构造,其中参数设置为m0=2,m1=1,m=2。固定参数传播率β=0.4,恢复率γ=0.06。如图10所示,在传播率、恢复率相同的情况下,超网络和复杂网络中的信息全局传播曲线在前期增长阶段和后期稳定阶段基本吻合。仿真结果表明,当超网络结构参数设置为m0=2,m1=1,m=2时,该超网络模型就退化为BA模型。因此,BA模型上的信息全局传播可视为本文模型的特例。
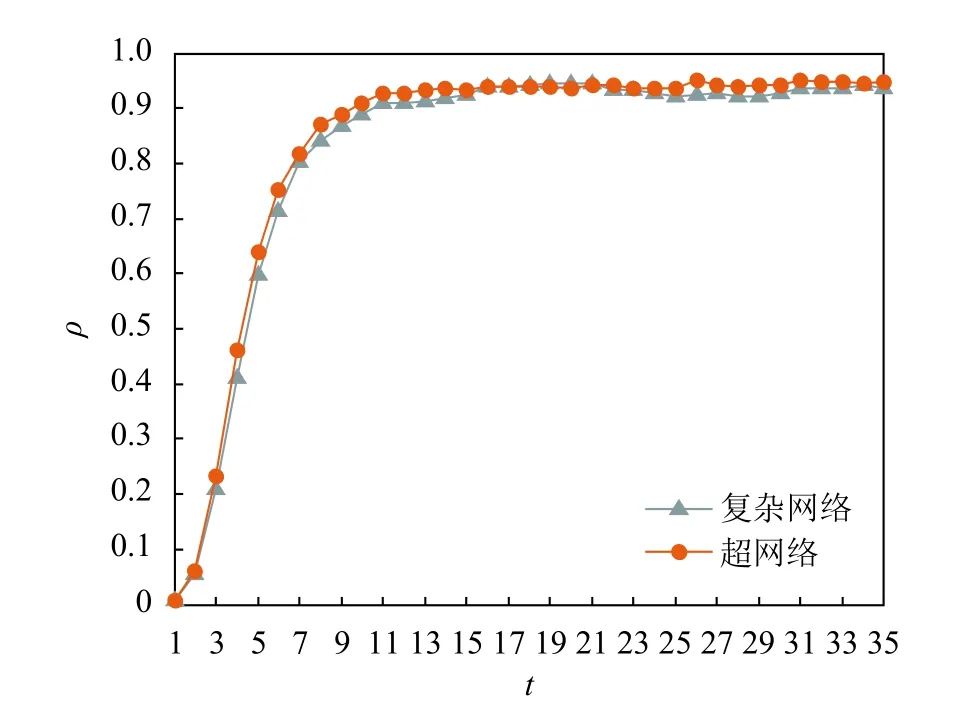
图10 退化的超网络和复杂网络结构下的信息全局传播曲线
4 结束语
本文为刻画现实在线社交网络中的信息全局传播规律,在基于BA无标度网络的超网络动态演化模型的基础上构造在线社交超网络,结合基于RP策略的SIS模型,研究了超网络结构下的信息全局传播的动态过程。仿真发现,理论分析和仿真实验完全吻合。超网络的规模对信息全局传播的影响极小,而传播率和恢复率不仅影响信息在前期增长阶段的传播,还影响信息在后期稳定阶段的传播。超网络中新节点进入时每次选择的旧节点数和每次生成的超边数越多,信息传播速度越快,波及范围越广。初始传播节点的选择只对信息在前期增长阶段的传播时间存在影响,不影响信息在后期稳定阶段的传播。同复杂网络结构相比,基于超图结构的超网络中的信息全局传播速度更快,波及范围更广。本文的研究侧重于在线社交超网络的信息传播的动态过程,而信息传播的动态过程往往受多种复杂因素的影响,如信息的时效性、个体的从众心理等等。研究复杂因素下的信息传播规律并建立验证模型,以及在真实网络数据上展开研究将是今后的研究方向。

