基于改进元胞自动机模型的地铁车厢乘客疏散模拟
周美琦,杨晓霞,张纪会,刘天宇
(1.青岛大学自动化学院复杂性科学研究所,山东 青岛 266071;2.青岛理工大学机械与汽车工程学院,山东 青岛 266525)
0 引言
近些年,城市轨道交通发展迅速,地铁已经成为备受大众欢迎的交通方式之一,它不仅极大地方便了人们的出行,还充分利用了地下空间,缓解了地面交通压力。通常,地铁车辆行驶于地下隧道内,一旦发生突发事故,需要就近找地铁站紧急停车,然后再进行乘客疏散,情况较为复杂。尤其是在上下班高峰期或者节假日期间,车厢内人员密集,在疏散过程中极易在地铁车厢车门处产生瓶颈效应,增加疏散时间,使得人员疏散更加困难。因此,地铁站车厢内发生突发事故时乘客的疏散应格外受到重视。

在利用元胞自动机模型研究行人的疏散行为时,行人的运动主要与元胞到出口的距离以及行人之间的相互作用有关,通常需要建立相应的静态场模型和动态场模型进行描述。Zhu等人[27]根据二维摩尔邻域元胞自动机模型建立了行人运动规则,研究了具有不对称出口布局的房间内行人的疏散行为。Song等人[28]利用改进的元胞自动机模型模拟人群的运动,再现了人群在疏散过程中出现的“成拱”以及“快即是慢”现象。Zheng等人[29]提出了基于元胞自动机模型的改进地板场模型,研究了地铁站发生洪水情况下乘客的疏散行为。

然而,上述借助元胞自动机模型模拟行人疏散的研究中,与地铁突发事故相结合的较少。在行人出口选择的相关研究中,忽略了影响出口选择因素与行人出口选择行为之间的非线性关系。模糊逻辑理论可以很好地解决这类具有非线性关系的变量问题,且善于模仿人脑的不确定性概念判断、推理思维方式与经验,这也是本文选择采用模糊逻辑理论解决车厢内乘客车门选择问题的重要原因。本文基于元胞自动机模型提出了地铁车厢内乘客的疏散运动模型,并基于模糊逻辑理论构建了乘客的车门选择模型,用以模拟突发事故时地铁车厢内乘客的疏散行为,具有无需建立复杂数学模型以及计算简单的优势,兼顾了效率和准确性。
1 模型
1.1 元胞自动机模型


图1 摩尔型邻域的元胞自动机模型示意图
将地铁车厢内的区域划分为元胞,每个元胞的坐标用(i,j)表示。本文中规定每个元胞有两种状态:1)元胞被占据(本文所研究的地铁突发事故是以火灾为例,所以这里指元胞被火源、座椅或乘客占据);2)元胞为空闲。每个乘客下一时刻的移动位置由到邻胞的转移概率Pij决定,由式(1)和(2)计算得到。
Pij=Nexp(KSSij)exp(KDDij)(1-ηij)
(1)
N={Σexp(KsSij)exp(KDDij)(1-ηij)}-1
(2)
在转移概率Pij中,Sij和Dij分别表示每个元胞(i,j)的静态场值和动态场值,Ks和Kd分别为静态场和动态场的比例系数。ηij表示元胞(i,j)是否被占据。当元胞被占据时,ηij=1;否则,ηij=0,如式(3)所示。
(3)
根据式(1)和(2)计算出每个元胞向周围元胞的转移概率,乘客将选择具有最大转移概率的元胞作为自己下一步的目标移动位置。当乘客周围的8个元胞都被占据时,乘客将停留在原来的元胞位置不动。
1.2 乘客运动模型
当地铁车厢内发生突发事故时,受到本能的趋利避害心理影响,乘客通常是向距离车门近而又尽可能远离事故点的位置移动。同时,也存在部分心理素质较差的乘客,受恐慌情绪影响,其判断能力明显下降,故而出现从众现象。
在上述元胞自动机模型中,静态场Sij可表示元胞(i,j)对乘客的吸引力。本文以地铁突发事故中发生频率最高的火灾事故为例,当地铁车厢发生火灾时,乘客可移动位置到火源的距离d1以及到车门的距离d2对于其逃生非常重要。当一个元胞距离火源越远且距离车门越近时,该元胞的静态场值就越大。本文中定义每一个元胞(i,j)的静态场值如式(4)所示。其中,(p,q)和(mk,nk)分别表示火源中心点占据的元胞坐标和每一节车厢车门占据的中心元胞坐标,x1,x2分别表示距离d1和d2的比例系数。本文研究的地铁车辆为B型车,其基本尺寸为:长19 m、宽2.8 m、高3.8 m,共有24个车门,故k∈[1,2,3,…,24],k的具体取值由后文中根据模糊逻辑理论判断乘客目标车门的选择来确定。
(4)
动态场Dij表示地铁车厢发生突发事故时乘客受周围乘客疏散路线的影响,即从众现象。用M(i,j,n)表示乘客邻胞n累计通过的乘客数量,其中n∈[1,2,3,…,8]。当经过某一个邻胞的乘客数量越多时,该邻胞的动态场值就越大。本文用式(5)表示每一个元胞(i,j)的动态场值[36]。
(5)
本文中静态场Sij的大小是根据乘客可移动位置到火源的距离以及乘客到车门的距离综合来确定,因此,为了更好地完善构建的模型,将式(4)计算得到的Sij带入式(6)中进行归一化处理,从而把Sij转化成了无量纲的数值。结合最终计算得到静态场Sij和动态场Dij,根据式(1)和(2)可得到转移概率,进而可确定乘客的最终移动的目标位置。
(6)
1.3 突发事故中地铁车厢内乘客的车门选择行为
乘客对于车门的选择在很大程度上会影响到整体疏散效率。一般而言,影响乘客车门选择的因素主要有以下三方面:1)乘客到车门的距离;2)车门到事故点(本文中指火源)的距离d4;3)车门周围乘客的密度(本文中密度定义为以车门中点为圆心,半径为1.5 m的半圆内乘客的数量与此半圆面积的比值)。乘客在车门选择的过程中,对所谓的距离远近、密度的大小并没有一个绝对的标准,即大于多少就是远,否则就是近。因此,本文中提到的d3,d4,ρ这3个因素属于模糊概念,传统一对一映射的方法不再适用,而基于模糊集和隶属度函数的模糊逻辑理论能够很好地处理这一类模糊问题。此外,模糊逻辑理论还具有不需要建立复杂的数学模型以减少计算量的优点。因此,本文选择采用该方法进行乘客车门选择问题的研究。
模糊逻辑理论一般由四部分组成,分别为:模糊化、规则库、模糊推理和去模糊化。模糊化是模糊逻辑理论的重要组成部分。它可将确定的输入值转换为相应的模糊语言变量值。这里的模糊语言变量是一个模糊集。对于车厢内乘客的车门选择行为,本文拟采用d3,d4,ρ这3个关键参数作为模糊推理系统的输入变量进行描述。
关于隶属度函数的确定,目前大多数模糊推理系统都是建立在经验和实验的基础上。本文根据仿真模拟动态演化规律并参阅文献[37],最终选取了最常用的高斯型隶属度函数进行模糊化。高斯型隶属度函数平滑且敏感性较强,对于本文所研究的乘客目标车门选择的问题适应性更强。本文中用Sd3,Md3,Ld3分别表示乘客到车门的距离d3为短、中、长;同理,用Sd4,Md4,Ld4分别表示车门到火源的距离d4为短、中、长。进而,引入以下两个模糊集{Sd3,Md3,Ld3}和{Sd4,Md4,Ld4}来表示d3和d4的状态。为方便计算,我们将地铁车厢的长度取为20 m,宽度取为3 m,得到距离d3和d4对应的隶属度函数如式(7)和(8)所示。
(7)
(8)
用Sρ,Mρ,Lρ分别表示车门附近乘客的密度为小、中、大,并引入模糊集{Sρ,Mρ,Lρ}表示其状态。ρ对应的隶属度函数如式(9)所示。
(9)
定义模糊逻辑系统的输出变量为p,表示乘客选择某个车门的模糊概率,并用模糊集{Sp,Mp,Lp}表示。其中,Sp,Mp,Lp分别表示乘客选择某个车门的模糊概率为低、中、高。输出变量p对应的隶属度函数由式(10)给出。各个模糊逻辑变量间的关系如图2所示。
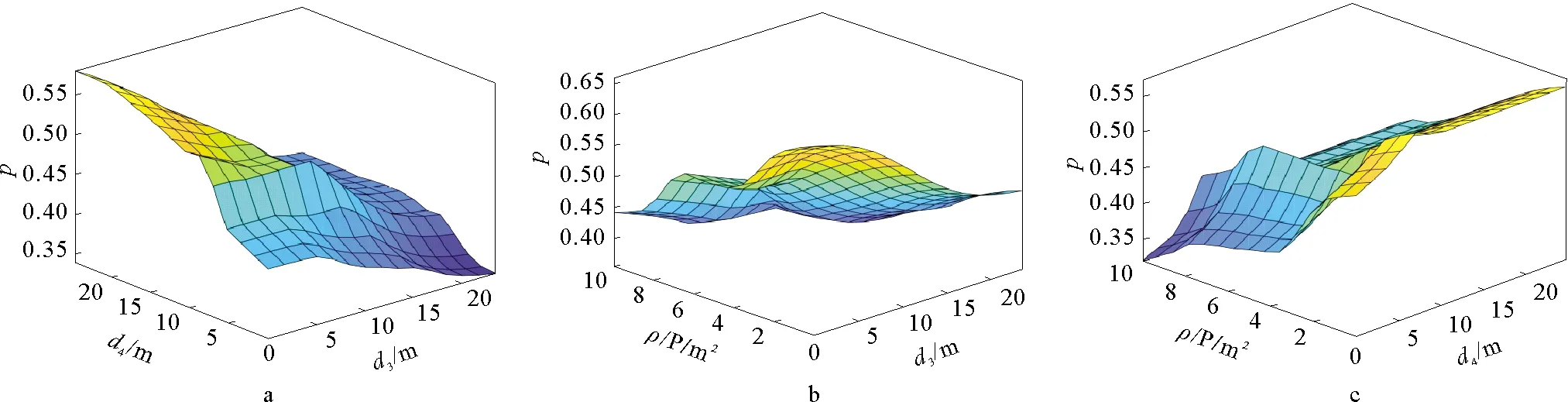
图2 模糊逻辑系统的输入变量与输出变量间的关系
(10)
基于隶属度函数,可以根据距离d3,d4和密度ρ的具体输入值来确定它们的具体状态。进而,本文采用“如果—那么”规则进行乘客车门选择的模糊推理过程。本文根据有限的调研数据结果,制定了如表1所示的乘客选择目标车门的模糊规则库。以其中规则7为例,如果乘客到某个车门的距离d3短,该车门到火源的距离d4长,且该车门周围的密度ρ小,乘客会认为这个车门更有利于快速逃生,则该乘客选择此车门的模糊概率p为高。本文采用经典的质心去模糊化方法[38],如式(11)所示,将模糊系统输出的模糊概率p转化成乘客选择某个车门的概率的精确值p*。其中X是输出变量p的模糊集合,μ(x)为p的隶属度函数。

表1 乘客选择目标车门的规则库
(11)
1.4 乘客运动优先级
在行人动力学模型研究过程中,为了完成行人的位置更新,需要规定行人运动优先级。考虑到发生突发事故时地铁车厢内乘客进行疏散的过程中会出现多名乘客竞争同一位置的现象,因此本文采用随机生成乘客运动优先级的方法。当有多名乘客竞争同一元胞位置时,在这些乘客中随机选取一名乘客移动到该元胞,其余乘客则留在原位置等待;当两名乘客同时选择对方当前的位置作为自己下一步移动的目标位置时,则彼此交换位置;当乘客移动到车门所占据的元胞位置时,在下一时间步长内,该乘客视为离开车厢;当所有乘客都离开车厢后,仿真过程结束。
本文中,地铁突发事故(以火灾为例)下车厢内乘客疏散运动的仿真流程图如图3所示。

图3 车厢内乘客疏散运动的仿真流程图
2 仿真
2.1 仿真环境
本文以如图4所示的部分地铁车厢内乘客的疏散情况为例,展开了相关的仿真模拟研究。将车厢内部区域划分为0.5 m×0.5 m的正方形元胞,用圆点代表车门,圆圈代表座椅,星号代表事故点(本文中指火源,不考虑火的扩散,火源以其中心点占据的一个元胞表示)。为了保证本文模型的有效性,在进行仿真前,需要对式(1)、(2)以及式(4)中的4个参数Ks,Kd,x1,x2进行校准。受限于真实疏散数据的难获取性以及真人
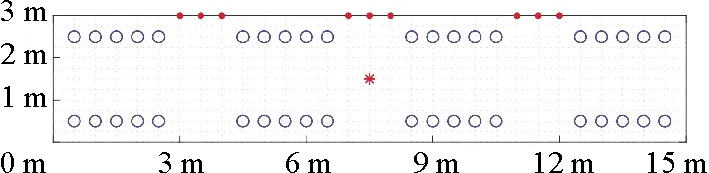
图4 仿真环境
实验的危险性,本文采取反复进行仿真模拟实验的方法[39],在保证模拟过程中乘客的运动演化规律符合现实经验的基础上,将疏散时间和通过各车门疏散的乘客比例作为参数调整的依据,同时还考虑了这些参数的选取标准,如动态场对于乘客疏散的影响不应大于静态场;乘客的速度应该与生活中实际速度相符等。最终采用误差最小的参数,取Ks=1,Kd=0.1,x1=0.9,x2=0.1。为确保数据的有效性,本文所有仿真实验均重复进行20次。
2.2 乘客运动过程
图5给出了乘客疏散过程中不同时刻的仿真快照。如图5a所示,黑色圆点代表地铁车厢中的乘客。当T=0 s时,地铁车厢中所有座椅均被坐满,其余乘客随机分布在车厢中。假定中部车厢(本文中的中部车厢是指除车头车厢和车尾车厢外的其它车厢)发生火灾,乘客需快速离开车厢到达站台。当T=3.6 s时,如图5b所示,乘客开始向车门运动,部分乘客可迅速离开车厢。当T=6.4 s时,从图5c中可以清晰地观察到发生火灾的车厢中乘客会向远离火源而距离自身较近的车门运动并通过该车门离开,同时可观察到明显的从众现象。当T=9.2 s时,如图5d所示,车厢内的大部分乘客可实现安全疏散。

图5 乘客疏散过程中不同时刻的仿真快照
2.3 火源位置对疏散时间的影响
当地铁车厢内突发火灾时,火源位置是影响乘客疏散路径选择的重要因素之一。火灾发生在不同位置,对于乘客车门选择的影响较大。当火源位于某个车厢车门附近时,该车厢内的大部分乘客将不会选择该车厢车门逃生,而是先向相邻车厢运动,然后通过相邻车厢车门逃生。这时,将会导致地铁车厢车门的利用率降低,且远离火源的相邻车厢车门拥挤程度增加,进而导致乘客的疏散时间增加,乘客整体的疏散效率降低。本文模拟了火源位置在第一节和最后一节车厢(车头和车尾)以及在中部车厢时乘客的疏散运动过程并得到了3种情况下乘客的疏散时间。
图6给出了火源位置在不同车厢时乘客的运动情况。如图6a所示,当火源位置在第一节车厢时,该车厢中大部分乘客会先向相邻的第二节车厢移动,然后通过第二节车厢车门疏散,当该车厢车门附近的拥挤程度较高时,部分乘客会继续向右侧相邻的第三节车厢移动,最后通过第三节车厢车门疏散出去。当火源位置在中部车厢时,如图6b所示,此车厢的大部分乘客首先向着相邻两侧的车厢移动,然后通过相邻两侧的车厢车门疏散。当火源位置在最后一节车厢时,如图6c所示,此时乘客的运动过程与火源位置在第一节车厢时相似。

图6 火源位置在不同车厢时乘客运动情况的仿真快照
图7a~图7c进一步给出了火源位置在不同车厢时从各个车厢车门疏散的乘客人数比例。由图7a和图7c可以看出,当火源位置在第一节或最后一节车厢时,通过第一节或最后一节车厢车门疏散的乘客数量较少,而通过中部车厢车门疏散的乘客数量较多,分别占乘客总人数的44%和48%;由图7b可以看出,当火源位置在中部车厢时,只有13%的乘客通过中部车厢车门疏散。

图7 3种情况下通过各个车门的乘客人数比例
图8给出了疏散时间与火源位置的关系。从图8中可以看出火源位置可明显影响疏散时间。当火源位置在第一节或最后一节车厢时,行人的疏散时间大致相同。当火源位置在中部车厢时,乘客的疏散时间是9.36 s,与其它两种情况相比,疏散效率提高了8.9%。这是由于当火源位置在第一节或最后一节车厢时,其中大多数乘客会向相邻的一节车厢移动,此时相邻的一节车厢的车门相当于承载了两个车厢的乘客量。因此,车门附近可能会产生拥堵,使得疏散时间增加,疏散效率降低。此外,当相邻的一节车厢车门附近拥堵程度较高时,乘客会继续向远离火灾的另一节相邻车厢移动,这同样也增加了疏散时间。而当火灾发生在中部车厢时,中部车厢的大部分乘客会向两侧相邻车厢疏散,两侧相邻车厢车门所承载的疏散压力虽有增加,但是相较上述情况要小一些,因此,疏散效率较高。
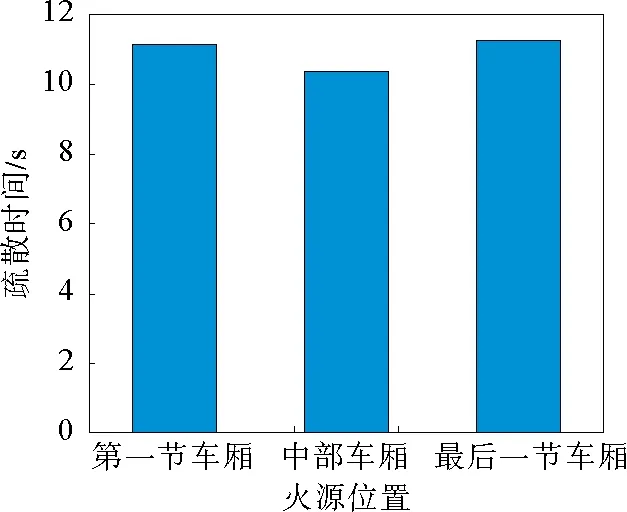
图8 疏散时间与火源位置的关系
2.4 车门有效利用宽度对疏散时间的影响
在地铁车站中,屏蔽门在保护乘客安全、稳定站内环境以及节能减排等方面发挥了巨大的作用。图9a为地铁站台屏蔽门实物图。正常情况下地铁列车进站停车时需要地铁车厢车门与屏蔽门对齐后,如图9b所示,再开启两个门,从而让乘客完成上下车行为。然而在紧急情况发生时,由于列车需要紧急停车,会出现地铁车厢车门与屏蔽门对不齐的情况,如图9c所示,这就会导致乘客下车时车厢车门的有效利用宽度发生变化,如图10所示。本文进一步模拟了地铁车厢车门的有效利用宽度为1 m和1.5 m时乘客疏散时间的变化情况。

图9 地铁站台屏蔽门与车厢车门示意图
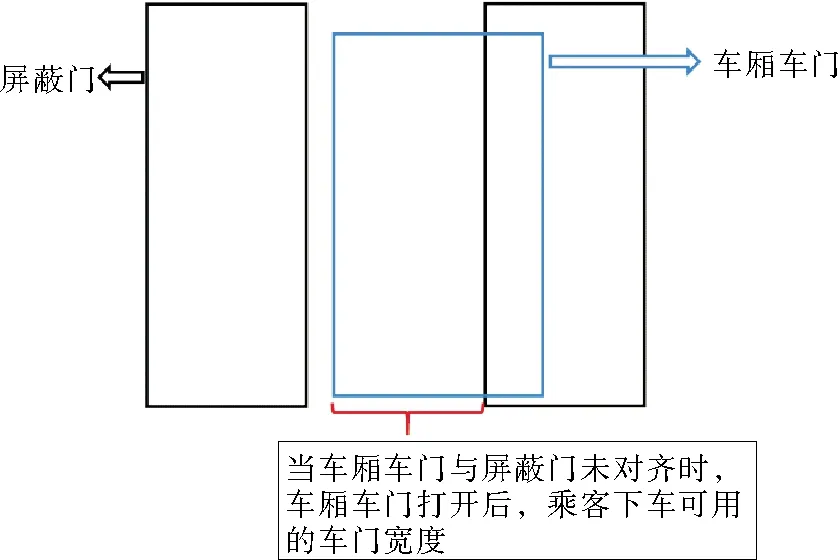
图10 两门未对齐时车厢车门有效利用宽度
图11给出了疏散时间与车门有效利用宽度的关系。如图11所示,当地铁车厢车门有效利用宽度为1 m时,乘客的疏散时间是10.48 s。当车厢车门有效利用宽度增加到1.5 m时,乘客的疏散时间为9.36 s,此时疏散效率提高了10.7%。这说明当地铁车厢内发生突发事故列车紧急停车时,地铁车厢车门与屏蔽门的对齐程度越高即增加车门的有效利用宽度,单位时间内允许通过车厢车门下车的乘客数就越多,能够有效减少乘客从车厢疏散的时间,从而有助于提高乘客的疏散效率。

图11 疏散时间与车门有效利用宽度关系
综上所述,在地铁列车运行设计过程中,要保证突发情况下地铁车厢车门尽可能与屏蔽门对齐,以提高车门的有效利用宽度,有助于提高乘客的疏散效率。
2.5 座椅排布对疏散时间的影响
当前,中国地铁车辆的座椅主要采用纵向排布的方式。除此之外,还有横向排布以及横纵交叉的排布方式。图12列举了4种不同的座椅排布方式。图12a所示的情景一为单排纵向的座椅排布方式,图12b所示的情景二为单排横向的排布方式,图12c所示的情景3为单排纵向与双排横向相结合的排布方式,图12d所示的情景4为双排横向的排布方式。与横向排布方式相比,采用纵向排布的方式载客量更大,采用横纵交叉以及双排横向的座椅排布方式虽然在一定程度上增加了坐席数量,但是其疏散通道面积相对较小,在一定程度上限制了乘客的运动。因此,不同的座椅排布方式,不仅坐席的数量不同,其疏散通道的有效利用面积也不同。本文仿真模拟了图12所示4种不同的座椅排布方式下的乘客疏散行为,得到了相应的疏散时间如图13所示。
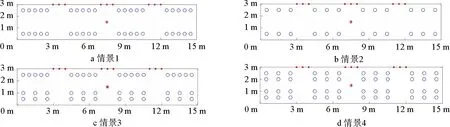
图12 地铁车厢内不同的座椅排布方式示意图
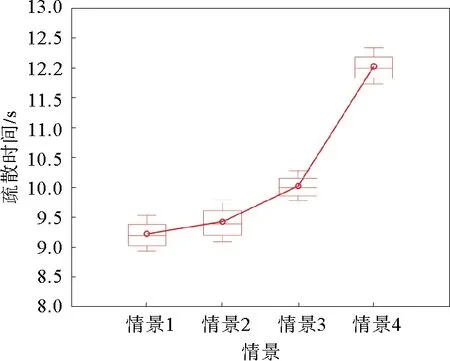
图13 疏散时间与座椅排布方式关系
如图13所示,在情景1的座椅排布方式下,乘客的疏散时间为9.36 s。在情景2的座椅排布方式下,乘客的疏散时间为9.48 s。情景2与情景1的座椅排布方式相比,疏散效率相差不大。这是因为两种排布方式下疏散通道的
有效利用面积相同,二者的主要区别在于,情景1的排布方式更能够满足乘客对于舒适度的要求(即尽可能地让更多的乘客坐在座椅上)。在情景3的座椅排布方式下,乘客疏散时间为10.12 s,与情景1的座椅排布方式相比,疏散效率降低了7.5%。在情景4的座椅排布方式下,乘客疏散时间为12.2 s。情景4与情景1的座椅排布方式相比,疏散效率降低了23.3%。此外,情景3座椅排布方式下乘客的疏散时间明显小于情景4下的疏散时间,这说明当增设多排座位时,疏散通道的有效利用面积减小,乘客离开座位的时间也会增加,从而使整体的疏散效率降低。
综上所述,采用双排横向的座椅排布方式,虽然可以满足更多乘客的舒适度要求,但却牺牲了疏散通道的有效利用面积,不利于紧急情况时地铁车厢内乘客的疏散。而采用单排纵向的座椅排布方式既有利于提高疏散效率,又能够尽量地满足乘客的舒适度要求。
3 结论
本文基于元胞自动机模型提出了突发事故下地铁车厢内乘客的疏散运动规则,并利用模糊逻辑理论来研究乘客的车门选择行为。基于所构建的模型,进一步研究了事故点(本文中指火源位置)、车门有效利用宽度以及座椅排布方式3个因素对乘客疏散的影响。通过Matlab进行仿真模拟实验并得到以下结论:当火源位置在中部车厢时的疏散效率要比火源位置在车头或车尾车厢时高8.9%;地铁车厢发生突发事故需要紧急停车时,在一定范围内增加地铁车门的有效利用宽度,有利于提高乘客的疏散效率;座椅排布方式会对乘客的疏散效率产生一定影响,常见的单排纵向的排布方式更有利于乘客在紧急情况下的疏散。本文的研究成果可为车厢内乘客的紧急快速疏散提供一定的辅助决策支持。然而,本文在研究突发火灾时地铁车厢内乘客的疏散运动时,并未考虑火源自身参数。在未来的研究中,我们将进一步丰富仿真场景,讨论火源参数在乘客疏散过程中的影响作用。

