区块链背景下的供应链牛鞭效应协调研究

张明昊，卓翔芝，石 莉

（1.淮北师范大学 经济与管理学院，安徽 淮北 235000；2.淮北师范大学 计算机科学与技术学院，安徽 淮北 235000）

0 引言

1958年，供应链设计之父Forrester［1］提出牛鞭效应的前身—弗雷斯特效应，后由Lee等［2-3］将其定义为牛鞭效应.期间，发源于麻省理工学院著名的“啤酒游戏”掀起不同行业背景的人们共同探究库存量随时间迁移发生巨变背后奥秘的热潮.1989年，Sterman 等［4］通过对啤酒游戏的仿真实验初步证实牛鞭效应的真实存在性，使得牛鞭效应成为众多从事供应链管理研究工作的学者们极力破解的重要课题之一［5］.

传统供应链信息系统中的信息孤岛现象导致信息交互的及时性及真实性难以保障［6］.牛鞭效应是需求信息传递过程中普遍存在的一种因信息不对称引发的需求变异放大现象，通常表现为供应商收到的订购量往往比买方的实际销售量呈现更大的波动，由此产生的信息扭曲和混乱在供应链下游至上游库存系统传递的过程中层级放大［7］.受牛鞭效应影响，企业在承受高库存风险带来的隐患，也面临着诸如资源浪费、高成本以及低产能利用率等一系列不利于企业生存和发展的负面问题［8］，恶性循环之下导致供应链效率低下，严重制约产业进步的空间.

由于牛鞭效应本质上是由信息不对称导致的需求预测偏差，因而对供应链引入数字化技术用于加强成员间的信息交互具有重要意义.区块链作为比特币的底层架构，起源于一个基于分布式账本的数字货币解决方案，是一种全新的数字化技术［9］.区块链实质上是一个大型的实时数据库，具有去中心化、公开透明、可溯源追踪和无法篡改等显著特征［10］，广泛应用于电子商务发展、数据权限获取、金融监管等场景.依托区块链搭建的网络分享平台能够对链上的每笔交易生成唯一的时间戳标签和对应的哈希值密码［11］，解决传统交易因信息不对称带来的信任问题，以及因证据效力不足引发的纠纷问题，对大数据时代的供应链管理具有深远意义［9］.

区块链应用背景下，在弱化牛鞭效应的同时，对供应链的主体之间的利润进行分配和协调是本文研究的重点.考虑到不同决策方案下博弈主体的地位会影响到博弈的结果，要使双方在一定程度上达成共识，占优方需对劣势方实施契约激励.成本分担与收益共享是提高供应链整体协调的两种重要契约形式［12］，相关研究表明：契约的签订不仅有助于降低双重边际化和信息不对称等不利因素所带来的影响，还能在增加单个企业利润的同时提升供应链的整体利润，实现供应链协调和竞争优势［13-15］.如徐春秋等［16］通过构建零售商和制造商微分博弈模型发现，在一定条件下，成本分担契约可以实现制造商、零售商和整个供应链系统利润的帕累托改善.冉文学等［17］对零售商和供应商引入区块链技术构建博弈模型，并利用收益共享契约对双方的利润分配进行协调，验证区块链技术的应用使整个供应链的收益得到提高，且零售商的订货量更逼近于市场真实需求，有效降低供应链库存风险.

当前，基于区块链技术展开的供应链协调和优化研究已取得一定成果［18-19］，但问题的假设普遍建立在默认零售商所产生的订单量即为市场真实需求的前提下.本文拟从问题的源头出发，假设市场的真实需求量经牛鞭效应放大，以单个零售商与单个供应商所构成的两阶段供应系统为研究对象，利用博弈论的方法求解在区块链技术和牛鞭效应二者共同的作用下的最优区块链引入程度、最优订货量以及最优生产量.在此基础上对模型引入成本分担契约，推导模型的均衡解，实现对各供应链主体利润的协调.

1 问题描述与符号定义

1948年，信息论之父Shannon［20］借助热力学相关知识提出信息熵的概念.信息熵是根据事物本身对信息的贡献度来描述信源的不确定性的度量工具.在系统S的内部，离散事件xi={x1,x2,...,xn}发生的概率Pi={P1,P2,…,Pn} 的信息熵为

Hc(S)、Hd(S)分别表示供应链中信息传递的期望熵值、非期望熵值，pi表示信息传递的通透性，熵比α［21］用以描述供应链的信息传递效率，如图1所示.

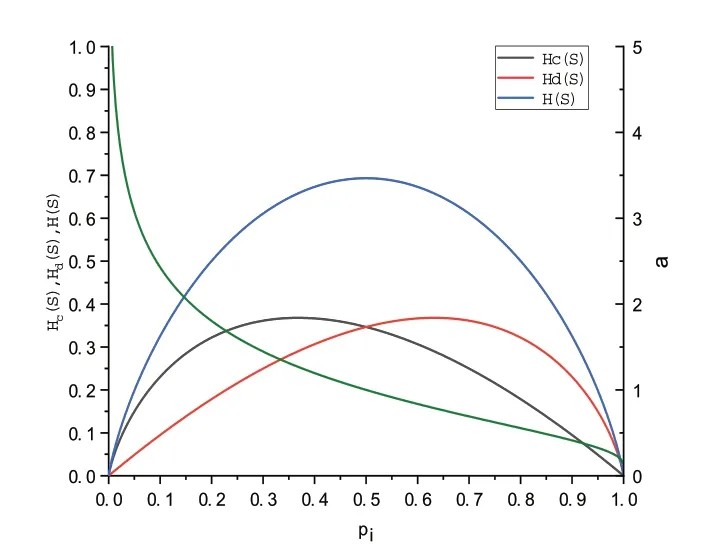
图1 信息传递规律图

由图1 知，熵比α在区间上满足(0,+∞)的分布，考虑到实际供应链管理不仅追求低熵，还追求高信息精确率，即考虑上下层级之间的信息通透性不小于0.5，熵比α∈(0,1].由于牛鞭效应源于供应链上主体的信息不对称性，故本文将牛鞭效应δ定义为关于信息传递效率的函数

区块链技术要求供应链中的相关节点供应商信息“上链”实现共享，通过信息集成的方式整合交易信息，进而形成公开透明的分布式账本受社会各界监督.对经典的香侬通信模型引入区块链技术，改进后的通信模型如图2所示.

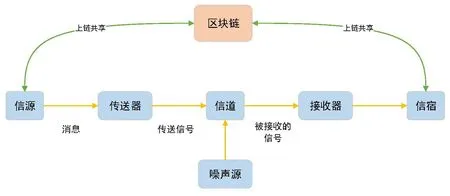
图2 改进的香侬通信模型

本文涉及的符号及定义如表1所示.设市场的原始需求为x，经牛鞭效应放大后的市场需求为y；x为连续随机变量，其概率密度函数为f(x)，分布函数F(x)连续可微，x∈[0，+∞)；零售商向供应商的订货量为D，供应商的生产量为Q；零售商以价格pr向顾客出售产品，边际成本为cr；供应商的批发价格为ps，边际成本为cs；区块链技术的应用程度为ω，引入区块链技术的成本为；期末未出售商品的单位残值为v；基于杨礼凡［22］所构造的牛鞭效应传导函数，对区块链应用程度添加弹性系数β，得到

表1 符号及定义

设零售商用r表示，供应商用s表示；市场真实需求量经牛鞭效应放大后，零售商与供应商的期望收入和对应的期望利润如下.

零售商的期望收入E(Rr)和供应商的期望收入E(Rs)

令t=(1-βω2)δ，

零售商的期望利润E(πr)和供应商的期望利润E(πs)

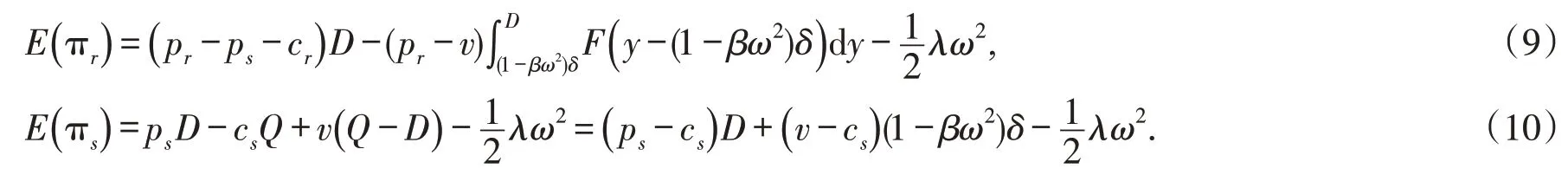
2 模型构建

2.1 分散决策情形下的通用模型

零售商根据利润最大化原则确定最优订单数量，有

将D1代入期望利润表达式，取得零售商的实际期望利润

再根据零售商的实际期望利润确定区块链应用程度，实际期望利润关于区块链应用程度的一阶和二阶导数为

联立式（12）与式（15），可得

由式（16）可知，牛鞭效应δ随着其内部信息熵比α的增大而增大（δ=ekα），由于反函数与原函数同增同减，故随着信息熵比α的增大，区块链技术的应用程度增大，与模型假设相符.

将D1代入式（14），有，即ω1为最大的区块链应用程度.由于引入区块链技术会一定程度上的削弱需求波动，即条件1满足ω≠0 时的订货量必然小于ω=0 的订货量，必有

与零售商所面对的随即市场不同，供应商面对的是固定需求的零售商市场.供应商的生产发生在零售商订货后，当ω≠0 时，供应商的生产量为

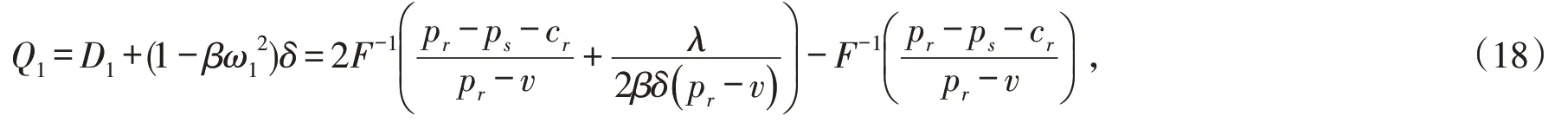
此时，供应商的期望利润关于区块链应用程度的一阶和二阶导数为：

式（19）无法直接取得供应商区块链技术应用程度的最值，需联系实际情况进行分析.根据供应商的期望利润公式，只要零售商大数额的订货量产生的利润能够超过生产成本，供应商反而希望牛鞭效应尽可能的大，尤其是当产品的残值较大时，牛鞭效应的增大不仅没有产生损失，甚至会带给供应商更大的利润空间；而当过量生产带来的经济损失较大，特别是当产品的残值也较小时，牛鞭效应的增大会进一步加剧过量生产所造成的经济损失，供应商倾向于通过提高区块链技术的应用程度来平衡收益，且在引入成本较低的前提下应用程度越大越好，故有

针对零售商与供应商的最优区块链技术的应用程度不同的状况，默认与期望应用程度较低的一方保持一致.从而，当前供应链的最优区块链技术应用程度为

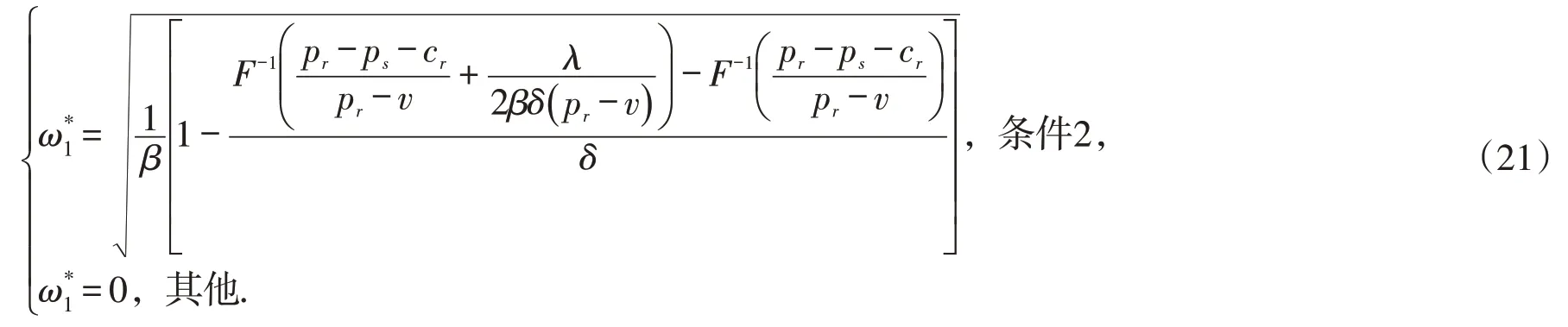
由于引入区块链技术会一定程度上削弱需求波动，条件2应满足

同理，零售商的最优订货量，供应商的最优生产量为

此时零售商和供应商各自的期望利润为

由上文的分析过程知，零售商与供应商对于区块链的应用程度的理想化目标是互异的，此时供应链中选取同等区块链应用程度是建立在双方各自做出让步的前提下，即双方都未达到自身的最优区块链应用程度.因此，为提升供应链绩效，需对模型引入契约进行协调.

零售商根据利润最大化原则确定最优订单数量，有

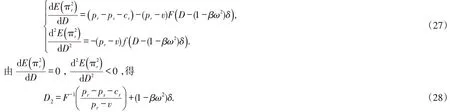
将D2代入期望利润表达式，取得零售商的实际期望利润为

再根据零售商的实际期望利润确定区块链应用程度，实际期望利润关于区块链应用程度的一阶和二阶导数为

联立式（28）与式（31），可得：

由于供应商希望区块链的应用程度达到100%，从而协调后的区块链应用程度仍由零售商决定，则供应商的生产量为

引入成本分摊契约后供应商的期望利润为

零售商根据利润最大化原则确定最优订单数量，有：

将D3代入期望利润表达式，取得零售商的实际期望利润为

再根据零售商的实际期望利润确定区块链应用程度，实际期望利润关于区块链应用程度的一阶和二阶导数为

联立式（39）与式（42），可得

由于供应商希望的区块链的应用程度为零，从而协调后的区块链应用程度仍由供应商决定.该情形下，供应商的期望利润为

其中，供应商的生产量为

2.2 集中决策情形下的通用模型

集中决策能够在提升供应链绩效的同时增强风险的抵御能力，该情形下，零售商和供应商无需根据自身利益最大化标准来进行决策，此时的决策者以全局最优为出发点［23］，供应商制定的批发价格ps将作为内部转移载体被消去，影响供应链的总利润的参数为：产品零售价pr、零售商的边际成本为cr、供应商的边际成本为cs，以及区块链技术的应用程度ω.

将式（8）与式（10）相加，得到供应链的总期望利润表达式

与分散决策时的步骤类似，根据供应链利润最大化原则确定最优订单数量，有

将D4代入期望利润表达式，取得供应链的实际期望利润为

再根据供应链的实际期望利润确定区块链应用程度，实际期望利润关于区块链应用程度的一阶和二阶导数为

联立式（54）与式（57），可得

供应商的生产发生在零售商订货后，由Q4=D4+(1-βω42)δ得，供应商的生产量为

此时，供应链的期望利润为

在实际生产经营活动中主体双方进行集中决策的案例是相对较少的，主要原因在于，在集中决策情形下，针对某个问题主体之间虽达成相同的决策意见，但最终的收益分成比例由主导方制定（通过调整内部转移载体批发价格），即当一方占据主导地位时，选择跟随的一方将获得保留利润；当双方均不能主导供应链时，收益分成比例将取决于双方的议价水平.

3 结论

针对供应链上下游主体之间因信息不对称所引发的牛鞭效应现象，本文构造单供需环节牛鞭效应传递模型，探究区块链技术应用程度对于牛鞭效应的抑制作用.研究发现，区块链技术的应用程度ω与信息传递的通透性pi呈反比，与信息熵比α呈正比；随着牛鞭效应的增大，区块链技术的应用程度相应提高，该结论与实际情况能够很好的吻合；此外，区块链技术的引入能够降低零售商的订货量和供应商的生产量，一定程度上弱化供应链的需求波动.由于供应链中主体理想的区块链应用程度存在差异，引入成本分担契约能够使主体双方的区块链应用程度得到协调的同时提升供应链的总利润，虽然获利更多的一方往往是主导方，但跟随的一方至少也能获得保留收益.本文存在一些局限性，信息传递通透性的大小取决于评价主体的判断，易受人为主观因素的干扰，后续可建立科学合理的指标评价体系，更好的为刻画牛鞭效应服务.此外，由于现实中成本分摊的比例不完全由主导方所掌控，博弈主体的谈判能力同样起到重要作用，因此，研究结论与真实状况存在一定误差，未来将对模型做进一步的优化.