一对多交互式在线客户服务排队模型

戴 韬,赵 星

(东华大学 旭日工商管理学院,上海 200051)

随着移动互联网技术和社会化媒体的发展,人们悄然改变的沟通习惯已经影响到客服中心,语音热线来话量逐步下降成为普遍趋势,企业和客户之间的联系不再是以电话交流为主的方式,客户通过微信、QQ、阿里旺旺等移动即时通讯软件以在线聊天的方式与企业交流、沟通。相应地,企业传统的电话呼叫中心升级为以在线沟通为主要渠道的在线客户服务中心。

从客户角度,在线客服中心能照顾更多客户感受：“反应慢”的客户有了足够的思考时间,腼腆的客户有了独立的提问环境；截屏、语音、文字等沟通方式更多样,能更快地解决问题；可以根据自身的情形控制沟通的节奏,忙时不用立刻回复；满足了新生代用户不喜欢语音交流的紧迫感和某些场合的隐私性要求。从企业角度,在线客服中心提供了更多的便利：效率高、节约人力资源,一名客服人员可以同时服务多名客户,平均每位坐席可以接待5～15名客户；在线客服系统可为客户生动地提供服务选项,给足客户思考时间,更准确地了解客户需求,从而做到准确分流,让服务更细分化；基于移动互联网的在线客服对硬件及坐席的环境要求较低,可以更加容易地吸引兼职人员进行远程服务,为自由从业客服和云客服的发展提供了可能。

以排队论的观点,在线客服中心与传统电话客服中心的关键区别是客服与顾客间的交互模式发生了根本性改变：一个在线客服可同时为多个顾客提供服务(简称“一对多”),而在电话客服中心,一个客服同时仅能为一个客户提供服务(简称“一对一”),如图1所示。

图1 两种服务模式对比

与传统客服中心一样,顾客的服务满意度与员工的工作满意度都影响着企业的服务拓展与运营绩效[1],因此,运营经理需要平衡顾客服务水平(一般用顾客的平均等待时间来衡量)与运营成本(员工的繁忙程度)之间的矛盾,将客户需求量转化为客服人员需求量是在线客服中心运营的关键步骤。基本的排队论公式是在“一对一”服务模式下推导得出的,无法直接用于在线客服“一对多”的服务模式,故本文分析“一对多”服务模式的排队特点,提出描述排队状况的性能指标,并建立相应的双层排队模型来计算指标,为在线客服的运营管理提供理论支撑。

1 文献综述

在传统的客服人力资源配置研究中,各种排队模型已经被广泛研究,其基本思路是将顾客到达视为泊松流,各个时段相互独立且客服服务时间服从负指数分布,Green等[2]将该方法称为SIPP方法。在SIPP方法假设下,可以采用基于M/M/N的Erlang-C公式计算在满足一定服务水平下所需的客服人数。吴佳骥等[3]在求解多技能呼叫中心人力需求时,利用经典的Erlang-C 模型求出各技能在各个时段的人力需求。虽然Erlang-C公式是目前在客服中心中应用最广泛的,但大量的文献也提到该模型存在的诸多局限性,如顾客不愿意等待而离开,不同时段之间有相关性等。Yom-Tov等[4]分析了顾客重复进入系统的Erlang-R模型。Jouini等[5]对有等待信息告知、多等级顾客以及顾客耐心有限的服务排队过程构建了相应的模型,并提出了基于马尔科夫链的预计等待时间的估计方法。于淼等[6]研究了带有排队信息提示的M/M/N+M排队模型,给出了稳态系统下的性能指标计算公式,并设计了基于二分法和固定点法的求解方法。

综合现有研究不难发现,经典的Erlang-C 模型以及相关的衍生排队模型都基于客服与顾客间“一对一”的交互模式。在线客服与顾客“一对多”的交互模式下,单个顾客在得到客服的一次回复后可能继续留在系统并发出下一条咨询,每个客服在回复完一条咨询后会继续回复其他顾客的咨询。因此,在“一对多”的交互模式下的排队问题不再是标准的排队问题,也无法使用现有“一对一”模式下的排队模型。目前,在线客服的相关研究主要集中于服务模式及服务质量的定性分析：万君等[7]对电子商务网站在线客服弹出窗口对用户行为的干扰问题做了实证分析；刘顺忠[8]利用实证分析研究了网络购物中顾客购买意向受在线客服沟通方式和商品特征的影响机制。

国内有少量研究将排队论和在线客服相结合：江小云[9]为了确定合理的客服数量将M/M/C/∞/∞排队理论应用于网络实时沟通服务系统；吴贤佑[10]在对某在线客服系统优化时将M/M/C/∞排队模型应用到系统中来求解系统的性能指标。但这种不考虑客服与顾客“一对多”的交互模式而直接简化为标准的排队模型,导致计算出的服务水平和真实的服务水平存在较大差距,严重影响最终客服排班结果的准确性,本文3.2节仿真结果也证明了这一点。还有学者对在线客服的新特点下的运营问题展开了研究：Luo等[13]研究了不考虑顾客的不耐烦性,如何配置最优数量的在线客服人员数量；Tezcan等[14]在Luo等的基础上进行了研究,将模型成果扩展到存在不耐烦顾客的场景。与本文相比,这两篇文章的重点是在线客服的人员数量配置,为了实现其研究目的,两篇文章都将其中的基础因素——单个坐席对不同数量顾客的服务速度作为已知参数。然而,现实中的客服中心仅能够已知客服回复单条消息的速度,其表现出的服务速率是跟客服与顾客的回复速度及顾客数量等有关的函数,而关于这个函数的具体解析式,这两篇论文均未讨论。Legros等[15]也研究了在线客服的运营问题,其主要关注点是当坐席人员数量确定时,如何在不同坐席之间进行客户需求的分配。与本文最为相近的是Campello等[16]的研究,他们将医疗服务、在线客服与社区咨询等排队问题均抽象为基于“Case Manager”的排队模型,并提出了主要排队指标的解析公式,本文与其最大不同是排队对长与排队时间的计算逻辑,具体比较详见3.3节。

综上所述,比起大量的“一对一”排队的研究,“一对多”排队模式下的研究较少,少数的研究也因为关注点的不同,对于最基础的单客服排队模型反而缺少深入研究。因此,本文根据现实有可能直接获取的参数作为已知参数,并提出该模式下的关键排队指标,通过建立双层排队模型推导关键指标的解析公式。最后,通过与仿真结果的对比验证解析公式的准确性。

2 排队模型及解析公式

本文研究一个客服人员服务多个顾客的基础模型,实际中N个客服的问题既可以近似地将顾客平均分配给各个客服,变成N个互相独立的“一对多”基础模型,也可以在本文的基础模型上,考虑不同的负载之上的客服服务速率,实现最优的人员配置与负载分配[13-15]。因此,单服务台的“一对多”排队模型是在线客服的运营优化的基础模型。

2.1 符号设定

参考文献中对顾客到达时间和客服服务时间分布的研究[11-12],以及总结了天猫平台上多个店铺使用旺旺工具对顾客提供服务的实际场景。对在线客服服务过程的相关参数做出如下假设：

(1)顾客到达是一个参数为λ的泊松过程,其间隔时间服从均值为1/λ的指数分布。

(2)顾客发出每条咨询消息所需时间服从均值为θ的指数分布。

(3)客服回复顾客每条消息所需时间服从均值为μ的指数分布。

(4)考虑到客服回复压力以及回复质量,客服最大同时接待的人数为k,系统中的顾客总数超过k人后,顾客进入一个容量无限的空间进行排队,并根据FCFS的原则,如果一旦有一个顾客完成服务,队列中排在最前面的顾客进入到服务队列中与其他k-1个顾客同时接受客服服务。

(5)顾客咨询i条的概率为p(i),则顾客平均咨询条数的期望为：E[I]=∑ip(i)=A。极端情况,如果系统中只有1个顾客,客服进行“一对一”服务,则平均总服务时间为

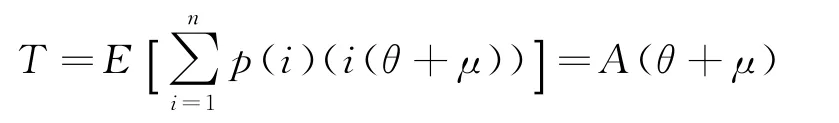
(6)顾客与客服之间是严格的“一来一往”交互过程,即一方只有收到对方的应答消息后才会继续回复。

(7)顾客喜欢在线客服的原因之一是其没有电话客服中的紧迫感,能够在处理其他事务的同时进行相关咨询,所以大部分顾客对在线客服的回复速率有较为宽容的期待,即顾客的耐心指数较高。为了简化问题,关注其他重要因素,假设顾客能在系统中耐心等待,不考虑顾客的中途放弃。这是符合顾客到达率较小的实际情况的,而对于顾客到达率较大的情况,将其作为系统的平稳条件进行考虑。

上述(2)、(3)和(5)的设定是本文与文献[13-14]的最大不同。因为根据本文对实际在线客服中心的调研分析,现实中能直接获得的与服务速率相关的参数仅仅是客服回复单条消息的时间分布,最后表现出的客服服务速率(单位时间服务的顾客人数)跟顾客的单条消息回复速度及顾客与客服之间的交互次数、当时的顾客数量等因素有关,所以不能简单地给出不同顾客数量下客服的服务速率,否则既掩盖了一些关键的变动性质,在实际应用中也是比较难测定的。

2.2 模型构建

在线客服工作时,顾客通过发送文字消息的方式跟客服人员进行沟通,顾客需要一定的时间来输入消息(服从均值为θ的指数分布),顾客等待发生在两个阶段：①刚刚到达时等待被接入到合适的客服；②在与客服沟通的交互过程中,顾客发出了消息等待客服回复。顾客通过在整个服务过程中等待时间的长短,衡量本次服务在响应性维度上的满意度。因此,传统的排队模型中的排队队长和等待时间两个指标不足以描述在线客服的排队状况,而本文则以完成整个咨询服务的时间和顾客发出消息后收到客服的平均等待时间来评价系统的绩效。

虽然从表面上看,一个客服可以服务多个顾客,但在任何一个时间点上,每个客服只能回复一个顾客的消息(类似于操作系统中CPU 服务各个进程的并发运行),因此,顾客已发出的待回复消息可以抽象为等待的“一对一”单服务台排队队列,每一位顾客只会在其所有问题咨询完后再离开。根据此特点,将在线客服的排队模型分为消息层模型和顾客层模型,双层模型的逻辑图如图2所示。

图2 在线客服双层排队模型逻辑图

其中,消息层模型是确定客服在同时接待m个顾客时,即没有新顾客到达和离开的假定下,顾客的每条咨询在得到客服的回复之前的平均等待时间,进而确定在客服同时接待m个顾客时,顾客在系统的平均逗留时间。顾客平均逗留时间将用作顾客层模型的服务速率的计算,同时在顾客层模型考虑客服的最大同时接待能力,最终推导出“一对多”交互模式下排队模型的相关性能指标。本文提出的双层模型的最大优点是将一个“一对多”的排队问题拆分为两个层次上的排队问题,而这两个层次上的排队都是“一对一”模式的,这样就可以用典型的生灭过程来描述其状态变化过程,较容易进行排队公式的推导。

2.3 消息层排队模型

因为系统中有m个顾客,所以等待客服回复的消息条数为0～m条之间,假定某时刻系统有i条消息待客服回复,则剩余m-i个顾客发出消息的速率为(m-i)/θ,此时的系统可近似为单服务台顾客源有限的排队模型[17],记为M/M/1/m/m,其稳态系统的状态转移图如图3所示。

图3 消息层模型状态转移图

图3中的状态p(i)表示消息队列中有i条消息待回复的概率,根据状态转移图可以列出如下K氏方程：

令c为系统中总的平均待客服回复的消息条数,则还未发出消息的顾客为m-c人,记新消息的到达速率为有效到达率,即

系统中等待客服回复的平均咨询条数为

结合式(3)可得

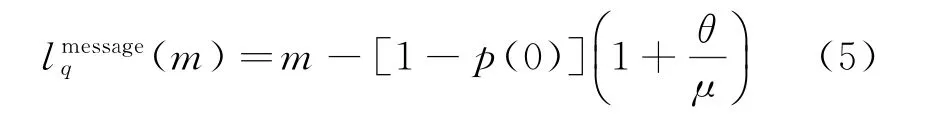
因此,根据Little’s Law,可以得到当系统中有m个顾客时,顾客每条咨询被回复需要的平均等待时间为

将式(5)代入式(6),得

根据式(7),可以得到如果系统一直平稳地保证刚好有m个顾客,每个顾客在系统中平均逗留时间为

2.4 顾客层排队模型

2.3 节中顾客的平均服务时间T(m)是在系统中刚好有m个顾客的假设下得到的,从整个客服接待过程看,客服接待的人数会随着新顾客到达和顾客接受完服务离开系统而不断变化,故需将2.3节得到的消息层平均服务时间T(m)引入到第2层排队网络中,继续考虑顾客人数不断变化的顾客层排队模型。

考虑最一般化的在线客服系统,假定该系统的最大容量为n,客服最大同时可接待人数为k,顾客到达系统的到达率为λ。当系统中顾客人数m＜k时,客服服务速率为m/T(m)；当m＞k时,剩余部分顾客耐心等待,系统的服务速率为各阶段状态转移图如图4所示。

图4 顾客层状态转移图

图4描述的是顾客无限到达的变服务速率的排队过程,为了方便求出各个状态的概率pp(i),进而求出总的服务时间,将k～n状态视为子过程1,该过程的各状态下,客服均全负荷工作,服务速率保持不变,各个状态的概率分别为pp′(k)…pp′(n),根据图4列出子过程1的k氏方程如下：

结合全过程的正则性条件：

以及全过程中k-1～k状态的状态转移方程

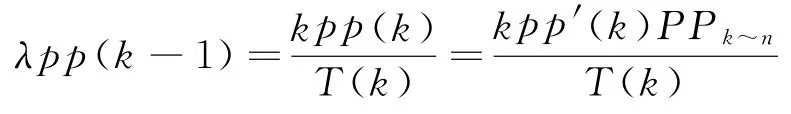
因此可求得

式中,

全过程各状态概率为当i≥k时：

当i＜k时,

可得到在系统顾客人数不断变动的情况下,顾客平均逗留时间为

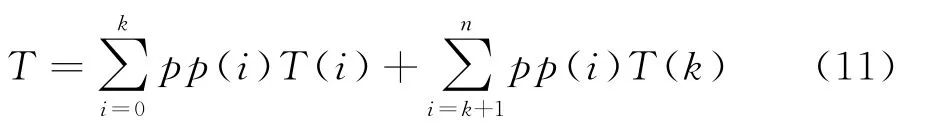
系统中平均顾客人数即系统平均队长为

系统中顾客平均等待回复时间为

由此,可通过双层模型得到3个关键指标,即系统平均逗留时间、系统中平均客户数量和每条消息平均等待回复时间的解析公式(见式(11)～(13)),其中状态概率pp(i)由n个独立的方程组确定。在实际使用过程中,仅需给出已知参数A、μ、θ、λ、n和k,就可使用常用求解软件得到关键的排队指标。

因此,在应用模型时,可以将n→∞当作排队容量有限的特殊情况(事实上,所有的客服中心排队容量都是有限的),选择一个较大的n值进行近似即可。如在第3节算例中的情形,当选择n=20时,在最大稳态保证的到达率下,

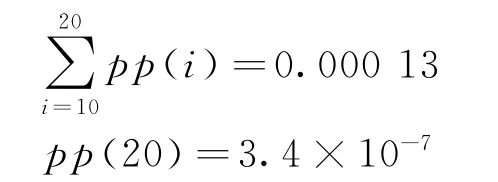
即对于n＞20的概率,完全可以忽略不计。

3 数值仿真

本仿真算例的数值来自2016年天猫商城某服装品牌的旺旺客服数据,本文统计了其16个客服2天的实际数据,得到如下已知参数：顾客发出每条消息所需时间服从θ=50 s的指数分布,客服回复每条消息所需时间服从μ=35 s的指数分布,客服最大接待顾客人数k=10人,系统能接受的顾客总数不限,根据第2节最后的讨论,用n=20进行近似,顾客的咨询条数数学期望A=3.09条。

算例中的方程求解使用Lingo软件进行,仿真结果通过使用同样的输入数据在Flexsim 软件中建模得到。

3.1 稳态接待能力分析

为了确保系统处于稳态状态,即在顾客层需要保证q＜1,即λ＜k/T(k),因此可得不同k值(单客服最大服务人数)下,系统能够接受的最大到达率。

在本算例中,当A、θ和μ这3个参数已知时,k/T(k)即系统能接受的最大到达率,得到最大可接受到达率与最大服务人数之间的关系如图5所示。

由图5可知,根据现实的管理要求,该客服中心的单人同时最大的接待人数取k=10,可以得到最大到达率λ=0.009 239 312 人/s,即为了维持稳态系统,需要保证分配给每个客服的顾客到达的平均时间间隔最小为108.2 332 s。

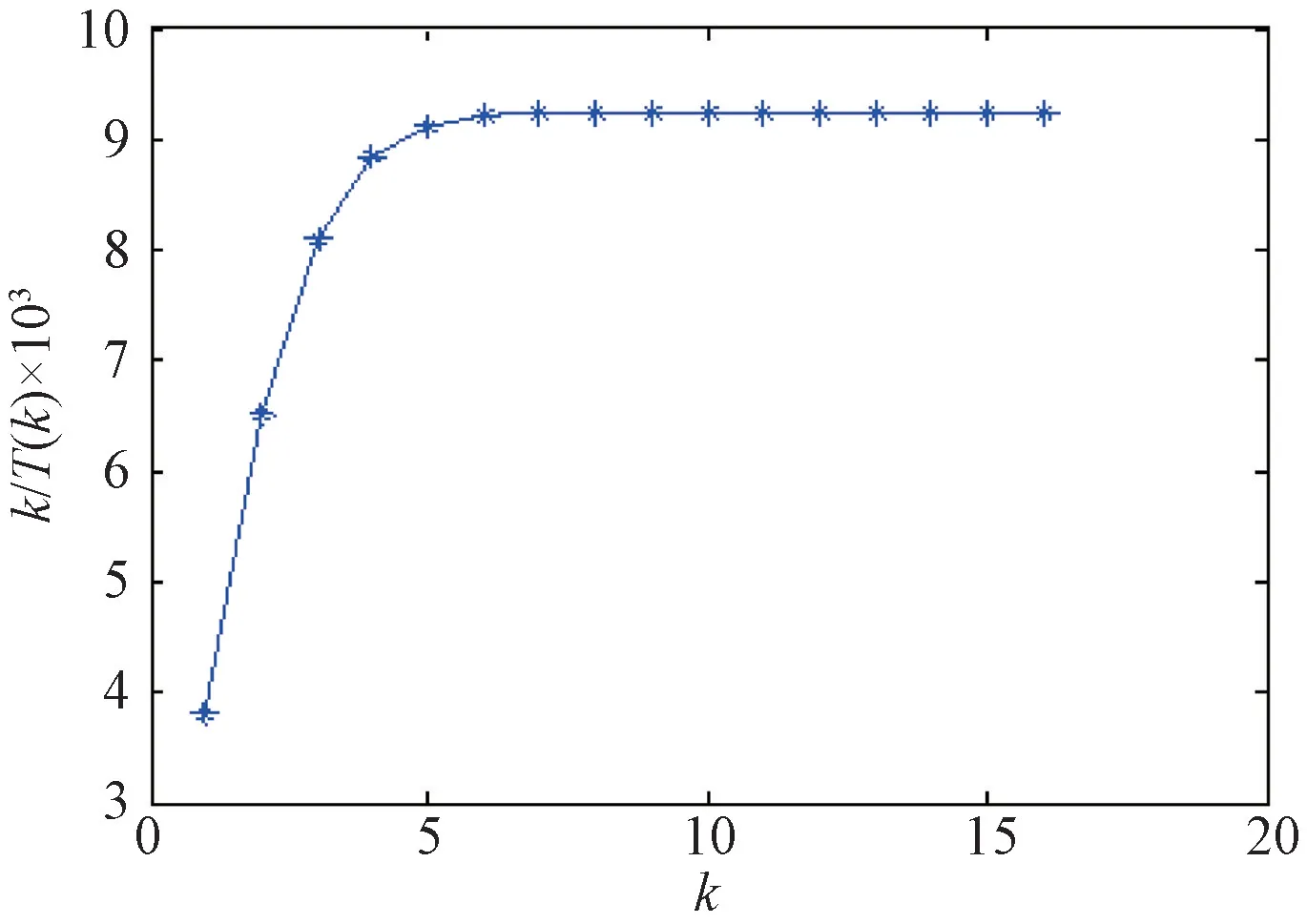
图5 最大可接受到达率分析

3.2 数值结果对比

为了验证解析模型的准确性,保证基本运营参数不变,调整顾客到达率λ得到一系列解析公式值和仿真值。其中,顾客到达率的变化区间为[0.004 167,0.01](人/s),即顾客到达平均时间间隔为[100,240](s)。

分别计算第2节提出的3个关键排队指标：平均服务时间、每条消息平均等待回复时间和系统平均客户数量,数值对比如图6所示。

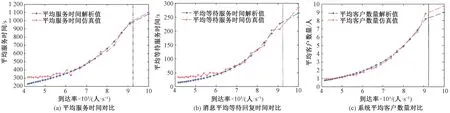
图6 关键排队指标数值对比图

分析图6的结果,当到达率较小时,图中的虚线左侧部分,解析公式值与仿真值均有较好的贴合,其中的误差是因为解析值仅能给出一个均值,而仿真结果由于是根据参数随机产生驱动事件,其值会在解析值的上下波动,说明本文构建的双层排队模型能仅利用“客服回复消息时间”“顾客回复消息时间”及“顾客的平均交互次数”这3个输入参数,很好地计算平均服务时间、每条消息平均等待回复时间和系统平均客户数这3个关键指标,并且解析过程的计算时间远远小于仿真模型的时间。

算例中的仿真时长设为28 800 s,表示一天中的8 个小时,进行10 次仿真后求平均值得到。Flexsim 软件的基本运行机理是：根据到达率随机生成顾客,每个顾客独立在仿真模型中停留,最后统计得到该到达率下排队系统的关键指标。由于Flexsim 软件的仿真特性,每次仿真均产生了数目庞大的独立顾客,使得最后统计值的变动方差比较小,并且,随着到达率变大,每次仿真产生的独立顾客数量越多,变动方差更是降低,故仿真值具有“较窄”的置信空间。表1所示为以平均服务时间指标为例,给出了几个典型到达率下的仿真置信空间。

表1 部分典型到达率下平均服务时间仿真值置信区间

解析值与仿真值的主要差距出现在到达率不断变大的过程中,在图6中为虚线的右侧部分。虚线表示到达率0.009 2个/s,即在给定参数下的系统最大可接受到达率,说明本文提出的模型仅适合应用于稳态系统,当系统处于不稳定状态(即顾客排队会无限增长),解析公式的解会急剧恶化。造成该现象的原因是,本文模型在推导中未考虑顾客的不耐烦性,而在现实的排队过程中,如果因为过高的到达率使得顾客陷入长时间的等待,理性的顾客会选择中途退出,或者在排队初期就不会进入咨询队列。

3.3 与其他近似模型对比

对于本文关注的在线客服的特别问题,部分学者曾提出可以将“一对多”交互式服务近似为N可变的M/M/N多服务台排队模型[10]。本文比较其近似方法与本文模型的效果。

将近似模型的服务速率设置为1/A(μ+θ),考虑不同的顾客到达率下,选取不同的近似服务台数,计算出相应的平均服务时间,并与本文得到的双层排队模型解析解和仿真解进行对比,如图7所示。

图7 与M/M/N 排队模型对比

通过对比发现,随着N的增加,平均服务时间逐渐趋于定值,但无论N取哪个值,平均总服务时间与仿真模型的结果始终有较大的偏差；而本文提出的双层模型却能一直与仿真值较好地贴合,表明利用近似M/M/N模型无法较准确近似“一对多”交互式排队模型。

Campello模型[16]是与本文最为相近的一个研究,该文提出了多客服“一对多”服务的排队指标近似模型,根据客户需求在多客服之间的不同分配原则,提出了T、R、B和P等4个模型,但其研究思路与本文是不同的,他们分别用近似模型计算了开始服务后每一次交互的等待时间(等待消息长度)和客服首次响应前平均等待时间(等待队伍长度)。

在单客服场景下,Campello等[16]提出的4个模型是完全一致的,其用单服务台K个有限顾客的排队近似与客户之间的交互过程,用客服满负荷工作速率乘以繁忙程度近似客服实际工作速率,为了获取繁忙程度的指标,其必须将平均消息条数(No.of visits to server,1/γ)作为已知参数。而本文的思路是,参数1/γ在现实中很难获取,故可直接将客服与顾客交互过程(消息层排队)得到的服务速率直接代入顾客层排队模型进行计算。本文模型与Campello模型在单客服下的结果比较如表2所示,表2中仿真均值的获得过程与前文一致,其置信区间同表1。

表2 单客服场景下与Campello模型对比结果

通过分析发现,在单客服场景下,虽然Campello模型能分别计算客服首次响应前等待时间和客服首次响应后等待时间,但是由于其做了2次近似,本文模型在平均服务时间指标上的计算准确度上有更大的优势。

将本文模型在多客服场景下拓展。现实中常以JSC(Join-the-Smallest-Caseload)策略进行多客服之间的工作量分配。JSC策略将新到达的客户分配给目前工作负荷最轻的客服,以保证每个客服工作量尽量平均,即在同一时刻,最繁忙与最空闲客服的顾客差1人。本文以完全平均的方式近似JSC 策略,即假设顾客完全平均分配在多个客服中。使用Campello等[16]Table 2给出的数据,用本文模型进行计算并与Campello模型进行对比。由于对参数定义的不同,将Campello数据转化为本文的数据：

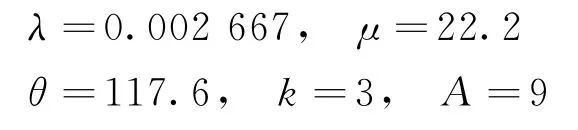
其中,本文模型不需要参数1/γ。对比结果如表3所示。

根据表3,发现本文模型无法单独计算预分配等待时间和服务中等待时间,而是直接得到了总等待时间。与Campello模型[16]一样,本文模型的结果也比仿真结果略偏小,本文模型在多客服场景上利用JSC 策略的扩展更接近于Campello 的B 模型,在多客服场景下表现不如Campello模型的原因是,本文假设每个客服的工作量、客户数量等指标是完全一致的,这在JSC 策略下由于服务速率的不确定性影响,是不可能达到的。因此,如果为了提高本模型扩展到多客服场景下的准确性,需要在路由分配时对每个客服进行独立计算并汇总。

表3 多客服场景下与Campello模型对比结果

4 结语

本文在对我国在线客服中心实际情况进行抽象假设的基础上,提出了在线客服中心排队系统的3个关键排队指标：平均服务时间、消息回复等待时间和系统平均顾客人数,并通过构建两层排队模型,将“一对多”服务模式下的排队问题变成两个层次上的“一对一”排队问题,通过生灭过程分析推导了3个关键指标的解析公式,同时给出了系统处于稳定状态的条件。通过将解析值与仿真值及M/M/N 近似模型进行对比,验证了解析公式的准确性。将本文模型与Campello 模型[16]对比发现,虽然Campello模型能应用于多客服的排队绩效计算,并且其模型能分别给出进入服务前等待时间与开始服务后的系统逗留时间,但是在单客服的场景下,本文模型得到的平均服务时间指标更加准确,且无需已知平均消息条数。而在多客服的场景下,本文模型的简单扩展不如Campello模型准确。因此,在以本文模型为基础进行多客服场景的扩展时,需要独立计算每个客服的排队指标再进行汇总,本文模型对于更加准确地计算在线客服中心的排队绩效是有理论与实际意义的。