基于双重局部保持的不完整多视角嵌入学习方法
刘彦雯,张金鑫,张宏杰,经 玲
(1.中国农业大学 理学院,北京 100083;2.中国农业大学 信息与电气工程学院,北京 100083)
0 概述
多视角数据是指对于同一个物体,从不同层面观察或从多个源头得到的特征数据[1-2]。多视角数据从不同的角度对同一物体进行描述,比单视角数据更加全面[3-4]。多视角学习[5-7]是根据各个视角间的内在联系及每个视角具有的独特属性对多视角数据进行处理和分析,进而合理充分地利用多视角数据的一种全新的学习方法。多视角学习已经成为机器学习和数据挖掘领域中备受关注的热点问题[8-10]。
随着科学技术的高速发展,人们收集和处理数据的手段越来越多种多样,在信息爆炸式增长的同时也同样面临着数据维度高和高冗余的问题,增加了实验的计算复杂度并引起维数灾难[11-12]。降维是克服维数灾难,获取数据本质特征的一个重要途径,根据是否基于样本标签信息,可以分为无监督降维和有监督降维。目前最主流的无监督降维方法有主成分分 析(PCA)[13]、Laplacian 特征映射(LE)[14]和t-分布随机近邻嵌入(t-SNE)[15]3 种。对于有监督降维,最经典的方法是线性判别分析(LDA)[16]。近年来,多视角降维方法备受关注[17-19],然而由于数据收集的困难性、高额成本或设备故障等,高质量无缺失的多视角数据很少会出现在真实的应用中,人们收集的多视角数据常常包含不完整视角[20-21]。所谓不完整视角是指在该视角下某一样本的部分或全部特征缺失。例如,在对阿兹海默症患者的诊断中,由于脑脊液的获取会对病人产生某种不利影响或攻击性,有些病人会拒绝这项检查,这就导致了该病人脑脊液这一诊断数据的缺失。当处理不完整多视角数据时,传统的多视角降维方法不能实现其良好的性能[22-23]。因此,不完整多视角数据降维方法的研究已经成为多视角学习中一个重大的挑战。
目前,不完整多视角数据的降维方法主要分为两大类。第一类不考虑缺失数据的重构,旨在利用已有样本直接学习投影矩阵及样本的低维表示。2010 年,KIMURA 等人[24]将典型相关分析(CCA)[25]与主成分分析(PCA)[13]的广义特征值问题结合,提出一种不完整两视角数据降维方法Semi-CCA,希望在最大化两视角间成对样本低维表示相关性的同时,保持每个视角数据的全局结构,最终利用已有数据分别求出两个视角的投影矩阵,但仅限于两视角的问题,并且只适用于线性数据。对于非线性数据,TRIVEDI 等人在KCCA(Kernel CCA)[26]的基础上提出了MCIV[27],基于不同视角间的核矩阵一致性的思想重构核矩阵,然后再应用KCCA 对重构后的多视角数据降维。但是,这种方法要求至少有一个完整视角,这在实际应用中是难以实现的。
第二类降维方法通常基于某些前提假设补全缺失数据,希望能够减轻不完整数据对后续学习任务的影 响。2015 年,XU 等人 提出了MVL-IV[28],基于低秩假设进行矩阵补全。同时,考虑到多视角数据的一致性[29-30],希望利用矩阵分解得到所有视角共同的低维表示,但是这种方法只是单纯地将多视角投影到一个公共子空间,没有考虑到数据的结构信息。TAO 等人[31]提出用低秩矩阵近似不完整视角,并通过线性变换学习完整的公共嵌入。此外,为学习到更加合理的低维嵌入,引入了块对角结构先验正则项。2018 年,YANG 等人[32]基于同一视角下样本的线性相关性与不同视角间同一样本对应的低维表示应该相似[33-35]地假设线性重构缺失样本,同时引入图嵌入项来保持原始空间的局部结构,但是该方法只考虑了完整样本,忽略了重构样本的作用,造成了一定程度的信息损失。ZHANG 等人[36]通过引入不同视角间的一致分布约束进行特征级的缺失数据补全,同时通过构建特征同构子空间来捕捉不同视角间的互补性。
本文提出一种基于双重局部保持的不完整多视角降维方法(DLPEL)。利用不同视角间的局部结构一致性以及同一视角下样本的线性相关性来线性重构缺失样本,并构造所有样本点上的图来学习所有视角的公共低维嵌入。在此基础上,为权衡缺失样本对学习结果的影响,设计一个权重来度量样本的可靠性。
1 相关工作
1.1 局部线性嵌入
局部线性嵌入(Locality Linear Embedding,LLE)[37]认为数据在局部是线性的,即某个样本可以被它邻域内的样本线性表示,希望降维后能保持高维空间的局部线性结构,是一种无监督非线性降维方法。已知数据集X=(x1,x2,…,xm)∊Rd×m,其中,m为样本个数,d为维度,LLE 希望学习m个样本的低维表示y1,y2,…,ym。
用样本xi的近邻点对xi进行线性重构,计算线性相关系数向量wi=(wi1,wi2,…,wim)∊R1×m。优化问题如下:
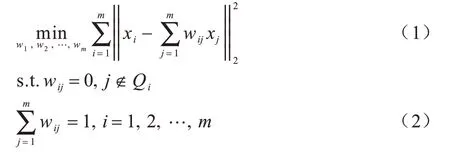
其中,Qi为样本xi的近邻点下标集合。LLE 希望低维样本间的局部线性相关性与原始数据一致,即线性相关系数wij保持不变。优化问题如下:

由式(3)即可求出原始样本的低维表示y1,y2,…,ym。
1.2 局部保持投影
局部保持投影(Locality Preserving Projection,LPP)[38]是一种经典的线性降维方法,其目标是学习一个投影矩阵P,将原始数据投影到低维子空间中。LPP 希望找到的投影矩阵P能够保持原始数据的局部近邻结构,优化问题如下:

其中,Wij表示样本xi和xj的相似度,可以根据不同的要求定义Wij,如下:
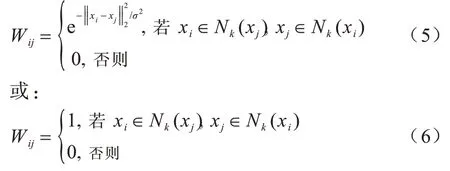
其中,σ为热核参数,Nk(xi)表示xi的k个近邻点的集合,但是LPP 只能处理单视角数据,如何将LPP 应用于多视角场景仍是一个值得思考的问题。
2 本文模型
对于不完整多视角数据,本文考虑部分样本在所有视角下完整,而其余样本只有部分视角,即缺失样本的整个特征向量在某些视角下缺失的情况。本文模型希望学习所有视角的公共低维嵌入。
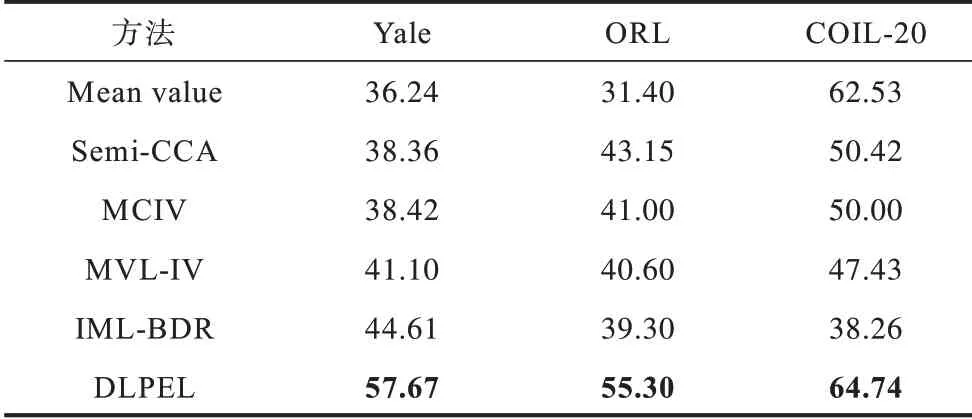
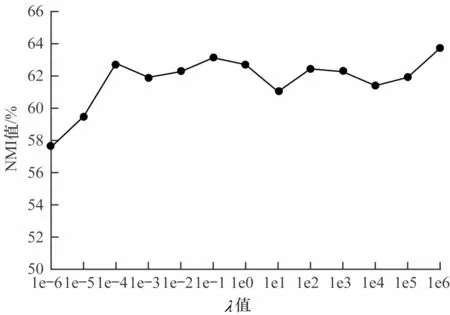
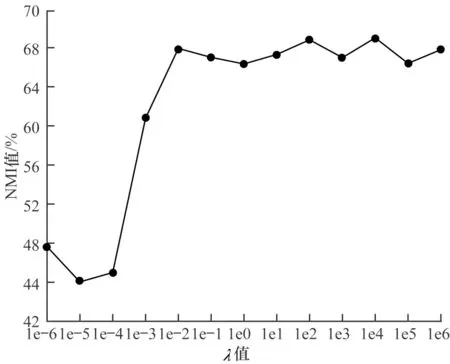
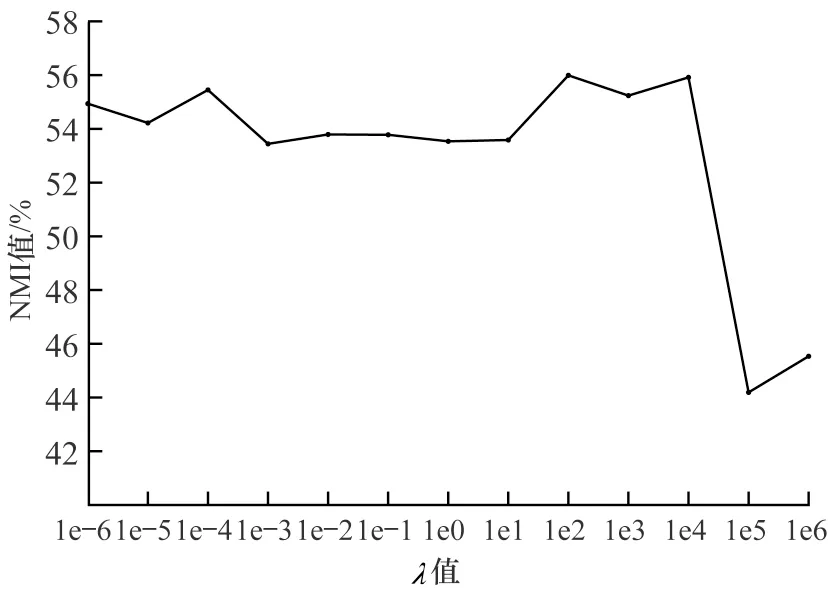
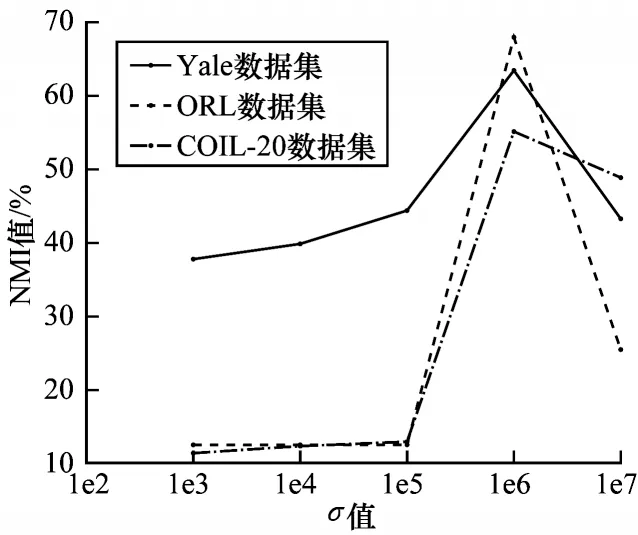
已知N个样本,共有s个视角,第v个视角的数据矩阵为,v=1,2,…,s,共有nv个缺失样本,Iv表示第v个视角的缺失样本下标集合,Vi(i=1,2,…,N)表示第i个样本的完整视角标号集合,即若v∊Vi,则第i个样本在第v个视角下是完整的。本文称在所有视角下完整的样本为成对样本。为便于解释,将前p(p 图1 不完整多视角数据的场景Fig.1 Scenario of incomplete multi-view data 本文方法是一种两阶段方法。第一阶段线性重构缺失样本,第二阶段求所有视角在d维公共子空间中的低维嵌入Y=[y1,y2,…,yN]∊Rd×N。 本文认为同一视角下的不同样本不是独立无关的,它们之间具有一定的线性相关性[31],某个样本可以被其余样本线性表示。基于这一假设,对于缺失样本(i∊Iv,v=1,2,…,s),希望利用第v个视角下的所有成对样本对进行线性重构。但由于样本的缺失,不能像LEE 一样直接求出对应的线性相关系数向量。考虑到多视角数据的一致性,认为不同视角下的样本应该具有相同的局部线性关系。因此,首先计算其他完整视角中第i个样本(u∊Vi)关于成对样本矩阵的重构系数向量∊Rp×1。对于任一i∊Iv(v=1,2,…,s),u∊Vi,优化问题如下: 通过求解上述优化问题,获得了第i个样本在所有完整视角下关于成对样本的重构系数向量。考虑到视角间的相似程度不同,引入一个新的权重αu(u∊Vi),可以度量第u个视角与第v个视角的相似度。结合式(7),对任一i∊Iv(v=1,2,…,s),有以下最小化问题: 每个视角都对应一个非负权重αu,αu越大,表明第u个视角与第v个视角的相似度越高。计算出所有完整视角的权重αu及重构系数向量,就可以用第v个视角下的所有成对样本线性重构缺失样本: 在第2 阶段,基于重构后的完整多视角数据,希望学习所有视角公共的低维Y=[y1,y2,…,yN]∊Rd×N。与LPP 相似,希望Y能够保持原始空间的局部结构。但LPP 不能直接应用于多视角数据,一种自然的方式是对所有s个视角求和,优化问题如下: 其 中,Sv∊RN×N是所有样本的邻接矩阵,定 义如下: 传统的基于图的降维方法如LPP 等都是先学习原始空间的局部结构。显然,如果原始数据有误差或噪声,那么这种误差也会传递到所学的数据结构中。考虑到重构后的数据可能是不精确的,会给最终的学习结果带来一定的误差。因此,本文设计了一种权重来减轻重构样本对模型的影响,如(14)所示: 其中,惩罚参数zij定义如下: 其中,‖˙‖1是l1-范数,M(:,i)表示矩阵M的第i列,称M∊Rs×N为缺失样本指示矩阵: 其中,惩罚参数zij可以度量样本对和的可靠度,样本对的可靠度越低,权重越小,进而缺失样本对目标函数式(11)的影响越小。 此外,考虑到多视角数据的互补性,认为每个视角对学习公共嵌入Y的贡献都不同。因此,引入一个权重向量β=(β1,β2,…,βs)∊R1×s,权重βv越大,表明第v个视角的贡献越大。最重要的是,当样本对中包含缺失样本时,对应的权重就更小,这样可以减轻缺失样本对目标函数的影响。同时,保证了公共子空间能够保持原始空间的局部几何结构,最终的优化问题如下: 对i∊Iv,v=1,2,…,s,由于优化式(8)、式(9)是有非线性约束的非凸问题,不能直接计算出全局最优解,本文设计了一种交替迭代优化算法来获得问题的局部最优解。 其中,ei∊RN×1为第i个元素为1,其余均为0 的列向量,Ip×p是一个单位矩阵,O(n-p)×p为全0 矩阵。因此,关于αu的子问题形式如下: 重构阶段的迭代过程如算法1 所示。 算法1重构阶段 与重构阶段类似,优化问题式(19)、式(20)是有非线性约束的非凸问题,无法找到其全局最优解。因此,本文设计了一种交替迭代优化算法来求问题的局部最优解。 1)固定β,更新Y。 给定权重向量β=(β1,β2,…,βs),关于Y的子优化问题如下: 其中,L=,故全局最优解Y是由L的前d个最小特征值对应的特征向量组成的矩阵。 2)固定Y,更新β。 已知低维嵌入Y,关于β的子问题形式如下: 求解权重向量β的方法此处不再赘述,详情可见3.1 节。下面给出βv的形式: 降维阶段的迭代过程如算法2 所示。 算法2降维阶段 本节将在3 个经典的图像数据集上,通过数值实验与一些相关的不完整多视角降维方法进行比较,并根据K-means 聚类结果验证本文模型的有效性。 实验中用到的3 个图像数据集如下: 1)Yale 人脸数据集由耶鲁大学计算机视觉与控制中心创建,包含15 个人的165 张人脸图像。每个人有11 张图像,分别对应快乐、正常、悲伤、困倦、惊喜、眨眼、左侧光、右侧光、戴眼镜和不戴眼镜等不同的面部表情、光照条件或姿态,图2 为其中一人的11 张图像。 图2 Yale 人脸数据集中某人的11 张图像Fig.2 11 images of one person in the Yale face dataset 2)ORL 人脸数据集由剑桥大学AT&T 实验室采集,包含40 个人的400 张人脸图像。实验室在不同的时间以光照条件、面部表情和面部饰物为变量给每个人拍摄了10 张照片。 3)COIL-20数据集来自哥伦比亚大学图像数据库,包含20 个物体,如图3 所示。每个物体旋转360°,每隔5°拍摄一张照片,因此数据集共有1 440 张照片。 图3 COIL-20 数据集中的20 个物体Fig.3 20 objects in the COIL-20 dataset 本文运用3 种广泛应用的指标度量聚类结果的好坏,分别是准确率(ACC)、标准化互信息(NMI)和纯度(Purity)。 其中,n为样本个数,yi和ci分别代表第i个样本的真实标签和聚类标签,map(˙)是一个排列函数,可以利用匈牙利算法对齐真实标签和聚类标签[39],δ是一个指示函数,若yi=map(ci),则为1,否则为0。 其中,TTL和CCL分别表示真实标签和聚类标签,I(TTL;CCL)表示TTL和CCL间的互信息,度量聚类结果与真实标签间的相似程度,E(˙)表示变量的熵,引入分母是为了将互信息的值标准化到[0,1]之内。 其中,k为簇的个数,ni为第i簇的样本数,pij=为第i簇中的样本属于第j类的概率,nij为第i簇中的样本属于第j类的个数。 本文选择了近几年具有代表性的5 种不完整多视角降维方法,包括Mean value、Semi-CCA[24]、MCIV[27]、MVL-IV[28]、IML-BDR[31]。其 中Mean value 利用同一视角下的完整样本平均值补全缺失样本,使用本文的多视角降维方法对学习到的嵌入进行K-means 聚类,其他几种对比方法的更多细节见概述部分。 从数据集的图像中提取出灰度值强度(GSI)、方向梯度直方图(HOG)和局部二元模式(LBP)3 个视角的特征,得到3 个完整的多视角数据集。为去除原始特征的冗余信息,利用主成分分析(PCA)对数据预处理。通过构造不完整数据集,随机选取70%的样本作为成对样本,然后在每个视角剩余的样本中分别选取10%的样本用1 填充。由于MCIV 要求至少有一个完整视角,因此在第2 个、第3 个视角中选取15%的样本作为缺失样本,并用1 填充。 在Yale、ORL 和COIL-20 数据集上的实验结果如表1~表3 所示,分别对应ACC、NMI 和Purity 值,值越高,证明模型的性能越好,其中黑色粗体表示最优结果。 表1 Yale、ORL 和COIL-20 数据集上的ACC 结果Table 1 ACC results on Yale,ORL and COIL-20 datasets % 表2 Yale、ORL 和COIL-20 数据集上的NMI 结果Table 2 NMI results on Yale,ORL and COIL-20 datasets % 表3 Yale、ORL 和COIL-20 数据集上的Purity 结果Table 3 Purity results on Yale,ORL and COIL-20 datasets % 从表1~表3 可以看出: 1)与DLPEL 方法相比,Mean value 方法的聚类结果更差。这表明直接用均值向量填充缺失样本是不合理的,并且这种补全方式影响了后续的聚类。本文模型利用了多视角数据的一致性,更好地实现了缺失样本重构。 2)MCIV 方法要求至少有一个完整视角,该方法可以更好地利用多视角数据的互补性,但仍没有DLPEL 方法效果好,表明了本文方法处理一般不完整多视角数据的有效性,可以更广泛地应用到实际问题中。 从以上结果可以看出,本文方法DLPEL 在3 个数据集上相比其他方法都具有更好的性能。 参数λ负责调节重构误差项与正则项之间的平衡,本文应用本文模型DLPEL 将样本降到40 维后进行K-means 聚类,通过在Yale、ORL 和COIL-20 数据集上的实验结果分析了模型关于参数λ的敏感度。 由图4~图6 可知,DLPEL 关于参数λ较为敏感,当λ锁定在[1,104]的范围内时,可以达到较为理想的聚类效果。在实验过程中发现,高斯核参数σ的变化对模型的影响很大,当先固定λ=103,d=40,然后在Yale、ORL、COIL-20 数据集上进行实验,寻找最优的参数σ。从图7 可以直观地看出,随着σ的变化,NMI 的值波动很大。当σ=106时,本文模型在3 个数据集上都展现了最优越的性能。因此,将所有实验中的参数σ均设为106。 图4 Yale 数据集上NMI 随λ 变化的折线Fig.4 Line chart of NMI changes with λ on Yale dataset 图5 ORL 数据集上NMI 随λ 变化的折线Fig.5 Line chart of NMI changes with λ on ORL dataset 图6 COIL-20 数据集上NMI 随λ 变化的折线图Fig.6 Line chart of NMI changes with λ on COIL-20 dataset 图7 Yale、ORL 和COIL-20 数据集上NMI 随σ 变化的折线Fig.7 Line chart of NMI changes with σ on Yale,ORL and COIL-20 datasets 本文结合多视角数据局部结构的一致性与特征空间的线性结构,提出一种基于双重局部保持的不完整多视角降维方法。通过引入一个惩罚参数,减轻了缺失样本对学习结果的影响,得到了保持原始数据局部结构的公共低维嵌入。实验结果表明,与MVL-IV 算法相比,该方法可以获得较好的聚类结果,验证了本文模型处理不完整多视角数据时的有效性。本文模型分两阶段考虑了缺失数据的补全和降维,但有可能导致算法的性能退化,下一步将提出一个统一的目标函数,在补全数据的同时获取样本的低维表示,通过两者的相互促进提高算法的性能。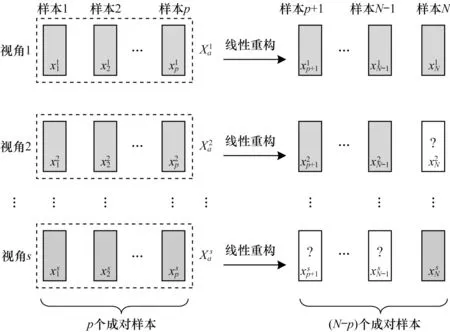
2.1 基于局部线性保持的缺失样本重构


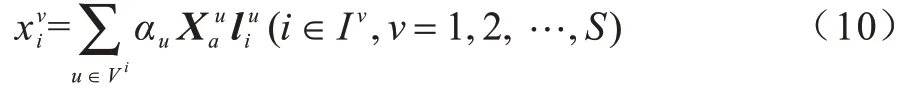
2.2 基于局部结构保持的嵌入学习
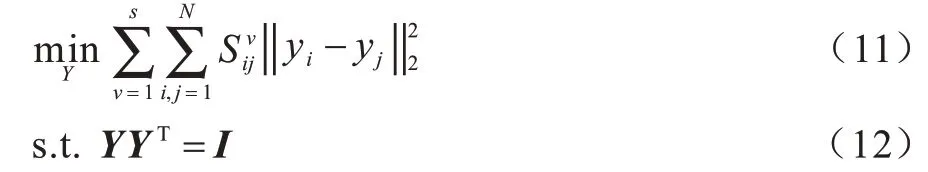





3 优化方法
3.1 重构阶段



3.2 降维阶段




4 实验
4.1 数据集


4.2 评价标准
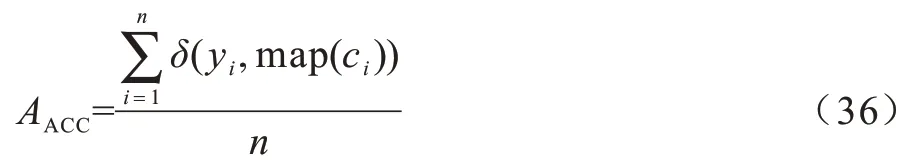
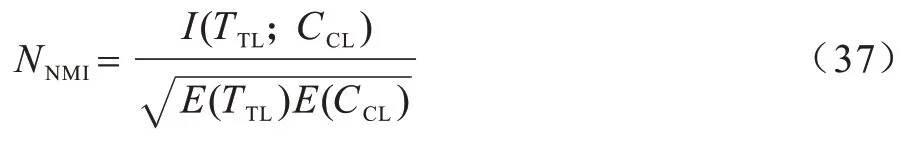

4.3 对比方法与实验设置
4.4 实验结果


4.5 参数分析
5 结束语

