基于Lundberg-Palmgren理论的行星轮系齿轮点蚀疲劳寿命计算
胡耿, 陈志刚
(1.中国航发湖南动力机械研究所,湖南 株洲412002;2.直升机传动技术国防科技重点实验室,湖南 株洲412002)
0 引言
齿面点蚀是齿轮材料在循环接触应力作用下,由于疲劳而产生的麻点状损伤现象,多发生于润滑良好的闭式齿轮传动中。对于点蚀疲劳,标准AGMA 2101-D04给出了内外啮合直齿和斜齿齿轮抗点蚀能力的计算方法,该方法假设当齿面抗点蚀能力满足设计要求时即具有无限寿命。然而轴承点蚀疲劳试验和应用经验表明,其滚子和滚道的接触疲劳寿命是有限的,因此部分学者[1-2]认为:齿面接触疲劳寿命应是有限的,而不是无限的;Rumbargur[3]基于Lundberg-Palmgren理论提出了圆柱直齿轮的寿命和失效概率关系模型;Zaresky等[4]给出了9310钢齿轮的疲劳试验数据,并证明了理论计算与试验结果具有较好的符合性。
目前国内对该计算方法的公开报告和研究较为少见。本文在综合分析外啮合计算模型的基础上,提出了内啮合齿轮点蚀寿命计算方法,并运用该方法对某行星轮系减速器的齿轮点蚀寿命进行了计算分析。
1 Lundberg-Palmgren理论
Lundberg-Palmgren理论(LP理论)由Lundberg于1947年提出,已经在轴承行业得到了广泛应用,并成为了滚动轴承寿命计算分析的基本方法,其方程为
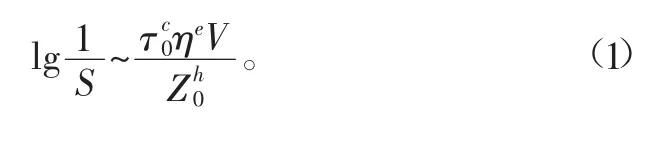
式中:S为零件存活率;V为应力影响区体积;η为应力循环数,106次;e为威布尔系数;h、c为材料常数;z0为最大剪切应力深度,mm;τ0为最大剪切应力。
2 外啮合圆柱齿轮点蚀寿命计算方法
2.1 单个轮齿点蚀寿命计算
Zaretsky在LP理论的基础上开展了齿轮疲劳试验,并提出了外啮合圆柱齿轮点蚀寿命计算方法[5]。类似轴承,轮齿的基本额定寿命定义为一组齿轮中90%轮齿不发生点蚀破坏前的转数;轮齿的基本额定动载荷为当轮齿的基本额定寿命为106次时所能承受的最大载荷。根据文献[6],轮齿基本额定动载荷公式为
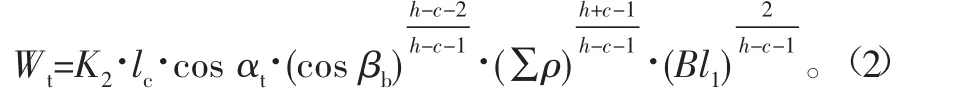
式中:K2为比例系数,由点蚀疲劳试验确定,取5.28×108;αt为端面压力角,(°);βb为基圆螺旋角;B为轮齿宽度,mm;lc为齿面接触线长度,lc=B/cos βb,mm;l1为轮齿上啮合接触区域沿齿高方向的长度,mm;Σρ为一对啮合轮齿的综合曲率半径;h和c均为材料常数,根据试验统计结果,h=2.7525,c=23.2525。
对于外啮合齿轮,根据赫兹定理,综合曲率半径Σρ的计算公式为

啮合线l1计算式为

式中:rb1为齿轮基圆半径;θ U1为轮齿脱离接触的滚动角;θL1为轮齿开始接触的滚动角;θU1= θL1+ βH1,β H1为单齿啮合区对应的滚动角,r a d ;θL1= δ1+ βL1,δ 1为啮合前轮齿滚动角(如图1),r a d ;β L1为双齿啮合区对应的滚动角,r a d 。
外啮合齿轮,其啮合前转动角为
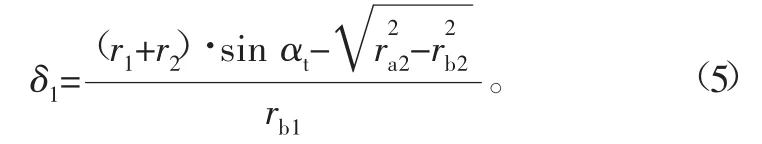
βL1和β H1计算式分别为:

式中:P b为基圆齿距;ξ 为实际啮合线长度。
对于外啮合齿轮,其实际啮合线长度ξ 的表达式为
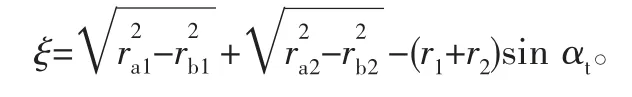
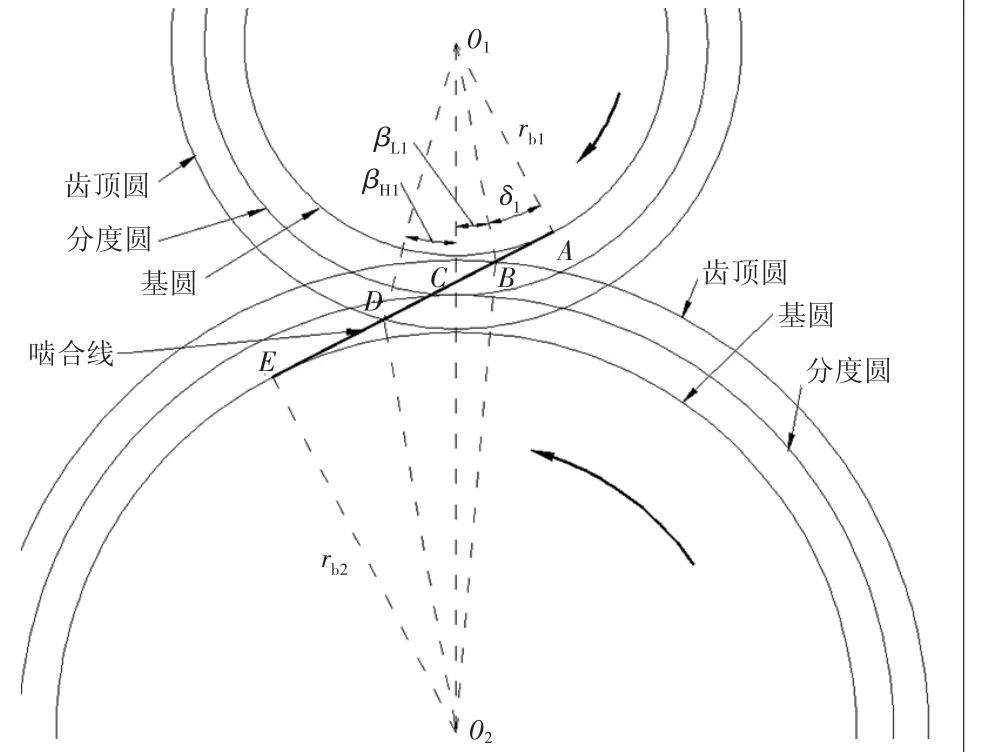
图1 外啮合齿轮滚动角示意图
在齿面接触载荷F t作用下,单个轮齿的点蚀寿命为
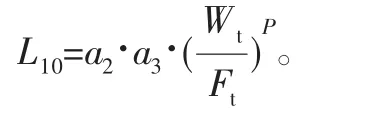
式中:p 为载荷寿命因子,通常p = 4 .3 ;a 2为材料修正系数,由齿轮材料和性能决定;a 3为润滑修正系数,由润滑条件和轮面质量决定,其取值详见文献[6 ]。
2 .2 齿轮副的寿命计算
如果单个轮齿的存活率为S 1,根据概率论,则齿轮(N 1个轮齿)存活率S P为

一对齿轮啮合副的存活率S M 取决于相互啮合的大、小齿轮的存活率S P和S G,则齿轮啮合副的存活率为

式中,N 1和N 2分别为主、从动齿轮的齿数。
3 行星轮系点蚀寿命计算方法
在常用的N G W 行星轮系中,太阳轮与行星轮的点蚀寿命可以直接用式(2)来计算,但式(2)的推导是建立在外啮合齿轮的基础上,因此不能直接用于内齿圈和行星轮的点蚀寿命计算,需要进行相应调整。
3 .1 综合曲率半径
外啮合齿轮齿面接触属于外接触,而内啮合齿轮属于内接触。根据赫兹理论,内啮合齿轮的综合曲率半径Σ ρ 为
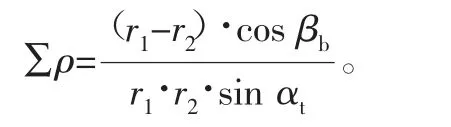
3 .2 实际啮合线长度
对于内啮合齿轮,其实际啮合线长度为
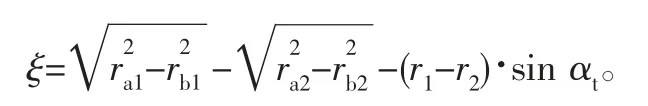

图2 内啮合齿轮啮合线示意图
3 .3 啮合前转动角δ 1
啮合前转动角是指小齿轮沿啮合线从基圆开始转动到与大齿轮接触之前转动的角度。对于对内啮合齿轮, 啮合前转动角为
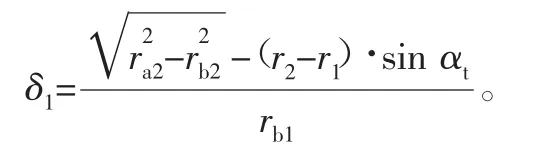
3 .4 行星轮点蚀寿命计算方法
在行星轮系中,行星轮的两侧齿面均存在啮合接触,其中一侧齿面与太阳轮接触,另一侧齿面则与内齿圈接触。因此,行星轮齿轮的点蚀失效概率会更高。根据概率准则,行星轮单个轮齿的点蚀寿命计算公式为
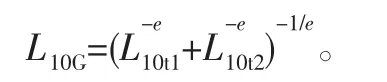
式中,L t1和L t2分别为行星轮与太阳轮、内齿圈啮合的齿面的点蚀疲劳寿命。
4 计算算例
某大功率发动机减速器采用行星轮系构型:输入齿轮轴与发动机动力涡轮轴相连,2 个输出轴分别驱动两排桨扇。该差动轮系各轮齿参数如表1 所示,工况参数如表2所示。

表1 减速器轮齿参数

表2减速器工况参数
表3为行星轮系各齿轮计算结果,结果表明:太阳轮的点蚀寿命最短,内齿圈的寿命远大于太阳轮和行星轮,轮系齿轮总点蚀疲劳寿命为6.08×106h。

表3齿轮计算寿命
5结语
本文在总结国外齿轮点蚀寿命计算的基础上,提出内啮合齿轮点蚀寿命计算与外啮合齿轮存在一定的区别,应对综合曲率半径、啮合线长等计算进行调整,并在此基础上对某行星轮系的齿轮点蚀寿命进行了计算。计算结果表明:所有齿轮中,太阳轮的点蚀寿命最低,内齿圈的寿命显著高于太阳轮和行星轮。

