基于神经网络的航空发动机故障诊断

丁一然

（北京交通大学附属中学，北京，100081）

0 前言

航空发动机是一个高转速机械系统[1]，其工作环境较为苛刻，长时间在高温、高压、高应力和强腐蚀的环境下运行，因此极易发生故障，如腐蚀与打击，从而为航空发动机带来一定停车故障甚至毁灭性的破坏[2]。所以，航空发动机的故障诊断可以有效提高航空发动机的续航和工作效率，并减少发生事故的可能性。但由于航空发动机结构复杂和部件数量多，导致其故障类型繁杂，会存在包括有关气路、油路和振动等一系列的故障问题，而在气路故障中又会包含如积垢、热变形、密封件疲劳、腐蚀等具体的故障[3]，振动故障也会包括如风扇失速振颤、叶片裂痕等具体故障[4]。其中对于不同类别的故障类型其导致产生的关键因素也会有所不同，如叶片转速、叶片的实际压力值等可作为导致振动故障的因素，发动机进气口温度、压气口的压力[2]等可作为导致气路故障的因素。因此由于故障类型的繁杂使得以往基于纯模型或基于知识[3]对于故障进行分析的方法不易实现。

神经网络作为20世纪兴起的基于生物神经网络而构建的人工数学模型，有着自主分类和自我学习的功能，且随着Geoffery Hinton等人在21世纪初建立的多层神经网络（深度学习）的兴起，可用于解决的问题范围又得到了进一步的扩展。基于神经网络对航空发动机进行故障的分析可借助神经网络突出的自我分析和学习能力，快速并基本准确的得到问题的最优解，判断故障的发生和类型，进而预测并避免发动机故障的发生。

梅家崎[5]利用主成分分析的方法提取故障数据的主要参数，利用神经网络构识别模型，并且对比多层感知机神经网络和自组织网络的结果差异。李洪伟[6]将振动信息和油液信息融合，采用模糊综合决策方法对各个子网络信息的诊断结果进行综合决策。基于集成神经网络故障诊断法，并与光谱诊断和振动诊断作对比，结果显示这种这种方法的效果更好。于宗艳[7]采用带惯性项的批处理算法，对航空发动机故障数据进行神经网络训练，结果显示该神经网络算法可以有效提高识别正确率。郭风[8]利用RBF网络构建航空发动机的故障模型，对多参数故障信息进行分析，结果表明RBF对11个故障具有准确分析能力。王亚凡[9]采用自适应加权D-S证据理论对发动机气路部件进行故障诊断，通过分析多证据融合过程中的证据严重冲突，赋予不同的概率函数的权值，从而降低证据冲突。

本文主要是通过构建基于附加动量权值方法和变学习速率方法的BP神经网络，对航空发动机故障进行诊断。对于包括气路、油路、振动等复杂故障类型的航空发动机故障分析，本文对提取监测参数变化和发生故障的数量特点，构建本文神经网络训练学习的样本数据，从而检测本文构建的神经网络预测能力，可以达到预测航空发动机的故障发生、发生的故障类型的目的。

1 模型建立

■1.1 神经网络原理

神经网络是由多个“神经元”(又称节点)，按照不同层次排列所构成的网络，网络拓扑结构由输入层、隐含层和输出层组成。神经元是神经网络的基本单位，经典的神经元模型包含输入值和权值以及输出值。神经元数学表达式为：

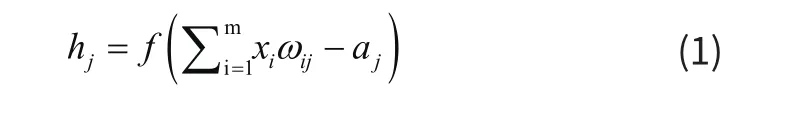
其中，xi为输入值，wi,j为权值，aj为隐含层阈值，hj为隐含层输出值， f ( x)为激励函数。

本文主要采用的神经网络模型是BP神经网络。BP神经网络最主要的特点是数据向前传递，即从输入层到输出层，而网络预测误差则是反向传递得到更新后的权值[10]。BP神经网络中隐含层数量可以分为单层和多层，隐含层数量越多，网络预测结果精度越高，同时也会大大增加网络训练时间。在神经网络预测中用来评价预测结果的准确性的是损失函数，也称为误差函数，其可以简单表示为：

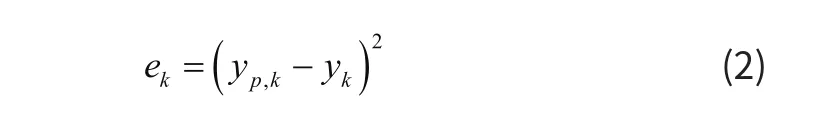
其中，yp,k为网络预测目标，yk为训练样本真实值。通过误差结果可以得到新的各层之间的权值。以单隐含层BP神经网络为例，更新公式如下：

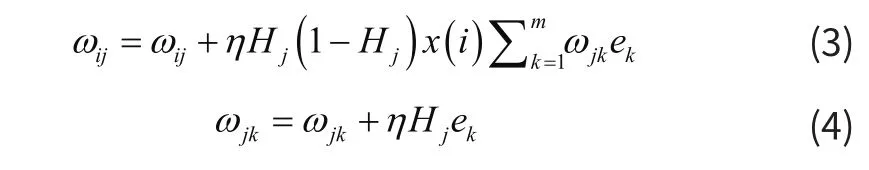
其中，η为学习速率。

为提高神经网络学习过程中收敛速度，本文采用附加动量方法和变学习速率方法分别对权值和学习速率进行修正[10-12]。附加动量方法的权值学习公式在原BP权值公式的基础上考虑以前权值对当前时刻权值的影响，修正后的权值学习公式为：

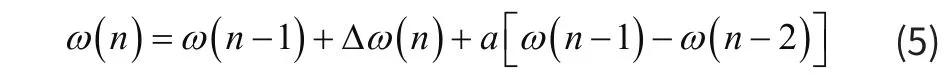
其中，ω (n −2)，ω(n −1)，ω( n )分别为n−2，n−1，n迭代次数的权值，a为动量学习率。变学习率方法则是指初期的学习率较大，加速网络收敛，而在学习的过程中，学习速率逐渐降低，使得收敛稳定，变学习率公式为：

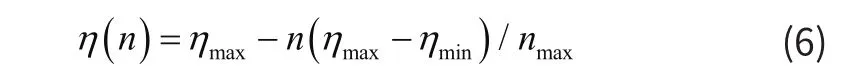
其中，ηmax和ηmin分别为最大和最小学习率，nmax为最大迭代次数。

■1.2 航空发动机故障数据及样本初始化

航空发动机的故障会由各种不同的原因引起， 而航空发动机发生故障会在航空发动机的某部分性能参数发生改变。同样的，这些性能参数可以在航空发动机的监测数据上得到反馈，如温度、效率、压力等物理参数[9]。本文对航空发动机的故障分析便是通过对航空发动机的监测数据进行分析，无需直接观察或测量性能改变，而得到发动机的故障类型和故障数量。本文的分析依据在于航空发动机的可测量参数的改变与航空发动机的结构和工作原理相关，往往某部件的故障会产生固定的几类参数的改变，从而提供逆推故障原理的可能性[9]。但是，由于航空发动机的结构复杂和部件数量多，并且可能多故障类型同时发生，给逆推分析故障原理带来难度，从而需要新的故障诊断手段。本文根据如气路、油路、振动等故障的大类型中选择若干作为研究对象，并考虑大故障类型中的小故障同时发生的情况，对故障类别按照规定标准进行划分。

鉴于航空发动机的监测参数众多，往往对监测参数进行归一化、主成分分析[5]等方法，提取主要特征参数及变化。根据发动机故障特点，可以分为单故障和双故障[9]。假设4个部件的监测参数分别为并且划分的故障总计为10种，如表1所示。部件的监测参数可以由实际的数据简化为隶属度函数或归一化指标。监测参数的数值范围为[0,1]，监测参数采用不同的标准会产生不同的故障分类。例如以0.5为标准，超过0.5处于大恶化或蜕化，小于等于0.5处于小恶化或蜕化。因为本文中故障参数并未指定具体部件，不失一般性的假定，4种部件中的两种以标准0.3简化，其余( ∆ S E3, ∆ S E4)以0.5简化。更进一步为了表示故障之间的恶化并不是独立发生，假设∆SE1是与∆SE2有关联，如果∆SE1是大恶化的前提下， ∆ S E2是大恶化的概率为60%，而∆SE1是小恶化的前提下，∆SE2是大恶化的概率为30%。

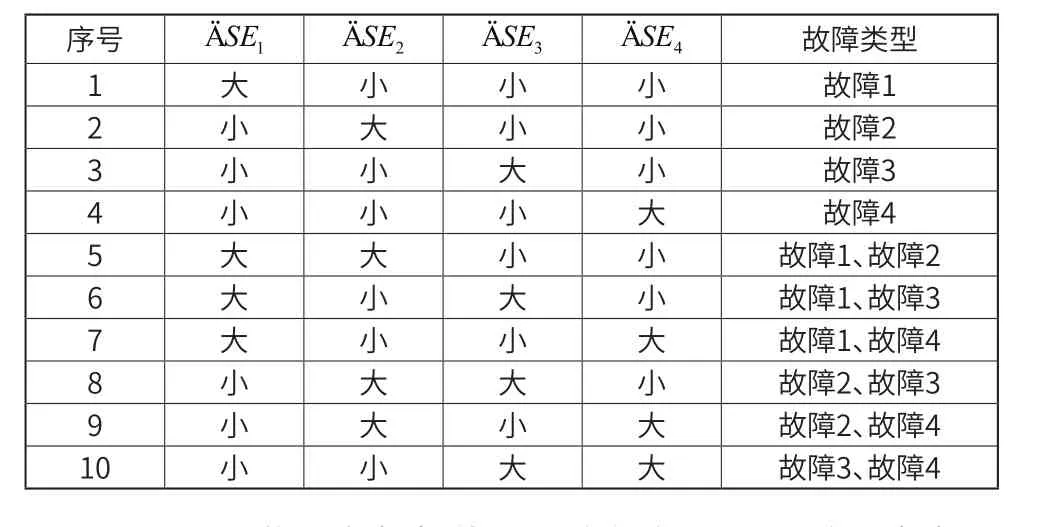
表1 故障分类

假设不同监测参数数值可以均匀在[0,1]分布，根据4种监测参数的不同恶化标准，可以判断出不同的故障类型。图1中的两幅图分别表示的了不同恶化标准下不同类型故障占总样本比例。不难看出无论在何种情况下样本获得的监测参数为正常情况（图中的故障类型11）的数量占比都是最大的，大约在45%左右。同时由于 ∆ S E1, ∆ S E2之间存在着相互影响的关系，监测参数 Ä SE1发生大恶化的情况下SE2会更容易发生恶化，而相反情况下ÄSE2也更不容易发生恶化，因此从图中也不难发现，故障2的数量相比较于故障1总是要少一些，而另一方面故障5（ ∆ S E1, ∆ S E2均为大故障）的数量则要比故障1、2的数量更多。图1(a)中可以发现，故障2、故障8和故障9的数量较少，反观图1(b)中则是故障1、故障2和故障5的变得相对较少，而原本数量中等的故障3、故障4和故障10却变多了，这说明不同的恶化标准会对数据的判断产生不同的结果，因此在样本数据初始化的过程中，应当选择一个合适的恶化标准，以便后续故障分析的统一与结果的有效。本文采取∆SE1和 ∆ S E2标准为0.3，∆SE3和 ∆ S E4标准为0.5的数据作为研究对象。

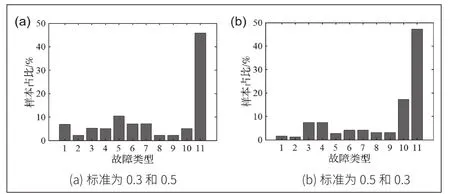
图1 不同故障类型占总样本比例

2 论文结果分析

■2.1 故障与正常样本分类

本文在对样本数据进行预处理后，开始对样本数据进行训练。训练结果表明，神经网络对故障的判断存在一定误差，正确率约为87%。同时，由于仅仅是判断正常和故障两种类型(记误差为1，正常为0)，因此存在分类误差达到1或-1的情况。

利用神经网络对故障类型进行诊断一般都会存在误差，而其判断的正确率又受到多种因素的影响，本文主要研究了中间层（即隐藏层）的数量、学习速率、训练次数和训练样本比例对于正确率的影响。中间层的数量对于分类的正确率影响不大，相比于中间层数低于10层，中间层数的提高，正确率会有微小的提升，中间层大于10层后便无明显的影响，后期甚至会有小幅下降。与其趋势相近的是训练次数对于正确率的影响，但其变化幅度明显比中间层的数量的要大，说明其对于诊断正确率的影响要大与中间层，不过两者相似的地方在于两者对于正确率的影响都会在达到某一数值后趋于平稳，如训练次数达到50次。而学习速率对于正确率的影响则没有太大的规律，在学习速率在0.2以内时，且对正确率的影响不太明显，但超过0.2后无论是对正确类别正确率、故障类别正确率还是总体正确率都有明显的影响。综上所述，神经网络设置为中间层10、循环次数50、学习速率0.2、训练样本比例0.7，训练结果较好。

■2.2 10种故障类型

本文在对正常与故障进行分类后又按照前文所述模拟分类方式，将故障分为十种类型，并设计第二个神经网络对其进行分类。从图2(a)中我们可以看出，与故障和正常类别的判断结果类似，对10种故障类型的分类(故障1记为1，故障2记为2，依次类推)也存在着一定的误差，且由于存在十种不同的类别，其误差的大小程度也不尽相同，但从图2(b)中可以发现，几乎不存在分类误差大于5的样本，说明本文采取采用的故障分析样本有一定的限制作用，将故障发生限制在一定范围内。

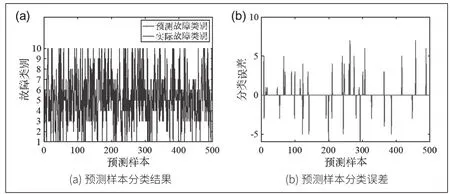
图2 神经网络预测结果

同样，为了更好完成神经网络对10种故障类型的诊断和分析，本文依旧从中间层数、训练次数、学习速率和训练样本比例四个要素，分析其对神经网络预测结果的影响。从图3中可以发现，除训练次数以外，其余的三种因素均对于该神经网络的正确率没有显著的影响，这表明了不同神经网络间确有差别，同时也提示了我们在该神经网络中，最主要的是要保证足够的训练次数，以得到较高的正确率。而其中训练次数对于正确率的影响体现为，当训练次数在50次以下时，随着训练次数的增加，正确率提高，但当训练次数超过50次之后，随着训练次数的增加，神经网络的正确率不会有明显的变化，这表明当前故障样本的最佳的训练次数在50次左右。虽然其他三个因素随对总体正确率没有显著的影响，但仍然存在对于单个类别正确率的影响，不过其对于单个类别正确率的影响没有较明显的规律性，可以归为随机事件不做特别考虑。因此，可以得到在故障诊断中要想得到较高的正确率，保证训练次数达到50次左右即可，但是随着故障类型的增加和数据样本的增加，需要将训练次数继续提高。

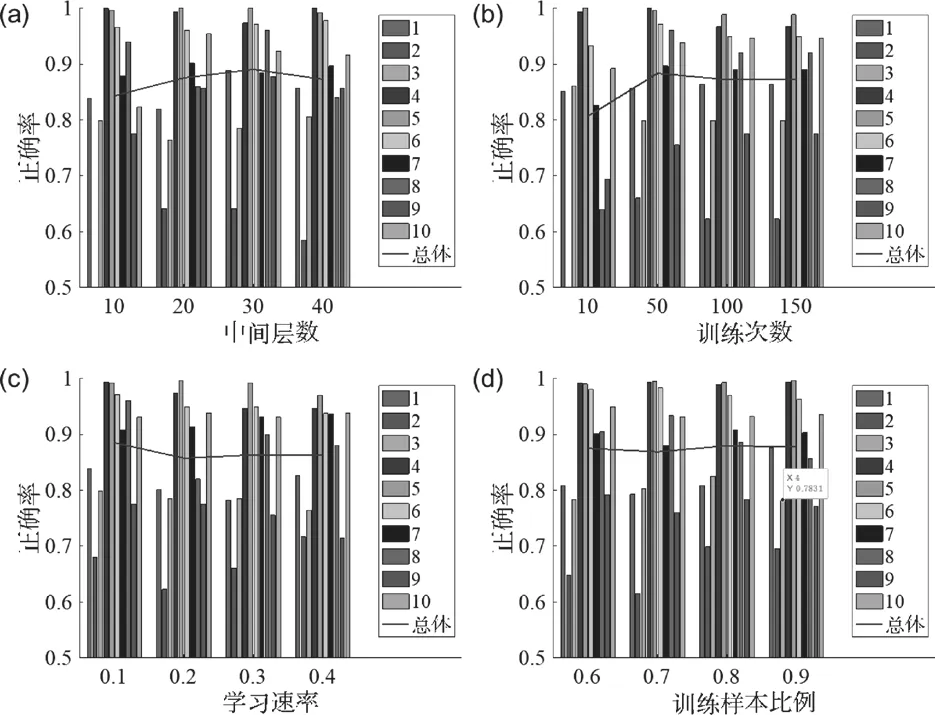
图3 不同神经网络设置参数对10种故障类型预测正确率影响.

3 结论

基于神经网络的航空发动机故障诊断，对于不同的故障判断分类方式构建预测数据和相应的神经网络，并针对神经网络的相关参数对故障诊断正确率的结果进行讨论与分析。神经网络的诊断结果对工程监测航空发动机的故障情况以及判断故障类型提供一定的依据。结果表明：

故障样本参数的判断标准会对不同故障类型的数量占比产生一定的影响，且在两种参数关联时，这种影响较为明显，但对正常状态下的监测参数，判断标准的影响较小。

神经网络的中间层数量、学习速率、训练次数、训练样本比例都对神经网络预测正确率有着一定的影响。其中，训练次数的影响最为显著，在本文故障数据的种类和数量规模下，训练次数为50次的效果最佳。