A Fully Distributed Approach to Optimal Energy Scheduling of Users and Generators Considering a Novel Combined Neurodynamic Algorithm in Smart Grid

Chentao Xu and Xing He

I. INTRODUCTION

IT is obvious that smart grid will occupy a very important position in the future distribution network system because it is more flexible, controllable, environmental than the conventional distribution network [1]. The users and generators can use the smart meters, advanced communication and control technologies to exchange information by the control center in the microgrid [2]. In general, at every time slot, the control center will announce the real-time price of energy according to the estimated demand, then the users will adjust their energy strategies for more benefits, which can decrease the demand at load peaks and increase demand at load valleys to make the distribution network system more stable and effective. At last the control center will buy the certain amount of energy from the generators according to their information [3]. Leeet al.[4] designed a smart lighting system for future smart grids. There are many types of loads in the user side and the models used to describe them are different. Haideret al.[5 ] analyzed the structure of the residential demand response systems and the load-scheduling techniques. Ihsanet al.[6] considered the generators with several types of renewable energy power. Xuet al.[7]structured the satisfaction function and designed the system model with three types of loads. Unlike gasoline car, there is huge market potential for electric vehicle (EV) because of its clean and environment-friendly advantages. It can be seen as energy storage devices at home with proper constraints.Karfopoulos and Hatziargyriou [8] gave two charging modes of centralized and distributed EV management control respectively. Luoet al.[9] combined two control strategies of series electric vehicles to get better fuel economy.

Neural network has developed quickly as a tool for solving optimization problems. Qinet al.[10] constructed a one-layer recurrent neural network to solve the constrained convex optimization problems with complex-variables. Xiaet al.[11]designed two projection neural networks with low dimension and complexity to solve the nonlinear programming problems.For general optimal problems with both equality and inequality constraints, Xia and Wang [12] gave some methods. Gao and Liao [13] presented a novel neural network to solve the generally constrained problems with fewer stability requirements. Hanet al.[14] used an artificial neural network to solve the quadratic zero-one programming problems. For many distributed systems, traditional centralized neural network algorithms are limited because they take a lot of computation with poor flexibility, the single point of failure will lead to global crash, etc. [15]. Therefore,distributed neural network algorithms have been used more and more widely in recent years. Yiet al.[16] proposed a distributed gradient algorithm for constrained optimal problems. Heet al.[17 ] put forward a second-order distributed continuous-time algorithm under a centralized framework. Jiaet al.[18] proposed a neural network to solve the distributed nonsmooth optimization problems with inequality constraints over a multi-agent network. Guoet al.[19] considered a new distributed gradient-based algorithm to accelerate the convergence speed.

Compared with the neural network algorithms, many other intelligent algorithms are also useful in solving optimization problems with different features. Particle swarm optimization(PSO) is well known for its excellent ability to find the global optimal solution [20]. It came from studying the predation behavior of birds and is an efficient parallel algorithm. There are many improved PSO algorithms in recent years for better performance. Jensi and Jiji [21] presented an enhanced particle swarm optimization with Levy flight to get better performance on benchmark functions. Nouiriet al.[22] used a distributed particle swarm optimization algorithm to solve the flexible job-shop scheduling problem. Differential evolution(DE) algorithm is popular as another parallel algorithm with evolutionary computing technologies since it was put forward.It is a random heuristic search algorithm with strong robustness and ability for global optimization [23]. Cuiet al.[24] designed an adaptive differential evolution algorithm with novel mutation strategies to enhance the optimization performance. Mohamed [25] introduced a novel differential evolution algorithm for solving constrained engineering optimization problems with better convergence rate. However,both of the two intelligent algorithms have two disadvantages.One is that they tend to fall into local optimal solutions and have difficulty to deal with complex constraints. The other is that they will take too much time when the optimization problem has enormous scale and variables. So, it is a good idea to combine the neural network algorithm with the intelligent algorithm so that it will take a short time to find the global optimal solution and the constraints can be dealt with effectively. Yanet al.[26 ] used a new neurodynamic algorithm which combined the neural network algorithm with PSO successfully. In this paper, we will try to combine the neural network algorithm with DE. This paper has four main contributions:

1) A fully distributed microgrid system which includes both the users and generators is constructed to protect privacy, get more benefits for users and make the distribution system more stable and efficient;

2) A zero-one variable is introduced to represent the two states of the electric vehicles;

3) A novel neurodynamic algorithm which combines the neural network algorithm with DE is designed to deal with the nonconvex optimization problem of the users;

4) A distributed algorithm with a new approach to deal with the inequality constraints is used to solve the convex optimization problem of the generators.

The remainder of this paper is organized as follows. The microgrid system model and the object problems are described in Section II and the algorithm description with convergence analysis can be seen in Section III. In Section IV, the simulation results of our algorithms and comparison algorithms are given. Finally, the conclusion is drawn in Section V.

II. SYSTEM MODEL AND PROBLEM FORMULATION

In this paper, we consider a microgrid structure with a control center,Nusers andMgenerators, which is shown in Fig. 1. A day is divided intoTtime slots with different real-

Fig. 1. The structure of the microgrid.

time prices for electricity generation and electricity purchase.At every time slot, the control center will exchange price and demand information by the smart meters with the users. The specific process is that the control center will announce the real-time electricity price of that time slot and the users will give their feedback of energy demand by weighing their interests against their satisfaction. Then, the control center will buy the needed amount of energy from the generators according to their price and capacity information. With the whole scheduling process, the users will get the most benefits and the microgrid system will reduce congestion and become more stable and reliable because demand will decrease during demand peak time slots and increase during valley time slots.

A. User

A user usually has three types of loads.

1) Type A:This type of load is fixed and must run at the certain time slot including lamps, refrigerators, etc.lAn(t)denotes the amount of energy of loadAconsumed by usernat time slott,n∈{1,2,...,N} andt∈{1,2,...,T}. Its constraint is as follows:

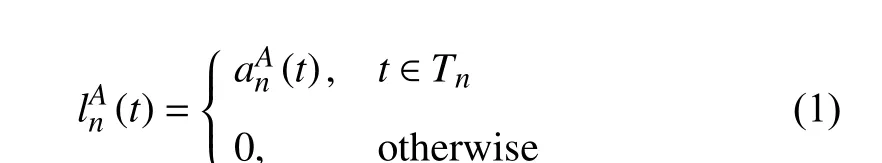
where α >0 is a weight factor to trade off the satisfaction and benefits.

The examples of the utility function are shown in Fig. 2.The satisfaction of user increases gradually when the actually consumed amount of power gets closer and closer to the target energy consumption. Once the target is reached, the satisfaction will not change even if the actually consumed amount of power continues to increase.

3) Type C:This type of load is the plug-in electric vehicle.It will be an important part of the households in the future because of its environmentally friendly feature. It can be seen as a rechargeable battery when at home. When the real-time electricity price is low, it can be charged and when the price is high, it can be discharged on the premise of satisfying its own charging demand, which can bring some benefits to the user.lCn(t) denotes the amount of energy of loadCconsumed by usernat time slott. In real life, the charging efficiency βcand discharging efficiency βdare nonnegligible. So, the actually amount of stored energy after charging and the actually amount of energy that needs to release during discharging are denoted as follows respectively:

It is obvious that loadCcannot charge and discharge simultaneously at a time slot, thus we use a zero-one variablexn(t)∈{0,1} to distinguish between these two states. Then, the actually value of stored or released energy is denoted as follows:

Whenxn(t)=1, the plug-in vehicle is in charged and the value ofen(t) is positive that represents the actually amount of stored energy after charging, whenxn(t)=0, the plug-in vehicle is in discharged and the value ofen(t) is negative that represents the actually amount of energy that needs to release during discharging.

We denote that the time slots for the plug-in vehicle to arrive and leave of usernaretn,aandtn,l, respectively, wheretn,a,tn,l∈{1,2,...,T}, then it schedules only between these two time slots so it has the following constraint:

Also, it has the following upper and lower bound constraint at every time slot:

We define that the amount of energy left over when the plug-in vehicle arrives isEn,aand the amount of energy required for travel when the plug-in vehicle leaves isEn,lof usern, then at every scheduled time slot, it should satisfy the following constraint:

At the last scheduled time slot, the plug-in vehicle should have enough energy for the next travel, which is represented at the following constraint:

B. Generator

There areMgenerators in a microgrid which consist of conventional power plants, distributed generation, new energy, etc.gm(t) denotes the amount of energy produced by generatormat time slott, wherem∈{0,1,...,M}, it has the following upper and lower bound constraint:

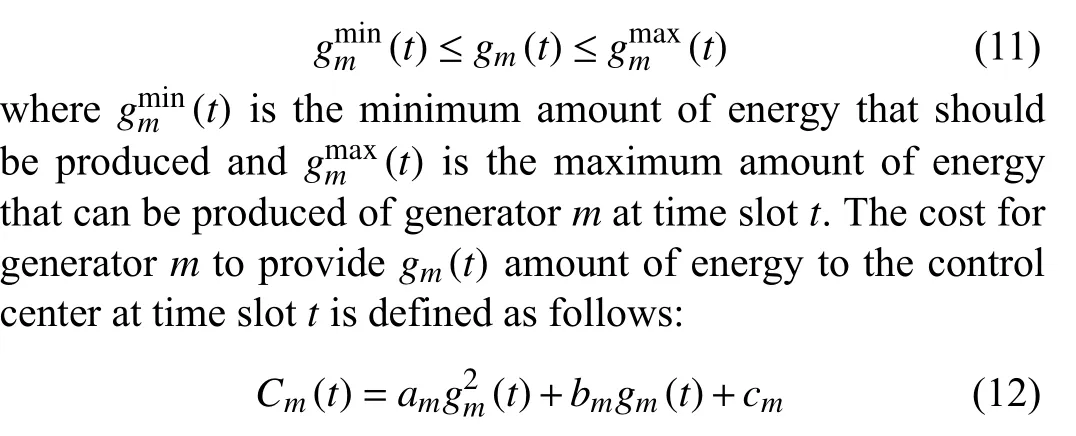
wheream,bmandcmare parameters of generatorm.

The power balance in the whole microgrid ensures that the amount of all the energy produced is the same as that of all the energy consumed at every time slot, which is represented as the following equality constraint:

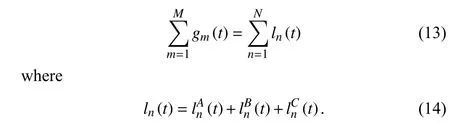
C. Control Center

The control center is the decision maker for the microgrid. It will choose suitable strategies to operate and manage the whole area and the strategies can be different patterns such as centralized approach, decentralized approach, distributed approach and so on, but the ultimate goal of all of them is to maximize the benefits of the users. In this paper, we design a fully distributed approach to optimal smart charging for users and optimal generating power for generators. First, at every time slott, the control center will declare the real-time electricity pricep(t), users will adjust their energy consumption plans considering the real-time electricity prices and their target energy consumption to maximize their benefits and satisfaction at the same time. In this process,users are independent of each other and they only solve their own optimization problems because there is no constraint between them. Then they will send back the amount of the energy requirement to the control center and the amount of gross generation will be decided according to the supply and demand matching. Finally, the control center will decide the amount of energy purchased from every generator according to the amount of gross generation. Generators are not independent of each other because there are constraints between them so the control center will use a distributed algorithm to decide the actually amount of energy generation of every generator to protect the privacy of the generators. In summary, the whole optimization process is distributed because users only have to provide the final information of energy requirement and generators only have to share information with their neighbors.

There are some notations:

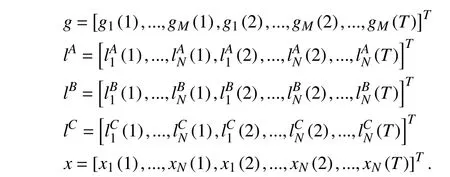
The optimization problem can be written as follows:

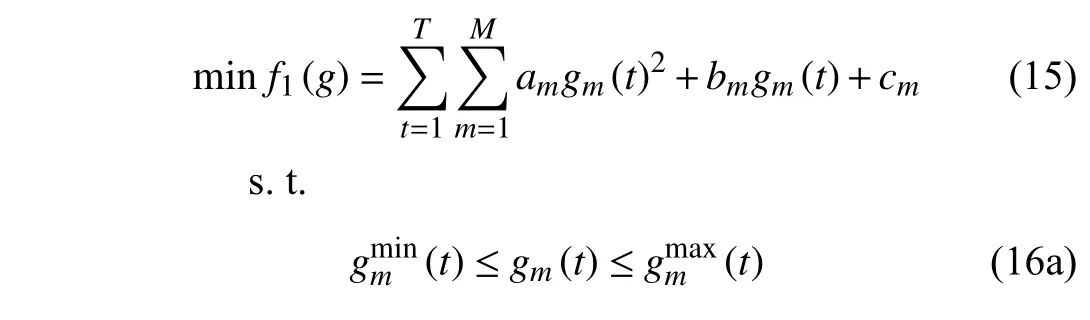
III. ALGORITHM DESCRIPTION AND CONVERGENCE ANALYSIS

A. A Novel Combined Neurodynamic Algorithm to Solve the Nonconvex Optimization Problem of Users

We first handle the problem (17) with constraints(18a)–(18g). We notice that the constraint (18g) is a mixed integer programming constraint and it is hard to deal with, so we convert it into the following constraints:

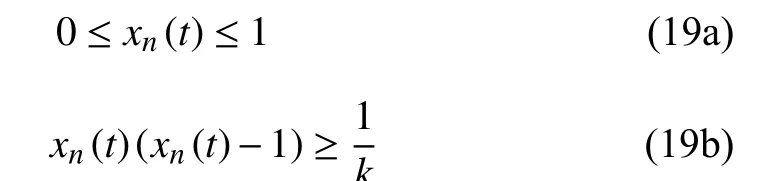
wherekis a constant and tends to infinity.

So, our optimization problem becomes (17) with constraints(18a)–(18f) and (19a)–(19b).

We assume that all the constraints including (18a)–(18f) and(19a)–(19b) are defined as follows:

whereIis the total number of constraints and

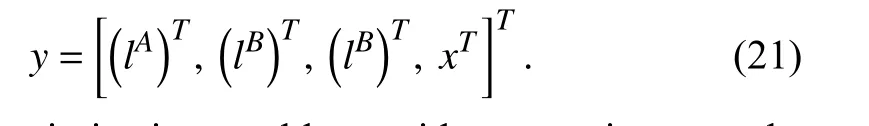
Then, our optimization problem with constraints can be converted into the following unconstrained optimization problem:

Thus, neural network (23) is asymptotically stable. ■

From Theorems 1 and 2, we can know that neural network(23) can converge to a local optimal solution with an arbitrary

Fig. 3. Flow chart of the combined algorithm.

B. Graph Theory

C. A Distributed Algorithm to Solve the Convex Optimization Problem of Generators

We handle the problem (15) with constraints (16a) and(16b).ln(t) can be calculated by the combined algorithm above and it can be seen as constant, so we can rewrite p roblem (15) into the following distributed form:

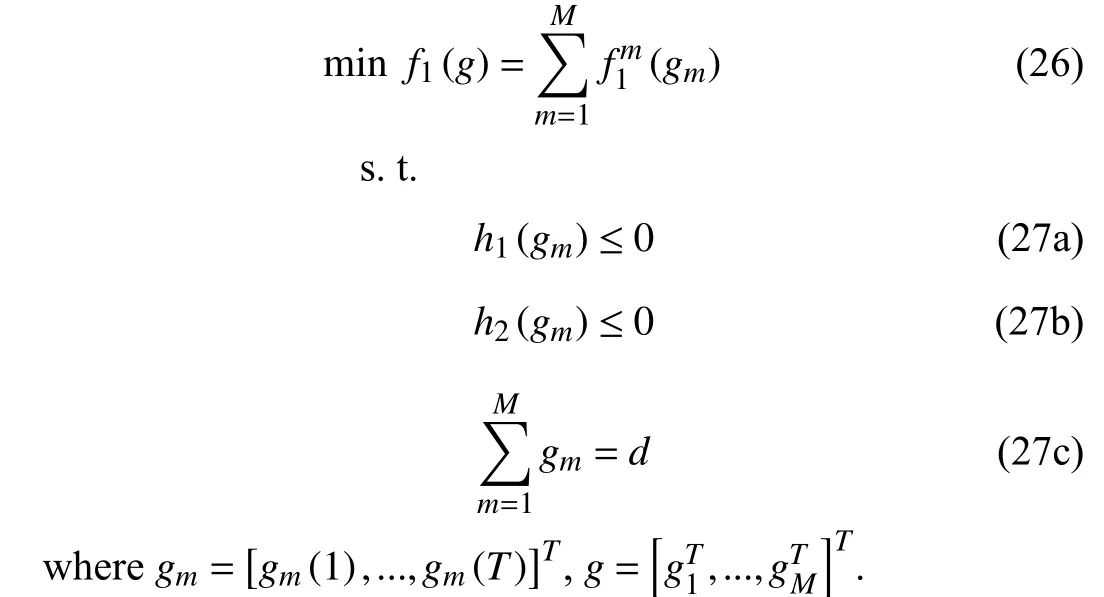
Problem (26) with constraints is equivalent to the following problem using the exact penalty function method:

From (28),f3(g) is convex and from (30), ∇f3(g) is upper semi-continuous with compact convex values, thenB(A) is also upper semi-continuous with compact convex values. So,there exists at least a local solution of (32) wheret∈[0,+∞)according to the local viability.

IV. SIMULATION RESULTS AND CONTRAST EXPERIMENTS

A. Simulation Result of the Optimization Problem of the Users

In this paper, we choose the experimental environment with 100 users, 5 generators and 5 time slots. First, we perform the simulation experiment of the users. The experimental data of one of the users are shown in Table I. Let α=40,ta=1,tl=5,Ea=20,El=20,lCmax=10 kW andC=50 kW, a local optimal solution to the problem (17) with all the constraints can be found using the gradient method (23). The results are shown in Figs. 4–6 which are the equilibrium points of the zero-one variables, the loadBand the loadCseparately.Afterwards, we use our combined neurodynamic algorithm trying to find the global optimal solution to the problem (17)

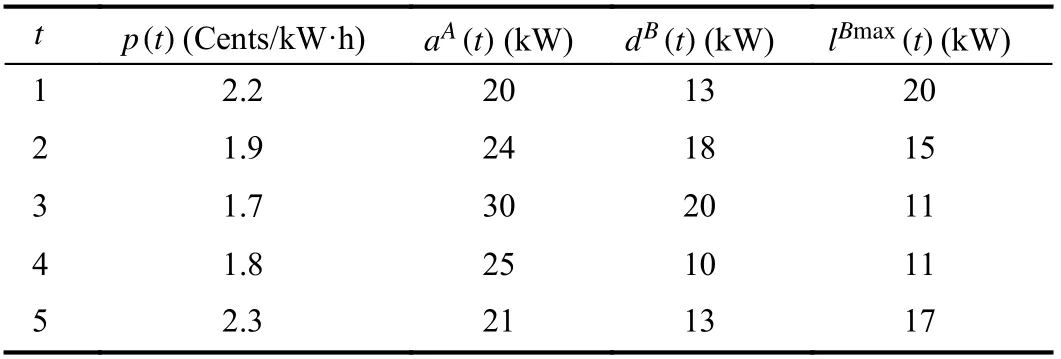
TABLE I EXPERIMENTAL DATA OF ONE OF THE USERS

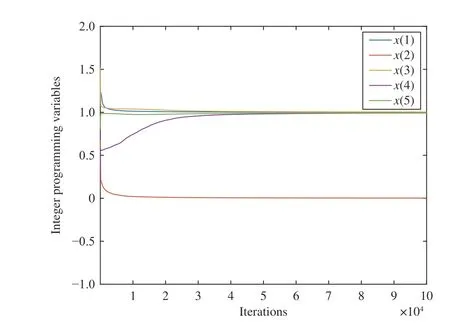
Fig. 4. The equilibrium point of the zero-one variables using the algorithm(23).

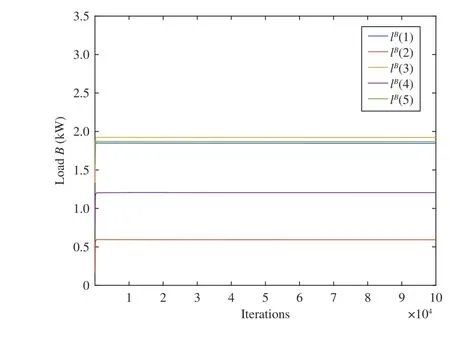
Fig. 5. The equilibrium point of the load B using the algorithm (23).

with all the constraints and the results are shown in Figs. 7–10.Fig. 7 shows that the value of the object function decreases and becomes stable eventually as the iteration progresses.Fig. 8 shows that the zero-one variables jump between 0 and 1 and become stable finally. Figs. 8 and 9 are the optimal solutions of loadBand loadC, respectively. We do the contrast experiment using the algorithm proposed in [26]which combines the neural network algorithm with the particle swarm optimization algorithm. The results can be seen in Figs. 11–14. By comparing the results of the two algorithms we can get that the optimal values of the object function are close but the optimal values of all the variables are different, this is because that it is difficult to find the global optimal solution of the nonconvex problem and we can only get a better and better solution by comparing different

Fig. 6. The equilibrium point of the load C using the algorithm (23).

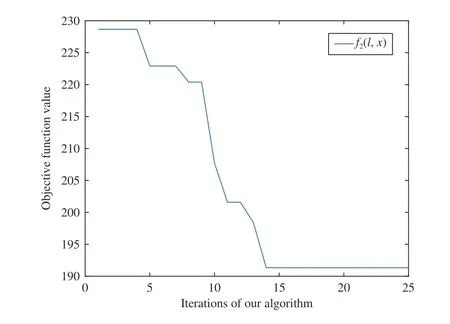
Fig. 7. The optimal value of the object function using our algorithm.

Fig. 8. The optimal values of the zero-one variables using our algorithm.

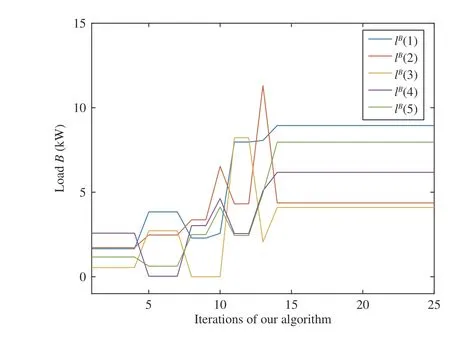
Fig. 9. The optimal amount of the power of the load B using our algorithm.

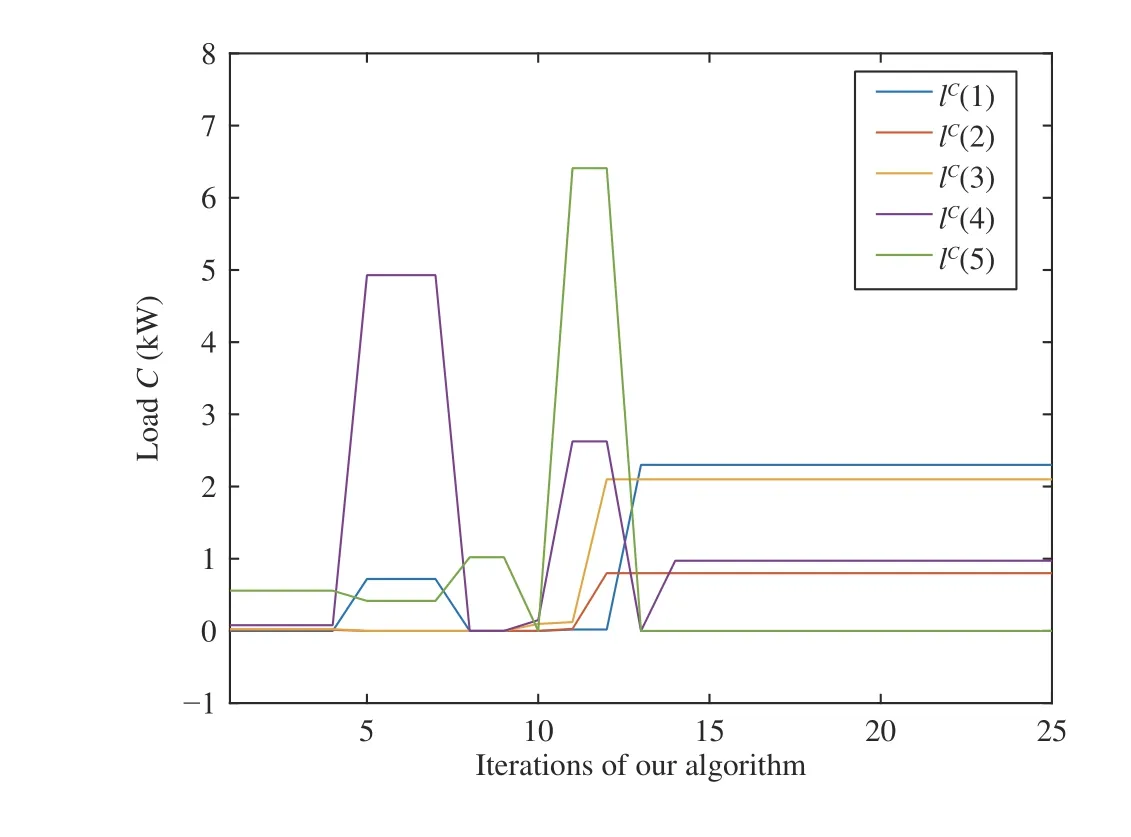
Fig. 10. The optimal amount of the power of the load C using our algorithm.

Fig. 11. The optimal value of the object function using another algorithm.

Fig. 12. The optimal values of the zero-one variables using another algorithm.

Fig. 13. The optimal amount of the power of the load B using another algorithm.

Fig. 14. The optimal amount of the power of the load C using another algorithm.

local optimal solutions constantly. What is more, our algorithm converges within 14 iterations while the contrast algorithm converges within 29 iterations. So, our algorithm has the advantage of faster convergence speed.

B. Simulation Result of the Optimization Problem of the Generators

We perform the simulation experiment of the generators.ln(t) has been calculated in the process above and we can getd=[3124,2756,3199,3215,2896]T. The experimental data of the generators in the first time period are shown in Table II.To protect the privacy of the generators, they can only exchange information with their neighbors, then the communication topology of the generators can be seen in Fig. 15. Obviously there exists a weight-balanced directed spanning tree. So, we can use the distributed algorithm (31) to find the optimal solution of the problem (15) with all the constraints and the result is shown in Fig. 16. We do the contrast experiment using the centralized algorithm proposed in [12] which uses the penalty method to deal with the constraints and the result is shown in Fig. 17. We can see that the equilibrium points using our distributed algorithm (31) are consistent with those using the centralized algorithm. The equilibrium points of the generated energy in the other four time slots using these two algorithms are shown in Figs. 18–21,respectively. We can see that the optimal solutions are same using these two algorithms at all time slots, which indicates that our distributed algorithm is effective. The advantage of our algorithms is that the generators deal with their own optimization problems in a distributed way and they only have to exchange information with their neighbors, so their privacy is protected to the greatest extent.

TABLE II EXPERIMENTAL DATA OF THE GENERATORS IN THE FIRST TIME SLOT

Fig. 15. Communication topology of the generators.

Fig. 16. The equilibrium point of the generated energy in the first time slot using the algorithm (31).

Fig. 17. The equilibrium point of the generated energy in the first time slot using another algorithm.

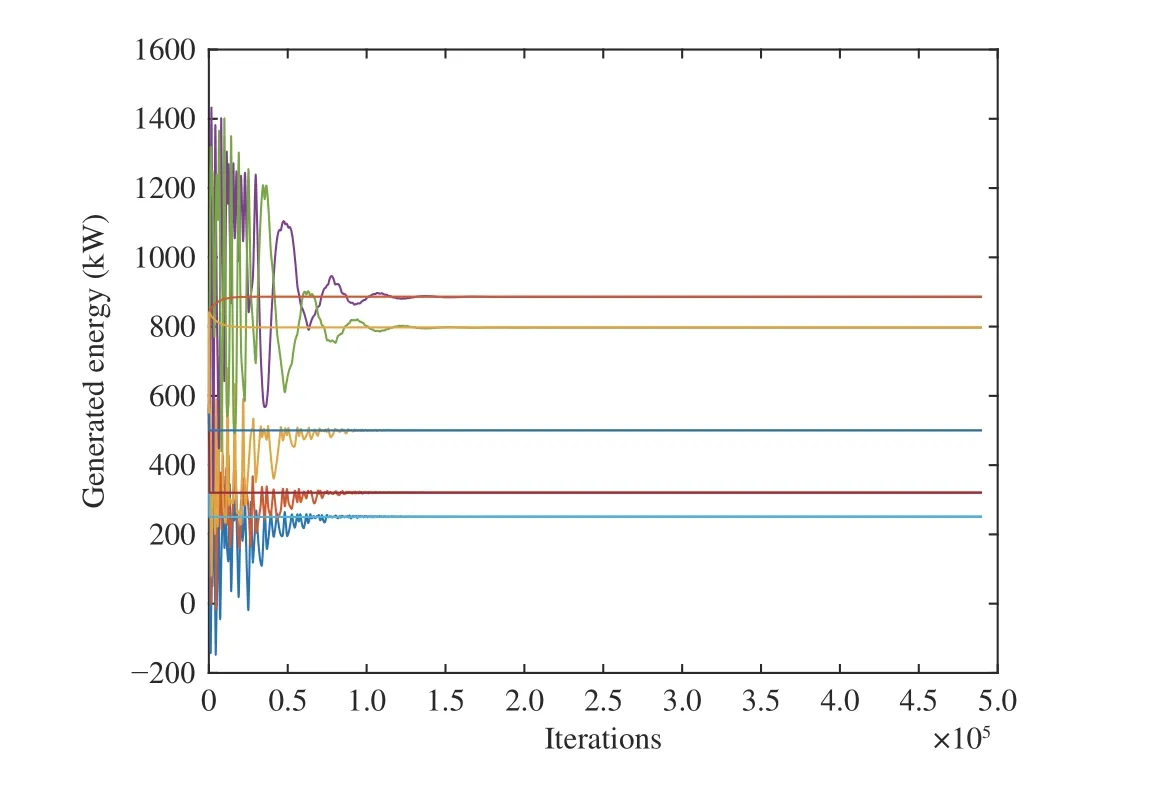
Fig. 18. The equilibrium point of the generated energy in the second time slot.

V. CONCLUSIONS

In this paper, we construct a microgrid model which

Fig. 19. The equilibrium point of the generated energy in the third time slot.

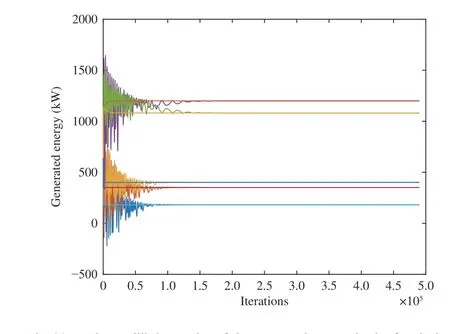
Fig. 20. The equilibrium point of the generated energy in the fourth time slot.

Fig. 21. The equilibrium point of the generated energy in the fifth time slot.

includes the optimization problems of the users and the generators at the same time. In the user side, two types of the load and the electric vehicles are considered where the zeroone variable is introduced to distinguish the two states of the electric vehicles. The users deal with their own optimization problems and the generators only exchange information with their neighbors, so it is a fully distributed microgrid model which can protect privacy of the uses and generators effectively. A novel neurodynamic algorithm which combines the neural network algorithm with the DE algorithm is put forward to deal with the nonconvex problem. The distributed algorithm using a new method to deal with the inequality constraints is used to solve the convex problem. The simulation results and contrast experiments show that our model and algorithms are effective.