稳健估计在地铁施工监测中的应用
韦子豪
(华北理工大学矿业工程学院,河北 唐山 063210)
0 引言
根据现代误差理论,从科研实验以及生产活动里收集的数据,其基础数据在输入空间数据平台的阶段,将出现不确定性,以及可能因为量测设备的固有精度、量测技术、实施方案等的局限性和差异性而引入不同程度的误差,粗差的出现是不可避免的。为了获得准确的变形监测解析数据,在数据的处理过程中需采取恰当的方法对粗差展开测定和筛除。粗差的处置一般能够划分成两类:一种是先把包含粗差的测量值运用统计检测的方法予以筛除,然后执行数据操作;第二种是把包含粗差的测量值视作方差反常,采取稳健估计方式予以处理,这是把粗差划分为随机模型,经过定权来清除粗差对测量结果造成干扰的一类办法。
传统最小二乘估计的手段由于难以排除粗差的干扰,产生了缺陷,不过稳健估计的手段可以凭借在数据中实施加权使得粗差信息的权值降低进而排除粗差带来的影响,从而让数据的稳定性增强,可以应对变形监测的要求。鉴于此,本文在对变形监测的数据进行处理时,运用稳健估计的方法,对其抗粗差特性进行深入探究,同时和常用的最小二乘法做出比较。
1 模型建立
1.1 一元线性回归分析原理及模型
实验牵涉到孔深和位移变化量两个参量,运用的回归模型属于一元线性回归模型[1]。这两个指标参量间的关系是经过求算一个参量的线性回归表达式来确认的,即是y=a+bx+v中a与b的数值。其中:x是孔深;y是位移变化量;v是y的更正数值;S是下沉量y的中误差;n是观察测定数值;a是回归方程常数项;b是回归方程的斜率。
由方程y=a+bx+v得:

数据的测定步骤是等权观测,经过最小二乘法求算出a、b的数值:

中误差:

1.2 稳健估计原理及方法
稳健估计是隶属于极大似然估计的一类特殊方式,可以确保所预估的参量不会受到粗差的干扰,其准则是有效运用测量数据当中的有效信息,删掉无效数据[2]。从客观使用阶段,无法精确知晓测定数据信息中的有用信息与其所占有的比例,因此从抗粗差的目的入手,需冒着降低效率的风险,去获得比较稳定且拥有实际效用的估计值。稳健估计一般包含了三种,主要是M-估计、L-估计与R-估计。首先,M-估计一般被解释为极大似然估计。主要是Huber参考早期出现的M-估计进行优化升级而产生。丹麦研究者Krarup等曾将稳健估计运用到测定领域。L-估计被称作排序线程组合预估。R-估计也被称作秩估计。本论文选择在测量界运用比较成熟普遍的M-估计展开数据处理与操作。
M-估计的方式有许多,运算方法近似于最小二乘法进行平差,其中便于程序实现的为选权迭代法[3],主要是按照回归残差的数值高低确认各位点的权重,给残差比较大的位点赋予较小的权重或者零权值,以减弱其对回归的干扰,实现稳健的目标。
权函数的确立属于稳健估计的核心。在测量阶段,测量误差表现为正态分布的特征,权函数则参考测定数据的残值情况而确定,对常规范围区段之内的较小残值赋上一般的权重,对比较大的残差稳健预估会减低此测量值的权重,或者在其残差过高时将此观测值的权重设置为零,由此达成去掉粗差的作用[4-6]。稳健估计属于一类特别的极大似然估计,稳健估计经过去除不利测定数值,间接地增大准确测定值权值的函数方法[7]。
稳健估计里存在一种重要的模型,即高斯—马尔可夫模型,详细如下:

其稳健估计准则如下:

在稳健预估过程中,对等权测定,权函数重点参考残值的情况来确定。在非等权观测阶段,关于稳健估计应配置的权重必须考量观测权重的干扰,在不等权观测里,若无需考量观测权重,一般取,但稳健估计就无法达到有效的抗差作用,对拥有稳健特性的权函数,在兼顾各个权iP的状况之下,其预估标准为:

如果观测值彼此不相关,则(1)~(5)式里,权函数对应的迭代模型可以归纳如下:
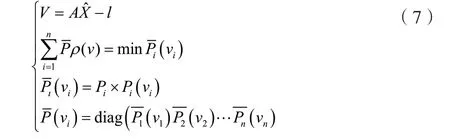
相应地,对于相关的观测值,此时稳健估计的权函数模型为:

2 实例分析
2.1 数据选取
为进一步了解本研究制定方案的有效性,现将深圳某地铁路段从建工点的基坑监测信息纳入检验,这一基地表现出从西往东高度递减的趋势,且为3个台地地形,其高程先后处在130 m、110 m、70 m~90 m,而地块当中相对高差大致在10 m~70 m。区域东南端属于废旧的竹坑水库,经测量,水面高程大致在65 m;但西侧边坡要求挖深降低高程,最大高度差约为49 m。本文数据是由CX-3C型基坑测斜仪采集得到的,本实验选取第19期的前16组数据进行分析,如表1所示,经过验证,该数据不含粗差。在使用最小二乘法的前提下,结合稳健估计的方法,就其回归函数实施系数运算,评估后几组的移动变化情况。先后探讨具备粗差以及不存在粗差的情况下,两类方式的精确性。
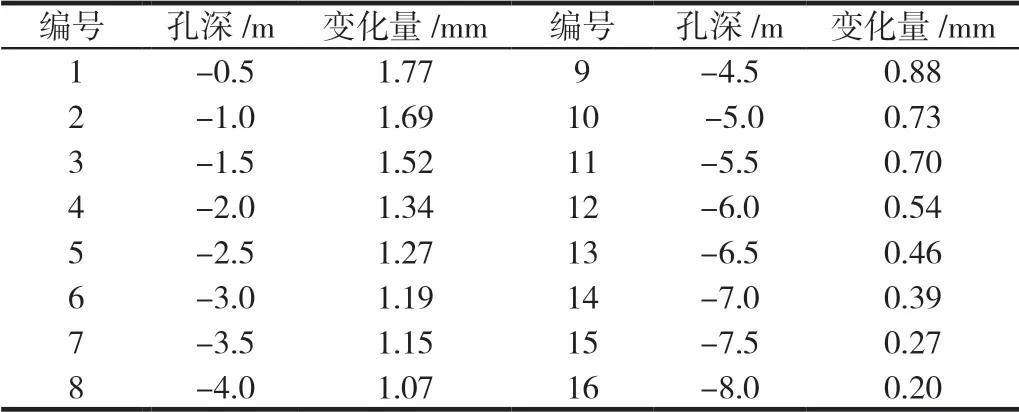
表1 原始监测数据
2.2 实验分析
为对比最小二乘法与稳健估计在变形观测项目数据处理中的差异,通过编写Matlab代码执行最小二乘法与稳健估计步骤的操作,进行程序实现,对两者精度展开对比。同时,当观测数据中存在粗差时,比较稳健估计法与最小二乘法的抗差性,由此体现稳健估计对粗差的抗干扰能力。
2.2.1 在不含粗差的情况下
在不包含粗差的状况下,残差图如图1所示,对回归方程的系数依次运用最小二乘法和稳健估计的方式求算,同时获得对应的回归表达式,并展开比较。
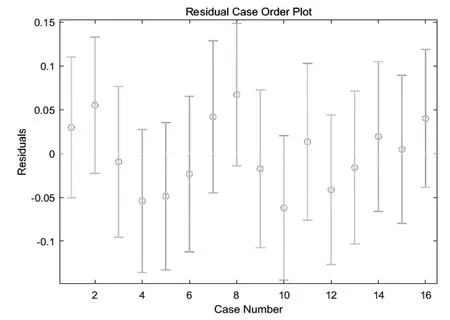
图1 不含粗差情况下得到的残差图
经过最小二乘法求出的方程系数为a1=1.8403, b1=-0.2099,因此回归表达式为:
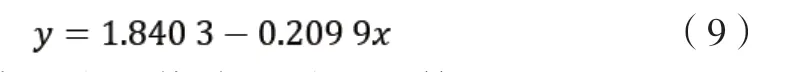
基于此,借助稳健估计的手段运算出a2=1.8463, b2=-0.2107,对应回归方程如下:
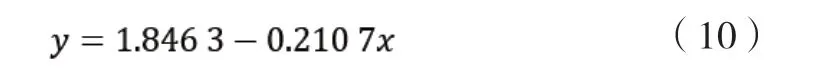
通过两个表达式的形式,对于不存在粗差的状况,以上两类方法获取的结果基本相同,通过Matlab画出两者的函数曲线如图2所示,可以看到两条直线基本重合。比较两类算法获得的中误差,最小二乘法运算所获得的结果中误差S1=0.4997,稳健估计运算的结果中误差S2=0.5016,发现在不包含粗差的状况下,最小二乘法和稳健估计所获得的结果与精度都比较接近。
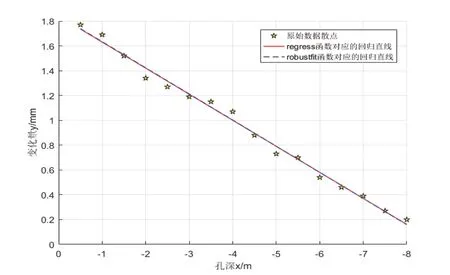
图2 不含粗差情况下最小二乘法与稳健估计的对比图
2.2.2 在含粗差的情况下
为了验证稳健估计的抗差性,将原始数据中第7组的数据位移变化量改为1.65 mm,增加粗差之后结果如表2所示。
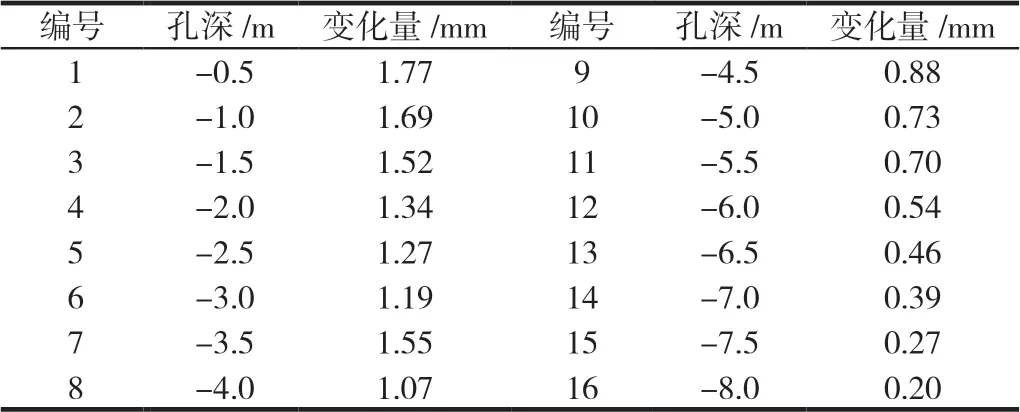
表2 加入粗差后的监测数据
所获得的残差图如图3所示,经过最小二乘法求算对应方程系数,可得 a3= 1.8903,b3= -0.2143,得到对应的回归方程为:
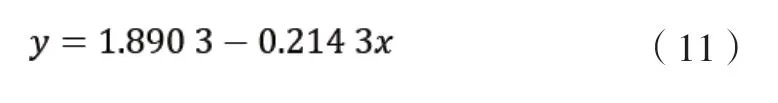
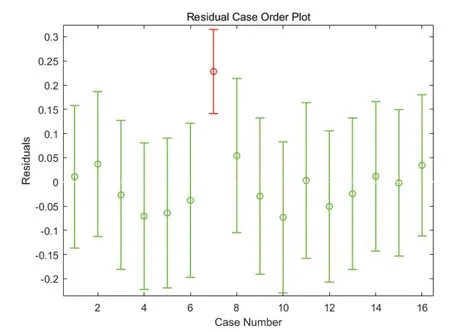
图3 在含有粗差的情况下得到的残差图
基于此,借助稳健估计回归研究存在粗差的数据,从中获取方程系数a4=1.8463,b4=-0.2107,则对应的一元线性方程如下:
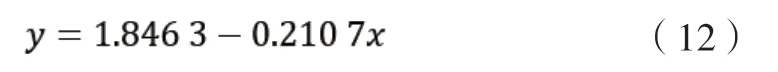
在没有粗差的情况下,最小二乘的方法与稳健回归的方法产生的回归模型相对一致,但在具有粗差的情况下,两类方式产生的回归模型存在非常明显的差异。借助图像能够了解到,最小二乘法产生的回归方程出现了往粗差值贴近的现象,但是稳健回归下具有更显著的抗差性。
经过把这两类算法所获得的方程图像绘制在同一幅图上如图4所示,可知两类算法获得的方程图像产生了显著的偏离状况,伴随孔深的增长,变化量之间的偏差也愈来愈大[8-9]。
对比两种运算方法获取的中误差,S3=0.5302为通过最小二乘法计算的中误差值,S4=0.5016为通过稳健估计计算的中误差值。对比发现,在监测数据含有粗差时,最小二乘法将粗差进行引入,平差结果不能反映真实情况,而稳健估计法能合理地将粗差剔除,在精确度和可靠性上均好于最小二乘法。
3 结论
1)本研究借助稳健估计以及最小二乘法,就样本基坑的监测数据实施了多项型曲线拟合,从中开展对实测数据的预估。基于两类方法的平差情况,不存在粗差时,稳健回归方法和最小二乘法在结果和精确度上比较接近,但最小二乘法实施起来相对简便。而如果观测数据中存在粗差,最小二乘法会产生粗差引入的问题,导致平差结果无法体现客观数据,稳健估计可以有效应对粗差在平差系统的影响,解析算法则展现出良好的抗差性,合理利用有效信息,不管从精确度还是从结果的可靠性上均要好于最小二乘法。
2)在真实的测量工作过程中粗差是不可避免的误差,能够选取稳健估计的办法对这类粗差进行去除,进而获得更为精确的数据结果。同时,在监测环境受限的情况下,运用稳健估计的平差方法也可以对数据进行较为准确的预测。

