基于GA-BP方法的地铁站动态人员冷负荷预测研究

杨 福，王衍金，江战红

（1.华东交通大学土木建筑学院，江西 南昌330013；2.南昌轨道交通集团有限公司，江西 南昌330038）

随着城市轨道交通需求的迅速扩大，地铁已经成为现代城市不可或缺的公共交通方式，极大地缓解了地面交通压力，方便了人们出行。乘坐地铁不但方便快捷，而且是一种绿色环保的公共交通出行方式。然而，高能耗也是地铁站运营过程中面临的实际问题，当前地铁站通风空调系统一般按照最大负荷需求进行设计，且很大一部分地铁站的通风空调系统在运行过程中并未根据站内人流量的变化进行实时调节，导致地铁站通风空调系统设备负荷率低，系统能效比远低于设计值，能源利用效率低[1]。近年来地铁实际运营数据显示，地铁站全年空调能耗约占其全年总能耗的31%[2]。降低地铁站通风空调系统能耗是降低地铁站运行能耗的重要途径。

由于地铁站不同时段人流量变化较大，导致通风空调系统负荷的波动，人流高峰时段和低峰时段相差甚大。要对地铁站通风空调系统采取运行调节措施，降低运行能耗，就必须对地铁内人流量及人员冷负荷进行预测。建立准确可靠的人流量预测模型，对站内的人员冷负荷进行计算分析，可为通风空调系统的运行调节提供重要的数据支撑。

当前冷负荷系数法是人员冷负荷计算的主要方法[3]，该方法把得热计算和负荷计算两步合并成一步，通过冷负荷系数直接从各种扰量源求得分项逐时冷负荷。然而由于地铁站深处地下，其围护结构内表面温度日逐时变化较小，人流量存在较大的波动性，且从室外进入地铁站内时的散热散湿状况较为复杂，本文在对地铁站人流量进行预测的基础上，采用人体散热模型进行人员冷负荷的预测计算。

1 GA-BP神经网络方法

1.1 传统BP神经网络方法

地铁站人流量分析和预测不但是地铁规划设计的基础，也是地铁运营公司和学者们关注的重点，学者们也提出了一些人流量预测模型，比如时间序列分析模型（ARMA，ARIMA）[4-5]、灰色预测模型[6]等。然而，对地铁站动态人流量的预测分析，这些方法存在一定的局限性，不具备自学习和泛化能力，预测精度也比较低，难以得到理想的预测结果。随着人工神经网络预测方法的兴起，如BP神经网络[7-8]、支持向量机[9]等模型的应用很好地解决了自学习和泛化能力的问题。在预测方面，BP神经网络法可以实现复杂的非线性问题，正是这种特点，使得BP神经网络法成为当前主要的预测方法之一。

1.2 GA-BP预测模型

虽然BP神经网络应用广泛，但也存在不足。传统的BP神经网络法初始权值随机赋值，容易使网络陷入局部极小，导致全局达不到最优[10]，这个问题使得传统的BP神经网络模型无法对地铁站人流量进行准确稳定的预测分析。针对该问题，采用遗传算法优化BP神经网络（GA-BP）对地铁站人流量进行预测分析，通过遗传算法得到最优初始权值和阈值并将其输入到BP神经网络中。

遗传算法用于优化BP神经网络的初始权值和阈值，根据建立的BP神经网络的初始权值和阈值，用训练数据训练BP神经网络，得到预测的输出值，计算预测输出和期望输出之间的误差，将误差绝对值之和作为个体适应度值F[11]

式中：n为网络输出节点数；yi为BP神经网络第i个节点的期望输出；oi为第i个节点的预测输出；k为系数。

个体的选择基于适应度比例的选择方法，每个个体的选择概率pi为

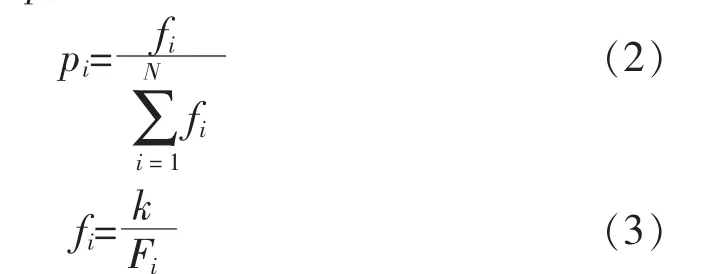
式中：Fi为个体i的适应度值，根据研究内容，适应度值越小越好，所以个体被选择概率与适应度值成反比；k为系数；N为种群个体数目。

2 人员冷负荷计算模型

人体与周围环境的换热是自然对流换热、受迫对流换热、辐射换热以及潜热换热共同作用的结果，受体表温度[12]、环境温度、空气流速以及风向的影响[13]。当风速较小时以自然对流为主，风速较大时以受迫对流为主[14-16]。由于地铁站处于地下，围护结构内表面温度逐时变化较小，人体与围护结构内表面的辐射换热量转化的冷负荷可忽略不计。研究表明，简化人体的几何形状对人体与环境之间的整体热传递影响不大[17]。一个身高约为1.7 m，体重约为60 kg的成年男子，其外表面积约为1.69 m2，为简化人体与环境的复杂换热过程，本文将人体简化为一个高1.7 m，底面直径为0.3 m的光滑圆柱，且人体表面温度均匀。

2.1 人体表面受迫对流换热

当人体周围空气流速较大时，人体表面以受迫对流换热为主，当风速大于0.75 m/s时，人体表面自然对流的影响可忽略不计[13]。人体表面受迫对流受环境风速、风向以及湍流强度的影响[18]

式中：N u为努谢尔特数；下标0表示湍流强度I为0%时的值；B为常系数；ReT为湍流能量产生和消耗的比率，ReT=I×Re0.5；Re为雷诺数，Re=lv/v；v为人体周围空气流速，m/s。

式中：I为湍流强度，反映脉动风速的相对强度；v′为风速的标准偏差；V为平均风速。

N u的定义

式中：h为对流换热系数，W/（m2·k）；l为定型尺寸；λ为导热系数，W/（m·k）。

将式（6）代入式（4）得

式中：A，n为常系数，根据实验数据所得[18]，A=9.93，B=1.03，n=0.54。

人体表面受迫对流换热量Qx为

式中：AD为人体外表面积。

综合式（8）和式（11）可知，地铁站人员与环境对流换热量形成的逐时冷负荷Q1为

式中：nτ为逐时人流量。

2.2 人体呼吸散热

人体呼吸散热包含呼吸显热散热和呼吸潜热散热两部分[19-20]

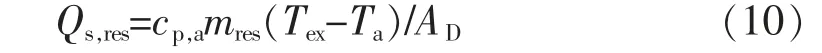
式中：Qs，res为呼吸显热散热；mres为呼吸质量流量；Tex为呼出空气温度；Ta为周围环境空气温度。

式中：dex为呼出空气含湿量；da为周围环境空气含湿量；hfg为水的汽化潜热。

2.3 人体皮肤表面蒸发潜热换热

人体皮肤表面蒸发潜热换热包含皮肤扩散蒸发散热，皮肤汗液蒸发散热[19-20]

式中：Qe，dif为皮肤扩散蒸发散热；Qe，rsw为皮肤汗液蒸发散热。

式中：wrsw为由调节性出汗引起的皮肤湿润度；Qe，sk为皮肤表面蒸发散热；w为皮肤表面湿润度[21]；Qe，max为人体表面最大蒸发量，其取决于皮肤和周围环境的水蒸气压力之差。

式中：Psk，s为皮肤表面的水蒸气分压力；Pa为环境空气水蒸气分压力；Re，t为服装与环境之间的蒸发热阻[22]。

综合式（9）、式（12）和式（19），地铁站人员逐时冷负荷Q为

3 结果验证与分析

采用Matlab编程对地铁站动态人员冷负荷进行预测。由于地铁站人流量的逐时变化，人员冷负荷也是动态变化的；因此对地铁站内的全天逐时人流量和人员冷负荷进行预测计算。选用南昌地铁1号线双港站和地铁大厦站2016年和2017年6月至8月的日逐时人流数据作为训练输入和验证数据，双港站是起始站，地铁大厦站是中转站。取2016年6月和7月的数据作为训练集输入数据，2017年6月和7月的数据作为训练集输出数据，将2016年和2017年8月的数据进行仿真检测网络的预测准确度。地铁营运时间为6：00至23：00，输入神经元数目为18，隐含层数为12，输出神经元数目为18，通过M atlab中的trainlm函数对网络进行训练。

遗传算法优化后的BP神经网络初始参数为种群规模100，进化代数500，权值和阈值的取值范围为[-3，3]。

利用遗传算法优化BP神经网络确定其最优权值wij，wjk和阈值θj，2个地铁站的平均适应度值在前期进化时不断降低，经过第261代的进化后，平均适应度值趋于稳定，稳定在147，而地铁大厦站，在进化了153代后，平均适应度值趋于平稳，稳定在178，此时的权值和阈值即为最优初始权值和阈值。

将优化后的最优初始权值和阈值输入到BP神经网络中进行训练，将得到的预测人流量与实际监测人流量值进行比较。图1和图2为GA-BP方法与传统的BP神经网络法及实际监测人流量日逐时人流量的比较结果。将得到的人流量预测结果代入人员冷负荷计算模型中，得出的人员冷负荷结果与实际监测人流量与人员冷负荷值进行比较。图3和图4是本文提出的GA-BP方法与传统的BP神经网络法及实际监测人流量日逐时人员冷负荷值的比较结果。

图1 双港站日逐时人流量对比结果Fig.1 Comparisons of the hourly passenger flow in the Shuanggang Station

图2 地铁大厦站日逐时人流量对比结果Fig.2 Comparisons of the hourly passenger flow in the Metro Central Station

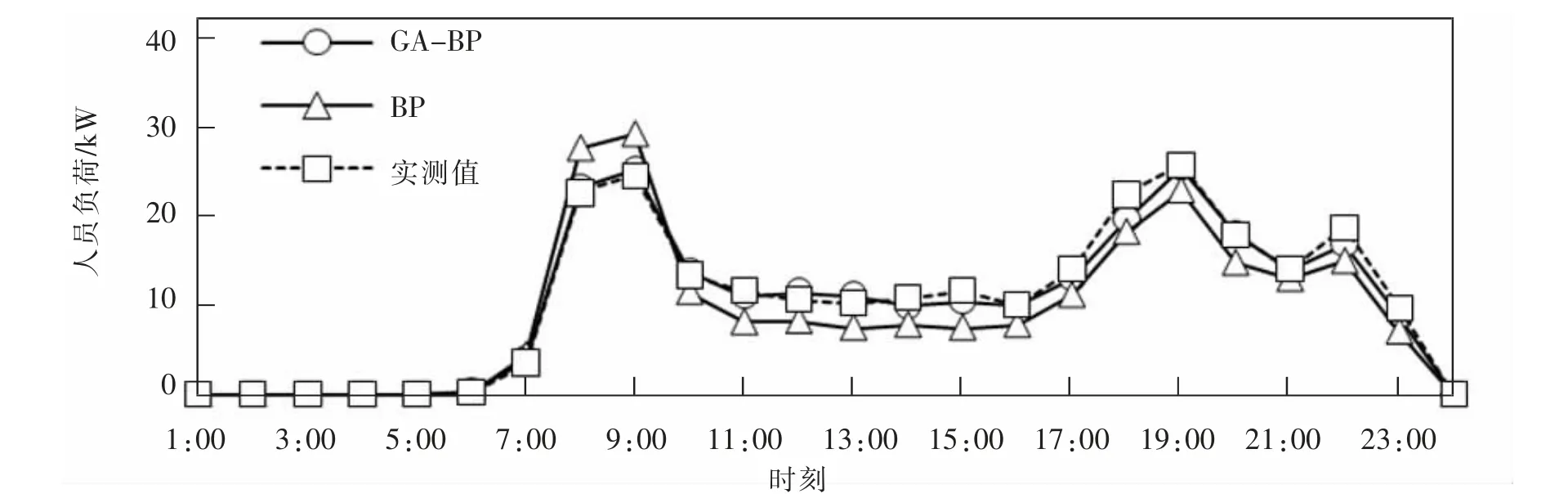
图3 双港站日逐时人员冷负荷对比结果Fig.3 Comparisons of the hourly personnel cooling load in the Shuanggang Station

图4 地铁大厦站日逐时人员冷负荷对比结果Fig.4 Comparisons of the hourly personnel cooling load in the Metro Central Station

比较可知，在双港站和地铁大厦站日逐时人员冷负荷值预测结果中，GA-BP模型和BP模型所得逐时预测结果均接近实测结果，而GA-BP模型的预测结果误差较小。GA-BP模型与BP模型误差比较如表1所示。

通过比较可知，双港站和地铁大厦站的GABP模型所得预测结果都明显更接近实测结果，相比于传统BP模型，GA-BP模型预测结果更稳定，波动幅度较小，预测误差降低10%左右。对比双港站和地铁大厦站，GA-BP模型的预测结果表明，地铁大厦站的预测误差比双港站偏大6.59%，其原因是地铁大厦站是中转站，客流量较大，且每日逐时人数波动较大，导致人员冷负荷波动大，预测准确度降低。

在人员冷负荷预测结果的分析过程中，本文采用拟合相关系数指标R2评价每日逐时人员冷负荷预测准确度，通过计算每日逐时预测值曲线与实际值曲线的拟合程度来评价预测算法的拟合能力，R2越接近于1，则代表拟合程度越高，预测准确性越好。

表1 逐时人员冷负荷预测结果平均误差对比Tab.1 Comparative results of the hourly personnel cooling load average error for the prediction models%

分别就GA-BP方法和BP神经网络方法对人员冷负荷预测结果的拟合相关系数进行了比较，结果如图5和图6所示。

图5 双港站人员冷负荷拟合相关系数对比Fig.5 Comparison of the fitting correlation coefficients for the personnel cooling load in the Shuanggang Station

图6 地铁大厦站人员冷负荷拟合相关系数对比Fig.6 Comparison of the fitting correlation coefficients for the personnel cooling load in the Metro Central Station

比较结果可知，2个地铁站的GA-BP模型对人员冷负荷预测的拟合相关系数较为稳定，而传统BP模型的拟合相关系数波动较大，仅有部分日期的拟合相关系数较接近1.0。由此可见传统BP模型人员冷负荷预测结果偏差更大，且人员冷负荷预测结果波动较大。双港站的预测结果显示，相比于传统BP预测模型，GA-BP模型拟合相关系数R2更接近1.0，平均值为0.924 6，而BP模型的拟合相关系数平均值为0.823 9。地铁大厦站GA-BP模型拟合相关系数平均值为0.891 7，而BP模型的拟合系数平均值为0.874 3，说明GA-BP预测模型比BP模型更准确，优化效果明显。图7是双港站和地铁大厦站的拟合相关系数比较结果，地铁大厦站的人员冷负荷拟合度比双港站低，拟合相关系数平均值低0.032 9，且6，9，20 d和27 d的拟合系数值偏差较大。由于地铁大厦站是中转站，日逐时人数波动较大，导致人员冷负荷波动较大，拟合度降低；因此地铁大厦站的预测结果偏差比双港站大。

图7 两站人员冷负荷拟合相关系数对比Fig.7 Comparison of the fitting correlation coefficients for the personnel cooling load in the two stations

综上所述，GA-BP模型比传统的BP模型预测效果更好，预测准确性更高。但是，GA-BP模型的预测误差仍然在10%左右，主要原因是地铁站人数波动较大，人员冷负荷处于动态变化当中，难以得到更加准确的网络模型；虽然大部分日期的逐时人员冷负荷拟合程度较好，但是仍然有部分日期的R2值偏低，在9 d和25 d后的R2值降低幅度较大，原因是人数变化太大，导致人员冷负荷波动较大，预测准确度降低。尽管在人员波动较大时GA-BP模型的预测结果仍存在偏差，但相比于传统的BP神经网络模型更加准确，且稳定性更佳，更加适用于地铁站人员冷负荷的预测分析。

4 结论

地铁站人员冷负荷的预测对于地铁站通风空调系统的节能运行有重要意义，建立了地铁站人员冷负荷计算模型，并采用遗传算法优化的BP神经网络对地铁站的人流量和人员冷负荷进行了预测，得出以下结论。

1）利用遗传算法对BP神经网络的初始权值和阈值进行优化，提高了BP神经网络的非线性学习能力。通过与地铁站实际运行监测结果和传统BP神经网络模型的预测结果比较发现，GA-BP模型的人员冷负荷预测平均误差降低10%左右。

2）由于地铁大厦站是中转站，人流量相对双港站较大，导致人员冷负荷波动大，对比结果表明，地铁大厦站预测误差比双港站大6.59%。

3）对比BP神经网络模型，两站人员冷负荷GA-BP预测模型结果的拟合相关系数值至少提高了0.1，且预测稳定性更佳，更加适用于地铁人员冷负荷的预测。