开展“一题一课”,追求“少慢精深”
朱月凤


我国著名数学家李大潜院士在复旦大学数学科学学院新生迎新大会上的讲话中提到学好数学要做到“少慢精深”,而不是刷题式的贪多求快。笔者在中考复习备考期间以“一题一课”进行解题教学,积极实践李院士提出的“少慢精深”数学学习理念,取得较好的教学效果。笔者结合本地区一道新定义几何中考题开展“一题一课”教学,现将教学过程整理成文,并阐释教学立意。
一、考题呈现及说明
定义:我们知道,三角形的内心是三条角平分线的交点。过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形,若有一个图形与原三角形相似,则把这条线段叫作这个三角形的“内似线”。
(1)等边三角形“内似线”的条数为 ;
(2)如图1,△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求证:BD是△ABC的“内似线”;
(3)在Rt△ABC中,∠C=90°,AC=4,BC=3,点E、F分别在边AC、BC上,且EF是△ABC的“内似线”,求EF的长。
说明:这是2017年的南通中考第27题,不少学生在问题求解时遇到困难,有些是构图不当,有些是缺少一些铺垫式问题的辅助思考,没有顺利贯通思路,笔者决定通过“一题一课”的形式来帮助学生掌握这类问题的求解方法。
二、“一题一课”教学过程
教学环节一:引例热身
引例1:思考与直角三角形内心有关的问题。
1.在Rt△ABC中,∠C=90°,请你说说怎样找到△ABC的内心。
2.在Rt△ABC中,∠C=90°,AC=4,BC=3,围绕△ABC的内心,你能得到哪些结论?
预设:直角三角形的两直角边是3和4,则内心到三边的距离是1。通过开放式问题,复习三角形内心的概念,寻找三角形内心的途径以及与三角形内心有关的结论。
设计意图:引例1起到热身的目的,组织学生有效复习了直角三角形的内心,然后特殊化为“3,4,5”的直角三角形。学生通过议论、对话和交流,对这个图形下的性质有较为全面的认识和思考。
引例2:如图2,在Rt△ABC中,∠C=90°,AC=4,BC=3,D是边AC上一点,且满足AD=3,你能在边AB上找一点E,使得△ADE与△ABC相似吗?
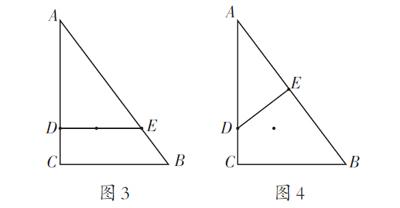
教学记录:如图3、图4,请学生到前面来展示作图方法,说说具体作法,写写相似,强调对应,总结模型。
在学生画出图3、图4之后,先围绕图3这种基本图形(“A型”相似),可预设以下问题:如图3,在这个基本图形中,DE与BC在位置上有什么样的关系?DE与BC之间的距离是多少?内心O到边BC的距离是多少?线段DE经过内心O吗?你能求出DE的长度吗?(以上系列“问题串”可以渐次呈现,可结合学情相机给出,如果学情很好,还可鼓励学生自主提出一些问题。)
接着再引导学生观察图4,围绕图4这种基本图形(“反A型”相似),预设以下问题:如图4,你能求出DE的长度吗?
在此基础上,将图4中DE所在的直线向下平移(如图5),使其经过△ABC的内心,与边AC、BC所在的直线分别交于D'、E'。引导学生思考:点D'在边AC上吗?若在,求出D' E'的长度。
解后反思:对比图3和图5中的DE与D' E',这两条线段具有哪些共同特征?
教学意图:引导学生回顾三角形相似的知识,渗透A型与反A型相似的印象,为后面新问题的分类讨论以及如何求内似线的长度设好铺垫。围绕基本图形,进行一系列的变式研究,特别是对经过内心的直线截三角形两边得到的三角形与原三角形相似时,如何分析对应边之比,并利用相似比求出相应线段的长度,这样的问题经过充分探究之后,可以对本课将要研究的新定义考题的最后一问达成较好的铺垫作用,实现铺平垫稳的设计目标。
教学环节二:考题讲评
呈现2017年南通中考第27题,删除基础问,只保留第(3)问。
教学过程:学生独立思考5分钟后,围绕题意,请同学们谈谈对已知条件有什么样的认识;受到“引例2”中求D' E'长度的启示,看看可以从哪里着手解决此题。尝试添加辅助线。接下来进行思路突破与解法交流。限于篇幅,不再给出具体的解法示意。
学生讲评之后,进行必要的小结或解后反思,提炼一些关键步骤,然后安排相关学生复述(“再说一遍”)。最后可给出一道变式拓展题如下:
【拓展思考】该直角三角形中,你能找到几条内似线?都能求出它们的长度吗?
教学过程:针对2017年南通中考新定义考题的第(3)问,学生独立思考之后,快速获得思路的学生先在小组内交流讨论,然后大组汇报,在进展到关键步骤时,教师让其他学生复述思路,这样可以让更多的学生的思维被充分卷入解题思路中。
三、教学立意的进一步阐释
第一,较难题教学备课要追求深度思考。
每份练习都有少数较难题,教师往往把课堂教学时间花在这些较难题上,但是讲评后却总感觉效果不好,仍然只有少数优秀学生能跟得上讲评节奏。这时,教师可反思讲评的用力点是否精准,如果按照所谓参考答案的解答方式“顺流而下”,可能就是备课的功夫不足,没有想清辨明备课用力点。我们认为,教师在讲评这些较难题之前,自己要对考题的关键步骤、主要难点、易错点想清悟透,然后针对这些关键步骤、主要难点或学生可能的障碍预设一些教学环节进行难点突破。比如上文的课例中,我们设计了两个“引例”,就帮助了更多学生进行“热身训练”,再出示那道较难题时,学生就能获得思路启示,进而快速想到思路并解答成功。
第二,较难题教学要重视关键步骤处理。
教师在较难题教学时要十分重视一些关键步骤的处理,比如充分解读题意,特别是针对本文课例中关注到的新定义问题,可先引导学生深入理解新定义的本质或内涵,必要时要让学生画图并结合图形在小组内交流各自对新定义本质的理解,然后再迎难而上,各个击破。在碰到较难题时,组织学生善于排除干扰,分析并“暴露”出问题的求解目标,有时这种“暴露”目标的解析工作也是解题征途中的关键步骤,要让学生学会这种解题技术。还有,在处理某些关键步骤时,可能会遇到对一些经典问题或拓展变式的处理,这时如果学生没有能及时想到这些经典问题或拓展变式的解法思路,教师可通过必要的铺垫式问题(如本文课例的兩个“引例”),让学生先做好必要的热身复习,再迎难而上,往往就能顺利地攻克较难题。学生经历这样的解题教学过程,不但能解出这一道较难题,而且能悟出今后如何分析较难题。这也就是实现了从“授人以鱼”到“授人以渔”的教学追求。
(作者单位:江苏省海安市城南实验中学)
本文系江苏省南通市规划办“十三五”课题“‘学材再建构的初中数学课例研究”(编号:2020007)阶段性研究成果。

