基于外部观测温度的锂离子电池电极温度在线实时预测系统

高岩飞，毋青松，宫汝燕，黄雪涛，富文军

1.山东交通学院 汽车工程学院，山东 济南 250357； 2.威海市产品质量标准计量检验研究院，山东 威海 264200

0 引言

动力电池作为电动汽车的重要动力装置，其性能直接影响电动汽车的动力性、经济性和安全性。锂离子电池单体工作电压高，循环寿命长，功率密度和能量密度高，已成为电动汽车动力电池的主要选择[1-5]。动力电池受其内部材料化学特性影响，工作时对外界环境温度较为敏感[6]：温度过高，电池副反应和性能衰减加快，电池使用寿命降低；温度过低，电池内阻增大，释放功率和容量均大幅降低，电池容量发生不可逆衰减[7-8]。动力电池在高负荷工况下运行、过充过放或内部短路等不确定情况下，短时间内积聚大量热量，若未及时散发，动力电池有可能严重受损[9-13]。电动汽车动力电池组合是将多个电池单体通过封装、装配组合而成，最小单元是锂离子电池单体，直接、有效地观测、估算锂电池单体内部温度，有助于开发动力电池组合的“电池材料-壳体”精确均衡热管理系统。

在电池生产过程中通过内置温度传感器测量电池内部温度有较大局限性[14]。一般来说，锂离子电池根据热模型预测温度。锂电池温度场热模型是典型的时间空间耦合的分布参数系统，模型比较复杂，计算量大，很难直接在线实时预测[15]，需对热模型降阶处理，或简化电池结构，忽略对热模型影响较小的因素，提高计算速度，但精度有所下降[16]。文献[17]建立锂离子动力电池温度场热物理模型，通过采集电池箱内壁温度和冷却液温度，在线实时准确预测锂电池表面电极处的温度。文献[18]针对电池内阻随电池劣化程度改变的特性，采用基于经典热传导理论的锂离子动力电池离散化热模型进行动态估算，解决了圆柱型电池核心温度的在线估算问题。文献[19]提出一种电池内部温度场的传递函数估算方法，实时计算电池内部温度场。文献[20-22]分别建立了锂离子动力电池的三维热模型，并通过恒流充放电试验对电池内部温度进行精确估算和可靠性研究。

本文将电池电极温度作为外部观测温度，近似代替电池内部电极的实际温度，以期实现锂离子电池内部电极温度的在线实时预测。

1 物理热模型

物理热模型描述物体热量产生、传递等的一般规律。热力学第二定律是指热量不能自发的从低温物体转移到高温物体，即凡是存在温差的地方，热量自发地从高温物体向低温物体传递，传递过程中的热能常称为热量[23]。利用不同流体及正负极材料，将锂电池内部在充放电过程中产生的热量传递到电池外壁，通过电池箱内部空气的热对流作用带走热量，冷却电池单体，达到散热目的。研究表明，圆柱形电池内部的温度变化随着电池半径的增大而逐渐降低[24]。

为了准确描述电池内部热能传递规律，精确预测锂电池内部电极的实时温度，本文通过安装在电池外侧及电极的温度传感器，根据热量传递的能量守恒定律及经典传热学理论，建立以时间、环境温度、单体电流为输入参数的锂离子电池物理热模型，确定锂电池在实际充放电过程中模型的表面传热系数、导热系数和比热容，以在线实时、准确预测锂电池内部电极处温度，提高运算速度。

1.1 18650型锂离子电池

18650型锂离子电池单体容量小，与层叠式锂离子电池相比，具有开路电压、电芯内阻、使用寿命等重要参数变化小的优点，大量电池串、并联形成电池组时可较好地发挥每节电池的性能，当前新能源电动汽车多采用18650型锂电池为车辆提供动力[25]。18650为电池的外形规格，直径为18 mm，长度为65 mm，0表示圆柱形电池，其他参数如表1所示。

表1 18650型锂离子电池参数

1.2 电池物理热模型

建立18650型圆柱形锂离子电池的笛卡尔坐标系，见图1。

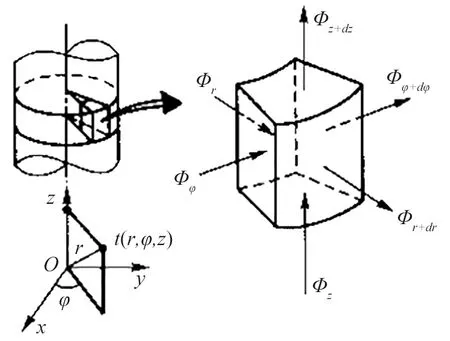
图1 圆柱形锂离子电池的笛卡尔坐标系

1) 圆柱体外侧传热模型

电池外表面与外界环境之间通过对流传递热量。已知圆柱形电池与周围流体间的表面传热系数h及周围流体温度tf，可采用第三类边界条件求解，在笛卡尔坐标系内表示为

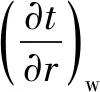
2) 圆柱体中部导热模型

在电池的充放电过程中，锂电池中部产生大量热量，沿径向向外递减。在各个时刻，各点温度组成的集合形成温度分布，又称为温度场。温度场可分为两类：一类是稳态工作条件下的温度场，物体中各点温度不随时间变化，称为稳态温度场或定常温度场；另一类是工作条件变动时的温度场，温度分布随时间改变，称为非稳态温度场，也可称为非定常温度场或瞬态温度场[26]。综合考虑时间、空间对电池内部温度传递规律的影响，本文研究的温度场属于非稳态温度场。

傅里叶导热定律表示在热量传导过程中，单位时间内通过给定界面的热量φ正比于垂直该截面方向上的温度变化率∂t/∂x和截面面积A，而热量传递的方向则与温度升高的方向相反[27]，其数学表达式为

式中：负号表示热量传递的方向，指向热量传递过程中温度降低的方向。

热力学第一定律指出，能量既不能凭空产生，也不能凭空消失，它只能从一种形式转化为另一种形式，或者从一个物体转移到另一个物体，在转移和转化的过程中，能量的总量不变。分析锂电池生热机理，可得热平衡关系：导入微元体的总热量与微元体内热源的生成热之和等于导出微元体的总热量与微元体热力学能的增量之和。

(1)

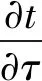
设圆柱体电池半径为r，由式(1)可得圆柱体电池内部瞬态导热微分方程为

(2)

假设电池在径向和轴向上产生的热量比较均匀，由式(1)可知从圆心沿着高度和半径夹角方向温度不变，可等效为零，即可忽略温度沿轴向和角度的扩散，仅考虑温度沿径向的传递，则式(2)中

本文仅考虑电池内部沿垂直于电池外侧半径方向的导热情况，将式(2)中的r等效为n，变换式(2)可得最终的稳态导热微分方程为

(3)

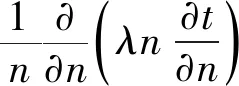
3) 圆柱体电池内部温度计算

由圆柱形电池边界条件的对称性可知

∂t/∂r=0，

(4)

由式(4)可得∂t=0。

式(4)为温度曲线的斜率，即在温度曲线上任取横坐标一点i，对应的纵坐标为j=t(i)，即

t[i,j]-t[(i-1),j]/[i-(i-1)]=0，

可得

t(i)-t(i-1)=0，

(5)

即当前时刻中心温度等于前一时刻相邻的温度，由式(5)可计算圆柱形锂电池内部电极处的温度。

2 在线估算方法分析

2.1 控制方程离散化

离散化是求解连续介质问题的基本手段，它将控制方程划归为有限个参量的代数方程组，可近似代替原方程，常用方法有有限差分法、有限单元法、加权余量法等[28]，有限差分法又分为中心差分法和单侧差分法。若采用单侧差分法，将导致微小热流方向的微小单向传热损失，计算不收敛，温度场畸变，因此选用中心差分法对式(3)进行离散化，离散结果为

式中：Δτ为时间步长，j为时间节点，i为空间节点。

2.2 模型参数辨识

为了模拟车辆行驶时锂电池的充放电过程，对电池采用恒流充放电试验。试验所用仪器有电池充放电测试设备、恒温试验箱、温度传感器和监控电脑等，电池充放电测试仪适用于中小型电池的性能测试，可以完成恒流、恒压、恒功率多个模式的充放电操作；恒温试验箱为试验对象提供所需环境温度，范围为-40～150 ℃，偏差为±2.0 ℃；温度传感器为K型热电偶，测量范围为0～220 ℃，精度为满量程的0.4%。试验过程中确保不过充过放，充放电电流和运行温度不超出允许范围，以免造成电池性能衰减过快，避免发生安全事故。

试验中，将18650型锂离子电池置于恒温试验箱中，在其表面和电极处分别布置温度传感器采集电池表面温度和电极温度。电池表面温度为外部观测温度，是锂电池物理热模型的输入量之一，用电极处采集到的温度近似代替电极温度。

具体试验步骤为：1)设定恒温试验箱温度为所需环境温度25 ℃。2)取1节性能完好(可保证电池完全充放电)的18650型锂电池，将电池静置于25 ℃的恒温试验箱中1 h，保证电池温度与环境温度一致。3)在恒温条件下，以2倍充放电倍率对电池进行放电试验。4)通过热电偶温度传感器监测不同时刻下锂电池放电过程中的表面温度和电极温度，通过监控电脑实时监测并记录电池电极温度和表面温度随时间变化的数据，如图2所示。

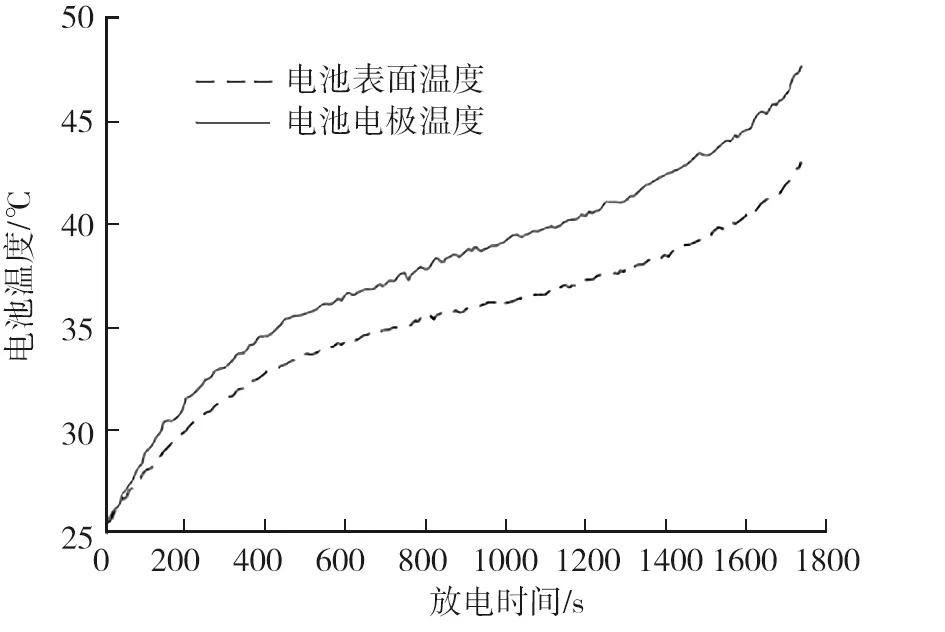
图2 2倍充率下电池表面温度和电极温度

由图2可知：在放电初期，电池电极温度较低，电解液中导电锂离子活性较差，电池内阻分压较大，该阶段电池内部产生的热量急速增加，电池温度急剧上升；随着放电过程的进行，电池内部温度持续上升，内部导电离子活性增加，内阻逐渐减小，电池温度上升趋于平缓；当放电即将结束时，电池内部内阻急剧增大，电池放电电压迅速降至放电截止电压，导致该阶段电池内部产生的热量急速升高，电池温度急剧上升。

由电池物理热模型(圆柱体外侧传热模型和中部导热模型)可知，只需确定模型的c、λ和h，即可计算电池内部温度。c反映电池内部温度的升温速度，c越大升温越慢；λ反映电池内部的温度分布情况，λ越大，温度分布越均匀；h是电池外侧和外界空气间的换热系数，决定圆柱体电池外侧温度。采用MATLAB软件计算、标定电池各项导热参数，锂电池c=1.63 kJ/(kg·K)，λ=27.61 W/(m·K)，h=34.32 W/(m2·K)。

2.3 电池内部电极温度在线预测结果与分析

为验证所建模型预测的锂电池内部的电极温度的准确性，在MATLAB中将传感器采集到的电池表面温度、环境温度及电流等数据代入式(3)，计算电池内部电极温度，并与温度传感器采集的电极温度对比，其预测结果及预测误差E如图3所示。

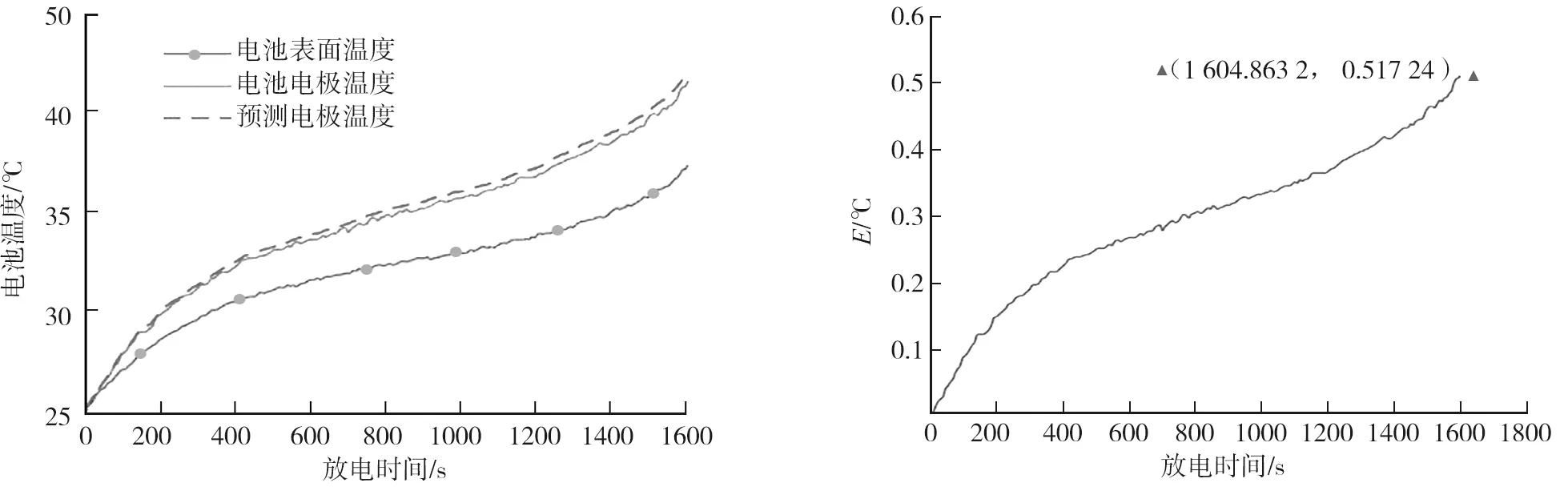
a)预测电池温度 b)预测温度误差图3 电池温度与放电时间关系曲线

由图3a)可以看出：模型预测结果与试验结果较吻合，预测准确性依赖于锂电池c、λ和h的辨识结果。由图3b)可见：电极温度的预测结果与温度传感器测量结果非常接近，最大误差为0.517 4 ℃，平均误差为0.002 ℃，接近0，计算模型预测结果仅用时1.5 ms，完全可以在线实时监测锂离子的电极温度。

3 结语

基于经典传热学理论及热量传递的能量守恒定律，建立锂离子电池内部电极温度预测模型，在25 ℃常温状态下，采用2C放电倍率对其进行标定并验证。试验结果显示：此物理热模型可精确预测锂离子电池内部的电极温度，实时反映锂电池内部温度的变化情况，为研究纯电动汽车电池热管理系统提供可靠依据。