两个保序全变换半群的直积上的自同构
2021-06-17 05:56尚传翠杨秀良
杭州师范大学学报(自然科学版) 2021年3期
尚传翠,杨秀良
(杭州师范大学理学院,浙江 杭州 311121)
1 引言和主要结果叙述

本文的主要结果如下:
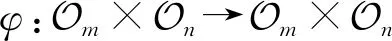
其中


2 主要结果的证明
为叙述方便,先做如下准备:
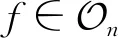
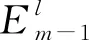

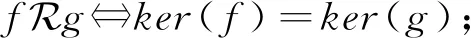



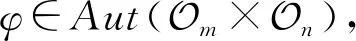
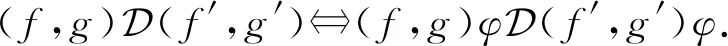

进而
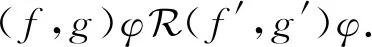
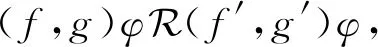
进而
又因为φ是单射,故

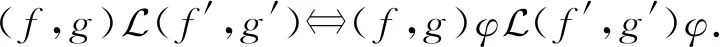
进而


进而
又因为φ是单射,故

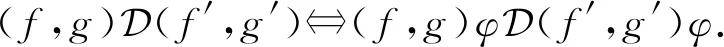
□
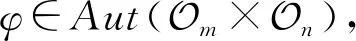
证明由引理1知

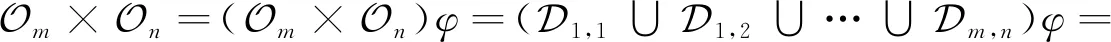
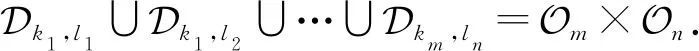
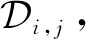

由m,n的任意性得
进而

□

证明任取(z1,z2)∈Xm×Xn,则

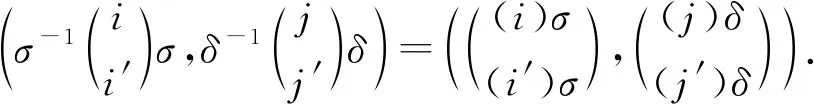
□
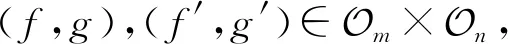
[(f,g)(f′,g′)]φ=(ff′,gg′)φ=(σ-1ff′σ,δ-1gg′δ)=
(σ-1fσσ-1f′σ,δ-1g′δδ-1g′δ)=
(σ-1fσ,δ-1gδ)(σ-1f′σ,δ-1g′δ)=
(f,g)φ(f′,g′)φ.

任取(f,g)φ=(f′,g′)φ,则
(σ-1fσ,δ-1gδ)=(σ-1f′σ,δ-1g′δ),
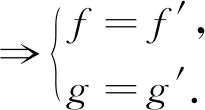
⟹(f,g)=(f′,g′).

特别地,
故
不妨设x′=σ(x),y′=δ(y).因为φ是双射,则σ∈Sm,δ∈Sn.进而
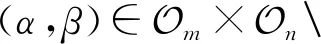


令(x)σ=s,(y)δ=t,s∈Xm,t∈Xn,则x=(s)σ-1,y=(t)δ-1.进而
⟹(α,β)φ=(σ-1ασ,δ-1βδ).
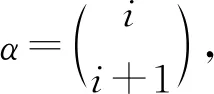
假设存在i∈Xm,使得(i)σ<(i+2)σ<(i+1)σ,则
假设存在i∈Xm,使得(i)σ>(i+2)σ>(i+1)σ,则
故任取i∈Xm,有

即

同理可得




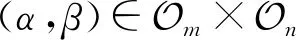


□
猜你喜欢
玻璃纤维(2022年1期)2022-03-11
南方医科大学学报(2021年10期)2021-11-10
新世纪智能(数学备考)(2021年11期)2021-03-08
新世纪智能(数学备考)(2020年11期)2021-01-04
杭州(2020年6期)2020-05-03
中等数学(2019年4期)2019-08-30
电影(2017年1期)2017-06-15
汽车与安全(2016年5期)2016-12-01
看天下(2016年24期)2016-09-10
少儿科学周刊·少年版(2015年1期)2015-07-07

