基于股票分析与灰关联的JTC轨面设备故障诊断方法

崔一博，赵林海，吕向东

(1.北京交通大学 电子信息工程学院, 北京 100044；2.中国铁路郑州局集团有限公司 电务部，河南 郑州 450000)

补偿电容和调谐单元作为无绝缘轨道电路(Jointless Track Circuit, JTC)的轨面设备，主要用于保障信号的传输质量[1]和防止邻区段信号的越区传输[2]。由现场调研可知，JTC轨面设备的故障模式主要表现为补偿电容断线、容值下降和调谐单元断线等[3-4]。这些故障易造成JTC“红光带”和轨道电路读取器(Track Circuit Reader, TCR)“掉码”等问题[5]。

目前，铁路现场主要采用电务检测车定期巡检[6-7]的方式来检测这些故障，但这并不能及时发现检测间隔期间具有突发性的补偿电容和调谐单元断线故障。对此，人们尝试利用TCR的记录数据及其远程监测平台，将TCR作为检测设备，以提高轨面设备的检测效率。

目前，对于轨面设备的故障诊断，普遍是分别针对补偿电容[8-17]和调谐单元[2,18]开展研究。文献[19]是从轨面设备整体的角度，尝试利用模糊定性趋势分析的方法实现对补偿电容和调谐单元的故障诊断。然而该方法没有考虑多个补偿电容同时故障以及调谐单元与补偿电容组合故障等情况。故本文针对这一情况，将TCR感应电压幅值包络的变化与股票价格的波动相联系，利用完善的股票分析技术提取故障特征，再利用灰关联技术实现故障模式匹配，最终实现轨面设备间组合故障的诊断。

1 轨面设备对TCR感应电压幅值包络的影响分析

JTC和TCR的基本结构和工作原理见图1。图1中，JTC信号由发送器产生，经发送电缆和匹配变压器传送至调谐区，并沿钢轨向接收器传送。调谐区包含有BA1和BA2两个调谐单元和一个空芯线圈SVA。当轨道被列车占用后，JTC信号的绝大部分经列车第一轮对分路后回流，TCR设备利用接收线圈，通过电磁感应的方式接收JTC信号生成相应感应电压信号，而后该感应电压信号经TCR传输电缆传送至TCR主机。

图1 JTC和TCR的基本结构和工作原理

对于本文来说，需要考虑的故障设备主要是轨面上的所有补偿电容和发送端调谐区的两个调谐单元BA1和BA2。因此，其故障模式主要有：单个和多个补偿电容故障，单个和多个调谐单元BA1和BA2故障，以及补偿电容和调谐单元组合故障。在此，利用文献[2，19-20]建立感应电压幅值包络模型，设置仿真条件为：轨道电路长度988 m；信号载频2 600 Hz；道砟电阻1 Ω·km；发送端输入电平135 V；分路电阻0.15 Ω；补偿电容容值40 μF；电容个数10。分别对轨面设备正常，C8断线，C8与C6断线，BA1故障，BA2故障，BA1与BA2故障，BA1与C8故障，BA2与C8故障，BA1、BA2与C8故障等9种情况进行仿真。其中，补偿电容C1～C10依次指JTC从接收端到发送端第1至第10个电容；BA1与BA2与图1相同，发送端靠近主轨的调谐单元为BA1，另一个调谐单元为BA2。

根据文献[2]信号归一化公式，记机车第一轮对所在钢轨分路点x处的感应电压归一化幅值为Acv(x)，则Acv(x)的仿真结果见图2。

图2 JTC正常与轨面设备不同故障模式下的Acv(x)仿真结果

正常情况：补偿电容使得感应电压幅值包络从JTC发送端到接收端呈“波浪式”衰减，在每个电容位置取得局部极小值。

补偿电容单独故障：C8单独故障只影响到C1～C8间的信号幅值，且C6到C7之间的幅值单调下降，而C7到C8之间的幅值单调上升。

多个补偿电容组合故障：C6和C8同时断线时，受两个电容故障的影响，信号在C5与C7位置形成两个局部极小值。

调谐单元BA1故障：对发送端两个电容C9、C10处信号幅值影响最大，两个电容之间的信号幅值出现新的单调性，发送端到C10间信号幅值下降速度增大。

调谐单元BA2故障：使得发送端调谐区至C10间信号幅值的单调性被破坏，呈现出近似抛物线的变化。

调谐单元与电容同时故障：调谐单元故障主要对接近调谐区的3～4个补偿电容范围信号幅值产生影响，C8断线则影响接收端到C8间的信号幅值。

综上可知，补偿电容和调谐单元的故障均会对TCR感应电压幅值包络产生影响，且不同的故障模式对其的影响规律不尽相同。

2 JTC轨面设备故障诊断算法设计

2.1 设计思路

众所周知，股票价格会受多种因素的影响而随时间的变化表现出不同形式的变动。某股票一段时期内的价格曲线[21]见图3。从图3可以看出，该股票价格在按一定频率进行上下波动的同时，还存在一个总体的上升趋势，而这一变化规律与图2中部分TCR感应电压幅值包络的变化非常类似。这表明，仅就数据而言，股票价格与本文的TCR感应电压幅值包络数据本质上同属于幅值变动的时间序列，而本文数据应属股票价格数据众多变化中的一类。显然，能够胜任股票分析的各特征指标，原则上也应能够用于本文数据故障特征的构建。

图3 某股票价格曲线

由此，本文借鉴股票分析技术，将TCR感应电压幅值包络曲线映射为相应的股票价格，再基于股票完善的分析指标构造出相应的故障特征，最终利用灰关联分辨系数实现对轨面设备的故障诊断。基于股票分析和灰关联的JTC轨面设备故障诊断总流程见图4。

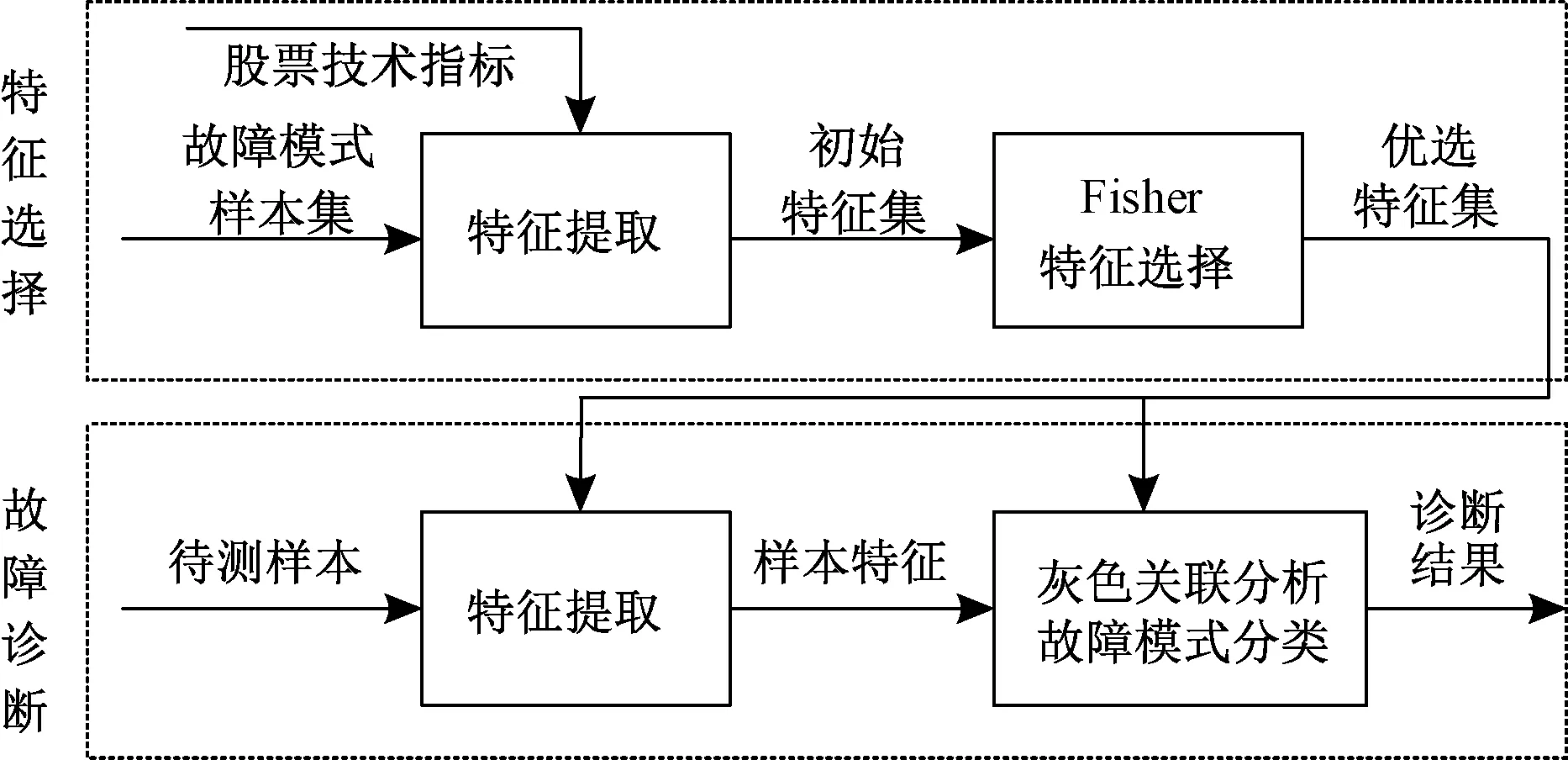
图4 轨面设备故障诊断总流程

由图4可知，本文的故障诊断过程主要分为特征选择和故障诊断两部分。在特征选择部分，首先构建包含所研究的所有故障模式的模式样本集；再利用常用股票技术指标对每个样本进行特征提取，并通过Fisher分值法进行特征选择；最终构建最优模式特征集。在故障诊断部分，首先利用已选特征对待测信号进行特征提取；然后再利用待测信号故障特征与模式样本特征集中各故障模式特征的灰关联度，实现轨面设备的故障诊断。

2.2 基于股票技术指标的故障特征提取

常用的股票技术指标有威廉离散变异量(William’s Variable Accumulation Distribution, WVAD)、相对强弱指数(Relative Strength Index, RSI)、幅度涨速(Amplitude Increase Rate, ACCER)、价格动量(Capacity Rate, CR)、移动平均线(Moving Average, MA)、布林线(Bollinger Bands, BOLL)、K线积分和异同平均线(Moving Average Convergence/Divergence, MACD)等。在此，设ps(t) (t=1,2,…,Ts)为在一天中1～Ts时间内股票的价格变化，pl(t)为在第t(t=1,2,…,Tl)日的股票价格情况，则以上各股票技术指标的计算公式及其含义[21]见表1。

表1 常用股票技术指标的计算公式及其含义

基于表1所列各股票指标对感应电压幅值包络进行特征提取。设一个JTC长度为lg，其所含补偿电容总数为m，以各补偿电容所在位置为分界点将Acv(x)分为m+1段，则有

(1)

在此，将各Acv(k)(x)分别映射为表1中相应的ps(t) 和pl(t) ，以计算以上J(J=10)个股票技术指标。

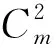
(2)

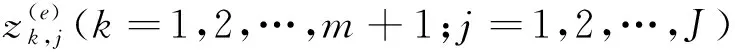
(3)

对于所有E个样本，其对应的特征集为

(4)

2.3 基于Fisher准则的故障特征选择

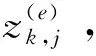
(5)

设特征集内的第k段数据第j个特征的类间方差与类内方差分别为αk,j、βk,j，则该特征的Fisher分值sk,j为

(6)

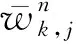
(7)

由式(6)～式(7)计算得到Fisher矩阵S为

(8)

分别对S中的每一行按从大到小顺序排列，则第k行为

[sk,j(1),sk,j(2),…，sk,j(J)]

sk,j(1)>sk,j(2)>…>sk,j(J)

(9)

从中选择j(1)到j(g)的前g(1≤g≤J)个较大的Fisher分值所对应的股票技术指标，作为第k段数据所选择的特征指标，即

[zk,j(1),zk,j(2),…,zk,j(g)] 1≤g≤J

(10)

对式(8)中S的各行，分别执行式(9)～式(10)以得到选择好的特征指标，将每行的特征指标按顺序排成一行以构建感应电压幅值包络最终选择的特征向量，设为Zcv，经归一化处理后得

(11)

2.4 基于灰关联分析方法的故障模式分类

设模式特征集为Zlv，其中包含m个补偿电容，载频为1 700、2 000、2 300、2 600 Hz时式(2)中的N种JTC模式，即

(12)

(13)

p=1,2,…,g×(m+1)

(14)

(15)

设待测样本的JTC频段为第fc种，同一故障模式包含4种频率下的灰关联度，故障模式最终灰关联度为

Rn=Rn,fc

(16)

基于以上分析，利用灰关联分析对JTC轨面设备进行故障诊断，其诊断流程见图5。

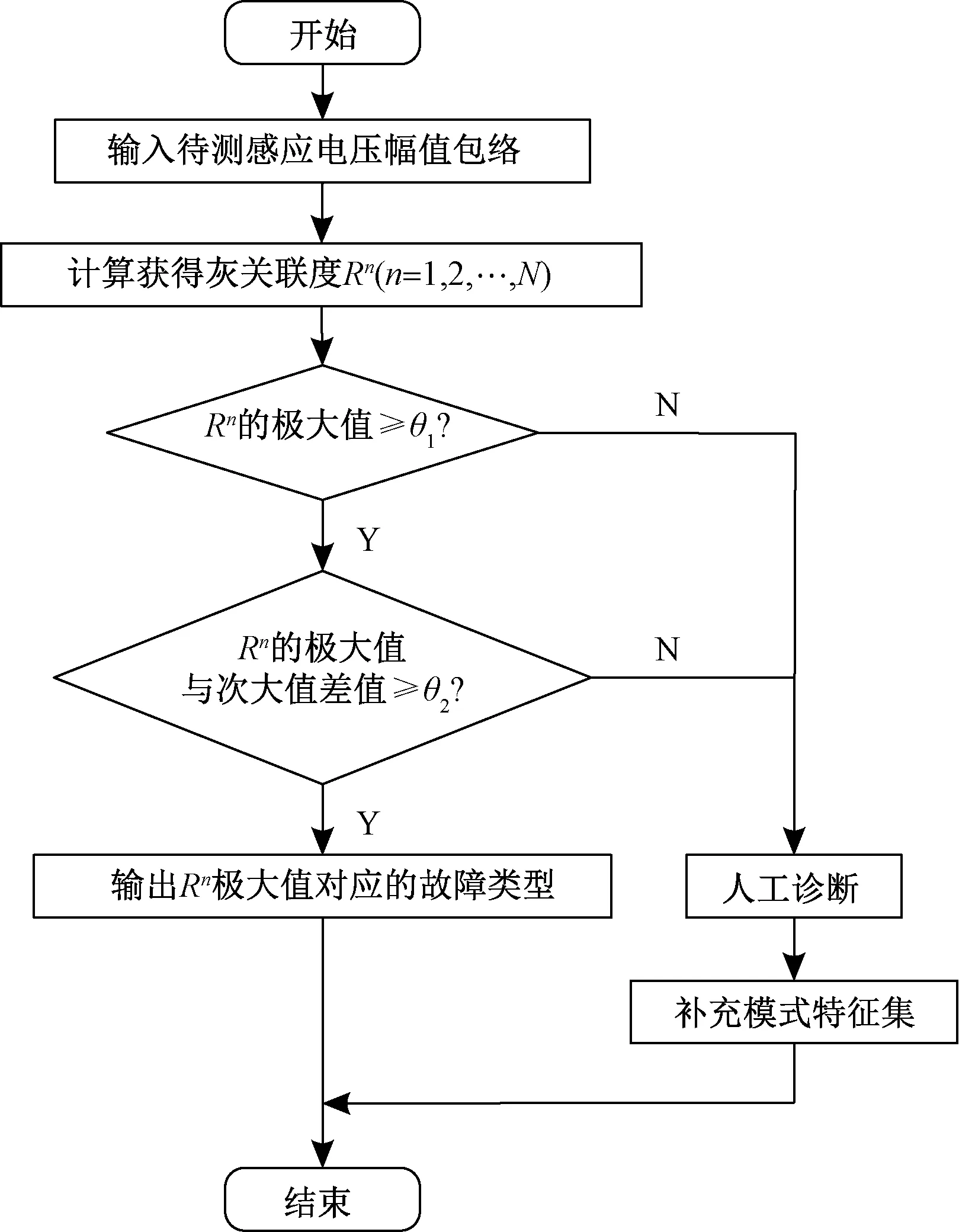
图5 故障诊断流程

对计算获得的待测样本与各故障类型的灰关联度Rn(n=1,2,…,N)进行分析，当Rn的极大值大于诊断阈值θ1且极大值与次大值的差值大于阈值θ2时，则判断灰关联度极大值所对应的故障类型为待测样本的故障类型，反之则认为算法无法识别当前样本的故障情况，进行人工诊断。在人工识别后将该样本补充到模式样本集内，使得之后算法对相同类别的故障可以识别。θ1和θ2的设置可根据实际要求决定。θ1越大，要求待检样本与模式样本的故障模式的相关度越大。θ2主要用于区分待测样本同时与两个故障类型相关度较高时待测样本的具体故障情况。

3 实验验证

3.1 评价指标的确定

在此，用拒识率μd、虚警率μo、漏报率μr、误报率μm和准确率μq作为算法性能评价的标准。

(17)

式中：ys为被诊断的JTC区段个数；yz为JTC轨面设备正常而本文算法判定存在故障的区段个数；yl为JTC轨面设备故障而本文算法判定为正常的区段个数；yu为JTC轨面设备故障而本文算法对故障设备诊断错误的区段个数；yc为算法提示进行人工诊断的区段个数。

3.2 故障模式特征样本集主要参数的确定

为了验证算法的有效性，取不同频率、不同道砟电阻、不同长度、补偿电容个数为m=16的JTC感应电压幅值包络数据进行仿真，由式(2)可知其故障情况共188种。每种模式选取10个数据样本，按2.2节与2.3节进行特征提取和选择，再按2.4节进行故障模式分类实验。

3.2.1 股票特征个数g

由2.3节可知，对感应电压幅值包络分段计算各个指标的Fisher分值，将其从大到小排列后，选择排名前g个高分值指标作为故障特征。故g的取值直接关系到故障特征集的大小和故障诊断性能。在此，分别令g=1,2,…,10，重复图5的故障诊断流程对所有数据进行故障诊断，并按式(17)计算g取不同值时的准确率。g不同取值下的算法准确率见图6。

图6 g不同取值下的算法准确率

由图6可知，准确率随着g取值的增大而增大，并在g=5时达到最大。之后，准确率随着g取值的增大而减小。故本文取g=5。

3.2.2 道砟电阻

在基于式(4)构建故障模式样本集的过程中，道砟电阻如何取值才能使诊断结果的准确率最高，是一个需要研究的问题。为此，本文令道砟电阻Rd分别取1、2、…、10 Ω·km，并以此构建相应的故障模式样本集，再计算出对应的算法准确率。不同道砟电阻所对应模式特征集下的算法准确率见图7。

图7 不同道砟电阻所对应模式特征集下的算法准确率

由图7可知，当道砟电阻取其临界最小值1 Ω·km时所构建的故障模式样本集并非最优，其对应的诊断正确率仅约为60%。随着道砟电阻的增大，相应构建特征集所对应的准确率也逐步提高，并在3 Ω·km之后趋于稳定，而在Rd=5 Ω·km时达到最大，故本文将模式样本集的道砟电阻设为5 Ω·km。

3.3 灰关联分辨系数ξ的确定

式(14)中灰关联度分辨系数ξ的主要作用是使待测样本与当前模式样本的灰色关联度，不仅受到本身的影响，还与整个模式样本有关，其大小也决定着关联度模型对异常值的敏感程度。因此，需要确定分辨系数ξ的最优取值。基于仿真数据集，分别计算分辨系数由0.01到1，步长为0.01变化时的识别率。ξ不同取值下的算法准确率见图8。

图8 分辨系数不同取值下的算法准确率

由图8可知，随着分辨系数ξ增大，算法准确率单调上升，当ξ≥0.47时，算法准确率趋于稳定。因此，本文取ξ=0.5。

3.4 基于文献[19]的实验

基于文献[19]的测试条件，对本文算法进行实验，其实验结果见表2。

表2 文献[19]仿真条件下的本文算法准确率 %

由表2并结合文献[19]的数据可以得出，本文算法在各信噪比下的平均准确率均高于文献[19]，且本文算法对道砟电阻不敏感，在道砟电阻大于1 Ω·km时，其算法准确率几乎不受道砟电阻的影响。

3.5 现场数据验证

3.5.1 算法正确性验证

某局管内JTC区段TCR感应电压幅值包络实际数据见图9，该区段补偿电容数为16。经电务检测车检测，该区段补偿电容C1、C15断线，其余轨面设备正常。

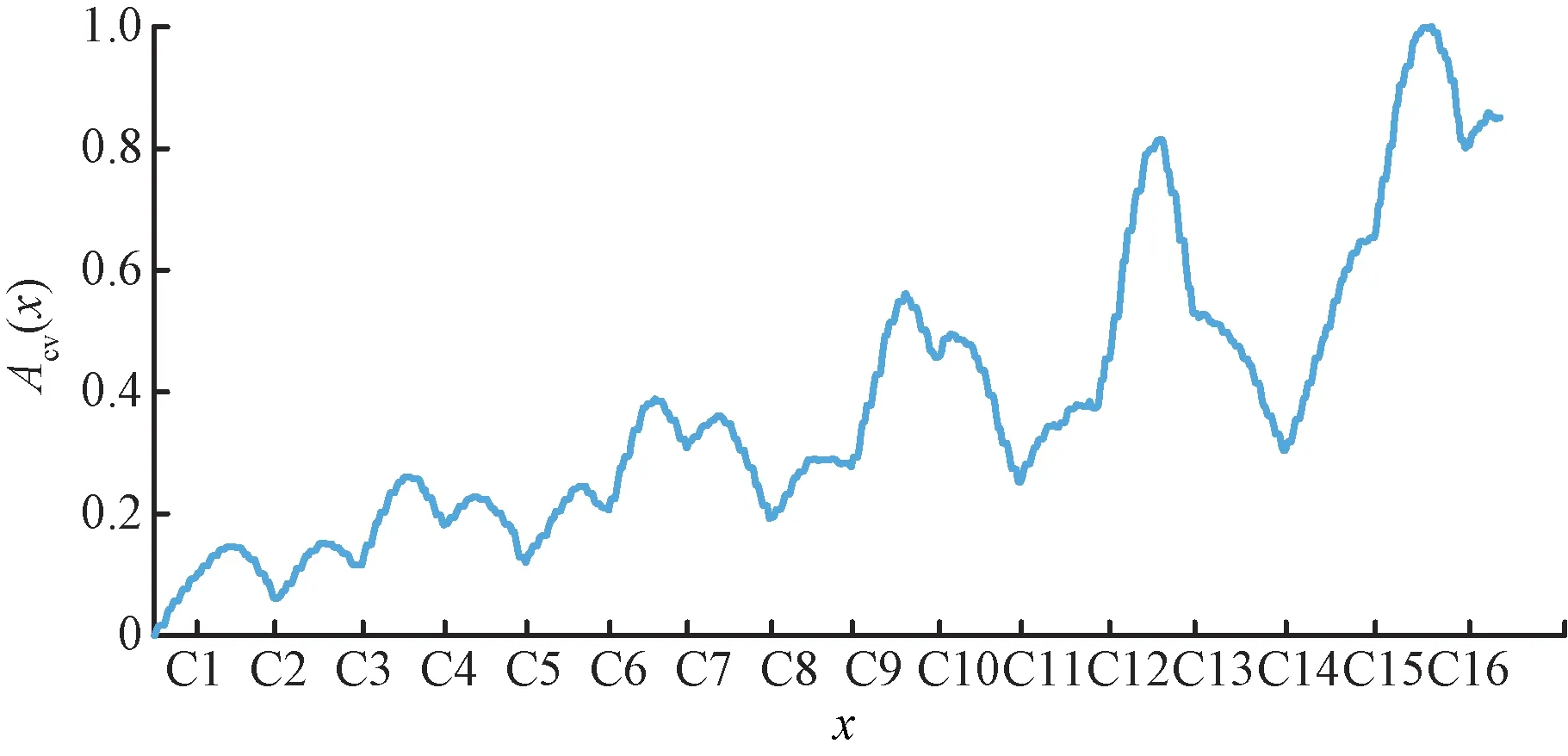
图9 某局管内一JTC区段所对应的Acv(x)实际数据

在利用股票技术指标计算特征后，令g=5。模式样本集道砟电阻Rd=5 Ω·km，分辨系数ξ=0.5。对待测样本进行特征提取后，计算待测样本与各故障模式的灰关联度，其计算结果见图10。

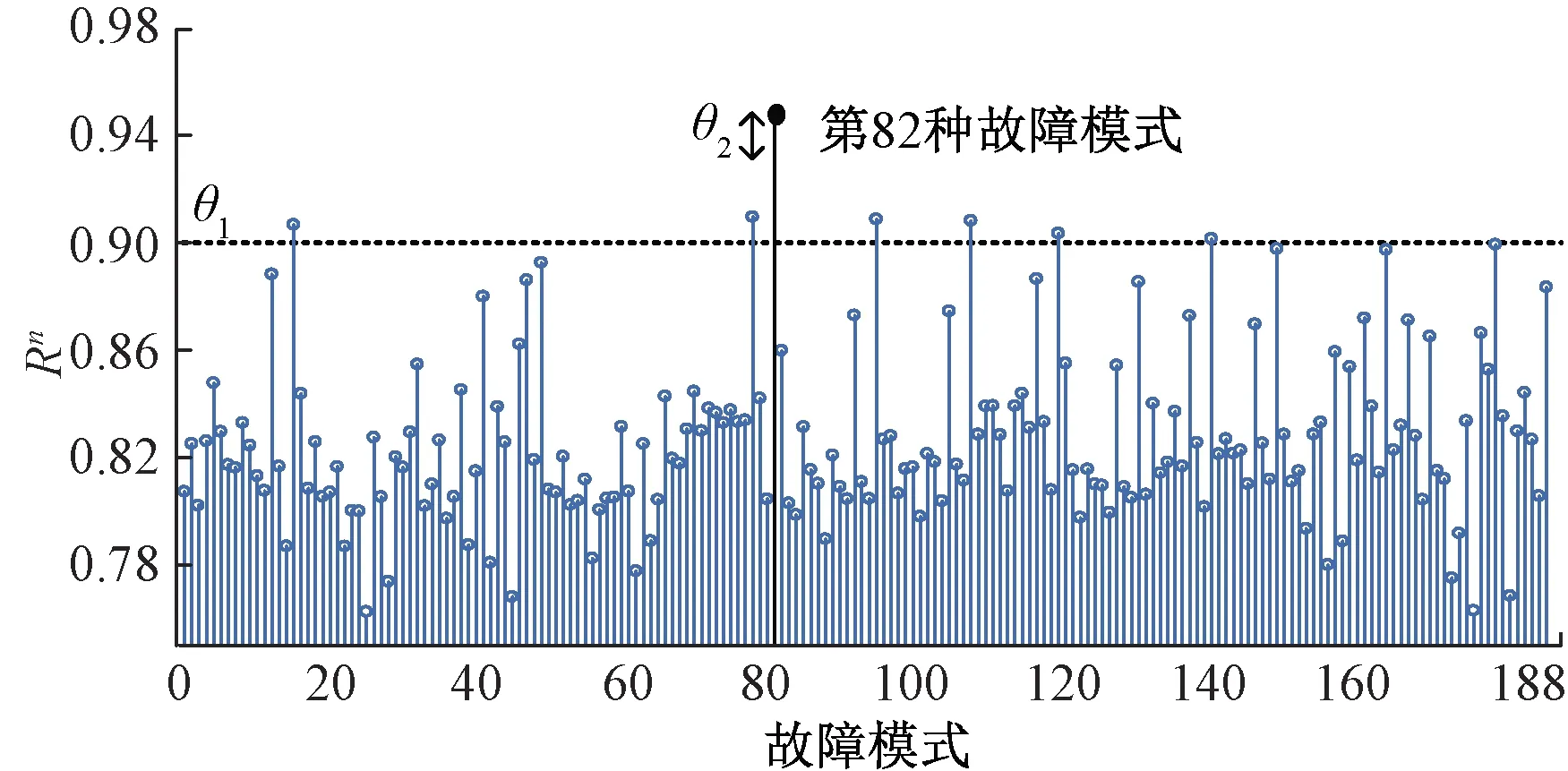
图10 待测样本与模式样本集的灰关联度

基于图5的故障识别策略，并结合诊断阈值θ1=0.9和θ2=0.02的设定值，第82种故障类型具有最大灰关联度，第17种故障类型具有次大灰关联度。图10中最大灰关联度大于θ1，最大灰关联度与次大灰关联度差值大于θ2，以此判断故障模式为第82种。在故障模式定义中属于补偿电容C1、C15断线，这与现场实际检测结果一致，证明了本文算法对轨面设备故障诊断的有效性。

3.5.2 算法性能分析

选取某线路三年内同一条运行交路的500个JTC区段所对应的感应电压实际数据作为算法性能测试集。其中，所选数据在其生成时间和所对应的JTC的地理分布、长度、信号载频和补偿电容个数等方面力求全面，以检验不同季节、不同外部环境和JTC不同配置对本文算法性能的影响。算法性能测试集的诊断结果见表3。

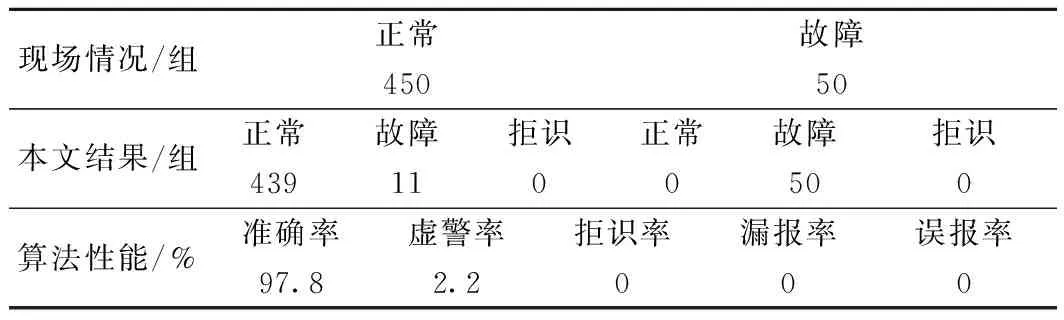
表3 算法性能测试结果

由表3可知，本文算法的准确率为97.8%，虚警率为2.2%，没有拒识、漏报和误报。这表明本文基于股票分析指标所构建的故障特征是有效的，其完全能够满足本文进行故障诊断的要求。

本文的虚警情况主要集中于发送端第一个补偿电容上，由于第一个补偿电容与发送端调谐区之间只有半个补偿间距，受信号采集和调谐区的影响，部分数据在这两个电容位置处的波动规律没有得到充分体现，从而出现虚警的现象。

需要强调的是，由于算法性能测试集中的数据来自三年内不同地点和时间节点，受天气、温度、季节的影响使得各数据的道砟电阻不尽相同。故由测试结果可知，本文算法受道砟电阻影响较小。

此外，在实时性上，本文基于Windows10操作系统，在CPU型号为i5-4200，系统内存为8 GB的条件下，对上述500组数据进行连续故障诊断，总用时约为2.64 s，平均单组数据执行时间约为0.005 s。可见，由于本文算法不涉及复杂的网络学习过程，故其具有较好的实时性。

4 结论

在列控系统中，JTC主要负责列车占用检查和地-车间信息传输，而调谐单元和补偿电容作为JTC的轨面设备，其故障会对JTC和TCR造成影响。对此，本文基于TCR感应电压幅值包络与股票价格波动的相似性，根据补偿电容的位置对感应电压幅值包络进行分段，再对分段数据利用股票技术指标提取故障特征，并基于各特征的Fisher分值构建各故障模型的最优特征集。最后通过计算待测样本与最优特征集中不同故障模式特征的灰关联度，实现待测样本的故障模式匹配。此外，本文还进一步分析单段数据选取股票特征个数g和分辨系数ξ最优值的确定，以及道砟电阻对故障特征集的影响。实验表明，该方法具有准确率高和适应性好等特点。经现场实际数据检验，各类故障的诊断准确率达到97.8%，虚警率为2.2%，且无拒识、漏报和误报，能够满足铁路现场的实际需求。