基于C-LSTM的传感器数据流半监督在线异常检测算法∗
唐海贤李光辉∗
(1.江南大学人工智能与计算机学院,江苏 无锡214122;2.物联网技术应用教育部工程技术研究中心,江苏 无锡214122)
传感器网络经常被于环境监测领域,传感器节点需要不间断地采集环境参数,形成随时间变化的传感器数据流。受监测环境、通信信道或节点本身等多方面因素的影响,传感器节点采集到的原始数据流会不可避免地存在缺失、数据异常等问题。传感器数据流的异常检测是为了及时发现数据流中与正常模式有明显差异的数据[1]。检测到异常数据之后,便可以实现对环境事件的实时报警、异常数据修复、节点故障修复等应用。因此,传感器数据流的异常检测对于监测系统的可靠性保障和管理部门的决策支持均有重要意义[2]。
数据流的异常检测是数据科学中非常重要的一方面。近年来,已经有大量的研究者利用机器学习方法,提取数据流(比如传感器数据流)的特征来进行数据流的异常检测[3]。根据异常检测的建模类型,数据流的异常检测方法分为三类[4]:统计建模方法、时序特征建模方法、空间特征建模方法。异常检测算法按照是否需要人工标注好的数据集,则可将数据异常检测算法分为有监督学习异常检测算法和无监督学习异常检测算法。
Wazid等人[5]利用K-means聚类算法检测无线传感网络(WSN)的入侵异常。他们通过分析数据流的统计特征,计算出正常数据和异常数据的聚类中心。并通过计算WSN数据与聚类中心的欧氏距离进行异常检测,对特定种类的入侵异常有较高的检测准确率。Lee等人[6]将SOM算法[7]与K-means聚类结合,实现了在线异常检测。该算法通过实时更新的网络结构,并利用新数据的适应程度重建异常簇或拆分正常簇,实现了对新型异常的检测。这类算法在检测统计异常时具有高的检测准确率,并且不需要提前标注数据集,是无监督异常检测算法,但是它们难以区分与异常数据具有相似分布的正常数据。
Wu等人[8]研究了LSTM算法[9]在工业物联网传感器数据流异常检测中的应用。他们使用LSTM模型预测未来数据,通过预测值与实际值的误差检测异常数据。Feng等人[10]利用LSTM模型提取工业控制系统数据的时序特征,并使用Softmax分类异常数据。这些方法利用RNN提取数据流的时序特征,通过预测算法预测未来数据,并利用预测值与真实值的误差检测异常值;或者使用分类算法检测异常数据。这类算法对于具有确定时序特征的数据流有好的检测准确率,对于不具有确定时序特征的数据流无法准确检测。
Shi等人[11]研究了将CNN与LSTM结合来预测未来的降水强度。他们利用CNN和LSTM提取数据的时间与空间特征[12],使用预测算法预测未来数据。Kim等人[13]使用C-LSTM模型检测网络流量数据的异常值。该算法利用CNN提取数据的空间特征,利用LSTM提取数据的时间特征,并利用预测算法或分类算法检测异常数据。该算法对具有明显时空特征的数据具有好的检测准确率。但是这类有监督学习异常检测算法对于数据集的构建有很高要求,需要训练集尽可能包含全部的异常种类,并有足够的数据量。但是现实中,环境监测数据流具有正常数据和异常数据占比不平衡、数据随时间会有较明显的周期性波动、异常数据种类多样等特点[4],很难对采集的数据进行准确的标注,或者很难获取纯净的数据(全部是正常值的数据),因此不能有效检测新型异常。
综上所述,不需要提前标注数据的无监督异常检测算法有很大的局限性,只适合检测统计异常。有监督异常检测算法可以有效利用环境监测数据流的时空特性,对各种异常都有高的检测准确率,但是难以获取有效的有标注数据集。因此,需要针对环境监测数据流研究既能有效检测具有时空特征的异常数据,又能有效检测新型异常数据的半监督异常检测算法[6,14]。为实现上述目标,本文针对到达服务器端的环境监测传感器数据流,提出了一种基于C-LSTM的传感器数据流半监督在线异常检测算法(Semi-Supervised Online Anomaly Detection Algorithm of Sensor Data Stream Using C-LSTM Neural Network,简记为C-LKM)。
1 C-LSTM模型和K-means算法简介
1.1 C-LSTM模型
C-LSTM模型是一种将卷积神经网络(CNN)与长短时记忆网络(LSTM)相结合,来分类时序序列的多层前馈网络[13],网络结构如图1所示。C-LSTM网络利用时序序列作为输入,经卷积神经网络提取高维特征,并将卷积神经网络最后一层最大池化层(Max Pooling)的输出作为LSTM网络的输入。将LSTM网络提取的特征展开,经过全连接层进一步提取输入数据的特征,最终利用Softmax函数,获取输入数据的预测结果。
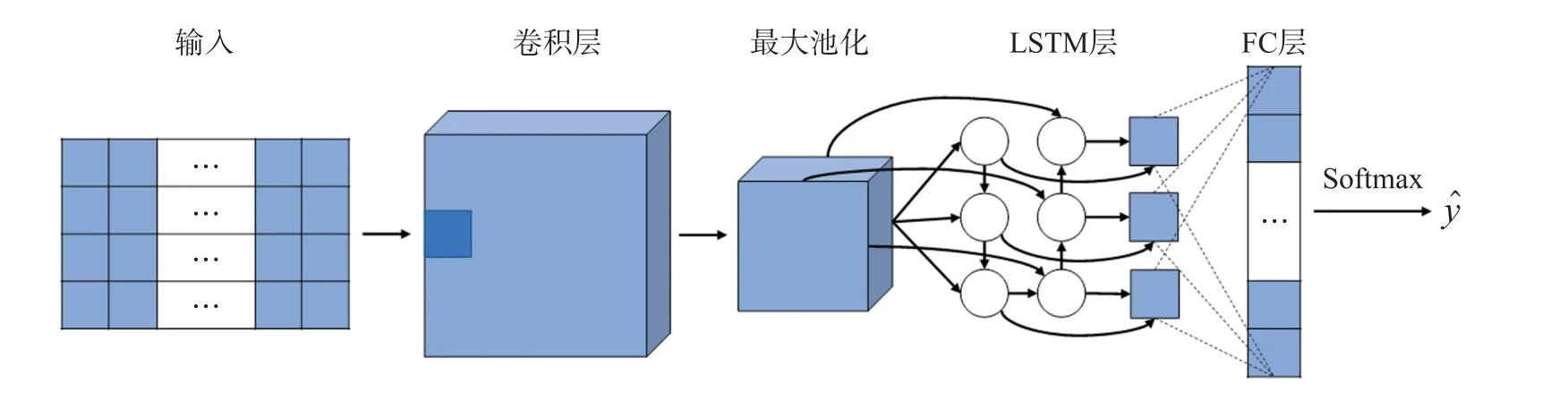
图1 C-LSTM网络模型
其中LSTM网络采用加入peephole connection的LSTM模型[15],其特点是在三个控制门的输入分别加入细胞状态信息。其状态方程为:
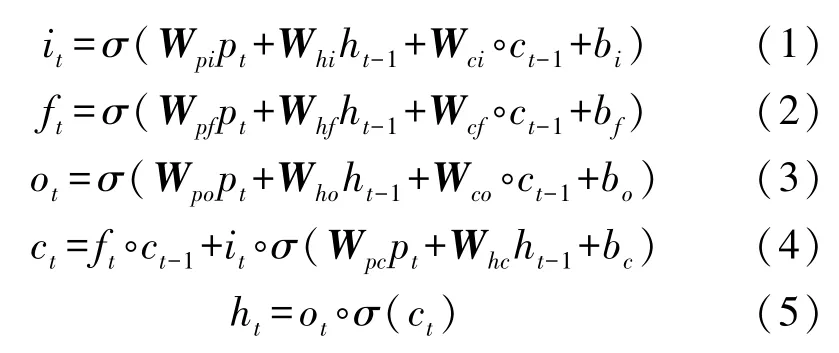
式(1)~式(5)使用的符号:i,f,o分别代表着LSTM的输入、遗忘门、以及输出门。式(1)~式(5)使用的符号c、h分别代表着LSTM网络一个单元的状态,以及隐藏层的状态。σ为激活函数,比如tanh、Relu函数。W代表LSTM对应门的权值矩阵,b为偏置。Pt用于表示LSTM网络t时刻的输入,其输入为CNN网络的池化层在t时刻的输出。其中符号°表示矩阵Hadamard乘积。LSTM单元为模型提取了传感器数据流在时间上的特征。
使用Softmax函数对LSTM网络的输出进行判别,判断结果为0或1。0代表正常数据,1代表异常数据。
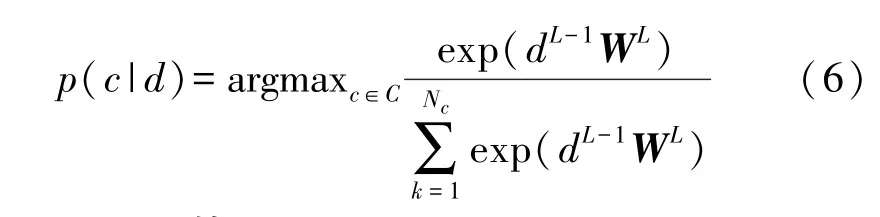
1.2 K-means算法
K-means即K均值算法,是一种无监督的聚类算法[16]。对于给定样本D,K-means算法针对聚类所得簇C={c1,c2,c3,c4}最小化平方误差。这里使用欧氏距离作为两点之间的距离,进行聚类。
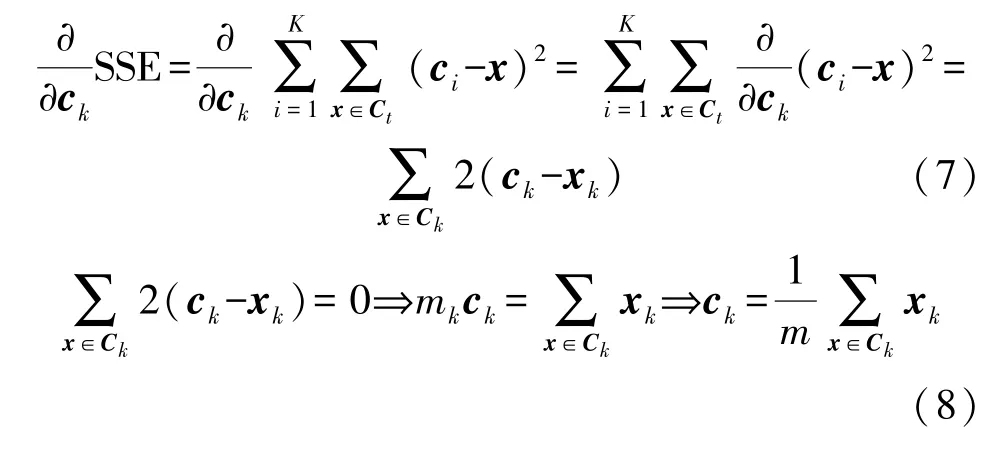
2 基于C-LSTM的传感器数据流半监督在线异常检测算法(C-LKM)
2.1 C-LSTM模型结构
C-LSTM模型使用了CNN和LSTM两种神经网络,LSTM利用CNN提取的传感器数据流高维特征作为输入,并继续提取其时间特征,最后经全连接层压缩数据后,交由Softmax函数判定是否为异常。CLSTM网络的预测结果为Yclstm。
C-LSTM模型可以根据实际应用调整其网络结构,令其包含不同数量的卷积层、池化层、LSTM隐藏层。同时,变量数量也会发生变化。模型的大小以及变量数量会影响最终的识别效果以及识别速度。一般来说,模型规模越大,识别效果越好,识别速度越慢。同时,C-LSTM模型可以适应不同尺度的输入数据,在改变输入数据的尺寸(维数、窗口长度)时,模型需要微调。
本文的输入是时间窗口长度l=101的传感器数据流,每条数据包含4个属性,使用两层卷积加上两层LSTM的C-LSTM网络结构来检测输入数据的异常信息,每层LSTM网络包含64个节点。其网络结构如表1所示。该网络结构包含两个卷积层,两个池化层,一个LSTM网络,两个全连接层,用tanh函数作为激活函数。在卷积层,使用的卷积核大小为5,卷积步长为1,对输入数据均不使用padding。在池化层,使用最大池化来压缩特征数量,池化核尺寸为2,池化步长为2。使用卷积层最后一层池化层的输出作为LSTM网络的输入。使用tanh函数作为C-LSTM网络的激活函数。
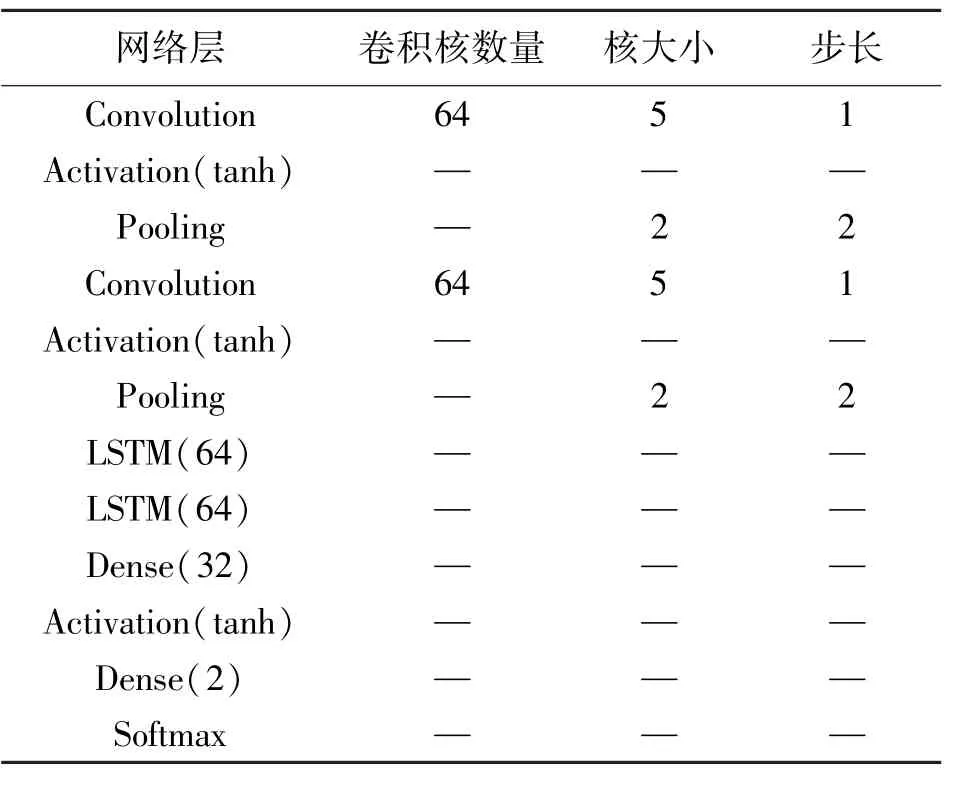
表1 C-LSTM网络结构
tanh函数用于将一个实数映射到[-1,1]范围内,当输入为0时,tanh函数的输出也为0。Tanh函数对中间部分的变化敏感,并可以有效抑制两端,对分类有利[17]。本文使用tanh函数作为激活函数,一方面可以在传感器数据流出现异常后,有效地捕捉到传感器数据流的细微变化,另一方面能够将网络输出数据压缩到[-1,1]之间,使得数据在卷积神经网络的层与层之间传递时不发生扩散,不超限,加速网络拟合,增加网络的鲁棒性。
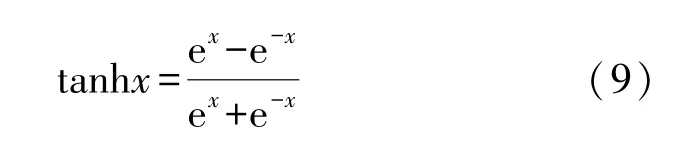
2.2 K-means模型更新算法
使用K-means模型更新算法可以使异常检测算法在遇到数据分布变化时(如出现数据波动、出现训练集中没有的数据分布),及时更新模型的权重,使其学习到新的数据分布。
K-means模型的输入与C-LSTM模型的输入相同。使用K-means将数据聚类为4个簇C={c1,c2,c3,c4},并获取其四个聚类中心CenterP={cp1,cp2,cp3,cp4},并将其中包含数据数量最少的簇ci设置为异常簇,其余簇设置为正常簇。若存在多个包含数据数量最小的簇,则计算各聚类中心到其余簇聚类中心的合向量的模VectorMod={vm1,vm2,vm3,vm4},并将所有包含数据数量最小的簇中合向量的模最大的簇设置为异常簇,其余簇设置为正常簇。据此,获取新的簇的集合{CP,CN},其中CP为异常簇,CN为正常簇,由此获得K-means的分类标签YK-means。
定义1(合向量的模)各聚类中心cpi到其余聚类中心的合向量的模vmi定义如下:
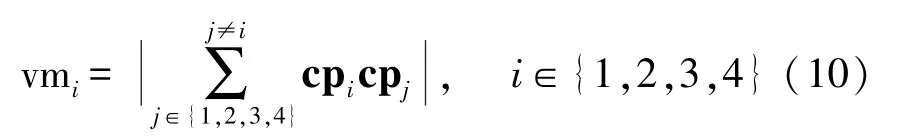

算法1 用K-means获取分类标签
定义2分类误差ε是指,C-LSTM分类结果Yclstm和K-means分类结果YK-means不同的数据的个数。

分类误差的阈值g根据经验值选取10。如果分类误差大于阈值g,则认定C-LSTM分类器分类结果不可信,并执行网络更新步骤;若分类误差小于阈值g,则认定C-LSTM分类器分解结果可信,并将其结果作为输出。
本文提出的C-LKM算法网络更新,仅更新CLSTM网络中的LSTM网络。更新方法包含有标注数据生成以及网络更新两部分。
有标注数据生成方法如下:
首先,认定C-LSTM和K-means分类所得标签Yclstm与YK-means相同部分对应的数据为可信数据,并对其进行标注;之后,利用K-means算法对不可信数据以k=2进行再次聚类,并将聚类所得簇中,数据量少的认定为异常簇,数据量多的认定为正常簇,并对其进行标注;之后将标注好的数据合并,作为CLSTM网络的输入,重新分类。

算法2 标注数据
网络更新方法如下:
将新生成的有标注数据输入预训练的CNN提取数据的高维特征,并将提取好的特征作为LSTM网络的输入;之后,利用反向传播不断更新LSTM网络的参数,直到LSTM网络的输出经全连接层以及Softmax分类器分类结果同原始有标注数据误差小于分类误差阈值g时,结束迭代,此时异常检测模型成功学习到新的数据分布;若迭代次数超过20次,结束迭代,此时异常检测模型未能学习到新的数据分布。至此,网络更新结束。这样可以有效避免因为数据分布变化带来的异常检测误报率上升、检测精度下降的问题。
C-LKM算法在检测时不断以最新获取的分类误差较大的数据作为网络输入重新训练LSTM网络,使其记住最新数据的时间特征。
2.3 本文提出的算法(C-LKM)
正常情况下,传感器网络采集的数据变化平缓,当异常发生时,某个传感器的数据会表现为较大的波动,当某些传感器的数据超出阈值时,判定为异常。异常可以分为三个类别,孤立点异常、上下文异常、集体异常[4]。这些异常发生时对应的特征波动相对稳定,但是也会出现预先没有学习到的异常特征波动。这是设计C-LKM的传感器数据流异常检测模型的原则。C-LKM的模型结构如图2所示,整个模型分为预训练与在线检测两大部分。该模型中,程序首先使用有标注的传感器数据流,对CLSTM网络进行预训练,获取预训练的C-LSTM网络,我们称之为预训练过程。在线检测过程中,模型接收并分类无标注的传感器数据,并使用K-means无监督的优化C-LSTM网络,修正模型误差。

图2 C-LKM的模型结构图

算法3 传感器数据流在线异常检测算法(C-LKM)
C-LKM模型既考虑了传感器数据流的空间相关性,也考虑了其时间相关性,并利用K-means算法实现了模型的半监督学习,模型在使用时,只需要少量数据进行预训练,实际预测中,便可依照数据特征,自动调节网络参数,使得模型可以有效分类新型异常数据。
3 实验与结果分析
3.1 实验环境
本文实验在一台安装了一块AMD R72700x CPU,一块NVIDIA GTX1080Ti GPU,32GB 2666MHz DDR4内存的电脑上完成。AMD R72700x CPU有8个核心,16个线程,能方便地训练与运行C-LKM模型,以及本文使用的各种对比模型;32GB内存则能保证存储全部的模型参数。程序运行在Windows10系统,使用numpy 1.18.0以及pandas 0.23.4进行数据预处理以及矩阵运算,使用tensorflow2.0.0利用CPU训练及运行网络模型。
3.2 数据集
为验证本文提出算法的可行性,使用英特尔伯克利研究室(IBRL)传感器数据集进行实验验证。该数据集是英特尔伯克利研究室(IBRL)在2004年2月28日至2004年4月5日收集的54个传感器的真实数据。该网络中,传感器每隔31 s收集一组包含温度、湿度、光照强度、传感器节点电压4个属性的数据[18],传感器网络中的节点分布如图3所示。选取31号节点数据作为本文实验原始数据。

图3 英特尔伯克利研究室(IBRL)传感器布置图
英特尔伯克利研究室传感器数据流为无标注的原始采集数据,数据中存在缺失值、异常值,在使用它进行实验之前需要对数据进行预处理。首先,因为采用的31节点前40000组数据中丢失数据均为该时刻全部的温度、湿度、光照以及电压数据,且只存在两段长时间的数据丢失情况。所以,忽略长时间丢失数据的情况,并对其余缺失值使用线性插值法[19]进行补齐,取补齐后数据的前60000组数据作为实验数据集,并将预处理后的数据标记为正常数据。
之后,对数据插入异常点。在实验数据集中,随机选取一些正常点,将其四个属性值改为异常值[20]。异常值计算方法为,以随机选取的异常点为中心,以15为时间窗口,计算该时间窗口内各属性的均值,以及方差μi={μti,μhi,μli,μvi},其中分别表示第i个时间窗口内,温度、湿度、光照强度、电池电压的均值;{μti,μhi,μli,μvi}分别表示第i个时间窗口内,温度、湿度、光照强度、电池电压的方差。异常值X′i的计算方法为:
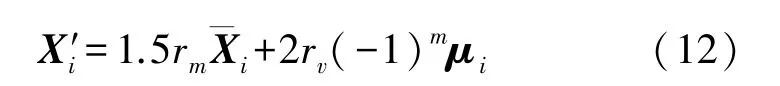
式中:m为计算机生成的随机数,m为正整数,rm和rv为取值在(0,1]内的随机数。实验中,分别向IBRL_31数据集中插入1%、2%、5%、10%的异常点,获取四组异常占比分别为1%、2%、5%、10%的有标注数据集,实验数据集如表2所示。
表2 实验数据集
3.3 评价指标
本文将异常检测作为二分类问题进行解决,最终分类结果为:异常P、正常N。对于二分类问题,将最终分类结果划分为:真正例TP(True Positive)、假正例FP(False Positive)、真反例TN(True Negative)、假反例FN(False Negative),其中正例P为异常数据,反例N为正常数据。异常检测数据集存在正反例占比不均的问题,为准确反映各对比模型的异常检测性能,采用召回率Recall、精确率Precission、F1-Score作为算法的评价指标。

使用算法方差变化率Rvar检测K-means模型更新算法对模型预测稳定性的提升效果。
定义3算法方差变化率Rvar:

式中:Varr为未用模型更新算法的异常检测算法异常检测结果的方差;Vars为使用模型更新算法后,半监督异常检测模型异常检测结果的方差。
3.4 实验结果与分析
为验证本文算法在长时间范围上的有效性,在补齐缺失值的IBRL_31数据集中选取60000组数据,分别插入占比1%、2%、5%、10%的异常点,以前5000组数据作为训练集,后55000组数据作为训练集进行试验。并且记录模型在每5000组测试数据上的异常检测准确性。分别用CNN、LSTM、CLSTM、CKM、LKM以及C-LKM在这三组异常占比不同的数据集上进行试验,其中CKM、LKM分别为CNN、LSTM应用K-means模型更新算法的半监督异常检测模型。使用召回率和F1-Score作为衡量指标,对比其检测精度,并计算算法在测试集11个不同时间段上检测结果的召回率以及F1-Score的方差,来验证K-means模型更新算法对异常检测模型检测稳定性的提升效果。
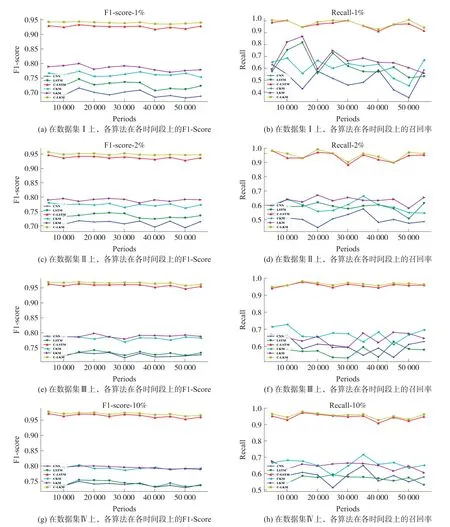
图4 CNN、LSTM、C-LSTM、CKM、LKM、C-LKM算法在各时间段上的F1-Score和召回率
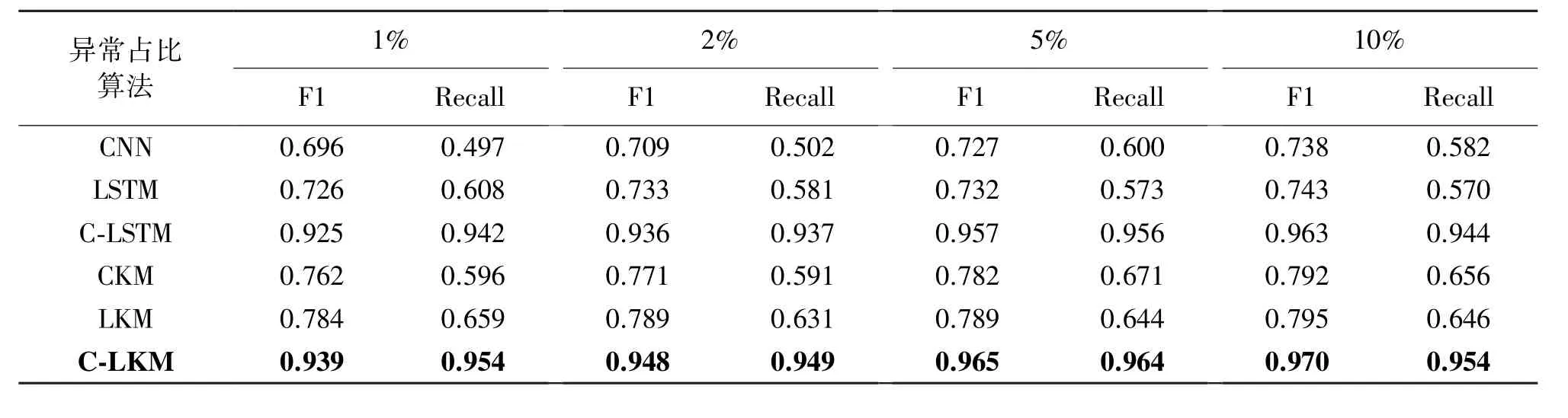
表3 算法在不同异常占比数据集上的F1-Score和Recall
实验结果如表3和图4所示,图4横坐标表示测试区间。由图4可知,C-LKM方法较C-LSTM方法在F1-Score和召回率上有明显提升。当异常占比为1%时,C-LKM在每一段测试集上的F1-Score最高为0.942,召回率最高为0.983,在全部55000组数据上的F1-Score均值为0.939,召回率均值为0.954。当异常占比为2%时,C-LKM在每一段测试集上的F1-Score最高为0.956,召回率最高为0.989,在全部55000组数据上的F1-Score均值为0.948,召回率均值为0.949。当异常占比为5%时,C-LKM在每一段测试集上的F1-Score最高为0.968,召回率最高为0.980,在全部55000组数据上的F1-Score均值为0.965,召回率均值为0.964。当异常占比为10%时,C-LKM在每一段测试集上的F1-Score最高为0.976,召回率最高为0.977,在全部55000组数据上的F1-Score均值为0.970,召回率均值为0.954。相较于其他对比算法,C-LKM算法提升了异常点检测准确度。对比未使用K-means模型更新算法的原算法,使用K-means模型更新算法之后,模型在各区间上的F1-Score和召回率均获得明显提升,其中,K-means模型更新算法对CNN以及LSTM算法提升最明显。这是由于单独的CNN无法有效提取传感器数据流的时间特征,单独的LSTM算法无法有效提取传感器数据流的空间特征,这导致预训练期间,他们的模型无法有效拟合。随着输入数据增加,K-means模型更新算法可以利用新获取的传感器数据继续训练预训练模型,帮助模型进一步拟合,从而提升模型异常检测效果。C-LSTM算法本身已经可以有效提取传感器数据流的时空特征,在预训练阶段已经获得了较好的拟合效果,但是由于训练集数量较少,只有5000组数据,并且训练集异常占比低,异常种类不全,导致模型并未完全拟合。之后,K-means模型更新算法依旧可以利用新获取的传感器数据流继续训练模型,使得模型进一步拟合,提升了模型异常检测效果,但是提升幅度没有前两种模型高。

图5 CNN、LSTM、C-LSTM、CKM、LKM、C-LKM算法在各数据集分组上的F1-Score和召回率箱型图
为探究K-means模型更新算法对异常检测算法异常检测效果及稳定性的提升,以及对比异常检测算法在不同异常占比的数据集上的异常检测效果,使用各异常检测算法在测试集11个时间段上异常检测结果的召回率以及F1-Score作为元数据,绘制箱型图。图5展示了各对比算法在各实验数据集分组上的F1-Score和召回率箱型图。其中箱体内部的线表示异常检测算法在测试集11个时间段上异常检测结果的召回率以及F1-Score的中位数,箱体部分表示实验结果第1四分位至第3四分位的数值范围,三角形表示实验结果的均值。箱体部分范围越窄,实验结果越集中。从图上可以看出,使用K-means模型更新算法之后,异常检测结果的F1-Score和召回率均获得提升,并且实验结果分布更集中,表明随着新数据输入异常检测模型,模型成功学习到了新型异常的特征,并检测出了新型异常,这提升了模型的检测稳定性。随着异常数据占比的提升,异常检测算法在测试集11个时间段上异常检测结果的召回率以及F1-Score的分布,呈集中趋势,以及上升趋势,这表明,异常数据占比越高,异常检测算法的异常检测效果越稳定,异常检测准确度越高。这是由于随着异常占比的提升,异常检测数据的数据分布更为理想(二分类问题理想类别比例为1∶1),模型训练时可以学习到更多的异常类别的特征,以及正常类别的特征,模型拟合的更好。
进一步,使用原异常检测算法以及使用Kmeans模型更新算法后的异常检测算法在每一段异常检测数据集上F1-Score的方差变化率和召回率方差变化率,量化K-means模型更新算法对异常检测结果稳定性的提升效果。图6所示为各算法的F1-Score和召回率在每一段测试集上的方差。表4展示了K-means模型更新算法对异常检测结果稳定性的提升效果。从表中可以看出,使用K-means模型更新算法之后,F1-Score最高提升了73.1%,召回率最高提升了31.1%,并且对F1-Score稳定性的提升远高于对召回率稳定性的提升。由于F1-Score是综合了准确率和召回率的评价指标。因为异常检测数据集中,异常占比低,即使将所有数据全部检测为正常数据,获取的准确率也高于90%。原算法的F1-Score波动较大说明原算法的误报率(FPR)不稳定,原算法的异常检测准确率受正常数据在短时间范围内的波动影响较大,这也是由训练集在总数据集上占比小,无法反映完整数据集的数据分布导致的[21]。K-means模型更新算法使原算法在数据流发生波动时及时调整权重,来适应数据流在短时间范围上的波动,并且在遇到未学习到的数据分布时及时调整权重,从而学习到了新的数据分布。表4中部分Recall的稳定性变化率为负值,这表明在全部的测试结果中,召回率的稳定性存在变坏的情况。这由两种情况导致:①模型重训练时存在过拟合的可能;②K-means模型更新算法将占比最少的簇设置为异常簇,这使得系统可以利用新的数据流重新训练异常检测模型,但是这种分类方法不完全可信,可能将某些正常数据划分成异常数据,导致模型向相反的方向训练,最终使得召回率稳定性下降。
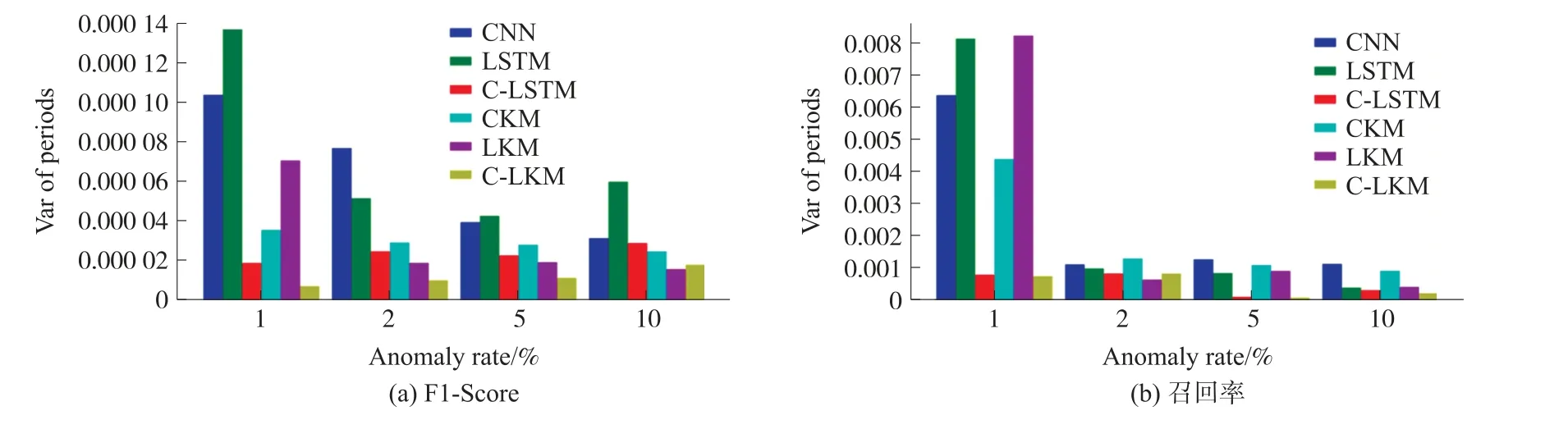
图6 各算法的F1-Score和召回率在每一段测试集上的方差

表4 K-means模型更新算法对异常检测结果稳定性的提升 单位:%
为探究K-means模型更新算法对检测时间上的影响,本文统计并分析CKM、LKM以及C-LKM在线检测阶段(使用测试集)触发模型更新的次数,以及模型更新所用的时间,得出的结论如表5所示。其中触发次数指的是在线检测阶段各实验模型触发模型更新的次数;平均时间指的是完成一次模型更新使用的平均时间,单位是毫秒(ms);失败次数指的是在一次模型更新中,模型经历20次迭代之后,其分类误差依旧超过阈值的次数。模型更新失败代表着模型没有学习到近期数据的有效特征。从表5可以看出,三种使用了K-means模型更新算法的模型在在线检测阶段均触发了模型更新机制,其中CKM、LKM由于其原始算法CNN、LSTM的检测准确度低,其触发模型更新机制的次数也很高,其模型更新的失败次数也很高说明了这两种算法的可以有效的学习到新数据的特征,但是受限于原始模型的性能,其无法准确学习到新数据的特征。C-LKM的模型更新机制触发次数很少,模型更新失败次数也很少,说明其可以有效并准确地学习到新数据的特征。同时,三种模型在本实验平台上,模型更新速度都是毫秒级,实际应用中不会造成性能瓶颈。
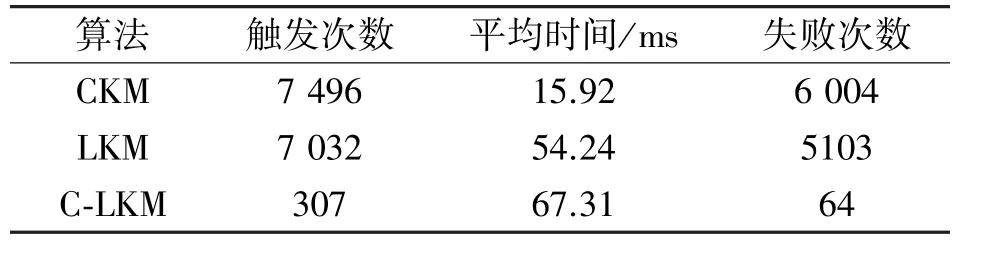
表5 模型更新机制统计结果
4 结论
本文提出了一种针对到达服务器端的环境监测传感器数据流在线异常检测的半监督学习方法,该方法只需要少量的有标注数据集作为训练集,所提的K-means模型更新算法可以提高原算法在长时间范围上的检测准确度以及检测稳定度。在本实验平台上,C-LKM算法对于单一节点数据的平均检测时间在毫秒级,对于以固定时间间隔上报数据的环境监测传感器网络的异常检测应用不会造成性能上的瓶颈。本研究的实证结论对将现有的有监督异常检测模型转变为半监督模型提供了一种参考。

