一种非极限状态主、被动土压力计算方法
曹海莹,张书恒,费兴彪,刘德用
(1.燕山大学 河北省土木工程绿色建造与智能运维重点实验室,河北 秦皇岛 066004; 2.燕山大学 建筑工程与力学学院,河北 秦皇岛 066004)
0 引言
随着道路工程的不断发展,支挡结构被越来越多地运用于陡坡路基条件下,在挡墙发生过移动后的土压力计算是否仍能按照极限状态土压力进行计算已经引起了越来越多的关注[1]。经典的土压力理论因其简单实用,一直被沿用至今,但在工程实际中,土体发生的位移很小,往往处于一种非极限状态[2],经典的郎肯理论和库伦理论已不能满足实际工程的需要,因此,研究非极限状态下的土压力计算模型,有着非常重要的意义。
目前研究非极限状态下的土压力问题,可归纳为以下4种途径:现场监测[3-4]、模型试验[5-7]、数值模拟[8-10]和理论计算[11-15]。文献[3-4]通过对挡墙实体工程的现场原位监测, 研究分析了挡土墙后土体垂直土压力、墙背侧向土压力分布规律。文献[5-7]通过土工离心模型试验、现场缩尺模型试验等研究讨论了挡墙不同位移模式下墙背土压力和路基填土变形的影响关系,分析了刚性变位模式下挡墙土压力的变化,得到了墙背土压力的基本规律。文献[8]进行了有限元模拟,以研究砂土的三维主动土压力,分析了变形模式、长宽比、相对密度和墙土摩擦角对土压力-位移的影响。文献[9-10]通过模型试验和数值模拟相结合的方法,研究了土体位移随填土高度的变化规律和土压力的分布特性。
理论计算大致可归为以下几类:第1类是考虑非极限土压力与填土位移的关系,建立土压力与位移之间的函数关系式[11-13]。此类方法抓住了土压力大小主要取决于填土位移这一关键问题,其缺点是两者的函数关系式很难统一。第2类是考虑了土体在运动过程中自身参数从初始值到极限值的发挥过程,用非极限状态下的土体参数替换经典土压力计算理论中的土体参数[14-16]。此类方法使用了土的抗剪强度发挥值的概念,思路清晰,不足之处在于缺乏揭示土体强度参数与位移之间非线性关系的实测数据。第3类是通过改进的库仑极限平衡理论,利用薄层单元法开展非极限状态土压力计算[17-18]。此类方法推导过程严密,但因涉及的计算参数众多,目前适合复杂工况的理论公式并不多见。理论计算方法中的这几种思路在一定程度上解决了非极限土压力的计算问题,推动了相关研究的发展,但也存在着计算误差较大、过程繁琐的弊端。
虽然已有的关于非极限土压力的研究有了较大的进展,但其理论研究仍处于不成熟阶段,还需进一步深入。本研究基于非极限土压力与静止土压力和极限土压力的关系特性,在文献[11]的基础上,运用加权组合的数学思想,结合已有非极限土压力的研究成果,提出一种简单实用、计算结果准确的非极限土压力计算模型,并与已有方法比对验证,证明该模型的合理性。
1 加权组合计算模型
在支护结构中,当位移为0时,土体处于静止状态,此时的土压力为静止土压力;由于某种原因导致支护结构产生偏离或偏向土体的位移时,会使得水平应力衰减或增长,直至土体达到极限平衡状态,衰减和增长的土压力分别称为松弛应力和挤压应力[11],静止状态与极限状态之间的“中间状态”称为非极限状态,相应的土压力为非极限主动土压力或非极限被动土压力。
在相同条件下,静止土压力、非极限土压力、极限土压力之间存在如下关系:
(1)
(2)

非极限土压力可用如下形式表示[11]:
(3)
(4)
式中,pr为松弛应力;ps为挤压应力。
对式(3)变形为:
(5)
由式(1)、式(5)可得,最大松弛应力prmax为:
prmax=p0-pa。
(6)
显然,非极限主动土压力的大小取决于松弛应力的大小,松弛应力大,则非极限主动土压力小;松弛应力小,则非极限主动土压力大。因此,可以引入一个反映松弛应力大小对非极限主动土压力影响程度的参数。卢坤林等[12]通过引入位移函数来描述松弛应力与其最大值之间的关系,但考虑到函数模型的普适性以及模型参数的不确定性,在非极限土压力的计算中仍有诸多不便。
引入松弛应力发挥系数w:
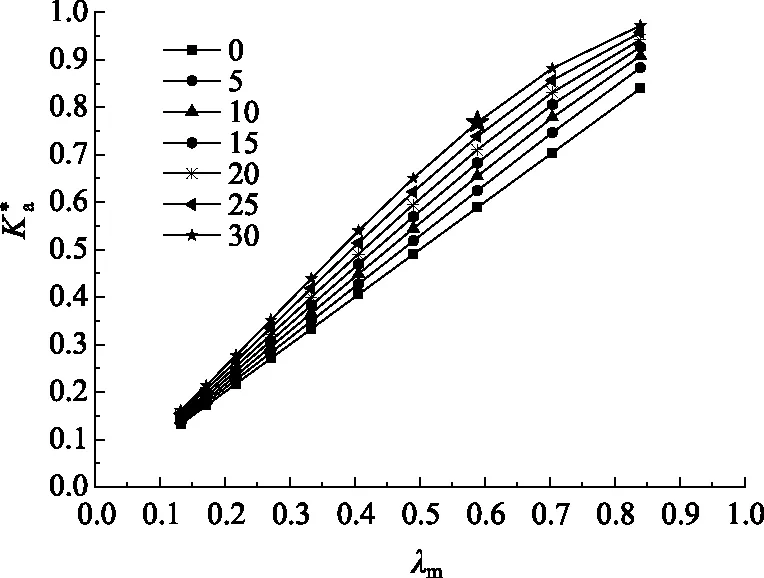
(7)
将式(3)、(6)代入式(7)可得:
(8)
由式(1)、(8)可知:0≤w≤1。
松弛应力发挥系数体现的是应力松弛程度的大小,反映了松弛应力大小对非极限主动土压力的影响程度,由式(8)知,松弛应力发挥系数越大,应力松弛程度越大,非极限主动土压力越小。当w=0时,土体未发生松弛,即处于静止状态;当w=1时,土体完全松弛,达到主动状态;当0 (9) 式(9)即为基于松弛应力发挥系数的加权组合计算模型。 经典的土压力理论中,对无黏性土,土压力可表示成如下形式: pa=Kaγz, (10) p0=K0γz, (11) 式中,K0为静止土压力系数;Ka为主动土压力系数;γ为填土重度;z为所计算点到填土面的高度。 当土体处于非极限状态时,作如下假定:(1) 挡土墙后填土为无黏性土;(2)土体处于非极限状态时,土体中存在潜在的滑动面;(3)填土表面无超载。 依据上述假设,非极限主动土压力可表示为如下形式[17]: (12) 把式(10)~(12)代入式(8)可得: (13) 文献[17-18]通过薄层单元法研究了挡土墙非极限状态下的主动土压力,推导了非极限状态下各参数的表达式,在上述研究的基础上,通过推导非极限侧土压力系数与摩擦角的关系,提供一种简单实用的非极限主动土压力计算方法。以文献[17]中推导的公式为计算依据: (14) 其中: (15) (16) 式中,α,β分别为墙背的倾斜角、墙后填土面的倾角;φm,δm分别为非极限状态下的土体内摩擦角、墙土摩擦角;θ为准滑动面与水平面倾角。 当α=0,β=0时,对式(14)~(16)作简化: (17) (18) (19) 当墙背光滑,即δm=0时,作进一步简化可得: sq=1, (20) (21) (22) (23) 因此,在α=0,β=0,δm=0时, (24) 图与λm关系图Fig.1 Relationship between and λa 用Matlab拟合函数关系,如表1所示。 表与λa关系表 (25) 作m,b这两个参数与sinδm的关系图,如图2、图3所示。 图2 m与sin δm关系图Fig.2 Relationship between m and sin δm 图3 b与sin δm关系图Fig.3 Relationship between b and sin δm 按线性关系处理时,相关系数为0.981 9。用Matlab拟合可得如下关系: m=0.371sinδm+1.021 6。 (26) 在Matlab中用二次函数拟合: b=0.184 7(sinδm)2-0.031 4sinδm-0.001 9。 (27) 文献[12]通过研究应力-应变关系,建立了非极限内摩擦角与位移的关系。 sinφm= (28) 式中,φ为主动极限状态时的填土内摩擦角;η为位移比,η=s/sc(s为位移,sc为达到极限状态时的位移),r为破坏比,取值0.75~1.0。 假设墙土摩擦角与内摩擦角有相同的变化规律,则: sinδm= (29) 式中δ为极限状态时的墙土摩擦角。 表2 非极限主动侧土压力系数 在式(28)中: K0=Kη=0。 (30) Ka=Kη=1。 (31) 引入挤压应力发挥系数ζ: (32) 式中psmax为最大挤压应力。 同理可得到基于松弛应力发挥系数的加权组合计算模型: (33) ζ可按照下式计算: (34) 对于非极限被动土压力,仍可采用与非极限主动土压力类似的计算模型来进行计算,即:使用加权组合的数学思想来计算非极限被动土压力。同理,非极限被动土压力的大小跟挤压应力的大小有关,挤压应力大,则非极限被动土压力大;挤压应力小,则非极限被动土压力小。因此,引入一个反映挤压应力大小对非极限被动土压力影响程度的参数,即挤压应力发挥系数。 主动非极限状态和被动非极限状态是土体运动过程中的两个相反的过程,因此,把主动非极限状态下计算公式中的相关参数(φm,δm)取相反数[19],即可得到非极限被动状态下的计算公式。当α=0,β=0时: (35) (36) (37) 当墙背光滑,即δm=0时,作进一步简化可得:sq=1。 (38) (39) (40) 因此,在α=0,β=0,δ=0时, (41) 图与λp关系图Fig.4 Relationship between and λp 在图4中,与线性关系明显,按照线性关系处理时其相关系数大于0.98,用Matlab拟合函数关系,如表3所示。 表与λp关系表 (42) 图5、图6分别为n、c与sinδm的关系图。 图5 n与sin δm关系图Fig.5 Relationship between n and sin δm 图6 c与sin δm变化关系图Fig.6 Relationship between c and sin δm 用Matlab拟合图中关系可得: n=5.811 6(sinδm)2-2.571 4 sinδm+1.007 5。 (43) 用Matlab拟合图中关系可得: c=-9.625 7(sinδm)2+3.524 7sinδm-0.036 1。 (44) 徐日庆等[20]提出了非极限状态摩擦角从静止状态到极限状态随墙体位移变化的计算公式: tanφm=tanφ0+Kd(tanφ-tanφ0), (45) tanδm=tanδ0+Kd(tanδ-tanδ0), (46) 式中,Kd为考虑s对φm和δm影响的系数,Kd=4arctanηπ;δ0为静止状态时的墙土摩擦角,δ0=φ/2。 K0=Kη=0。 (47) Kp=Kη=1。 (48) 表4 非极限被动侧土压力系数 当挡土墙位移为0时,土体处于静止状态,图7所示为本研究方法、经典理论(为简化计算,采用摩擦角代替有效摩擦角,因此,计算结果偏小)与贾宁法[21]对静止土压力系数的计算结果比较。 图7 K0计算结果比较Fig.7 Comparison of calculation results of K0 由图7可知,3种方法的计算结果比较相近,当摩擦角较小时,本研究方法的计算结果略大于贾宁法和简化后的经典理论计算结果,随着内摩擦角的增大,贾宁法越来越接近本研究方法,而两种方法的计算结果与经典理论的计算结果都相差较小,因此用本研究方法来计算静止土压力也能得到比较理想的结果。 当挡土墙向离开土体方向发生位移达到极限状态时,土体处于主动状态。图8所示为本研究方法与库仑理论和朗肯理论在计算主动土压力系数时的比较结果。 图8 Ka计算结果比较Fig.8 Comparison of calculation results of Ka 由图8可知,本研究方法计算结果大于朗肯理论和库仑理论的计算结果,而朗肯理论忽略了墙背与填土之间的摩擦,本身就会使计算结果较大,因此,采用本研究方法计算主动土压力时会带来较大的误差。 当挡土墙向土体方向发生位移达到极限状态时,土体处于被动状态。图9所示为本研究方法与朗肯理论、库仑理论在计算被动土压力系数时的比较结果。 图9 Kp计算结果比较Fig.9 Comparison of calculation results of Kp 由图9可知,本研究方法与朗肯方法计算结果较为相近,库仑理论在计算被动土压力时会带来较大的误差。当摩擦角较小时,本研究方法计算结果略小于朗肯理论,随着摩擦角的增大本研究方法的计算结果会略大于朗肯理论,而朗肯理论在计算被动土压力时会偏小,因此,在土体的摩擦角较大时,采用本研究方法计算被动土压力会得到更为理想的结果。 4.2.1 非极限主动土压力 Fang[22]试验的试验条件如下:刚性挡土墙墙背直立,墙高h=1.0 m,填土为干砂,填土面水平无超载,γ=15.4 kN/m3,内摩擦角φ=34.0°,取δ=2φ/3,r=0.85,进行分析计算时分别取η=0.1、η=0.2。图10为本研究计算结果、卢坤林方法[12]与试验实测结果的比较。 由图10看出,3种方法对非极限土压力的计算中,土压力变化呈现一致的规律,即随深度的增加土压力增加,随位移的增加土压力减小。但本研究方法与实测值的误差更小,优于卢坤林法,且本研究计算出的非极限土压力是非线性变化的,与实测结果一致。 图10 理论计算值与试验结果比较Fig.10 Comparison of theoretical calculation value and test result 岳祖润[23]试验的试验条件如下:离心模型试验中采用压实黏土,模型箱净空25 cm×31 cm×41.5 cm。土体参数如下:γ=18.7 kN/m3,c=38.2 kPa,φ=22.7°,取δ=2φ/3,r=0.85。图11、图12分别为p16、p17测点土压力本研究计算值、卢国胜方法[24]计算值与实测值的比较。 图12 理论计算值与试验结果比较(p17)Fig.12 Comparison of theoretical calculation value and test result (p17) 由图11、图12可以发现,在挡土墙某一高度处,随着挡土墙位移的增加,非极限主动土压力呈非线性减小,本研究方法与卢国胜法[24]的规律是一致的。在静止状态和主动状态时两种方法的计算结果均与实测值相同,但在非极限状态时,本研究的计算值与实测值吻合更好,两者之间误差极小,优于卢国胜法,更适用于非极限状态下主动土压力的计算。 虽然在非极限土压力计算模式中所涉及的系数推导,存在着假设条件,但最后推导出的非极限土压力计算模型中,只涉及到了摩擦角的变化过程。因此,无论是砂土还是黏性土,有无超载,以及填土面倾角等条件可能并不影响非极限土压力的计算,在上述岳祖润[23]试验实例验证中也说明了这一问题,当然这也需要更多理论和实例的支撑。 4.2.2 非极限被动土压力 Fang[25]试验:针对不同类型的砂土做了模型试验,表5为试验的相关数据。填土表面水平,墙高0.5 m。采用本研究方法分别计算了不同位移条件下相对密度(Dr)为38%,63%时砂土水平土压力随深度的变化值,并与试验数据和杨泰华等方法[26](以下简称“文献方法”)作了比较,如图13、图14所示。 表5 试验数据 图13 理论计算值与试验结果比较(Dr=38%)Fig.13 Comparison of theoretical calculation value and test result (Dr=38%) 图14 理论计算值与试验结果比较(Dr=63%)Fig.14 Comparison of theoretical calculation value and test result(Dr=63%) 由图13、14可知,当挡土墙位移较小时,本研究方法与文献方法的计算结果都与实测值接近,能够很好地估算非极限状态下的被动土压力,但当位移较大时,文献方法与实测值的误差增大,给非极限被动土压力的计算带来较大误差,而本研究方法的误差较小,更适用于计算非极限状态下的被动土压力。 (1)基于加权组合的数学思想,建立了一种非极限状态主、被动土压力计算方法,该方法考虑了非极限状态侧土压力系数与土体内摩擦角、墙土摩擦角的非线性关系;相比极限平衡状态下经典土压力计算方法,非极限状态土压力计算方法更适用于实际工况,具有重要的工程应用价值。 (2)静止土压力、极限状态土压力是非极限状态土压力的两个边界,这为加权组合计算模型的构建提供了前提条件;通过引入松弛应力发挥系数、挤压应力发挥系数为加权组合计算模型在土压力计算中的应用提供了实现路径。 (3)非极限状态侧土压力系数由于未考虑层间剪应力相互作用,导致本研究计算方法的精度仍有提高的空间;通过考虑墙土摩擦效应,提高了非极限土压力计算精度,但墙土摩擦角计算结果与实际工况仍存在差异,若能进一步探明墙土摩擦效应规律,并建立墙土摩擦角计算公式,非极限土压力的计算结果会更加精准;对于实际工况下侧土压力系数、墙土摩擦角的现场监测是未来关注的重点。2 非极限主动土压力计算
2.1 松弛应力发挥系数的引入
2.2 松弛应力发挥系数的推导






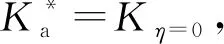

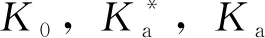
3 非极限被动土压力计算
3.1 挤压应力发挥系数的引入

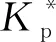
3.2 挤压应力发挥系数的推导

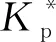




4 验证分析
4.1 边界条件验算

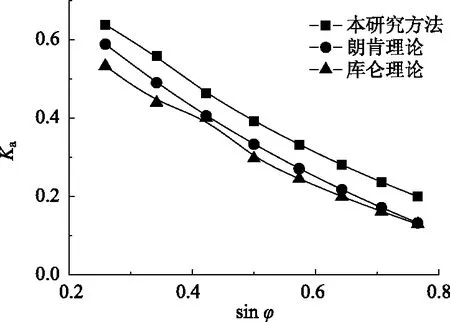

4.2 实例验证

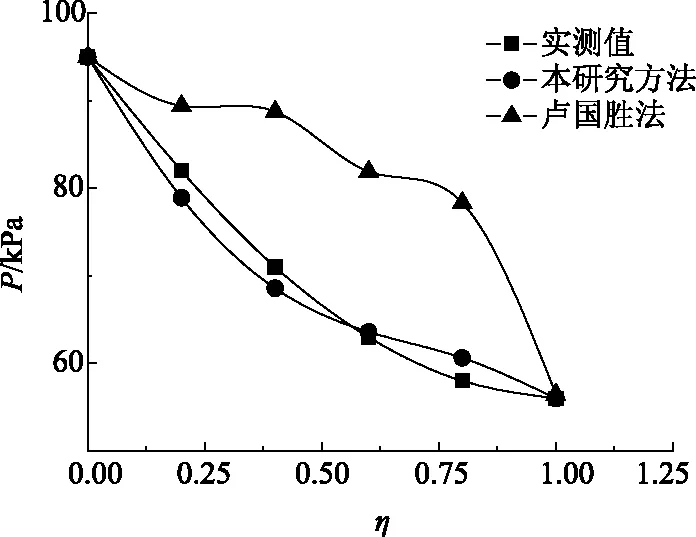

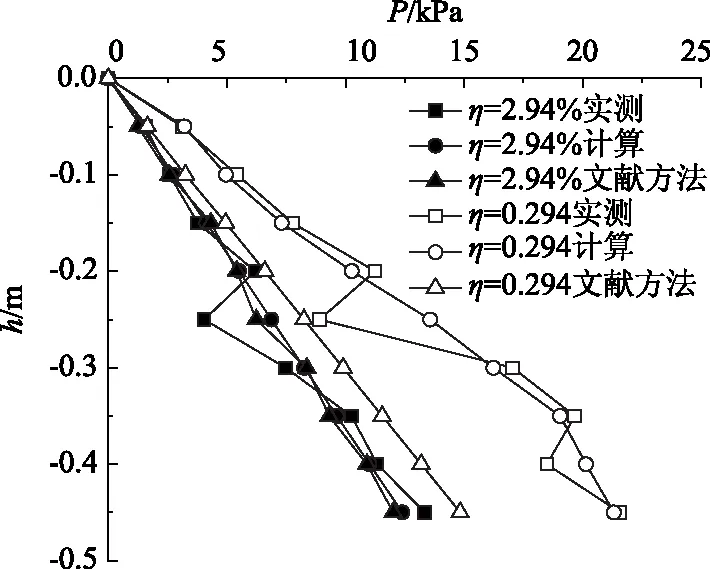
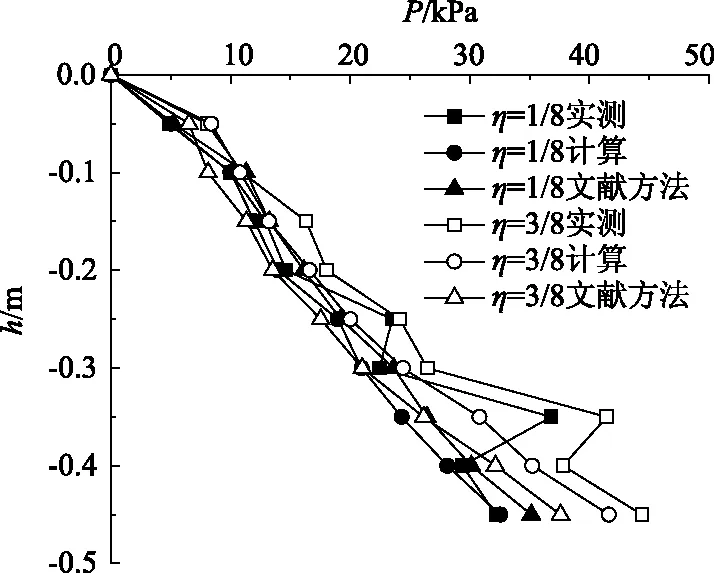
5 结论

