缺失数据条件下基于GAN与LSTM的水文预报研究

秦 鹏，陈 雨，卢文龙

（1.四川大学 电子信息学院，四川 成都610065；2.成都万江港利科技股份有限公司，四川 成都610041）

水文预报［1］旨在根据某一区域或某一水文站的历史水文气象数据对河流水文情势进行定性或定量预测，是防洪调度决策、生态环境保护、水资源综合开发利用等的重要依据。水文预报方法可分为传统方法和新方法两大类。传统的中长期预报方法主要是根据河川径流的变化具有连续性、周期性、地区性和随机性等特点来开展研究，主要有成因分析和水文统计方法［2］。ARIMA模型［3］的基本思想是通过差分消除序列中的趋势项，将非平稳序列转化为平稳序列，逐渐应用于水文预报［4-5］；李亚伟等［6］提出的SVR模型建立在VC维概念和结构风险最小化原理基础上，根据有限的样本信息在模型的学习精度和学习能力之间寻求最佳组合，也成功应用于水文预报。近年来，随着计算机技术的发展和新的数学方法的不断涌现，针对复杂的水文水资源时间序列问题，具有极强的自适应学习能力和非线性映射能力的深度神经网络方法应运而生，如人工神经网络（ANN）、递归神经网络（RNN）、卷积神经网络（CNN）以及长短时记忆网络（LSTM）。

水文数据是对大自然发生的水文情况实时、连续、长期观察记录的结果，具有序列性、实时性、海量性等特点。数据缺失在水文学研究中是一个常见的问题，其产生的原因多种多样，包括测量仪器的损坏、环境的干扰以及人工记录中的误差等［7］。数据缺失通常会降低水文模型统计分析的准确性［8］，甚至会造成对两个或多个变量之间的时序关系进行有偏的估计［9］。这两种问题（准确性骤降和估计偏差）都可能导致在分析存在数据缺失的数据集时受到极大的干扰，从而得出不正确的结论［10］。因此，水文数据的质量和完整性对于水文预报模型至关重要。

水文数据是典型的时间序列数据，为了解决时间序列预测模型因数据缺失而导致的精度、性能等问题，有关学者已经提出了多种方法。最早的解决方案是直接省略缺失数据，仅采用观测到的数据。但是当数据缺失较严重时，模型的性能将非常差。张升堂等［11］提出一种线性插值模型，该模型采用缺失数据站点邻近的3个位置生成一个时空插值平面进行线性插值。谢景新［12］提出由一系列已知观测点形成一条光滑曲线，通过求解三弯矩阵方程得出曲线函数组继而对缺失站点进行插值的三次样条插值法，但是无论是线性插值还是样条插值都仅仅是对缺失数据的一次平滑和近似拟合，无法挖掘到缺失数据的隐藏信息。王方超等［13］提出了一种调整最大似然法，不引入外部信息，根据数据自身的特性进行插值，是一种数据驱动估算法。此外还有基于回归的估算、基于主成分分析的数据估算等方法作为改进的插补方法被提出来，这些方法虽然改善了插值精度，提高了统计分析的准确性，但是仍然无法解决估计偏差的问题。水文数据是时间序列数据，其各个特征在时间序列上呈高度相关性，缺失值的估算应考虑水文数据的时间序列性质。

近年来，循环神经网络（RNN）中的长短时记忆网络（LSTM）和门控循环单元网络（GRU）在关于时间序列数据的应用上具有优秀的表现，例如机器翻译和文本识别。RNN可以通过反馈连接的时间延迟单元捕获输入序列的动态时间关系，学习水文系统的顺序或时变模式，展示了强大的预测性能。生成对抗网络（GAN）模型具有学习原始数据分布生成数据的特点，Goodfellow等［14］、王万良等［15］从理论上证明了当GAN模型达到收敛状态时，生成数据具有和真实数据相同的分布。笔者在存在缺失的水文数据集中引入GAN模型，把GRU作为生成器，把CNN作为判别器，通过对抗学习，为数据集中的缺失部分填充与真实数据分布一致的生成数据。该生成数据与真实数据分布趋于一致，而且可以表征缺失数据的时序特性，是高质量的填充数据。因此，GAN模型为上述问题提供了更好的解决方案。与此同时，将GAN模型与长短时记忆网络（LSTM）结合，提出了一种新的耦合模型GAN-LSTM（简称为GANL）。该模型由GAN和LSTM两个子模型耦合组成，首先通过GAN模型对数据缺失部分进行填充，整合出高质量的数据，解决目前水文预报中常见的数据缺失问题；然后通过GAN模型整合出的数据来训练LSTM模型，进行预测处理。该模型不仅有效改善了缺失数据的问题，而且可以捕获水文时间序列观测值的长期相关性，利用缺失信息来改善预测性能，从而有效地实现数据缺失条件下的水文预报。

1 生成对抗网络介绍

受博弈论中的二人零和博弈（two-player game）启发，Goodfellow开创性地提出了GAN模型。在二人零和博弈中，博弈双方的利益之和为零或一个常数，即一方有所得，另一方必有所失。GAN模型中的博弈双方分别由生成模型G（generative model）和判别模型D（discriminative model）组成，将随机变量作为生成模型的输入，经过其非线性映射，输出对应的信号作为判别模型的输入，由判别模型来判断该信号来自于真实数据的概率。在训练过程中，生成器努力地欺骗判别器，而判别器努力地学习如何正确区分真假样本，这样，两者就形成了对抗的关系，最终目标就是让生成器生成足以以假乱真的伪样本。GAN模型在计算机视觉领域已得到成功运用，如图像修复、语义分割和视频预测［16-18］。

2 模型设计

GANL模型（如图1所示）主要完成两方面的任务:一是学习数据分布、捕获缺失信息，生成缺失数据以整合出高质量的数据；二是将整合出的数据作为训练数据，训练预测模型、进行有效的水文预报。图1左半部分描述的是GAN模型，由生成器GRU和判别器CNN组成。将观测数据、缺失标志组成的联合向量作为生成器的输入，在经过GRU训练后形成一种新的特征表示，然后将新特征传入判别器CNN中，由判别器CNN来鉴别传过来的新特征分布是否与真实历史数据的分布趋于一致，如果一致则可以作为最终生成数据对缺失数据进行填充，继而作为图1右侧预测模型的训练数据，如果不一致则重新传回GRU层进行重复对抗训练。图1右侧描述的是LSTM模型，此部分模型输入的是由GAN模型传来的整合填充过的多变量时序数据（流量、降雨量、蒸发量等），输出是预测值（水位等）。

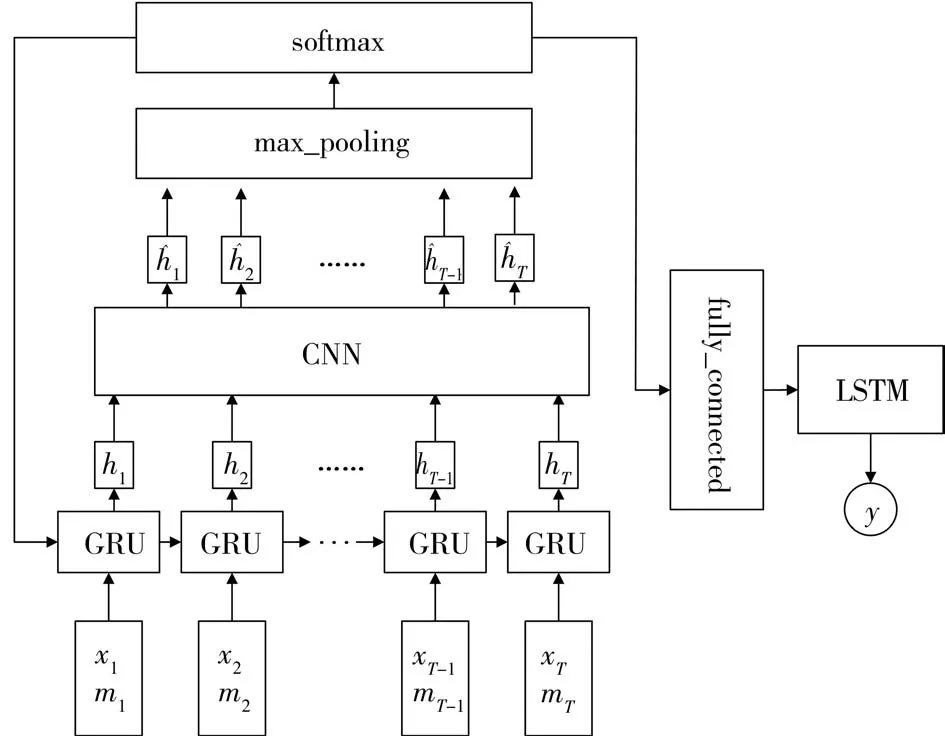
图1 GANL模型

2.1 GAN子模型

GAN模型包含生成模型和判别模型两个模块。生成模型接收随机信号作为输入，经过某种映射后又将输出信号作为判别模型的输入，由判别模型来判断该信号来自真实数据的概率。因此，两个模块的目标是完全相反的，生成模型的目标是最小化对数似然函数，使得输出信号与真实数据的分布趋于一致，而判别模型的目标则是用最大化对数似然函数判断输入信号是否来源于真实数据。利用GAN模型可以学习数据分布生成数据的特点，将观测数据和缺失标志组成的联合数据作为生成模型的输入，经过非线性映射将联合数据的特征分布传递给判别模型，然后由判别模型来判断生成的特征分布和真实数据的特征分布的异同，反复对抗训练直到判别器无法判断两者的区别，此时判别模型的输出结果就是要填充的缺失数据。CNN上面的max＿pooling层对CNN的输出特征进行降采样池化操作，softmax层判断新特征分布是否与原数据分布一致，fully＿connected层对特征空间维度进行转换以方便后续的预测。

2.1.1 GRU生成模型

用长度为T的D维向量表示一个多元时间序列水文数据，记为X=（x1，x2，…，x T），其中每一个时刻的x都有D个变量表示t时刻变量d的观测值。引入一个D维的缺失标志向量m t∈｛0，1｝D来表示t时刻的观测变量是否缺失。

GRU结构如图2所示，对于每个时刻的隐藏单元，GRU都有一个复位门r t和更新门z t来控制隐藏特征h t，更新方式如下:

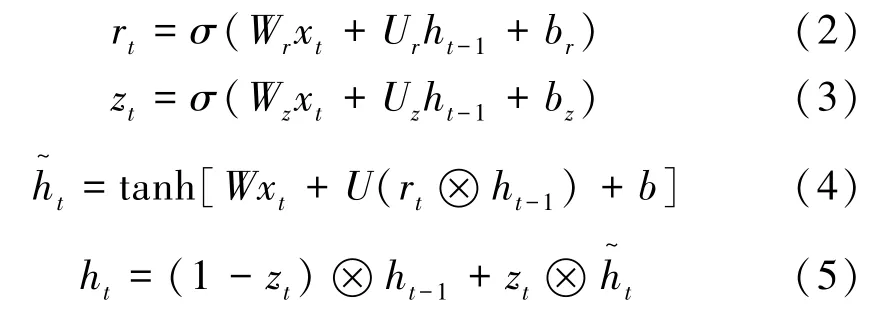
式中:W z，W r，W，U z，Ur，U和bz，b r，b均为可以学习的参数，表示连接各个门的权重；σ（）为Sigmoid函数；⊗为element-wise乘法（矩阵的对位元素依次相乘）。

图2 GRU结构

2.1.2 CNN判别模型

将卷积神经网络CNN作为判别模型，将GRU的输出结果h t转化为新的特征表示

式中:h t为GRU提取的特征为判别模型CNN生成的特征；Wc为CNN的模型参数。

接下来采用池化层提取重要特征，然后将提取出的特征输入到softmax层，根据映射的概率值来判断是否和原始数据分布一致。如果一致则可以作为整合数据通过全连接层输入到图1右边的预测模型中。

2.1.3 GAN模型目标函数

GAN模型的学习过程是生成模型和判别模型反复对抗训练的过程，两个模型的目标截然相反，本质上一个是最小化、另一个是最大化问题，这个最小最大优化目标表示如下:

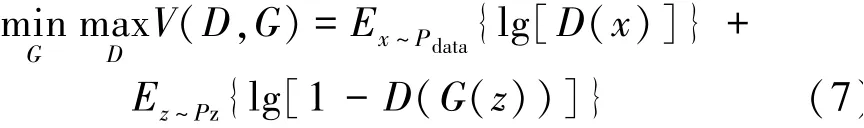
式中:D表示判别器；G表示生成器；D（x）为判别器的输出；G（z）为生成器的输出；Pdata为输入数据的分布；Pz为生成数据的分布；V为Pdata和Pz两个分布的jensen-shannon差异。

实际训练中，GAN模型收敛的过程是非常缓慢的。在GAN模型训练过程中，默认判别模型的判别能力比生成模型的数据生成能力强，这样判别模型才能指导生成模型朝好的方向学习，因此通常的做法是先更新判别模型的参数多次，再更新生成模型的参数一次。本文借鉴文献［19］的做法，分别为判别模型和生成模型设置不同的学习率，以加快判别模型的收敛速度。

2.2 LSTM子模型

水文数据是典型的时间序列数据，数据间有较强的关联性。LSTM是一种循环神经网络，通过内部特有的门控状态来记忆长远的历史数据并且捕捉随时间变化的特征信息，因此选择LSTM作为预测模型，接收GAN模型整合出的数据进行预测，其计算过程为

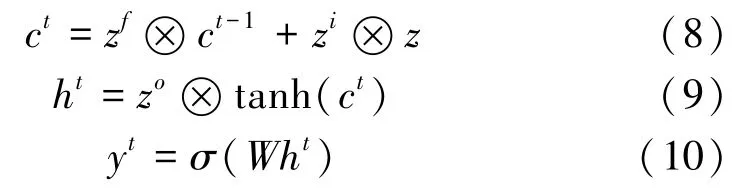
式中:h t为隐藏传递状态；z为当前输入和上一个传递状态h t-1的向量乘积；z f，z i，z o为内部的门控信号；ct为当前时间步的内部细胞状态；y t为当前时间步的输出；W为连接各个门的权重。

3 试验设计及结果分析

设计对比试验，以研究不同模型在数据缺失条件下的预测性能。以清溪水文站的实测水文数据集为例，展示了模型的性能，并与目前几种经典的水文预报方法进行比较。

3.1 数据集

采用清溪河清溪水文站从2003年1月1日到2005年9月26日共计1 000 d的观测数据作为试验数据。由于设备损毁、人为失误等因素造成了部分数据缺失，因此1 000 d里实际观测记录数据的只有882 d，缺失了118 d的数据。

水文站的监测信息纷繁众多，包括水位、流量、流速、含沙量、降雨量、蒸发量、流向、水质等。众多相关性不强的外部特征会影响模型收敛速度，为了解决预测模型收敛速度慢的问题，用极端梯度提升法［20］提取最为重要的3个特征并将其作为输入指标。也就是说，每一刻的输入数据由3个变量（流量、降雨量、蒸发量）组成，然后定义水位为预测输出值。

试验中的实测数据集缺失部分主要是输入变量，但难免有输入数据和输出数据均缺失的情况发生。本文所提出的模型是一个插补和预测相结合的耦合模型，其中GAN模型属于插补模型，填充的是输入数据如降雨量、蒸发量、流量。对于输入数据和输出数据同时缺失的情况，仍然利用GAN模型填充输入数据并在相应的输出数据处做一个标记位，最后利用K近邻算法对标记位上的数据进行填充，最大限度地降低这种极端恶劣的数据缺失情况对预测模型的影响。由于本实例应用中数据量相对较少且时间序列预测法适宜于短期预测，因此将对比试验设置成预见期为3 d的短期水文预报。短期水文预报中水文数据的时序性和完整性非常重要，所以各种情况下的缺失数据都应填充后作为模型的训练要素输入模型。

3.2 基准模型

对比试验中采用K近邻算法作为填充数据的基准方法，即把缺失数据邻近点的加权平均值作为估算的填充数据。同时在采用K近邻算法填充数据后的预测模型中使用水文预报中经典的SVR模型和ARIMA模型的组合模型作为GANL模型的试验对比模型，试验环境和参数设置如下。

SVR模型中的内核函数用于更改输入空间的维数，从而产生更为可靠的回归，对模型预测性能的改善起着至关重要的作用。核函数有多种，如线性、多项式、径向基函数、多层感知等，本文选用径向基核函数RBF。同时选用两步网格搜索方法对SVR参数进行了优化，与传统方法（例如反复试验）相比，可以更有效、更系统地校准参数。本文所采用的SVR模型是利用Chang和Lin开发的LIBSVM工具箱建立的。

为了使ARIMA模型适用于水文时间序列数据并进行有效预测，采用模型识别、参数估计和诊断检查3个步骤来建立最优模型。在识别阶段，将经验自相关模式与理论模式进行匹配，使用自相关函数（ACF）和部分自相关函数（PACF）来确定最佳拟合模型参数（p，d，q），其中:p表示模型中滞后观测值的数量，d表示原始观测值相差的次数，q表示移动平均窗口的大小。通过观察序列的自相关函数和偏相关函数图，初步确定模型参数:p=0～5，d=0～2，q=0～2。一旦确定了暂定模型，就可以直接估算模型参数，使误差最小化。参数估计可以使用非线性优化程序来完成。模型构建的最后一步是对模型进行适当的诊断检查。如果模型不够好，则应确定一个新的暂定模型，然后再次进行参数估计和模型验证。通过多轮对比试验，本文选择了参数为（5，1，0）的ARIMA模型。

3.3 评价指标

由于填充数据的质量高低不能直观展示，因此各模型性能均通过整合后数据的最终预测结果表现来体现。为了从多角度衡量模型的预测效果，本文采用平均绝对误差（MAE）、平均绝对百分比误差（MAPE）、均方根误差（RMSE）作为预测准确性的度量指标，公式如下:

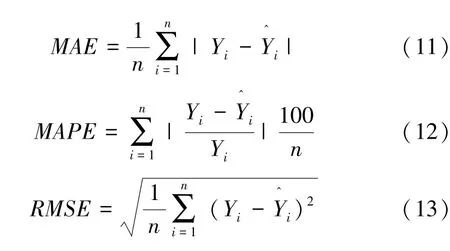
式中:Yi为实测值为预测值。

3.4 试验结果分析

为了验证本文所提出的模型在缺失数据条件下的预测性能，分别与采用了K近邻算法填充数据后的SVR模型和ARIMA模型进行了预见期为3 d的水文预报对比试验。试验将填充整合后前800 d数据作为训练集，后200 d数据作为测试集，结果如图3所示。

图3 填充数据后各模型预测结果比较

与此同时，设置完全相同的试验环境和参数直接对原始实测数据在各模型下进行水文预报对比试验，结果如图4所示。

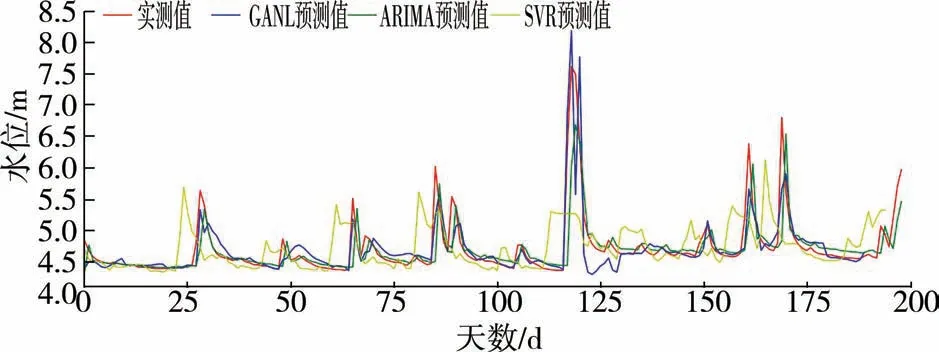
图4 实测数据下各模型预测结果比较

对比图3、图4发现，填充后的数据拟合结果显著优于有缺失的实测数据拟合结果。

图3 中各个模型预测值在训练集和测试集中的平均绝对误差（MAE）、平均绝对百分比误差（MAPE）和均方根误差（RMSE）分别见表1和表2。

表1 训练集模型性能对比

表2 测试集模型性能对比

从表1、表2可以直观地看出，本文所提出的模型在缺失数据条件下的预测性能强于另外两个模型。图3展示了各个模型的预测结果和实测值的拟合情况，其中SVR模型的预测效果最糟糕，这是因为SVR模型在数据缺失条件下的鲁棒性很差，无法挖掘缺失数据的隐藏信息甚至可能在填充数据后引入了缺失值和预测值间本来不存在的关系，导致模型性能急剧下降；ARIMA模型预测拟合结果整体较好，鲁棒性强于SVR模型，但是仔细观察可以发现模型在部分峰值处预测效果较差，这是因为ARIMA模型对缺失数据采用K近邻算法进行填充，是一种简单的线性平滑处理，如果碰到本身就是峰值数据且出现缺失这种情况的话，就无法有效利用邻近数据挖掘缺失信息，存在估计偏差的问题，预测性能就会受到影响；GANL模型的预测结果最好，这是因为它可以在对抗中学习数据分布并生成高质量的填充数据，不再受到数据缺失的限制，最大限度减弱填充数据时多变量间估计偏差的影响。

4 结 论

通过生成对抗网络在存在缺失的数据集上挖掘数据缺失信息、填充高质量的数据，可以缓解当前水文预报中常见的数据缺失问题。将插补模型GAN和预测模型LSTM进行深度结合，提出的GANL模型，能够在数据缺失条件下实现可靠有效的预测。以清溪河清溪水文站的实测水文数据为例，对GANL模型进行了试验评估，结果表明，在数据缺失条件下其性能显著优于其他模型。