考虑调峰经济收益的多目标储能调峰优化策略

靳一奇

（上海电力大学电子与信息工程学院 上海市 200090）

储能技术发展至今，虽然国家能源局获批的储能示范项目数量逐年递增，但是仍然处于试验阶段，想要储能技术市场化还需要很长的路要走[1]。针对储能技术应用于各种场景下，建立合适的计及经济性的储能调峰模型是使其充分实现经济效益最优和新能源发电利用率最大化的必要手段。储能系统应用主体的场合不同，产生的效益不同，起到的作用也不同。归纳分类为：可再生能源发电测、电网测和用户侧[2]。Oudalov 等人在文献[3]中研究了一个瑞士工业用户的真实案例，经过理论分析，建立的储能调峰系统似乎可以在20年中获利近32000 欧元。但是由于无法避免负荷预测过程中出现峰谷偏移，因而实际配置的储能系统容量会比预计的要大，相应的储能系统成本会增加，储能系统的获利空间会被大幅压缩。在文献[4]中，通过实际数据进行了分析计算，每千瓦装机容量的储能系统每年预计可以得到140 美元左右的收益，但是法国的实际峰谷电价差没有计划中的3 倍那么大，因此获利空间也相对减少。但是世界范围内储能系统示范工程还是在广泛地应用中取得长足的进步，其中也不乏许多项目获得了良好的效果。

针对效益评价的研究在前述的储能系统应用电网侧带来的效益基础上，考虑国家的电价政策，通过低储高发的手段实现套利。文献[5]开发了集中运行的隔离系统经济运行优化模型，评估了储能系统调峰的经济效益和调峰效果。文献[6]构建以系统收益最大化为目标的储能调峰优化模型，综合考虑钒电池储能系统三方面效益。文献[7]建立了系统投资成本最小和净收益值最大的多目标优化模型，选取智能算法中的遗传算法对该模型求解。文献[8]提出了一种兼顾混合储能系统经济效益和功率优化分配的双层优化模型，该文章提出的模型对多储能系统协调合作运行模式的应用和市场推广起到了理论指导作用。文献[9]选用动态规划法对建立的优化模型求解，该模型将延缓电网投资升级产生的效益最大化作为目标函数，加以相关约束条件，最终确定最佳容量配置规模和符合经济要求的单位造价。文献[10]提出一种储能系统辅助火电机组进行深度调峰的分层优化模型，该模型上层和下层均采用改进粒子群算法进行计算，中层模型则选用迭代的方法求解。文献[11]从储能系统带来的电量效益、环境效益、经济效益和运行效益出发，建立了以经济行为目标的储能装置参与电网削峰填谷优化模型，使储能系统容量配置最优，完成经济性使用效果。文献[12]建立的数学模型是将经济性作为主要目标函数的储能容量优化模型，其评价体系是站在投资收益和社会效益的角度上制定研究的。

1 计及经济性的储能调峰优化策略

1.1 目标函数

本文选取风力发电并网，主要原因是风力发电目前是新能源发电中随机不确定性较大的一种且较为普遍，电力系统运行要求安全平稳，故系统的负荷曲线就要相对平缓，同时调峰任务的完成也会带来相应的收益，所以构建的目标函数包括两个方面，即以负荷方差最优和经济收益最大。

最小负荷方差如下式：

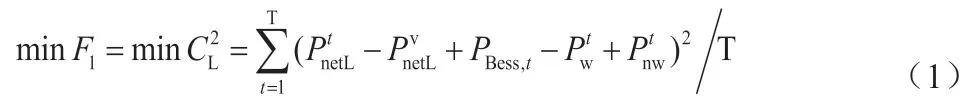
式中PtnetL为t 时段实际电网负荷；PventL为实际电网负荷平均值；为t 时段风电上网功率，取值范围为t时段弃风功率；PBess,t为t 时段储能系统充放电功率。

储能系统参与电网削峰填谷时由分时电价造成的经济模型如下：

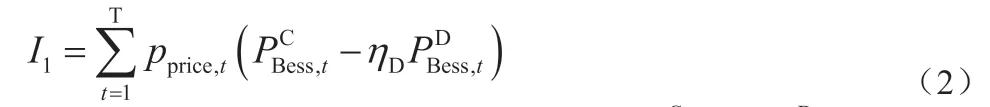
式中pprice,t为t 时段电网峰谷分时电价；PCBESS,t、PDBESS,t分别为t 时段储能系统充放电功率，是储能系统放电效率。则I1可以表示储能调峰时由峰谷电价差带来的利益。

储能系统参与电网削峰填谷时政策激励产生的经济效益模型如下：

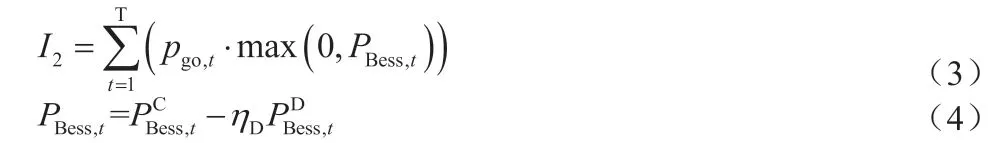
式中pgovernment,t为储能系统调峰时减少单位峰值功率的经济补贴；当储能系统放电移峰时当储能系统充电时即不接受补贴。则I2可表示政府对储能调峰的政策激励效益。

储能调峰经济性优化目标函数：

由于负荷方差最小和经济效益最大评价的内容不同，量纲也不相同，对两个目标函数直接进行加权是不合理的。因此两个目标函数归一化后分别为：

则最终的目标函数为：

1.2 约束条件

为了使优化策略调峰更具优越性，系统约束在一些常规约束基础上增加了可靠性约束，分别如下：

1.2.1 系统功率等式约束

通常认为系统功率平衡约束是系统内包括风电实际上网功率在内的所有机组的出力必须和系统实际负荷加上实际网损相等，但为了简化模型，网损可以忽略不计，因此发电总量等于系统负荷功率加上储能的充放电功率再减去调峰不足量。

表1：储能系统参数

表2：实验结果

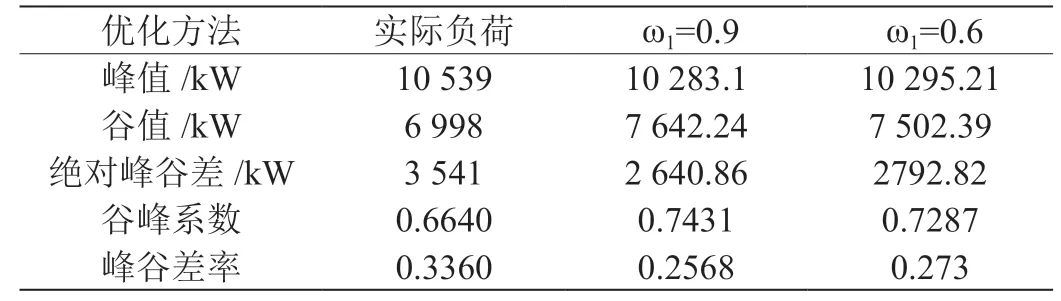
表3：实验结果

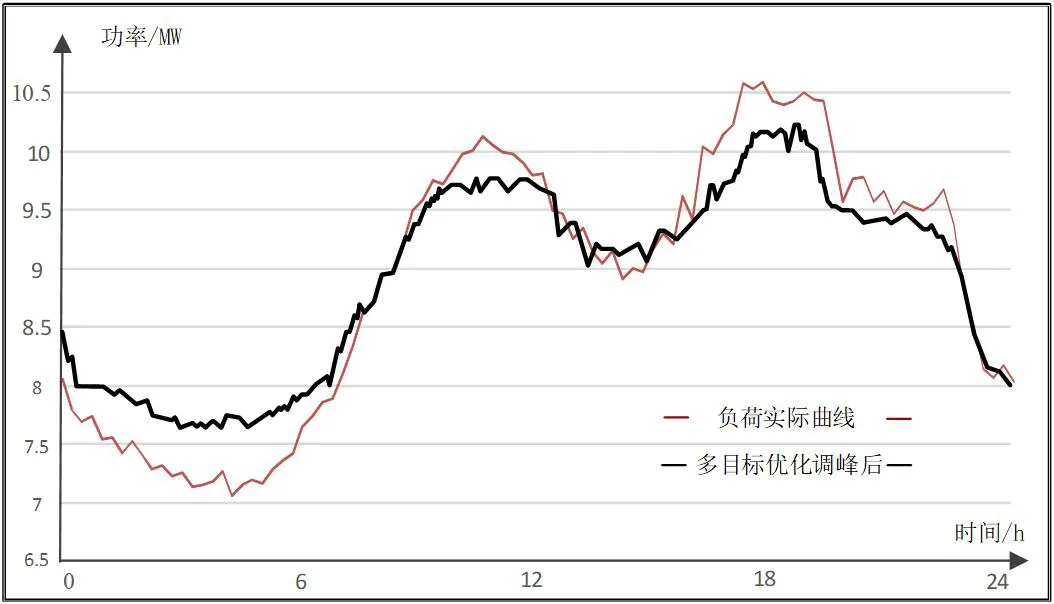
图1：多目标优化模型调峰前后（ω1=0.9，ω2=0.1）

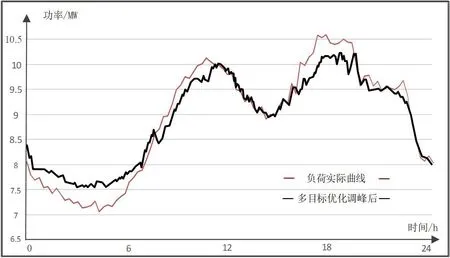
图2：多目标优化模型调峰前后（ω1=0.6，ω2=0.4）

式中PG,t是火电机组t 时段总出力；Pw,t是风电机组t 时段接纳功率；PL,t是系统在t 时段负荷功率；ε1,t为系统在第t 时段出现调峰不足的状态，ε1,t=0 表示调峰充足，ε1,t=1 表示调峰不足；P1,t是第t 时段出现的调峰不足量；

1.2.2 火电机组约束

火电机组约束包括出力上下限约束和爬坡速率约束。机组的出力应大于或等于其出力最小值，小于或等于其出力最大值；爬坡速率约束可分为最大向上和向下爬坡率。

1.2.3 风电场的出力约束

1.2.4 储能系统约束

（1）储能系统出力上下限约束，保证出力不超过最大功率，且不出现同时充放电；

（2）储能系统荷电状态（state of charge, SOC）约束，通过引入SOC 对储能系统的剩余电量进行判断；

式中Et为储能系统在t 时段储存的电量；C 是储能系统额定容量；SOCmin是储能系统的最小荷电状态；SOCmax是储能系统的最大荷电状态。

1.2.5 弃风约束

目前对于储能调峰优化模型建立中，考虑弃风约束的很少，为提高风电消纳，加入弃风量约束，使每天的弃风量在上下限内；

式中a 和b 为给定的每天弃风量上下限，由经验可得；弃风总量Enw为每一时段弃风功率总和。

1.2.6 可靠性约束

可靠性约束主要考虑在一定时间内调峰不足概率小于某一给定参数，另一可靠性为在一定时间内弃风概率小于某一给定参数。

式中K1是在一定时间内调峰不足概率最大值；Kw是给定的系统在一定时间内弃风概率最大值；式中εw,t为系统在第t 时段出现弃风的状态，εw,t=0 表示不用弃风，εw,t=1 表示弃风；当Ptnw=0，εw,t=0，当Ptnw＞0，εw,t=1。

2 评价指标

为了对建立的储能参与含风电并网的电力系统移峰填谷模型的调峰结果进行优劣比较，从技术角度给出了如下评价指标：

2.1 负荷绝对峰谷差

2.2 谷峰系数

负荷谷风系数α 可以表示负荷曲线的平缓程度，α 值越大则表示负荷曲线波动幅度越小即越平缓。

2.3 负荷峰谷差率

负荷的峰谷差率β 给出定义为在一段调度时间内负荷的峰谷差与负荷最大值之间的比值，其代表了这一段时间内负荷的波动程度，β 值越小波动范围越小。

2.4 弃风总量

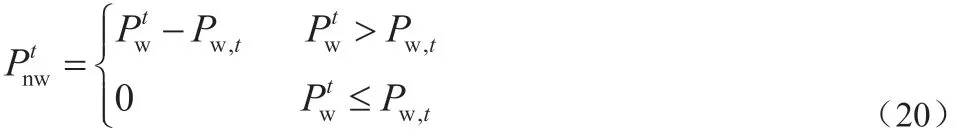
弃风总量如公式（15）中Enw所示，当风电上网功率高于系统可接纳功率时，会出现弃风现象。

3 模型求解方法

根据目标函数和相关约束条件的特点，决定在进行非线性约束方程转化后，采用改进粒子群算法对储能调峰模型求解，得到优化后的储能系统充放电功率。公式（10）中的每个元素是由一个二进制变量乘以一个连续变量得来的，它是非线性的，为求解方便需要将式（10）转换为线性方程。因此引入新的变量：

则式（10）变为：

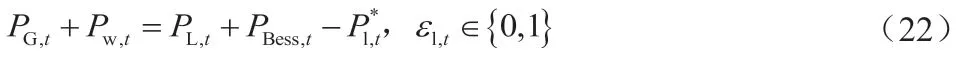
此时线性化式（22）只需单独考虑变量 即可，将式（21）改写成3 个线性不等式约束，即：

4 算例分析

本文选择某市电力公司2016年某日负荷作为实验数据，进行电网调峰仿真。储能系统选用已经大规模投入使用的电池储能系统，其参数如表1 所示。

选择的分时电价参数如表2，政策补贴选择国家规定的中西部地区每千瓦奖励550 元

实验时选择两组不同的权重系数，分别为ω1=0.9，ω2=0.1 和ω1=0.6，ω2=0.4。其中权重系数ω1反映的是该模型中储能调峰效果的重要程度，ω2反映的是该模型中储能调峰经济性的重要程度。当ω1选取的值高时，则该储能调峰模型以优化储能调峰效果为主；当ω1选取的值低时，意味着ω2选值就高，储能系统参与电网移峰填谷的经济性权重相对提高。当优化结果偏向优化经济性目标时，移峰填谷效果指标将变差。但按照普遍情况来看ω1＞0.5，因为储能系统建设的首要目的还是调峰。仿真结果依次如图1、图2 和表3 所示。

由以上选取的不同权重系数的两组仿真结果对比可知，当储能调峰优化模型考虑了经济性因素时，由于想要调峰效果优化和经济性优化达到一种最优平衡，故负荷的调峰优化效果会有一定程度上的下降，且随着储能调峰效果的权重系数ω1减小，移峰填谷效果会随之变差。不过综合所有结果分析，依然能够很好地完成移峰填谷任务，证明储能系统应用电网移峰填谷的经济性与移峰填谷效果可以实现有机统一。

5 总结

本文的主要内容是分析储能系统参与风电并网的电力系统移峰填谷时如何兼顾调峰效果和经济收益，其中经济性因素就包括两部分即分时电价下的低储高发套利以及完成调峰的政策激励，以此为基础建立计及经济性的储能系统参与电网移峰填谷的优化模型，根据建立的目标函数和相关约束条件的特点，决定在进行非线性约束方程转化后，采用改进粒子群算法对储能调峰模型求解，得到优化后的储能系统充放电功率。通过算例分析，目标函数中选取不同的权重系数，对比实验结果。储能系统应用电网峰填谷的经济性与移峰填谷效果可以在某种程度上达到一种平衡，两者并不是绝对的矛盾体，即满足良好的调峰效果情况下兼顾到储能系统调峰的经济效益。