地震条件下抗滑桩有限杆单元时程法与离心机模型试验研究

金亚兵，孙 勇，徐晶鑫

(1.深圳市地质局，广东 深圳 518023；2.贵州大学 喀斯特地质资源与环境教育部重点实验室，贵州 贵阳 550025)

我国位于世界两大地震带之间。2008年，汶川地震由于其震级高，又位于西部山区，大量边坡、滑坡破坏，严重影响救灾工作。抗滑桩作为一种有效加固措施已得到大量应用，然而抗滑桩在地震作用下的研究才刚开始起步，特别是计算理论有必要进行深入研究[1-2]。

地震作用下抗滑桩的研究主要有试验法、数值分析法、拟静力法和时程法。模型试验分为1g(g表示重力加速度)的振动台试验和Ng的离心机试验。

国内一些学者进行了1g的大型振动台试验，对岩质边坡和土质边坡进行地震波作用下边坡滑坡的振动试验。普通1g振动台模型试验规模较大，实施简便，但也存在诸如不能满足关键的相似比尺等缺点。Ng条件下的离心机振动台试验在相似关系方面具有很大的优越性，可以深入了解地震作用下的滑坡及抗滑桩等加固的地震响应和抗震机理，推进对滑坡及其抗震加固的全面认识。刘红帅等[3]对岩土边坡地震稳定性动力试验方法进行了总结，于玉贞等[4]对抗滑桩进行了静力与动力破坏离心模型试验和对比分析，涂杰文[5]对抗滑桩加固滑坡体地震反应进行了离心机模型试验，郑桐等[6-7]对锚拉桩和悬臂桩进行了动力离心机试验。

国外的研究最早在1981年，WHITMAN等[8]进行水平砂土地基动力响应试验。之后，HUSHMAND等[9]研究了一维土层的动力问题，LEE等[10]进行了砂坝和人工砂岛的动力试验，TUFENKJIAN等[11]研究了土钉支护基坑的动力稳定问题，CURRAS等[12]进行了群桩动力试验，DEWOOLKAR[13]用土工动力试验研究了悬臂式挡土墙后饱和可液化无黏性土的动力响应问题，LING等[14]进行了加筋土挡墙的动力试验，KAGAWA等[15]进行了土-桩-结构物相互作用动力试验，LEE[16]对沉箱型码头墙进行了动力试验，BRANDENBERG等[17]对单桩和群桩在可液化均质地基中的动力问题进行了动力试验。

目前采用的数值计算法主要有：有限元法；有限差分法；快速拉格朗日法；边界元法；离散元法；非连续变形分析方法。许江波等[18]采用动力强度折减法，利用无损音频压缩编码(free lossless audio codec，FLAC)软件，提出了新的有限元设计方法。虽然进行数值计算的学者较多，但由于岩土的静力，动力本构模型较难反应岩土的真实情况，所以这方面的研究还有待加强。

关于拟静力法，为了减少计算工作量，早期多采用拟静力法，即将地震动力用静力代替进行计算，是对静力稳定性分析方法的一种延伸。拟静力法已被广泛应用于简单滑坡的动力计算，但其没有考虑地震动的动力性质，如时程特性和频谱特性等。薛守义等[19]对块状岩体边坡地震滑动位移进行了拟静力分析，肖世国等[20]对土坡抗滑桩进行了地震条件下的拟静力分析。

关于时程法，抗滑桩地震作用下的时程法研究文献很少。在抗滑桩静力计算中，应用广泛且比较成熟的方法为弹性地基梁法。本文首次提出了基于弹性地基梁理论的有限杆单元时程法，对地震条件下的抗滑桩进行时程计算分析，并且进行了抗滑桩的离心机模型试验。时程法与试验法对比结果表明，本文提出的计算方法是有效和可行的。

1 地震条件下基于有限杆单元法的时程法

本文提出的抗滑桩计算方法采用了有限杆单元法(矩阵位移法)理论，多质点有阻尼体系动力反应的振型叠加法理论，Reyleigh阻尼理论。桩可以当做直杆单元加以离散化，每个杆单元有2个节点，每个节点有2个未知数，一为挠度位移，另一个为转角。杆单元的多力除滑坡推力、桩前抗力外，还受周围土体的弹性抗力作用。

1.1 基本分析过程

1)对每个单元建立单元刚度矩阵、单元质量矩阵和单元的外向量矩阵。

2)将局部坐标下的单元刚度矩阵转换成整体坐标下的单元刚度矩阵[K]e，单元质量矩阵[M]e，单元外力向量矩阵[P(t)]e。

(1)

3)单元刚度矩阵、单元质量矩阵、单元外力向量矩阵组装形成体系的总刚度矩阵[K]，单元质量矩阵[M]，单元外力向量矩阵[P(t)]。

(2)

4)形成体系的运动方程。

(3)

式中：{u}为结点位移矩阵；[C]为阻尼矩阵。

5)求体系的自振频率。

6)求体系的振型。

7)用振型叠加法求解结构体系的运动方程。

将{u}作正则坐标变换，则

[u]=[φ]{q}

(4)

将式(4)带入运动方程，有

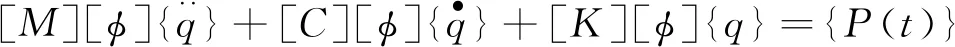
(5)

将式(5)代入运动方程(3)，有

[φ]T[K][φ]{q}=[φ]T{P(t)}

(6)

引入Rayleigh阻尼后，[φ]T[C] [φ]也为对角矩阵，各对角元素为：

(7)

式中：Mn为振型质量；Kn为振型刚度；Pn为振型荷载。

将式(7)带入式(6)，有

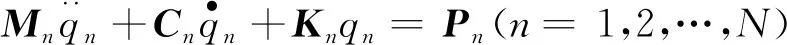
(8)

式(8)为解耦的N个单自由度有阻尼强迫振动方程，可以用Duhamel积分、Fourier变换等方法求解。当用Duhamel积分求解时，计算得

(9)

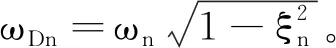
单位脉冲反映函数

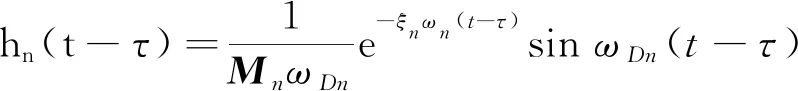
(10)

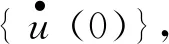
(11)

由非零初始条件产生的自由振动为

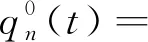
(12)

振动的全解为

(13)

通常选取3～5个振型计算就能满足计算精度的要求。

1.2 单元刚度矩阵的建立

我们推导了桩周有弹性抗力的杆单元刚度矩阵：

(14)

其中：

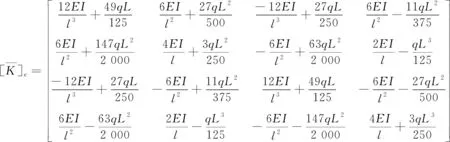
(15)

式中：E为桩的弹性抗弯刚度；l为单元长度；q为桩的水平弹性抗力；L为杆单元长度。

2 计算实例

抗滑桩单元节点划分如图1所示。

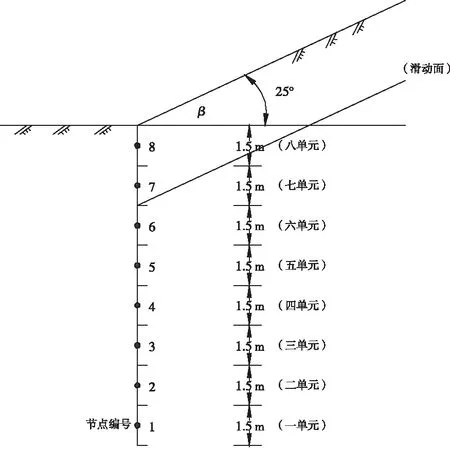
图1 抗滑桩单元节点编号

2.1 滑坡推力计算

滑动面用软黏土制备，用三轴试验测得黏聚力c=5 kPa，φ=7°，砂土φ=35°。

滑坡下滑力(滑坡推力)计算，桩间距为4 m，滑坡体厚为3 m，滑体长为24.38 m，则下滑力其在水平方向的分力为878.76 kN(试样桩前被动土压力抗力之后的值)。下滑力按三角形分布，分配到节点上的荷载如图2所示。

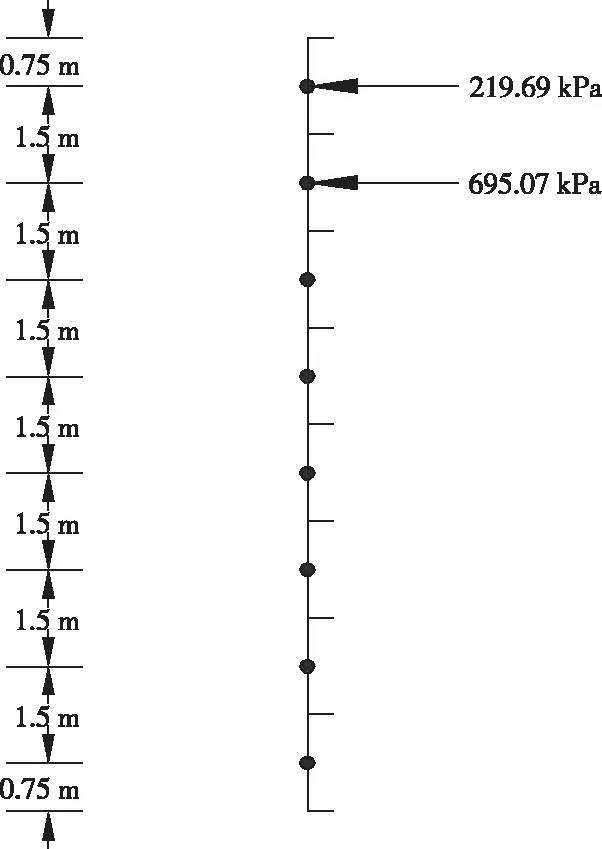
图2 抗滑桩上作用的荷载

2.2 基于土压力与位移关系式的地基系数

目前各规范对地基系数都是按土名查表得到，本文则采用梅国雄提出的土压力与位移的关系式，通过求导得到地基系数。关于土压力与位移的关系式，梅国雄，欧明喜等[21-22]等学者对此问题进行了研究。这种方法比规范查表法更合理。

梅国雄的土压力与位移的关系式中的土压力是采用的静力条件下的值，为此孙勇，徐利敏等[23-25]推导了地震条件下土压力值公式。国外学者从上世纪30年代开始就对支挡结构的土压力进行了试验研究。TERZAGHI[26-28]对干砂进行了大型模型试验，SHERIF等[29]对挡墙的静止土压力和主动土压力进行了模型试验，FANG等[30]对各种位移的土压力进行了模型试验，CHANG等[31]对黏土的土压力进行了模型试验。国内学者从50年代开始也进行了大量的支挡结构土压力试验，应宏伟等[32]对基坑挡墙的土压力进行了研究。

主动土压力、静止土压力、被动土压力与位移的关系如图3所示。

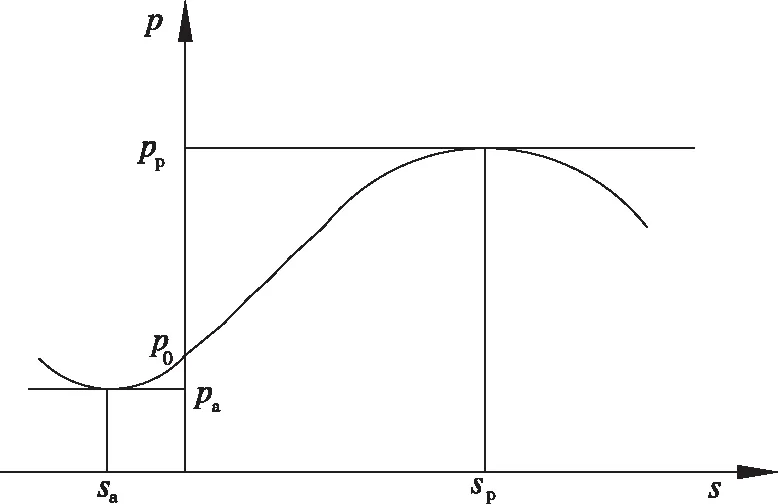
图3 主动土压力、静止土压力、被动土压力与位移的关系

梅国雄建立了考虑位移的土压力-位移模型为

(16)

式中：k(h)为内摩擦角的函数；b(sa,h)为主动土压力位移量和内摩擦角的函数，且有b>0；p0为静止土压力的一半。

对式(16)求导，得到地基系数的比例系数：

(17)

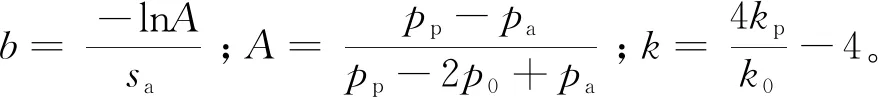
式中：p0为静止土压力；pa为主动土压力；pp为被动土压力；k0为静止土压力系数；kp为被动土压力系数；s为位移，一般取10 mm；sa为主动土压力的位移，一般取0.002H(H为桩深度)。

计算得到各单元中点处的地基系数的比例系数，见表1。

表1 地基系数的比例系数计算值 单位：kN/m4

取平均值，则m=5 004 kN/m4。

2.3 桩顶位移计算

计算得到的桩顶位移如图4所示。从图4可见，桩顶最大位移约在11 s出现，最大位移为4.66 cm。

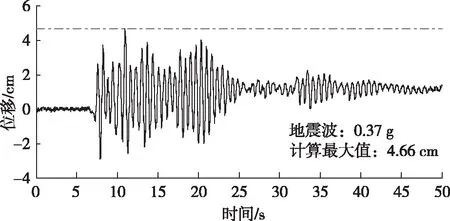
图4 桩顶位移计算图

2.4 桩身弯矩计算

计算桩身分别为3、4.5、6、7.5、9、10.5 m处的弯矩，如图5所示。由图5可以看出，最大弯矩为1 380 kN·m，位置在离桩底4.5 m处。

图5 桩身弯矩计算图

3 离心机模型试验

离心机试验在浙大ZJU400g-t离心机上进行，地震输入为EL-Centro地震曲线，最大加速度为0.37 g。离心机如图6所示。

图6 ZJU400g-t土工离心机

离心机模型试验在模型箱中安设了加速度计，桩顶测位移的位移计，桩身测弯矩的应变计。实际工程桩截面为1.25 m×1.25 m，模型桩几何尺寸按相似比尺N=50缩制，即模型桩截面尺寸为25 mm×25 mm，桩间距取80 mm。通过计算，结合试验工况，需抗滑桩数目为5根。试验简图如图7所示。

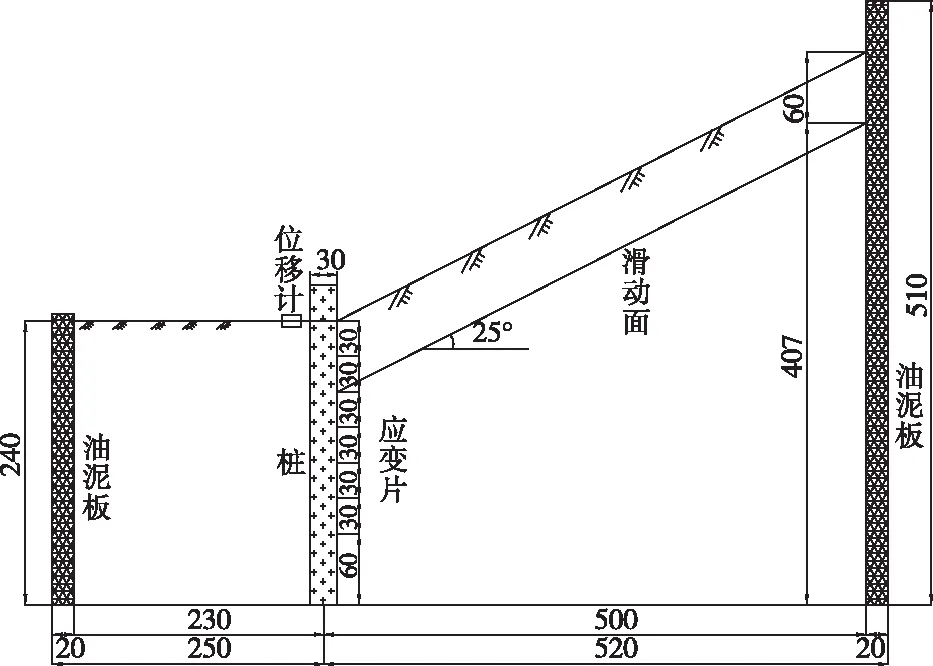
图7 离心机模型试验图

3.1 桩顶位移测试

图8为桩顶3个位移传感器在El-Centro地震波作用下的桩顶位移图。由图8可以看出，桩顶位移最大值分别为4.56、4.61、4.62 cm。

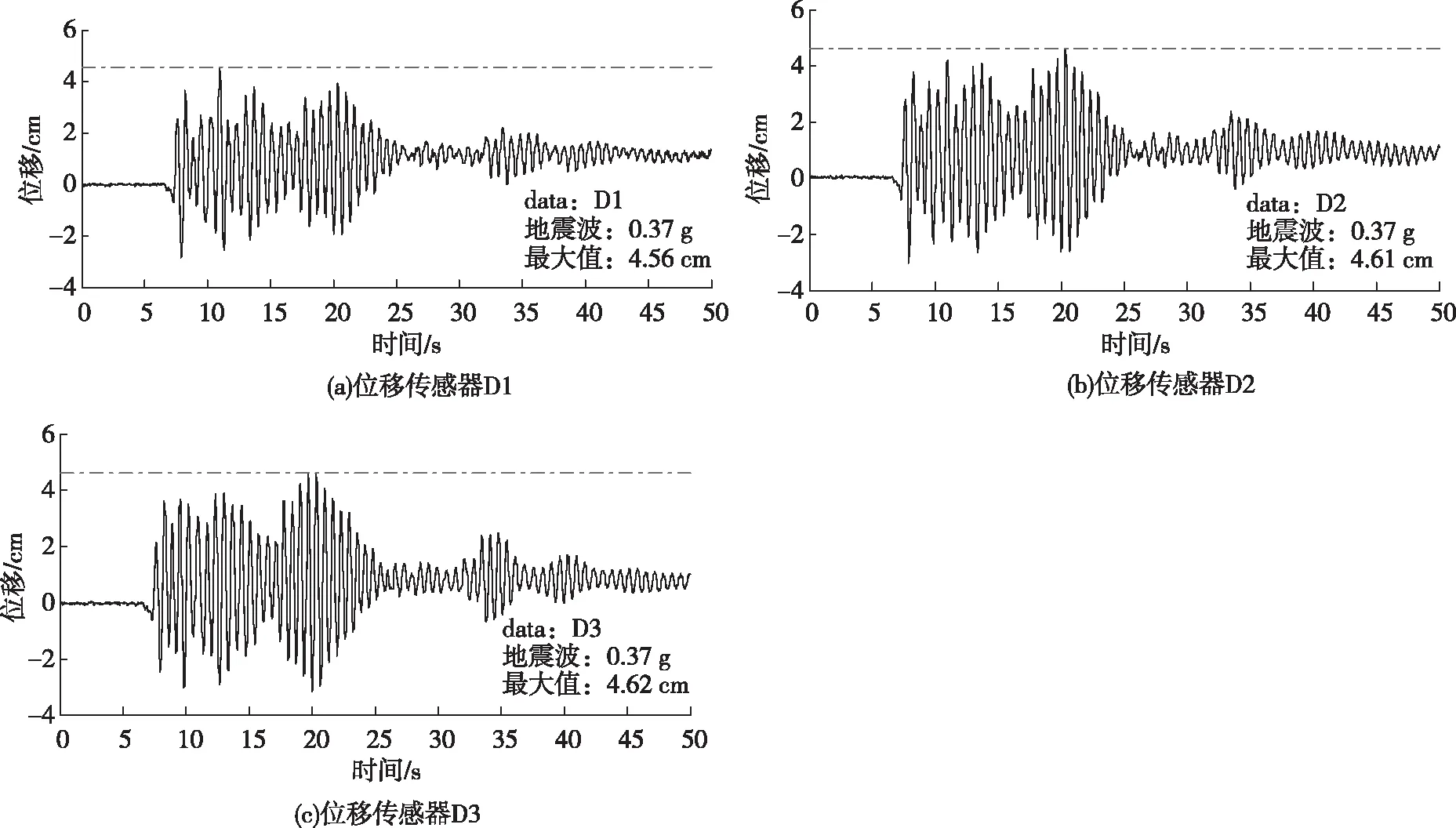
图8 输入0.37 g时桩顶位移曲线

3.2 桩身弯矩测试

图9为El-Centro地震波作用下的桩身弯矩测试曲线。由图9可以看出：最大测试弯矩为1 315 kN·m，位于桩身4.5 m处。

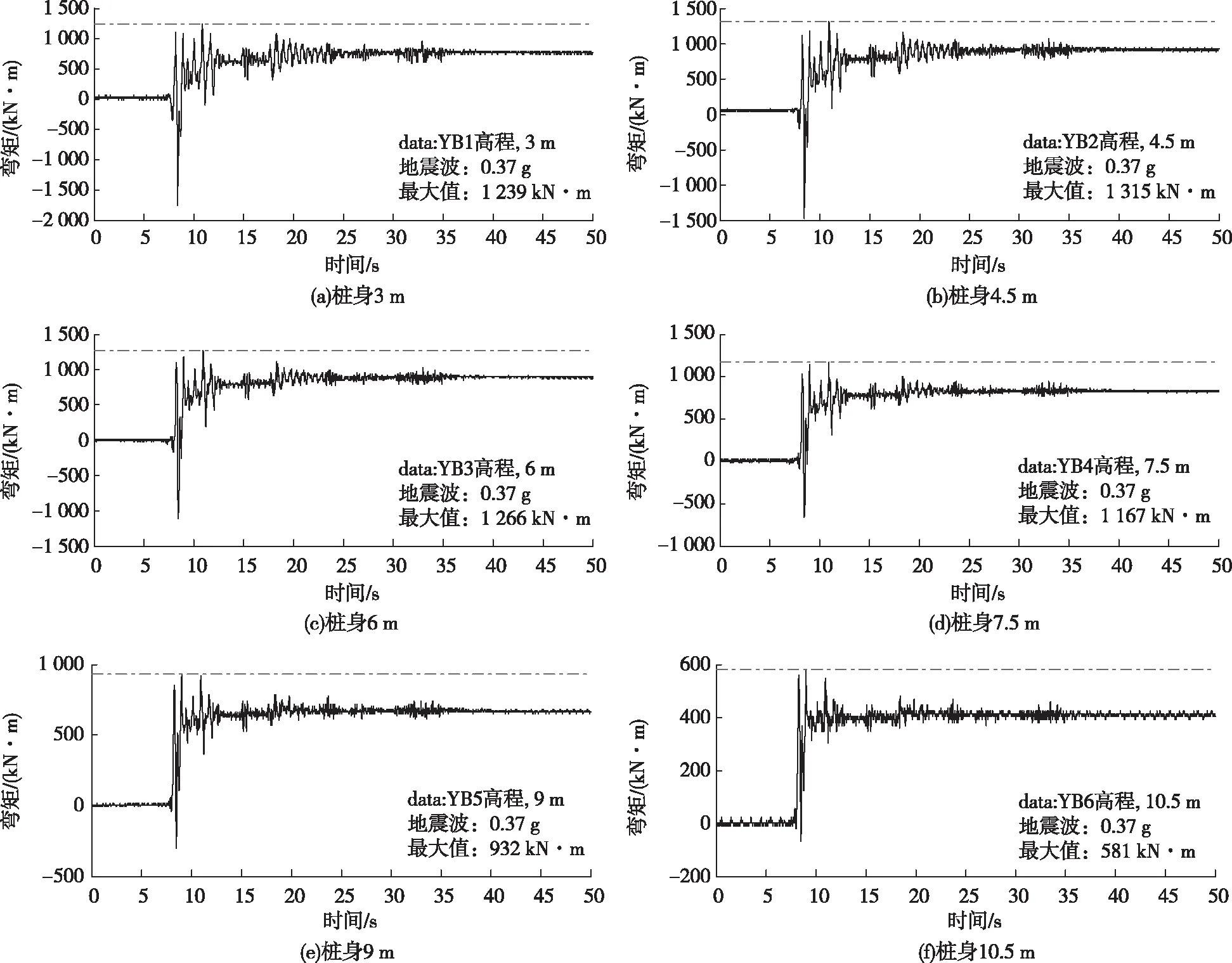
图9 输入0.37 g时桩身弯矩时程测试曲线

4 计算值与实测值的比较

4.1 桩顶位移计算值与实测值的比较

桩1、桩2、桩3桩顶的最大位移见表2。各桩顶的实测最大位移值基本相同，与计算值的误差在5%误差范围内。

表2 桩顶位移计算值与实测值的比较 单位：cm

4.2 桩身弯矩计算值与实测值的比较

桩身弯矩计算值与实测值的比较见表3。由表3可以看出：计算值与实测值相吻合，两者误差在5%内；最大计算值与实测值同时位于离桩底4.5 m处。

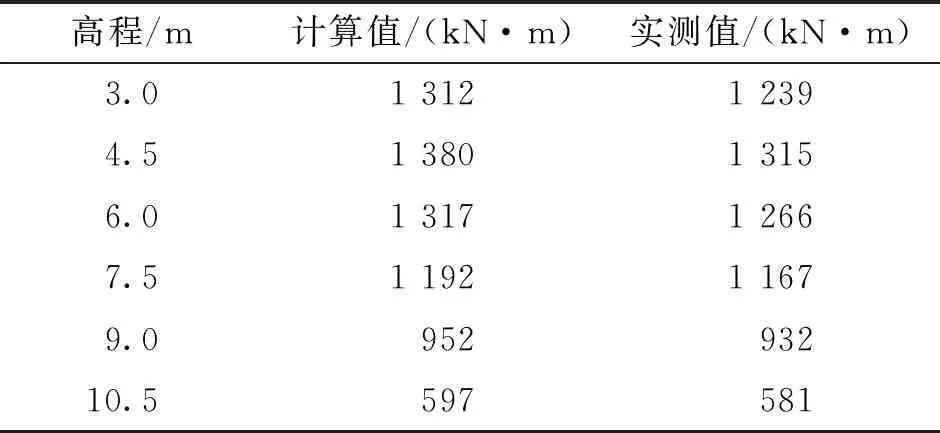
表3 桩身弯矩计算值与实测值的比较

5 结论

1)本文提出的抗滑桩时程计算方法，基于弹性地基梁理论、有限杆单元法理论、多质点有阻尼体系动力反应的振动叠加法理论、Rayleigh阻尼理论，继承了目前规范中广泛应用的静力弹性地基法的优点，并考虑地震作用。

2)本文方法计算的桩顶位移和桩身弯矩与试验得到的值有很好的吻合，误差均在5%以内。

3)本文引入了梅国雄的土压力与位移的关系式，通过求导得到了地基系数的比例参数，比按岩土名查表得到地基系数的比例系数要科学。查表给出的是一个很大范围的值。

4)在浙江大学 ZJU400g-t土工振动离心机上进行了模型试验，试验值与计算值比较相吻合，说明本文提出的新方法的正确性。