关于概率统计教学中“概率定义”教学案例的探讨与思考

何建营 周瑞芳

摘要：概率论与数理统计是理工科类专业必修科目之一。概率的定义是系统化知识体系——概率统计的基石，学习者对此概念的理解程度，决定了他以后在应用时的高度。同时，也会对数学其他概念理解和深入学习产生促进作用。本篇主要讨论概率论中关于“概率”概念统计定义的教学。通过实例与数学软件模拟结合，画图对比演示概率的统计学概念的本质含义，深入浅出地剖析概念中的问题、难点及解决办法。

关键词：概率论，统计学定义，极限，依概率收敛

引言

《概率论与数理统计》是大学理工类专业必修基础课之一，在后期的专业学习、研究生课程学习及专业领域等研究中，有着广泛的应用，它的理论与方法在诸如物理、化学、工程、生物、管理等众多传统学科中发挥着重要作用，同时又在一些新兴学科有着重要作用，如信息论、控制论、可靠性理论、人工智能、大数据、物联网等。概率论与数理统计是目前最为活跃的数学学科之一，在理论与实践教学中，也有着更丰富的素材和背景，是学生们较为感兴趣的一门数学课程。

现状：

概率论与数理统计毕竟是一门严谨的学科，有着数学学科的抽象性与严谨性，但同时，也有着自身的特点。概率论最大的特点就是研究对象的不确定性，是对事件发生的可能性的讨论，从某种意义上说，是一对多的关系的研究，这一点上，与高中学习的函数这一概念有所区别，是数学中与映射关系对应的另一种数学关系。虽然高中学生们已经接触过概率统计相关知识，鉴于高等数学的研究手段，大学阶段，需要同学们先行修读高等数学或数学分析的相关基础课程，满足学习的必备知识。

不过在学习了高等数学课程以后，同学们在进行概率课学习的过程中，对有些概念的理解容易混淆，或者是理解的似是而非。在概率统计这门课中，包含了很多同时也很抽象的知识点和定理。例如概率的公理化定义，依概率收敛，测度，中心极限定理，假设检验等等，这些概念以及定理在概率论学习中不容易理解，更加不容易理解精确和深刻。有些定义如随机变量，多维随机变量，随机变量的分布和条件分布，数字特征，中心矩，原点矩等等，学生虽然能够记住，但是掌握得并不好，在后期的应用上更加满足不了所需所学。以至于在有些研究的后期阶段用到概率有关知识时，经常闹出笑话或者犯严重的概念错误。

大学数学课程培养学生的目标就有培养学生抽象思维能力，能够举一反三，真正学以致用。高等数学培养了学生从有些到无限的思维模式，培养了划分、近似替代、求和、无限逼近极限的思维;那么概率论与数理统计培养的就是学生从确定性到随机性不确定性转变的思想。但是这种思维转变需要由形象具体到抽象有一个过程转变，需要对学生加以引导。

下面就概率统计教学中的案例给出探讨，从而达到学生学习该定义理解的深入：

修读或者講授过高等数学的人都十分清楚极限的定义，一种是对极限的描述性定义，

从上图中，容易发现，在从某有限项开始以后，数列的值开始趋于稳定，也就是说，摆动地或者超出某个范围的可能为零，换句话说，都落在了某个稳定值的附近。

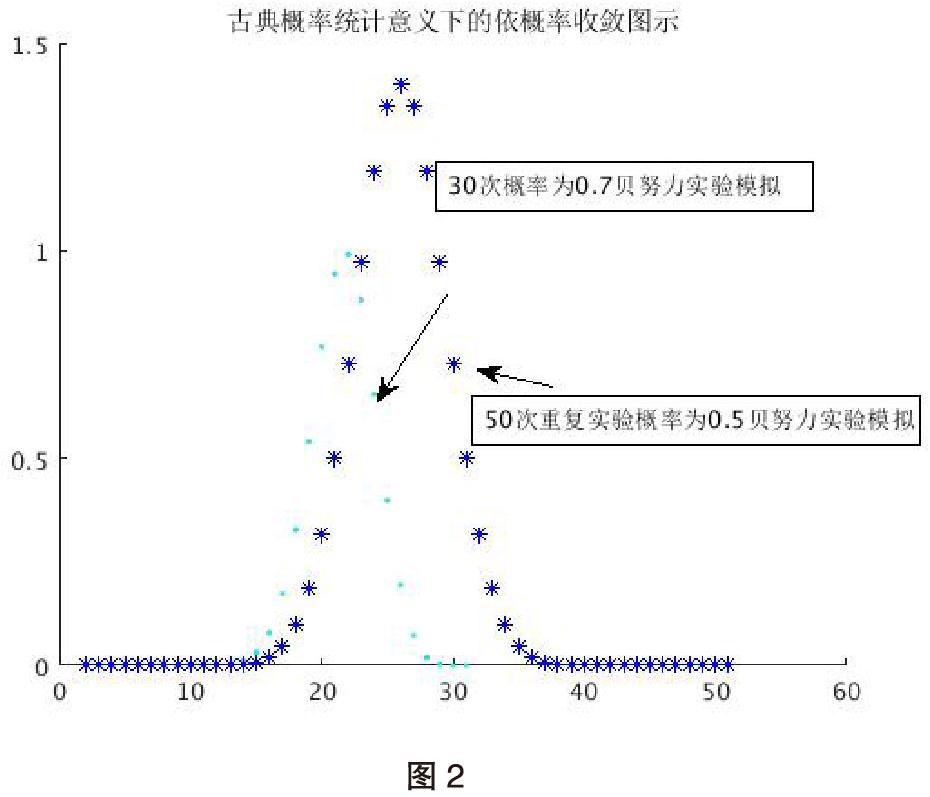
对于概率的统计定义，很多同学就会想当然认为，概率不就是频率的极限吗？当，认为频率。我们细想，真的是这样的吗？这其中是有着本质区别的。区别就是，频率并非收严格收敛与，而是依概率收敛与。这里边其实是有着区别的，但是在介绍依概率收敛的定义之前，同学们首先学习的是概率的统计定义，接着是公理化定义。于是乎，就想当然地认为，频率的极限就是概率了。诚然，大数定律告诉我们这样一个事实：随着实验次数的增加，频率会越来越稳定接近于某个常数。这一陈述没有问题，问题出在了“越来越”三个字上，这一模糊的描述其实就蕴含了依概率收敛的意思，我们一抛硬币实验为例：显然这是一个n重贝努力实验类型，服从二项分布，随着实验次数的增加，最终我们发现，出现正面向上的频率多数是接近1/2的，但我们就能说极限是1/2吗？错！显然，我们实验的次数对于极限无穷来说，还差很远，事实上，完全有这种可能，实验了很多次，恰好都是出现反面向上，或者只仅仅出现了1次，2次…这种可能虽然很低，但我们不能就此说没有可能，只能说可能性几乎为0，（彩票特等奖中奖率不就如此吗）所以说，这里得从统计学出发的概率定义，并没有用极限，实际上，是一种依概率收敛的定义。我们通过计算机多次模拟作图证明，概率的定义与极限定义的不同之处：

从中可以发现，概率的收敛是有别于数列收敛的。所有说，概率并不能简单的以频率极限来定义。

当然，我们也能从中找到解释这一现象的原因：理论上讲，对应抛硬币实验，随着实验次数的增多，应该说出现正面向上的次数与总的次数之比，即频率，应该接近0.5，关于这一点，大数定律可以保证。但是这是接近，只是说在多次重复过程中的统计结果的平均值，而不是多有的值。我们试想一下，完全存在不管做了多少次重复实验，一直都是“正面”超上的结果，虽然说这种可能微乎其微，但不能据此否定这种可能性，或者出现1次，2次，3次……总之比较少的有限次数，只要不是接近一半的次数，这些都是有可能的，这跟买彩票中一等奖的情况很相似，可能性都很小，几乎为零，但却是存在的。以生活中的问题为例，例如小明同学想购买一种彩票，假如说中“头奖”的可能性为10-10，虽然很低，几乎可以认为是零。但是，我们不能就此说他一定不会中“头奖”。因为有可能在他买第一次时，就可能中奖。这种可能性的度量方式，其实就是基于概率的统计学定义给出的。

那么问题出来了，既然概率不是频率的极限，该如何定义概率呢？很多教材这样给出了概率的文字描述定义，说随着实验次数的增加，频率会越来越稳定与某一稳定的数，这一数值，即为对应的事情发生的概率（严格讲是统计学意义下的概率）。这一描述，很相似于高数中数列极限的描述性定义，但有区别，我们仔细对比一下：高等数学数列极限定义会讲，从某项开始以后，“所有的”数列的项会越来越接近某一数。而概率论呢，却从不会说从某项以后开始，而是说越来越接近。也就是说不是所有的，那么显然就有可能有溢出来的一部分情况了，只是说这种可能性较小罢了。

定义 在相同的条件下，进行了n 次试验， 在这 n 次试验中，事件 A 发生的次数 称为事件 A 发生的频数。 比值 称为事件A 发生的频率，并记成 。

显然，频率具有以下性质：

概率的统计定义：在相同条件下重复进行n次试验，当试验次数n充分大时，事件发生的频率稳于某个常数附近，我们称为事件发生的概率。

显然，由频率得到概率统计定义是有缺陷的，统计学概率取值依赖于具体实验，我们不可能对每个事件都做大量的试验，从而得到频率的稳定值。用这种定义很难计算事件的概率。

由于理论研究的需要，受频率性质的启发，于是1933年苏联数学家Kolmogrov提出了概率的公理化結 构，给出了概率的严格定义

概率的公理化定义：设E为随机试验，为其样本空间，对于E的任一个 事件，都有一实数与之对应，称为事件A的概率，如果集函数满足：（1）非负性：对任意事件A，P（A）≥0;（2）规范性：P（Ω）=1;（3）可列可加性：设A1 ，A2 ， ……是两个互不相容的事件，则有：

显然这一概念更加抽象和科学严谨。借助于实验次数的局限，在有限次的样本空间下，规定了等可能性的古典概型的频率统计，也就基本等同于我们平时说的统计学概率了。即

下面就此我们给出一个例子：

例：某接待站在某一周曾接待过 12次来访，已知所有这 12次接待都是在周一和周三进行的。问是否可以推断接待时间是有规定的？

假设接待站的接待时间没有规定，个来访者在一周的任一天中去接待是等可能的，那么一周内接待12次的来访共有712种。而12次接待来访者都在周一，周三的概率为：=212/712=0.0000003

人们在长期的实践中总结得到“概率很小的事件在一次实验中几乎是不发生的”（称之为实际推断原理）。现在概率很小的事件在一次实验中竟然发生了，从而推断接待站不是每天都接待来访者，即认为其接待时间是有规定的。

总结：概率论与数理统计的许多概念比较抽象。由于研究的随机现象具有不确定，与学生之前学习的研究确定性现象的学科如几何、代数、微积分等有极大的不同，在教、学过程中给学习者和讲授者都带来很大难度。应该本着仔细斟酌和联系实践的科学精神，认真领会该学科的奥妙，不足之处敬请指正。

中原工学院 理学院 何建营 周瑞芳