无粘结预应力筋极限应力增量计算方法的对比研究

赵少伟 陈冰 郭蓉 刘真琛

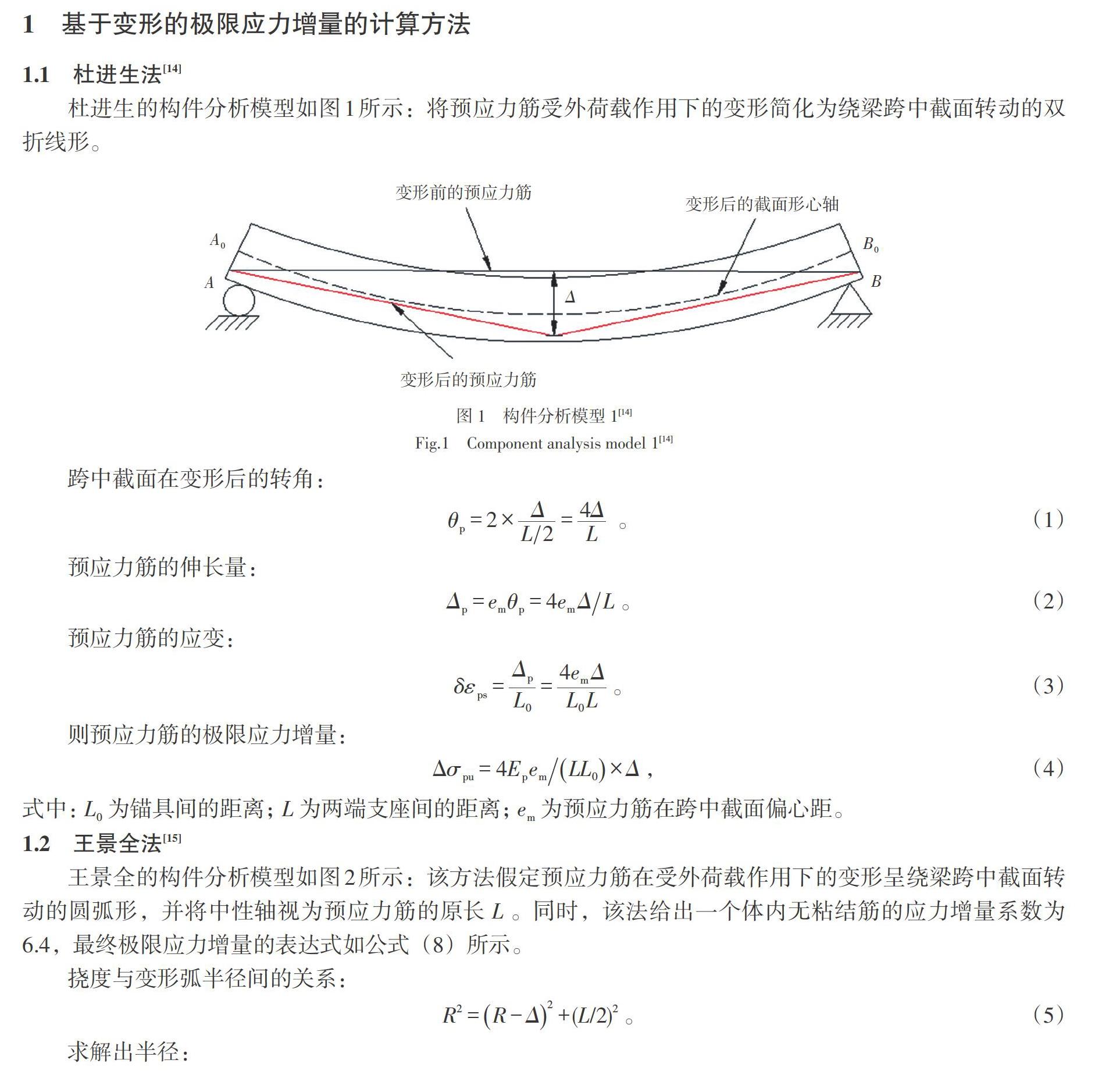
摘要 目前有关无粘结预应力筋极限应力增量的诸多计算方法存在计算复杂或精度较差的问题，基于整体变形的无粘结预应力筋极限应力增量的计算方法有效地解决了这一难题。通过8根无粘结预应力混凝土梁抗弯试验对各国规范中关于无粘结预应力筋极限应力增量的计算方法及现有的基于变形的计算方法进行了对比分析，结果表明：相对于其他计算方法，基于整体变形的无粘结预应力筋极限应力增量的计算方法具备计算简单，结果准确的优点。

关 键 词 无粘结预应力筋;极限应力增量;跨中挠度;结构整体变形;对比分析

中图分类号 TU378.2     文献标志码 A

Abstract At present， many methods for calculating the ultimate stress increment of unbonded prestressed tendons have the problems of too complicated calculation or poor accuracy. The method of calculating the ultimate stress increment of unbonded prestressed reinforcement based on the whole deformation effectively solves the problem. A comparative analysis is made between the calculation methods in the national codes of ultimate stress increment of unbonded prestressed tendons and the calculation methods based on overall structure deformation through 8 unbonded prestressed concrete beam bending test. The results show that compared with other calculation methods， the calculation method based on the overall structure deformation has the advantages of simple calculation and accurate results.

Key words unbonded prestressed tendons; ultimate stress increment; mid-span deflection; overall deformation of structure; comparative analysis

0 引言

無粘结预应力混凝土结构是指预应力筋只通过锚具和转向块向混凝土施加预应力的结构体系，具有承载力高、抗开裂性能强、施工便捷等优点[1]。对于无粘结预应力筋而言，由于没有粘结力的作用，在构件的受力过程中预应力钢筋与混凝土变形并不协调，不满足平截面假定，不能根据各部分材料变形协调获得预应力筋的应力，因此求解无粘结预应力筋极限应力增量是研究该类构件力学性能的难点及关键所在。

目前，各国制定的规范[2-8]都对无粘结预应力筋极限应力增量的计算给出了建议公式。学术界关于此类问题的研究比较丰富，给出的计算方法的种类也比较多，概括起来可以分为以下四类：粘结折减系数法[9-10]、考虑截面配筋指标和高跨比影响建立的回归公式[6]、基于等效塑性铰区长度的计算方法[11-13]、基于变形的计算方法[14-16]。

粘结折减系数法[9-10]是将位于最大弯矩截面无粘结筋处的混凝土应变与一个折减系数相乘，从而得到无粘结筋的应变，其实质是通过此折减系数使无粘结筋的变形仍然服从平截面假定，美国规范AASHTO 1994[4]曾采用此方法计算极限应力增量，然而该方法较为依赖经验，无法给出一个准确的折减系数，因此结果准确度较差，在最新的美国规范AASHTO 2017[5]中已不再使用此方法;根据截面配筋指标建立的计算方法[6]是基于试验研究，考虑了截面配筋率和高跨比影响而建立的回归公式，目前中国规范JGJ92—2016[3]和美国规范ACI318-11[6]均采用此方法进行计算，由于该公式考虑的参数较少且忽略了外荷载及非预应力筋的影响，因此所得结果与实际值相差较大;基于等效塑性铰区长度的计算方法[11-13]是将无粘结筋处的应变集中到塑性铰区，并假设受压区极限应变一定，累积出基于平截面假定的无粘结筋处应变，虽然该方法精度较高，但是理论复杂计算难度大，不适合于工程应用;基于变形的计算方法[14-16]是先假定结构的变形，然后通过几何关系推导出整体变形与无粘结筋处混凝土应变的关系，进而得出无粘结筋极限应力增量的方法。

在以上4种方法中，基于变形的计算方法较为简便，通常只需确定混凝土梁的跨中挠度即可求解出无粘结筋的极限应力增量，因此引起研究者的广泛关注。对于梁的跨中挠度这一重要参数，本文通过无粘结预应力混凝土梁抗弯试验来对比3种经典挠度计算方法，挑选出最接近实测挠度值的计算方法;进而通过试验结果证明无粘结筋极限应力增量与跨中挠度之间的相关关系;最后通过对各国规范中极限应力增量的计算方法[2-8]和基于变形的计算方法[14-16]进行对比分析，验证基于变形的无粘结筋极限应力增量计算公式的正确性。

1 基于变形的极限应力增量的计算方法

1.1 杜进生法[14]

杜进生的构件分析模型如图1所示：将预应力筋受外荷载作用下的变形简化为绕梁跨中截面转动的双折线形。

为考察上述3种刚度计算方法在无粘结预应力构件使用的适用性，本文进行了相关试验研究。

3 试验分析

3.1 试验方案

试验梁均为简支梁，预应力筋布筋形式均为直线型，其中S-1～S-4截面尺寸为[b×h=][300 mm×][400 mm]，全长4.5 m，计算跨度4.2 m;L-1～L-4截面尺寸为[b×h=400 mm×500 mm]，全长5.1 m，计算跨度4.8 m。试验梁预应力筋均为[?s][15.2]，[fptk=][1 860 MPa]， 张拉控制应力[σcon=][0.75fptk]，单根截面面积为140[ mm2]。混凝土强度均为C50，轴心抗压强度为23.1[ N/mm2]。8根构件的具体试验参数如表2所示。

本试验采用三等分点受弯加载，预应力筋的应力增量选用MGH型锚索测力传感器测量，在每根受拉钢筋的跨中和四分点处布置4个钢筋应变片，在梁的两端支座处、四分点处、跨中位置处各架设一块电阻式位移计，测点布置如图4所示。

3.2 试验结果分析

3.2.1 极限应力增量与跨中挠度之间的关系

试验所用8根无粘结预应力混凝土梁的跨中挠度实测值与预应力筋极限应力增量实测值的数据，如图5所示。

由图5数据可知，在构件几何尺寸一定的情况下，除了刚开始加载时，无粘结预应力筋的应力增长略微滞后，之后无粘结预应力筋极限应力增量的增长与跨中挠度基本表现为线性关系。说明基于结构整体变形的极限应力增量的计算方法具有较高可信度。

3.2.2 挠度计算方法的对比

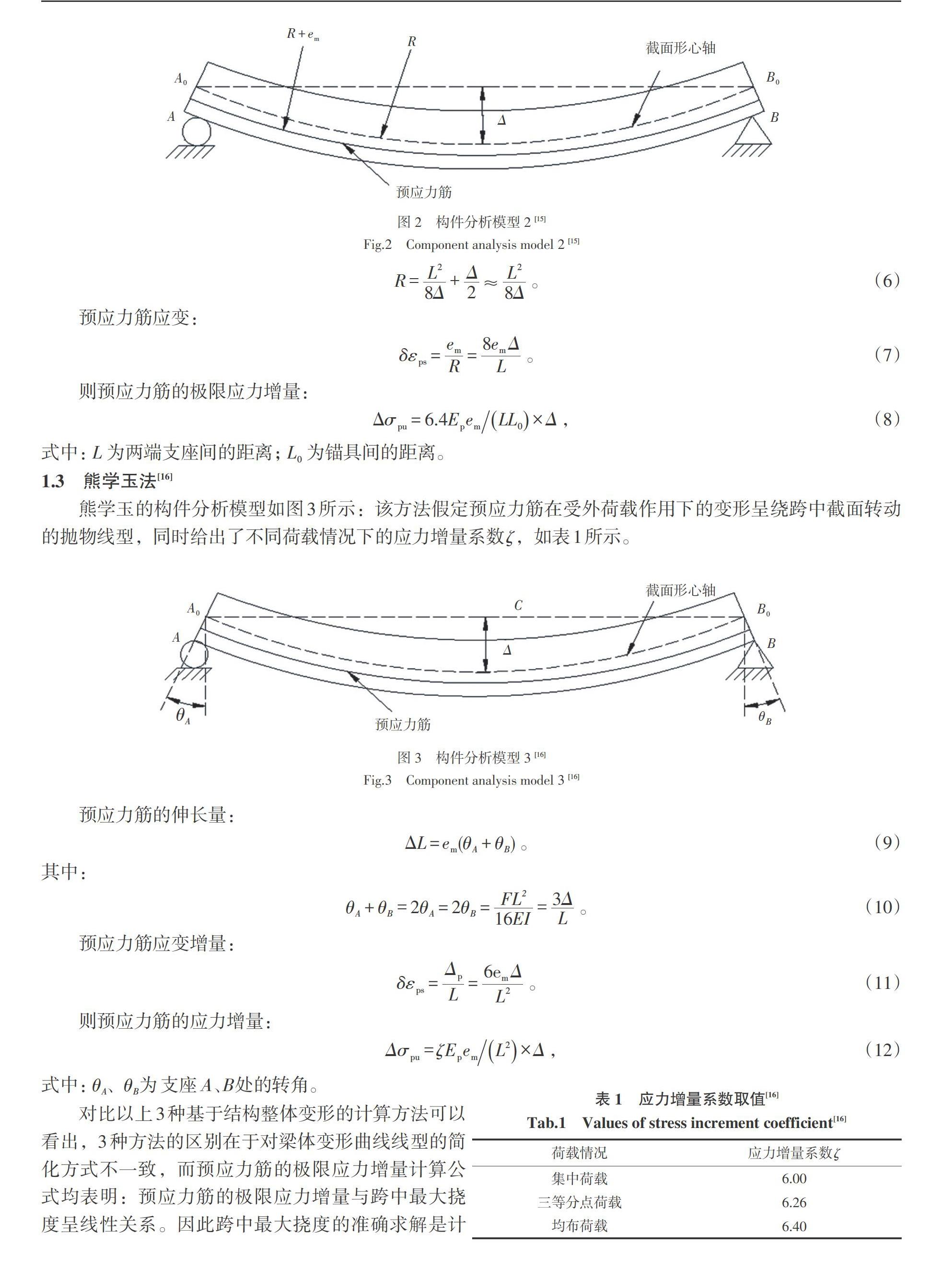
各个计算方法与实测挠度值的对比结果如表3所示，其中[Δs]為实测挠度值，[Δj1]为基于有效惯性矩法计算挠度值，[Δj2]为基于双直线法计算挠度值，[Δj3]为基于统一刚度公式计算挠度值。为了统一计算标准，取受拉非预应力钢筋屈服点进行刚度计算。

计算值与实测值的离散分布如图6所示。

从表3和图6中计算值与实测挠度值的对比可以看出，实测值与基于双直线法所得挠度计算值比值的平均值为0.706，标准差为0.125，变异系数为0.177，说明按此规范计算所得挠度普遍偏大，若将其用于基于变形的极限应力增量计算中，预应力筋将承担过多的应力;实测值与基于统一刚度法计算挠度值比值的平均值为0.733，标准差为0.188，变异系数为0.256，计算值基本偏大，且离散程度较高，计算结果不稳定，通过其公式可以看出，由于部分参数依靠数据曲线回归得到，因此结果产生较大偏差;实测值与基于有效惯性矩法计算挠度值比值的平均值为0.951，标准差为0.168，变异系数为0.176，计算值最接近于实测挠度值，并且其变化也相对平稳，离散程度低。因此对于无粘结部分预应力混凝土构件，本文建议使用基于有效惯性矩法得到的挠度计算值。

4 极限应力增量计算方法对比

本文选取了4个国家的5种规范[3，5-8]及基于整体变形的3种方法[14-16]进行极限应力增量的计算对比，如表4所示。计算结果见表5和表6。

由表5和表6相关数据可知，实测值与中国规范JGJ92—2016计算值比值的平均值为1.828、标准差为0.288、变异系数为0.157，实测值与美国规范ACI318-11计算值比值的平均值为1.438、标准差为0.232、变异系数为0.161，两部规范极限应力的计算值均小于实测值，计算偏于保守，容易造成对材料性能的使用不充分而产生浪费。实测值与加拿大规范A23.3-04计算值比值的平均值为0.771、标准差为0.116、变异系数为0.151，实测值与英国规范BS8110—1997计算值比值的平均值为0.826、标准差为0.152、变异系数为0.184，这两部规范极限应力增量的计算值大于实测值，主要是由于计算公式依赖经验建立且变量多与材料本身相关，其结果容易造成对极限应力增量的评估过高从而影响构件的安全性能相关设计。实测值与美国规范AASHTO2017计算值比值的平均值为1.004、标准差为0.199、变异系数为0.198，该部规范极限应力增量计算值与实测值基本相同，虽然均值良好，但变异程度较大，以均数为准的离散程度较高。

3种基于整体结构变形的极限应力增量的计算方法中，实测值与杜进生法计算值比值的平均值为1.741、标准差为0.181、变异系数为0.104，表明该法计算值要小于实测值，计算偏于保守，通过其计算公式可以看出，产生较大误差的主要原因是由于将挠曲线视为双折线，小于实际挠曲线的长度。实测值与王景全法计算值比值的平均值为1.088、标准差为0.113、变异系数为0.104，实测值与熊学玉法计算值比值的平均值为1.039、标准差为0.108、变异系数为0.104，这两种方法的计算值均与实测值相近，且离散程度较小，计算结果具有较高的准确度。

综上所述，基于结构整体变形的计算方法可以极大简化求解极限应力增量的计算过程，通过试验数据的整理和分析也可以看出，此种方法的计算值较为精确，具有较高的可信度。

5 结论

1）基于结构整体变形的极限应力增量的方法计算简便且具有较高精度，本文通过试验数据的对比分析为此结论提供了支持。但是此方法的精度取决于挠曲线的类比选取，挠曲线表达的越精准，计算求得的结果越趋近于实测值。

2）本文同时对基于结构整体变形的极限应力增量的方法中的关键参数挠度进行了3种计算方法的对比，其中基于有效惯性矩法求得的挠度计算精度最高且离散程度小，可以作为最终结果代入至基于变形的极限应力增量计算公式中。

参考文献：

[1]    杜进生. 无粘结预应力混凝土结构：试验、理论及应用[M]. 北京：机械工业出版社，2012：1-2.

[2]    中华人民共和国住房和城乡建设部. GB 50010—2010，混凝土结构设计规范[S]. 北京：中国建筑工业出版社，2011.

[3]    中华人民共和国住房和城乡建设部. JGJ 92—2016，无粘结预应力混凝土结构技术规程[S]. 北京：中国建筑工业出版社，2016.

[4]    AASHTO LRFD 1994，Bridge design specifications[S].

[5]    AASHTO LRFD 2017，Bridge design specifications[S].

[6]    ACI318-11，Building code requirements for structural concrete and commentary[S].

[7]    A23. 3-04，Design of concrete structures[S].

[8]    BS8110-1-1997，Structural use of concrete-part1：code of practice for design and construction[S].

[9]    BAKER A L L. A plastic theory of design for ordinary reinforced and prestressed concrete including moment re-distribution in continuous members[J]. Magazine of Concrete Research，1949，1（2）：57-66.

[10]  NAAMAN A E，ALKHAIRI F M. Stress at unbonded post-tensioned tendons：Part2-proposed methodology[J]. ACI Structural Journal，1991，88（6）：683-692.

[11]  杜進生，区达光. 体外预应力筋的极限应力：既有典型计算方法评述[J]. 工程力学，2010，27（9）：63-68.

[12]  HARAJLI M H. Effect of span-depth ratio on the ultimate steel stress in unbonded prestressed concrete members[J]. Structural Journal，1990，87（3）：305-312.

[13]  PANNELL F N. The ultimate moment of resistance of unbonded prestressed concrete beams[J]. Magazine of Concrete Research，1969，21（66）：43-54.

[14]  杜进生，刘西拉. 基于结构变形的无粘结预应力筋应力变化研究[J]. 土木工程学报，2003，36（8）：12-19.

[15]  王景全，刘钊，吕志涛. 基于挠度的体外与体内无粘结预应力筋应力增量[J]. 东南大学学报（自然科学版），2005，35（6）：915-919.

[16]  熊学玉，巫韬. 基于整体变形的部分预应力混凝土梁无粘结筋极限应力增量研究[J]. 建筑结构，2018，48（8）：24-28.

[17]  周建民，陈硕，王晓锋，等. 高强钢筋混凝土梁短期变形计算方法研究[J]. 同济大学学报（自然科学版），2013，41（4）：503-509.

[18]  周建民，董理. 配置高强钢筋混凝土梁抗弯刚度的研究[J]. 佳木斯大学学报（自然科学版），2010，28（6）：842-848.

[19]  周建民，朱军，朱顺宪. 混凝土梁裂缝宽度、刚度的统一计算方法及应用[J]. 铁道学报，2000，22（增刊1）：62-66.

[20]  BRANSON D E，TROST H. Unified procedures for predicting the deflection and centroidal axis location of partially cracked non-prestressed and prestressed concrete members[J]. ACI Journal，1982，79（2）：119-130.

[21]  杜进生，区达光. UPPC梁的开裂截面惯性矩及挠度计算研究[J]. 工程力学，2014，31（2）：170-176.