基于稀疏表示的无线传感器网络数据汇聚研究进展

何静飞 张潇月 周亚同

摘要 随物联网战略地位和影响力的不断提升，无线传感器网络（Wireless Sensor Networks， WSNs）作为物联网核心技术之一，迎来了一场新的研究热潮。如何降低网络能耗，延长网络生命周期一直是WSNs研究的关键问题。近年来，随压缩感知及低秩理论的提出，基于数据稀疏表示的WSNs数据汇聚方法受到广泛关注。利用WSNs数据的高度时空冗余特性，可有效降低数据传输量，降低网络能耗。本文从几个方面介绍现有基于数据稀疏表示的WSNs数据汇聚方法：首先，介绍压缩感知理论模型及压缩数据汇聚框架，分别从稠密随机投影和稀疏随机投影角度介绍基于压缩感知的数据汇聚方法;然后，介绍矩阵补全理论模型和基于矩阵补全的数据汇聚及重建方法;最后，提出无线传感器网络数据汇聚存在的问题和对未来研究趋势的展望。

关 键 词 无线传感器网络;稀疏表示;压缩感知;矩阵补全;数据收集;时空相关性

中图分类号 TP212.9;TN929.5     文献标志码 A

Abstract With continuous improving of the strategic position and influence of Internet of Things， Wireless Sensor Networks （WSNs）， as one of the core technologies of Internet of Things， has become a research focus. So how to reduce the network energy consumption and prolong the network lifetime has been a key research issue in WSNs. Recently， with the development of compressed sensing and low rank theory， the data aggregation method based on sparse representation in WSNs has attracted much attention. By exploiting the high spatiotemporal redundancy of WSNs data， the amount of data transmitted is effectively reduced and network energy consumption is reduced. This paper introduces the existing data aggregation methods of WSNs based on sparse representation. First， compressed sensing model and compressed data collection framework are introduced. Specifically， data aggregation methods based on compressed sensing are introduced from the perspectives of dense random projection and sparse random projection. Then matrix completion model and data aggregation and reconstruction methods based on matrix completion are discussed. Finally， the existing problems of data aggregation in WSNs and the prospect of future research are mentioned.

Key words wireless sensor network; sparse representation; compressed sensing; matrix completion; data gathering; spatio-temporal correlation

0 引言

能量消耗是無线传感器网络（Wireless Sensor Networks， WSNs）[1]中最为重要的问题。随着压缩感知和低秩理论的提出，基于稀疏表示的WSNs数据汇聚方法受到科研人员的广泛关注。通过利用WSNs数据的高度时空冗余性来有效降低数据传输量，基于稀疏表示的WSNs数据汇聚方法取得了巨大的成果。鉴于此，本文系统的对基于稀疏表示的WSNs数据汇聚方法进行分类介绍。

1 介绍

伴随着信息时代的到来，物联网（Internet of Things， IoT）[2]这一新兴信息产业迎来了发展的热潮，并逐渐改变着人们的生活方式。无线传感器网络是物联网的核心技术之一，因物联网的迅速发展而受到研究人员广泛的关注，开启了无线传感器网络发展的新纪元。

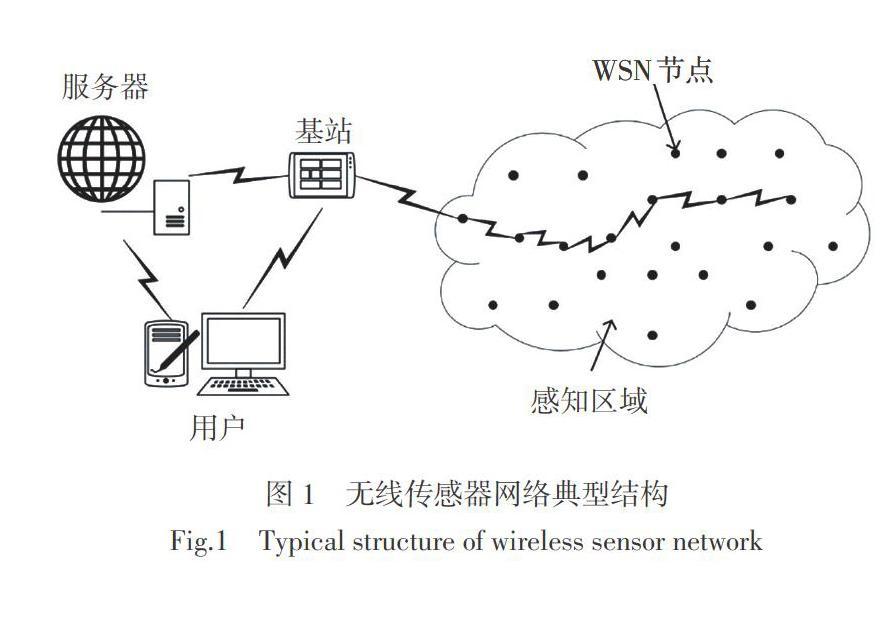
WSNs由基站和大量传感器节点构成，采用自组织方式连接。如图1所示，传感器节点部署在探测区域内，采用多跳方式将感知数据发送至基站，基站将数据处理后提供给用户使用。WSNs因具有独立的数据采集、处理和传输能力，被广泛应用在各个领域，包括军事国防[3]、环境监测[4]、健康医疗[5]和工农业[6]等。随着社会生产和日常生活对WSNs需求的增加，如何大规模高密度的部署WSNs成为研究热点。然而WSNs中网络能耗不均匀导致部分节点过早死亡，节点容量、数据处理和存储能力有限等问题，阻碍着WSNs的大规模高密度部署。近年来，随信号处理领域中压缩感知（Compressed Sensing， CS）[7-8]及低秩理论[9-10]的提出与发展，基于稀疏表示的WSNs数据汇聚方法因采用的信号处理方式能够有效降低网络能耗而受到广泛关注。根据现有研究，基于稀疏表示的WSNs数据汇聚方法可分为两大类：1）基于约束数据一阶稀疏性，即压缩感知;2）基于约束数据二阶稀疏性，即低秩约束。

在实际应用部署中，WSNs中大量传感器节点密集分布在一定区域内，节点在一段连续时间内感知的数据往往具有很高的时空冗余度，在特定稀疏基下具有稀疏性，符合CS的应用前提。因此，CS的提出开启了WSNs数据汇聚方法的新篇章。基于CS的WSNs数据汇聚方法允许网络以低于奈奎斯特频率的方式采集数据，将采集与压缩同时进行，通过减少WSNs数据传输量降低网络能耗。基于CS的WSNs数据汇聚方法受到了广泛关注并取得了巨大成功。受CS理论的推动，本质为约束数据二阶稀疏性的低秩矩阵模型[9， 10]随之兴起，并由此系统地发展出了新的理论与应用。而后，科研人员将低秩矩阵应用到WSNs中，基于低秩矩阵的数据汇聚方法是将WSNs中不同节点在不同时刻采集的数据分布到一个环境矩阵中，通过稀疏采样方式仅采集部分数据，由部分数据重建出原始数据。该过程在数学形式上是一个矩阵补全（Matrix Completion， MC）问题。由于数据本身具有时空相关性，因此基站可通过约束矩阵低秩性恢复原始数据矩阵。相比较于CS，基于MC的数据汇聚方法更有效地利用了WSNs数据的时空相关性，能够获得更高的数据重建精度，因此更加受到科研人员的关注。

本文将系统地介绍现有基于数据稀疏表示的WSNs数据汇聚方法，第2节将介绍压缩感知理论及基于压缩感知的WSNs数据汇聚方法，第3节介绍矩阵补全及基于矩阵补全的数据汇聚和重建方法，第4节对基于数据稀疏表示的WSNs数据汇聚方法的研究前景进行展望，第5节进行总结。

2 基于压缩感知的数据汇聚

2.1 压缩感知基本理论

压缩感知理论于2006年由Donoho[8]， Cands[7]等提出，其核心思想是将采样和压缩同时进行。在压缩感知框架中，原始信号[x∈?n×1]为稀疏信号或可稀疏信号，通过测量矩阵[Φ∈?m×n]可获得测量值[y=Φx∈?m×1]，这里[m?n]。由测量值[y]即可通过重构算法重建出原始信号[x]，即求解如式（1）的[?0]最小化问题：

式中，[ψ∈?n×n]为稀疏基矩阵，CS理论通过约束原始信号[x]在一定稀疏基[ψ]下的稀疏性，实现欠定问题的求解。然而[?0]范数问题的求解是一个NP-hard（Nondeterministic Polynomial-time Hard）问题[11]，由于[?1]范数是[?0]范数的凸包络，式（1）可转化为约束[?1]范数最小化[12]：

式（2）为凸优化问题，因此数据的重构过程转换为求解一线性优化问题。CS中的数据重构算法包括凸松弛类算法[13]、贪婪类算法[14-15]和迭代阈值类算法[16]。

2.2 压缩数据收集框架的建立

实际中，WSNs采集到的数据因节点部署密集具有较高的时空相关性，在一定稀疏基下呈现稀疏性，为可稀疏信号。鉴于此，科研学者尝试将CS理论应用于WSNs数据汇聚中，并取得了一定成功。而后，众多基于CS的WSNs数据汇聚方法应运而生[17-20]。

受到无线通信和CS理论研究启发，文献[21]首次将CS理论应用到WSNs中，提出压缩无线传感的概念（Compressive Wireless Sensing， CWS），用于估计具有某种结构规律的传感器数据能量有效性。文献[22]首次将CS理论应用到大规模WSNs数据汇聚中，提出了压缩数据采集模型（Compressive Data Gathering， CDG），为WSNs中的数据汇聚方法开辟了一条新道路。

图2a）为无压缩数据汇聚方法中通过多跳方式将节点数据转发到基站的直观图，节点[N1]将其感知数据[x1]发送到[N2]，[N2]将其感知数据[x2]和接收到的[x1]发送到[N3]，以此类推。在路由结束时，[Nn]将[n]个数据发送到基站。可见，距离基站越近的节点消耗能量越多，网络存在能耗不均匀情况，整体数据传输量为[n（n+1）2]。图2b）展示了CDG数据传输方式，节点[N1]产生一个随机向量[φ1=（?11，?21，…，?m1）∈?m×1]，将其感知数据[x1]乘以[φ1]后發送到[N2]。[N2]接收到数据后，将其自身感知数据[x2]乘以随机向量[φ2]后将[x1φ1+x2φ2]发送到[N3]，以此类推。第[i]个节点[Ni]所需传输数据为[j=1ixjφj]，网络整体数据传输量为[mn]。相较于无压缩采集数据方法，CDG中每个节点传输的数据是相同长度的，能够均衡网络中的能量消耗，避免因少数节点过早死亡减少网络的生命周期，同时降低了网络整体数据传输量。图3a）展示了CDG使用树形拓扑结构传输数据的路由图，其中假设测量值维数为5。

而后，文献[23]对CDG进行改进，提出IR-CDG传输机制，采用[Φ=I R∈?M×N]形式的测量矩阵，其中[I]为单位矩阵，[R∈?M×（N-M）]为高斯随机矩阵，[Φ]结构如式（3）：

该测量矩阵具有良好的约束等距性原则（Restricted Isometry Property， RIP），在保证数据可靠性的情况下，可通过减少参与传输节点的方式来降低通信成本，但单个测量值的收集需要传输的数据量仍然与CDG相同。文献[24]再次对CDG做出改进，提出一种混合压缩感知（Hybrid-CS）数据采集方法。如图3b）所示，Hybrid-CS中只有当转发量大于自身测量值的维数时才进行加权处理，否则直接转发自身测量值到父节点即可，以此减少单个测量值收集时需要传输的数据量。

随着研究的逐渐深入，越来越多的基于CS的数据汇聚方法被提出。这些方法根据测量矩阵类型可分为两大类：1）基于稠密投影的WSNs数据汇聚方法，前面所述的CDG即为该类代表性方法，其特点在于测量矩阵中元素值几乎全不为零值;2）基于稀疏投影的WSNs数据汇聚方法，IR-CDG可认为是该类方法的雏形，其特点在于测量矩阵中元素值存在一定数量的零值。如图3c）所示，在一次数据采集时隙中，只有5个节点进行数据采集，其他节点处于休眠状态，以此来降低网络能耗。后续将分别介绍基于稠密投影和基于稀疏投影的WSNs数据汇聚方法。

2.3 基于稠密投影的WSNs数据汇聚方法

通过上述的CDG及其改进算法可看出，CDG框架是通过减少数据传输量來降低能耗，延长网络寿命。而后，多种基于稠密随机投影的数据汇聚方法相继提出。

其中，部分文献从路由优化方面对数据汇聚算法进行改进[25-28]。针对同构网络，文献[25]提出了一种适用于CS的分布式数据汇聚方案，该方案中每个传感器节点独立地找到其父节点并构造路由树的一部分，而不需要中心单元来构造所有转发树。考虑到能量消耗对数据汇聚的影响，文献[26]提出基于能量感知的CS数据汇聚和能量平衡的高层数据聚合树两种数据汇聚方法，在平衡节点间能量消耗的同时提高了网络的生存周期。为解决传统的基于CS的数据汇聚方案不适用于异构WSNs的问题，文献[27]提出一种基于CS的聚类、非均匀分层、多跳路由算法。采用改进的LEACH协议实现簇间传输和融合，然后采用非均匀分层多跳路由将融合后的数据包转发到基站进行数据重建。

为提高CS数据汇聚算法中的重建精度，众多关于重建算法的研究文献相继发表。文献[29]提出双层压缩聚合（Dual-lEvel Compressed Aggregation， DECA）技术。DECA分为两个层级重建数据，在第一级使用基于扩散小波的CS来重建数据。在第二级，DECA使用矩阵补全对第一级的结果数据再次进行重建。文献[30]提出一种基于联合稀疏性的压缩感知技术，采用贝叶斯推理来建立信号的概率模型。在该贝叶斯推理恢复框架中，使用置信传播算法作为解码方法来压缩和重建空间相关信号。

此外，部分研究通过利用WSNs信号中的其他特性，进一步提高数据的重建精度。文献[31]将自回归模型引入到感知数据重建中，利用感知数据的局部相关性，实现了感知数据的局部自适应稀疏性。通过调整目标函数中的自回归参数使得数据重建适应于感知到的数据，并且根据数据的变化自适应的调节所感测数据需要的测量次数。文献[32]将全变分（Total Variation，TV）模型引入到CDG中，利用WSNs数据在不同方向上梯度的稀疏性，提出一种压缩的多时隙数据采集方法来采集任意数量的数据。然后利用TV正则化方法构造数据重建算法，并提出一种交替最小化方法来求解重建算法。

2.4 基于稀疏投影的WSNs数据汇聚方法

基于CS的数据汇聚方法中的数据传输量取决于测量矩阵，相对于稠密随机矩阵，稀疏随机投影矩阵中大部分元素值为零值，零值元素对应位置的节点数据无需转发，因此数据传输能耗大大降低。

文献[19]针对树型拓扑网络，提出最稀疏测量矩阵，该矩阵中每一行只有一个非零项，将单个测量值所需的节点数量降到最低。针对集群型网络，多种数据汇聚方法相继提出[33-35]，文献[33]提出一种最稀疏数据采集方案，该方案中只有节点的一个随机子集收集数据，每个节点的感知数据被视为一次测量值。文献[34]提出一种空间相关的基站辅助集群，在该集群中仅簇头感知数据，然后将数据传输到基站，不产生簇内的通信开销。然而，网络中常因链路不可靠导致数据丢失，现有方法通常直接将测量矩阵与网络路由被动匹配，这样会使得参与单个测量值的节点过多，测量值易受网络丢包影响。为减少网络丢包对测量值的破坏，文献[36]提出一种联合路由的稀疏随机投影数据汇聚方案，该方案先是依据路由设计稀疏投影矩阵来减少丢失数据对测量值的损毁，然后设计稀疏投影矩阵约束下的低相干稀疏表示基来确保数据的重建精度。

为达到数据汇聚算法自适应于网络，根据网络的变化改变参数来提高采样质量的目的，许多自适应算法相继提出[20，37-39]。为自适应调整取样率，文献[37]提出一种基于自适应CS的WSNs样本调度机制，该机制在每个采样窗口的基础上，根据给定的传感质量估计所需的最小采样率，并相应地调整传感器的采样率。文献[39]提出一种自适应压缩传感数据汇聚方案，只需对少量测量数据重新采样，即可确定当前稀疏度和新的采样率。为提高重建算法的恢复性能和收敛速度，提出了一种结合稀疏自适应匹配追踪算法的自适应步长变化算法。

考虑到使用CS收集数据时，WSNs的拓扑结构和路由机制也是需要关注的重点问题，多篇相关研究相继提出。文献[40]提出最小生成树的投影（Minimum Spanning Tree Projection， MSTP），该方法中以随机选择的投影节点为根，组建一个最小生成树（Minimum-Spanning-Trees， MSTs），每个投影节点将接收的数据的加权和发送到基站。针对集群式WSNs，文献[41]利用随机采样和随机游走相结合的方式构造稀疏的二值感知矩阵。CS用来收集WSNs中空间域的感知数据，随机抽样和随机游走分别用来选择集群和簇头中的感知数据。而后，文献[42]中进一步改进，随机抽样和随机游走分别在时间域和空间域采集数据。文献[43]提出一种同时利用时空相关性的结合Kronecker压缩感知和簇拓扑结构的数据汇聚方法，簇头基于收集的数据生成稀疏的自测量矩阵，基站将这些矩阵构造为块对角矩阵，以利用簇间的空间相关性。

相较于稠密投影，基于稀疏投影的WSNs数据汇聚方法更加节能网络能耗，因此受到研究人员的青睐。

3 低秩理论在WSNs数据汇聚中的研究

3.1 矩阵补全基本理论

受压缩感知理论取得的巨大成功的推动，本质为约束数据二阶稀疏性的低秩矩阵模型[9，44]近年来获得研究人员的关注。低秩矩阵模型中一个典型应用即为矩阵补全，当矩阵[M∈?m×n]中仅有部分观测数据已知，而其他数据均缺少时，利用部分观测数据恢复出矩阵[M]的过程即为矩阵补全。如同压缩感知的前提是数据稀疏性，矩阵补全的前提是矩阵低秩性。通过约束矩阵的秩，恢复出原始矩阵：

式中：[X]为决策矩阵;[rankX]表示矩阵[X]的秩;[Π]代表矩阵中观测到的数据所在位置索引的集合。类似于向量中[?0]最小化问题，矩阵秩最小化问题也是一个NP-hard问题。上述压缩感知中采用[?1]范数替代[?0]范数，这里，可采用核范数替代秩最小化问题[45]，式（5）可转化为

式中[·*]为核范数，即矩阵的奇异值之和。低秩矩阵模型目前已广泛应用在信号处理和机器学习等领域。由于WSNs中不同节点在不同采集时刻获取的数据可构成矩阵形式，数据的时空相关性使得矩阵呈现低秩特性，为矩阵补全应用到WSNs数据汇聚提供了前提条件。

3.2 WSNs数据的时空相关性

WSNs环境感知由密集部署在一定区域的节点完成，可监测风力、温度、湿度、光照等环境信息。假设一个WSN由一个基站和[n]个传感器节点组成，用[N1，N2，…，Nn]表示节点序号，节点每隔时间[τ]感知一次数据并传输到基站，因此在[mτ]的时间范围内，由[n]个节点采集到的[m×n]个数据可组成环境矩阵[M]：

如图4所示，[M]的行由同一节点在不同采集时刻的感知数据组成，列由不同节点在同一时刻的感知数据组成。由于节点分布密集，数据采集时刻间隔短，邻近节点在相邻时刻感知到的数据往往波动很小，即这些数据通常具有较高的时空相关性。也就是说[M]具有低秩特性，符合矩阵补全应用的前提。因此可通过稀疏采样收集数据，然后基于矩阵补全对缺失数据进行重建，以此来降低网络能耗。

3.3 基于矩阵补全的WSNs数据汇聚方法

因WSNs数据具有低秩性，满足矩阵补全理论应用的前提，近年来研究人员将MC成功应用于WSNs的数据汇聚与重建中[46-56]。

2010年，Cheng等[48]首次将MC应用到WSNs数据汇聚中，提出Efficient Data Gathering Approach （EDCA）。为减少网络能耗，随机选择部分节点进行数据感知，而后将数据直接发送到基站。数据重建上，EDCA将MC中秩最小化问题转换为凸优化问题。通过稀疏采样方式减少了网络数据传输量，在一定程度上降低了网络能耗。然而当采样率极低时，稀疏采样构成的矩阵存在空列的概率极高，此时采用EDCA会导致较大的数据重建误差。为解决这个问题，文献[49]提出Spatio-Temporal Compressive Data Collection （STCDG）方法，同时利用矩阵的低秩性和数据短时间内稳定性进一步降低数据传输量。针对降低采样率导致的空列问题，STDCG在重构矩阵时会先删除空列，只恢复非空列，然后使用基于时间稳定性的优化技术恢复空列，以此来提高数据的重建精度。在进一步利用信号时空相关性的全局和局部相关特性基础上，文献[57]提出一种基于低阶差分平滑度的数据重建算法，将时变图形信号的差分平滑先验引入到时空信号分析领域。

而后，为进一步提高数据重建精度，降低网络数据传输量，多篇相关研究相继提出。文献[50]通过对WSNs数据稀疏性和低秩性的研究，提出一种联合稀疏约束和低秩约束的无线传感器网络数据汇聚重建模型，并提出基于加性半二次正则化方法的重构算法，保证了数据重建的运算速度與准确性。文献[58]提出一种负载均衡的随机采样机制，通过变动的采样率在确保重建精度的前提下降低网络能耗，同时利用快速奇异值阈值算法提高了重建速度。

在WSNs数据汇聚方法上，文献[51]通过引入历史数据，将MC与CDG算法相结合，在CDG数据汇聚框架下，约束历史数据与当前时刻数据构成矩阵的低秩性，在CDG数据汇聚框架下大幅度提高了数据重建精度。文献[52]提出一种基于MC的实时数据汇聚方法（MC-Weather）。该方法包括一种基于三种样本学习原则的自适应采样算法，能够快速找到一个适用于矩阵补全的稀疏采样数据集。MC-Weather在动态环境中以较低的通信成本成功实现了更高的数据重建精度。文献[59]提出一种适用于集群型网络的实时稀疏数据汇聚重建方法，所提出的稀疏汇聚方案实现了存在部分节点休眠情况下的数据汇聚，通过先前重建数据估计出代表空间分布的子空间，结合全变分约束实现了实时WSNs数据的高精度重建。

同时，鉴于矩阵补全的特征，科研学者也将其应用到WSNs数据丢失和损坏中。在WSNs中，受硬件和无线条件的影响，原始感知数据通常会出现明显的数据丢失和损坏。文献[60]提出一种基于稀疏表示的大量缺失数据重建方法，分析并利用感知数据的时间稳定性、空间相关性及低秩特性，针对不同的数据丢失模式进行分析并获得了较好的重建精度。而后，文献[61]进一步完善方法，考虑多参量数据间同样具有较强的相关性，增加了多参量数据约束来利用该特征，进一步提高了重建精度。考虑到WSNs不仅存在丢失，同时还存在异常值，文献[54]提出了一种基于MC的两阶段数据恢复方案（MC-two-phase），该方案利用MC技术，充分利用环境数据的固有特性，恢复存在数据丢失或损坏问题的数据矩阵。为了能在恢复丢失及异常数据的同时检测出异常节点的位置，文献[62]基于环境数据的低阶特征，提出一种基于结构噪声矩阵补全的弹性网络正则化数据重建算法。

由于基于低秩矩阵模型的WSNs数据汇聚及重建方法能够更有效地利用WSNs数据的时空相关性，近年来相关成果相继涌现，极大的推动了WSNs数据汇聚方法的研究。

4 存在的问题及展望

压缩感知和低秩理论是近年来信号处理领域的热点研究，其本质是利用数据不同阶的稀疏性，在WSNs数据汇聚研究中也取得了很多具有突破性的进展。一般来讲，数据汇聚方法的改进主要有3个方面：重建算法的优化、变换矩阵的设计和传感矩阵的构造。然而，针对大规模、高密度的WSNs数据汇聚方法研究仍存在挑战性。首先，在部分节点处于休眠状态的情况下，如何保证感知到的数据准确地传输到基站，避免数据的丢失。其次，为减少网络能量消耗采用稀疏采样进行数据汇聚时，如何选择具有代表性的节点使得数据重建时的准确度更高仍需进一步研究。最后，在数据汇聚方案的设计上，如何防止因能量耗尽或恶意攻击而可能导致的节点故障，造成系统的鲁棒性差等技术瓶颈仍需科研人员进一步研究探索。

针对多参量异构WSNs，仅基于CS与低秩矩阵虽可有效利用各类信号的时空冗余性，却忽略了各类型感知信号数据间的相关性。多参量异构WSNs中不同节点，不同采集时刻及不同类型的感知数据呈现三维特性，如进一步考虑节点的空间位置，可呈现更高维特性。此时，所需处理的高维数据采用二维矩阵的形式并不足以刻画其复杂的内在结构。近年来，张量[63]作为向量、矩阵的高阶拓展，能直接表示高维数据，能够更好地刻画高维数据的内在相关性，对高维数据处理具有明显的优势，受到了研究人员的重点关注，目前已成功地应用于高维信号处理、计算机视觉、机器学习等领域[64-70]，为有效利用多参量异构WSNs中数据间相关性提供了一种全新的技术手段。目前存在多种张量分解形式，典型的有CANDECOMP/PARAFAC （CP）[71]分解，Tucker[72]分解，Tensor Singular Value Decomposition （t-SVD）[73]和Tensor-train （TT）[74]分解等。虽然基于张量的WSNs数据感知重建研究相继提出[75-77]，但其相关研究较少。将张量应用于WSNs的数据汇聚中时，数据主要按照节点感知数据的类型、分布位置和感知时间分布在张量中。基于稀疏表示的无线传感器网络通过部分采样方式获取数据，而稀疏采样的方式和与之适应的汇聚方法密不可分，如何在满足汇聚方法的前提下设计能够捕获更多数据信息的稀疏采样方式仍需进一步研究。且由于多参量异构WSNs数据的特殊性，需进一步探索适用于该高维数据的张量分解模型，以有效利用各类型感知信号数据本身的时空相关性及其之间的相关性。

大規模部署的WSNs中传感器往往因自然灾害、节点自身问题等其他事件的影响，会导致汇聚到的数据存在异常和噪声，针对异常值和噪声，可基于鲁棒主元分析（Robust PCA， RPCA）[78]进行探索，该问题同样可推广到张量模型下解决多参量异构WSNs中异常值及噪声问题。同时，WSNs数据汇聚也可采用机器学习方法[79]去除故障节点、优化簇头选择等。科研人员仍需进一步研究，以推动大规模、高密度、多参量的WSNs的实际部署和高效的数据汇聚。

5 结语

无线传感器网络中，基于稀疏表示的数据汇聚方法能够有效降低网络传输数据量，延长网络生命周期。本文主要介绍了基于压缩感知（约束数据一阶稀疏性）及低秩矩阵模型（约束数据二阶稀疏性）的WSNs数据汇聚方法。基于WSNs数据的时空相关性，这些方法从不同角度对WSNs数据汇聚进行了研究，致力于降低网络能耗，提高数据重建精度。同时，对当前WSNs数据汇聚中存在的问题及后续研究方向进行了探讨与展望，通过研究更高阶的张量形式进一步利用各类感知信号间相关性，切实推动大规模、高密度、多参量的WSNs的实际部署。

参考文献：

[1]    AKYILDIZ I F，SU W，SANKARASUBRAMANIAM Y，et al. Wireless sensor networks：a survey[J]. Computer Networks，2002，38（4）：393-422.

[2]    ATZORI L，IERA A，MORABITO G. The Internet of Things：a survey[J]. Computer Networks，2010，54（15）：2787-2805.

[3]    PRABHU B，PRADEEP M，GAJENDRAN E. Military Applications of Wireless Sensor Network System[J]. Scientific Digest-A Multidisciplinary Journal of Scientific Research & Education，2016，2（12）：164-168.

[4]    XU G，SHEN W，WANG X. Applications of wireless sensor networks in marine environment monitoring：a survey[J]. Sensors，2014，14（9）：16932-16954.

[5]    VO M T，THANH NGHI T T，TRAN V S，et al. Wireless sensor network for real time healthcare monitoring：network design and performance evaluation simulation[C]//5th International Conference on Biomedical Engineering in Vietnam，2015.

[6]    JAWAD H M，NORDIN R，GHARGHAN S K，et al. Energy-efficient wireless sensor networks for precision agriculture：a review[J]. Sensors，2017，17（8）：E1781.

[7]    CAND?S E. Compressive sampling[C]//Proceedings of the International Congress of Mathematicians Madrid，August 22–30，2006. Zuerich，Switzerland：European Mathematical Society Publishing House：1433-1452.

[8]    DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory，2006，52（4）：1289-1306.

[9]    CAND?S E J，RECHT B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics，2009，9（6）：717-772.

[10]  CANDES E J，PLAN Y. Matrix completion with noise[J]. Proceedings of the IEEE，2010，98（6）：925-936.

[11]  MUTHUKRISHNAN S. Data streams：algorithms and applications[J]. Foundations and Trends? in Theoretical Computer Science，2005，1（2）：117-236.

[12]  DONOHO D L. For most large underdetermined systems of linear equations the minimal[J]. Communications on Pure and Applied Mathematics：A Journal Issued by the Courant Institute of Mathematical Sciences，2006，59（6）：797-829.

[13]  CHEN S S，DONOHO D L，SAUNDERS M A. Atomic decomposition by basis pursuit[J]. SIAM Review，2001，43（1）：129-159.

[14]  NEEDELL D，TROPP J A. CoSaMP：Iterative signal recovery from incomplete and inaccurate samples[J]. Applied and Computational Harmonic Analysis，2009，26（3）：301-321.

[15]  DAI W，MILENKOVIC O. Subspace pursuit for compressive sensing signal reconstruction[J]. IEEE Transactions on Information Theory，2009，55（5）：2230-2249.

[16]  BLUMENSATH T，DAVIES M E. Iterative hard thresholding for compressed sensing[J]. Applied and Computational Harmonic Analysis，2009，27（3）：265-274.

[17]  WANG W，WANG D，JIANG Y. Energy efficient distributed compressed data gathering for sensor networks[J]. Ad Hoc Networks，2017，58：112-117.

[18]  LIANG J，MAO C C. Distributed compressive sensing in heterogeneous sensor network[J]. Signal Processing，2016，126：96-102.

[19]  WU X G，XIONG Y，YANG P L，et al. Sparsest random scheduling for compressive data gathering in wireless sensor networks[J]. IEEE Transactions on Wireless Communications，2014，13（10）：5867-5877.

[20]  RAN R，OH H. Adaptive sparse random projections for wireless sensor networks with energy harvesting constraints[J]. EURASIP Journal on Wireless Communications and Networking，2015，2015（1）：1-10.

[21]  BAJWA W，HAUPT J，SAYEED A，et al. Compressive wireless sensing[C]// 5th International Conference on Information Processing in Sensor Networks. Nashville，TN，USA. IEEE，2006.

[22]  LUO C，WU F，SUN J，et al. Compressive data gathering for large-scale wireless sensor networks[C]// Proceedings of the 15th annual international conference on Mobile computing and networking. 2009：145-156.

[23]  LUO C，WU F，SUN J，et al. Efficient measurement generation and pervasive sparsity for compressive data gathering[J]. IEEE Transactions on Wireless Communications，2010，9（12）：3728-3738.

[24]  LUO J，XIANG L，ROSENBERG C. Does compressed sensing improve the throughput of wireless sensor networks？[C]// IEEE International Conference on Communications. May 23-27，2010，Cape Town，South Africa. IEEE，2010：1-6.

[25]  EBRAHIMI D，ASSI C. A distributed method for compressive data gathering in wireless sensor networks[J]. IEEE Communications Letters，2014，18（4）：624-627.

[26]  PAKDAMAN TIRANI S，AVOKH A. On the performance of sink placement in WSNs considering energy-balanced compressive sensing-based data aggregation[J]. Journal of Network and Computer Applications，2018，107：38-55.

[27]  LI B，YANG H J，LIU G L，et al. An energy-efficient routing algorithm in three-dimensional underwater sensor networks based on compressed sensing[J]. Information，2017，8（2）：66.

[28]  ALAGIRISAMY M，CHOW C O，NOORDIN K A B. Compressive sensing with perceptron based routing for varying traffic intensity based on capsule networks[J]. Computers & Electrical Engineering，2019，79：106446.

[29]  XIANG L，LUO J，DENG C W，et al. Dual-level compressed aggregation：recovering fields of physical quantities from incomplete sensory data[EB/OL]. 2011

[30]  MASOUM A，MERATNIA N，HAVINGA P J M. A distributed compressive sensing technique for data gathering in wireless sensor networks[J]. Procedia Computer Science，2013，21：207-216.

[31]  JIN W，TANG S J，YIN B C，et al. Data gathering in wireless sensor networks  through  intelligent  compressive  sensing[C]//2012 Proceedings IEEE INFOCOM. March 25-30，2012，Orlando，FL，USA. IEEE，2012：603-611.

[32]  XU Y，SUN G L，GENG T，et al. Compressive multi-timeslots data gathering with total variation regularization for wireless sensor networks[J]. IEEE Communications Letters，2019，23（4）：648-651.

[33]  SUN P，WU L T，WANG Z B，et al. Sparsest random sampling for cluster-based compressive data gathering in wireless sensor networks[J]. IEEE Access，2018，6：36383-36394.

[34]  PACHARANEY U S，GUPTA R K. Clustering and compressive data gathering in wireless sensor network[J]. Wireless Personal Communications，2019，109（2）：1311-1331.

[35]  PACHARANEY U S，GUPTA R K. Cluster restructuring and compressive data gathering for transmission efficient wireless sensor network[C]//Intelligent Communication Technologies and Virtual Mobile Networks. Cham：Springer International Publishing，2019：1-18.

[36]  吳宣够，储昭斌，郑啸，等. 链路不可靠下稀疏投影无线传感器网络数据收集研究[J]. 计算机学报，2019，42（2）：388-402.

[37]  HAO J，ZHANG B X，JIAO Z Z，et al. Adaptive compressive sensing based sample scheduling mechanism for wireless sensor networks[J]. Pervasive and Mobile Computing，2015，22：113-125.

[38]  CHEN S G，LIU J C，WANG K，et al. A hierarchical adaptive spatio-temporal data compression scheme for wireless sensor networks[J]. Wireless Networks，2019，25（1）：429-438.

[39]  CHEN J，JIA J，DENG Y S，et al. Adaptive compressive sensing and data recovery for periodical monitoring wireless sensor networks[J]. Sensors，2018，18（10）：E3369.

[40]  EBRAHIMI D，ASSI C. Compressive data gathering using random projection for energy efficient wireless sensor networks[J]. Ad Hoc Networks，2014，16：105-119.

[41]  LI X L，TAO X F，MAO G Q. Unbalanced expander based compressive data gathering in clustered wireless sensor networks[J]. IEEE Access，2017，5：7553-7566.

[42]  LI X L，TAO X F，CHEN Z. Spatio-temporal compressive sensing-based data gathering in wireless sensor networks[J]. IEEE Wireless Communications Letters，2018，7（2）：198-201.

[43]  ZHANG C，LI O，TONG X，et al. Spatiotemporal data gathering based on compressive sensing in WSNs[J]. IEEE Wireless Communications Letters，2019，8（4）：1252-1255.

[44]  林宙辰，马毅. 信号与数据处理中的低秩模型—理论、算法与应用[EB/OL]. [2020-02-19] https：//wenku. baidu. com/view/51701da0e45c3b3566

ec8b0f. html.

[45]  KONISHI K，URUMA K，TAKAHASHI T，et al. Iterative partial matrix shrinkage algorithm for matrix rank minimization[J]. Signal Processing，2014，100：124-131.

[46]  陈蕾，杨庚，陈正宇，等. 基于结构化噪声矩阵补全的Web服务QoS预测[J]. 通信学报，2015，36（6）：53-63.

[47]  陈蕾，杨庚，陈正宇，等. 基于线性Bregman迭代的结构化噪声矩阵补全算法[J]. 计算机学报，2015，38（7）：1357-1371.

[48]  CHENG J，JIANG H B，MA X Q，et al. Efficient data collection with sampling in WSNs：making use of matrix completion techniques[C]//2010 IEEE Global Telecommunications Conference GLOBECOM 2010. December 6-10，2010，Miami，FL，USA. IEEE，2010：1-5.

[49]  CHENG J，YE Q，JIANG H B，et al. STCDG：an efficient data gathering algorithm based on matrix completion for wireless sensor networks[J]. IEEE Transactions on Wireless Communications，2013，12（2）：850-861.

[50]  HE J F，SUN G L，ZHANG Y，et al. Data recovery in wireless sensor networks with joint matrix completion and sparsity constraints[J]. IEEE Communications Letters，2015，19（12）：2230-2233.

[51]  HE J F，SUN G L，LI Z Z，et al. Compressive data gathering with low-rank constraints for Wireless Sensor networks[J]. Signal Processing，2017，131：73-76.

[52]  XIE K，WANG L L，WANG X，et al. Learning from the past：intelligent on-line weather monitoring based on matrix completion[C]//IEEE 34th International Conference on Distributed Computing Systems. June 30-July 3，2014，Madrid，Spain. IEEE，2014：176-185.

[53]  顧洁. 基于矩阵补全的无线传感网数据收集技术研究[D]. 南京：南京邮电大学，2018.

[54]  XIE K，NING X P，WANG X，et al. Recover corrupted data in sensor networks：a matrix completion solution[J]. IEEE Transactions on Mobile Computing，2017，16（5）：1434-1448.

[55]  TAN J W，LIU W，WANG T，et al. An adaptive collection scheme-based matrix completion for data gathering in energy-harvesting wireless sensor networks[J]. IEEE Access，2019，7：6703-6723.

[56]  KORTAS M，HABACHI O，BOUALLEGUE A，et al. The energy-aware matrix completion-based data gathering scheme for wireless sensor networks[J]. IEEE Access，2020，8：30772-30788.

[57]  MAO X H，QIU K，LI T J，et al. Spatio-temporal signal recovery based on low rank and differential smoothness[J]. IEEE Transactions on Signal Processing，2018，66（23）：6281-6296.

[58]  XU Y，SUN G L，GENG T，et al. Low-energy data collection in wireless sensor networks based on matrix completion[J]. Sensors，2019，19（4）：945.

[59]  HE J F，ZHANG X Y，ZHOU Y T，et al. A subspace approach to sparse sampling based data gathering in wireless sensor networks[J]. Sensors，2020，20（4）：985.

[60]  KONG L H，XIA M Y，LIU X Y，et al. Data loss and reconstruction in sensor networks[C]//Proceedings IEEE INFOCOM. April 14-19，2013，Turin，Italy. IEEE，2013：1654-1662.

[61]  KONG L H，XIA M Y，LIU X Y，et al. Data loss and reconstruction in wireless sensor networks[J]. IEEE Transactions on Parallel and Distributed Systems，2014，25（11）：2818-2828.

[62]  CHEN Z Y，CHEN L，HU G B，et al. Data reconstruction in wireless sensor networks from incomplete and erroneous observations[J]. IEEE Access，2018，6：45493-45503.

[63]  KOLDA T G，BADER B W. Tensor decompositions and applications[J]. SIAM Review，2009，51（3）：455-500.

[64]  LU C Y，FENG J S，CHEN Y D，et al. Tensor robust principal component analysis with a new tensor nuclear norm[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence，2020，42（4）：925-938.

[65]  LIU Y P，CHEN L X，ZHU C. Improved robust tensor principal component analysis via low-rank core matrix[J]. IEEE Journal of Selected Topics in Signal Processing，2018，12（6）：1378-1389.

[66]  CHEN Y，HUANG T Z，ZHAO X L. Destriping of multispectral remote sensing image using low-rank tensor decomposition[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing，2018，11（12）：4950-4967.

[67]  GAO S Q，FAN Q B. A mixture of nuclear norm and matrix factorization for tensor completion[J]. Journal of Scientific Computing，2018，75（1）：43-64.

[68]  JI T Y，HUANG T Z，ZHAO X L，et al. A non-convex tensor rank approximation for tensor completion[J]. Applied Mathematical Modelling，2017，48：410-422.

[69]  JIANG T X，HUANG T Z，ZHAO X L，et al. Matrix factorization for low-rank tensor completion using framelet prior[J]. Information Sciences，2018，436/437：403-417.

[70]  WANG Y T，ZHAO X L，JIANG T X，et al. A total variation and group sparsity based tensor optimization model for video rain streak removal[J]. Signal Processing：Image Communication，2019，73：96-108.

[71]  HARSHMAN R A. Foundations of the PARAFAC procedure：Model and conditions for an explanatory multi-mode factor analysis[J]. UCLA Working Papers in Phonetics，1970，16：1-84.

[72]  TUCKER L R. The extension of factor analysis to three-dimensional matrices[C]//In Frederiksen. Proceedings of the Contributions to Mathematical Psychology. Holt，Rimehat and Winston，New York，1964：279-311.

[73]  ZHANG Z M，AERON S. Exact tensor completion using t-SVD[J]. IEEE Transactions on Signal Processing，2017，65（6）：1511-1526.

[74]  OSELEDETS I V. Tensor-train decomposition[J]. SIAM Journal on Scientific Computing，2011，33（5）：2295-2317.

[75]  HE J F，ZHOU Y T，SUN G L，et al. Multi-attribute data recovery in wireless sensor networks with joint sparsity and low-rank constraints based on tensor completion[J]. IEEE Access，2019，7：135220-135230.

[76]  MILOSEVIC B，YANG J，VERMA N，et al. Efficient energy management and data recovery in sensor networks using latent variables based tensor factorization[C]//Proceedings of the 16th ACM international conference on Modeling，analysis & simulation of wireless and mobile systems. Barcelona Spain. New York，NY，USA：ACM，2013.

[77]  HE J F，SUN G L，ZHANG Y，et al. Data recovery in heterogeneous wireless sensor networks based on low-rank tensors[C]//IEEE Symposium on Computers and Communication （ISCC）. June 27-30，2016，Messina，Italy. IEEE，2016：616-620.

[78]  CHANDRASEKARAN V，SANGHAVI S，PARRILO P A，et al. Sparse and low-rank matrix decompositions[J]. IFAC Proceedings Volumes，2009，42（10）：1493-1498.

[79]  ALSHEIKH M A，LIN S W，NIYATO D，et al. Machine learning in wireless sensor networks：algorithms，strategies，and applications[J]. IEEE Communications Surveys & Tutorials，2014，16（4）：1996-2018.