危险品运输车辆路径优化问题研究综述

王能民 张萌 何正文

摘要 危险品运输是社会关注的热点之一，危险品运输车辆路径优化也是重要的研究问题。本文对现有相关研究进行整理和分类，梳理危险品运输车辆路径优化问题的研究进展。首先将危险品运输车辆路径优化研究分为4类，即单目标危险品运输路径选择研究、多目标危险品运输路径选择研究、单目标危险品运输车辆路径问题研究、多目标危险品运输车辆路径问题研究;进而分别在每类研究中梳理了从特殊约束条件、特殊风险度量、特殊网络、特殊运输条件等角度入手的研究工作，并分析了各研究的研究特色、求解方法和适用性。最后，在整理相关研究优缺点的基础上，分析了现有研究可改进和完善的内容，总结了未来研究的趋势和重要方向。

关 键 词 危险品运输;路径选择;车辆路径问题;多目标优化;综述

中图分类号 U492.81     文献标志码 A

Abstract Hazardous materials transportation is a focus of the public and vehicle routing optimization for hazardous materials transportation is a significant research problem. This paper sorts out and classifies the existing related researches， reviews the research progress of vehicle routing optimization for hazardous materials transportation. Firstly， the researches on vehicle routing optimization for hazardous materials transportation are divided into four categories： single-objective route selection， multi-objective route selection， single-objective vehicle routing problem and multi-objective vehicle routing problem. Then， the research works from the perspectives of special constraints， special risk measurements， special networks and special transportation conditions are sorted out in each category. And the research characteristics， solution methods and applicability of each research are analyzed. Finally， on the basis of sorting out the advantages and disadvantages of each research， the contents that can be improved and perfected are analyzed， and the future research trends and important directions are summarized.

Key words hazardous materials transportation; route selection; vehicle routing problem; multi-objective optimization; review

0 引言

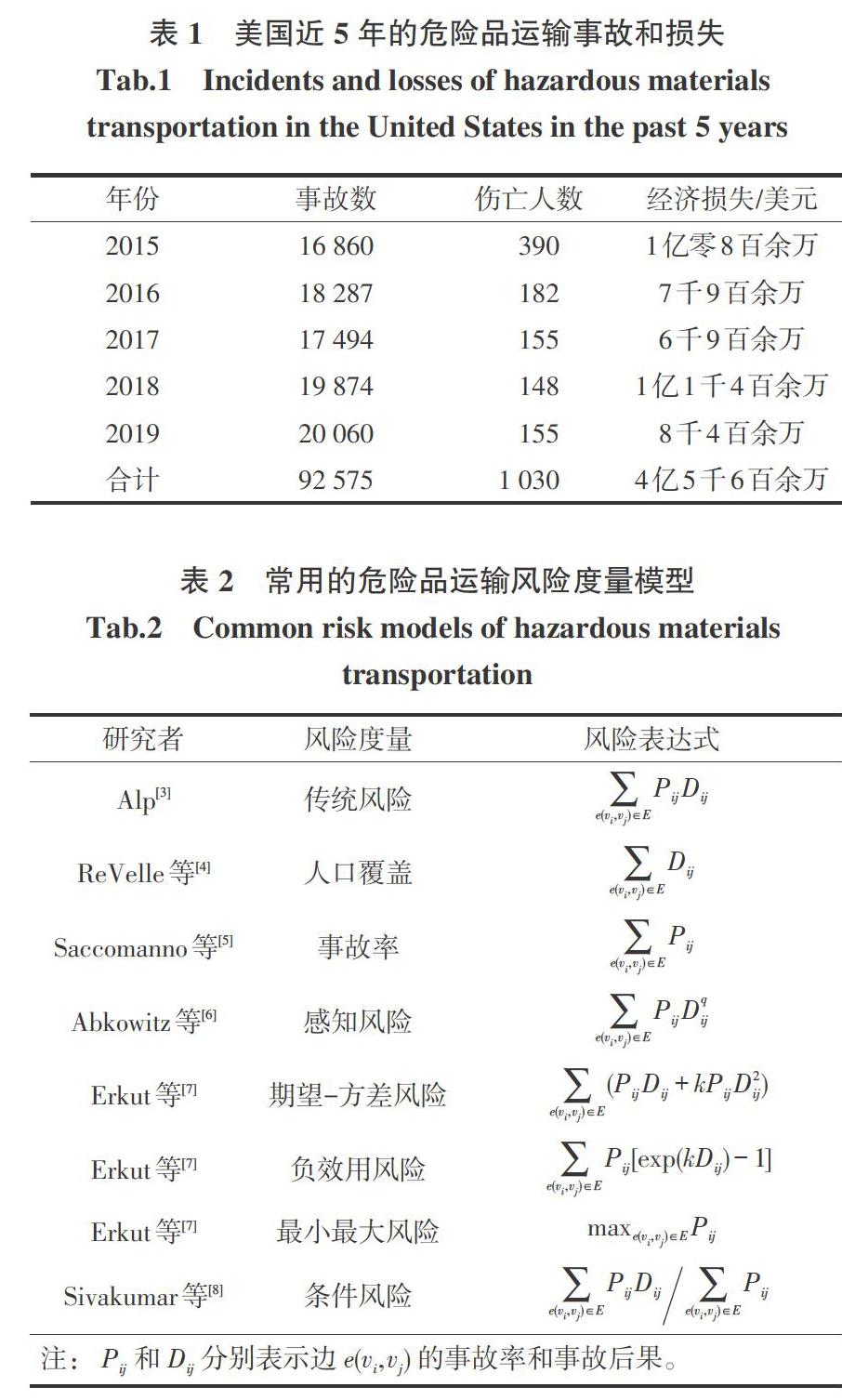
随着经济快速发展，危险品运输活动日益增多。我国危险品运量占公路运输总量的30%以上且呈现上升趋势，2017年运输量已超过16 亿t，实现大于10%的年增长[1]。危险品指易燃易爆品、危险化学品、放射性物品等能够危及人身和财产安全的物品，一旦在运输过程中发生事故会产生严重的危害。我国危险品运输事故层出不穷，例如2012年包茂高速8.26事故、2014年晋济高速3.1事故、2015年荣乌高速1.16事故等。发达国家也面临危险品运输风险的威胁，根据美国交通部统计，近5年来美国每年发生危险品运输事故上万次，伤亡数百人并造成数千万美元的经济损失，如表1所示。

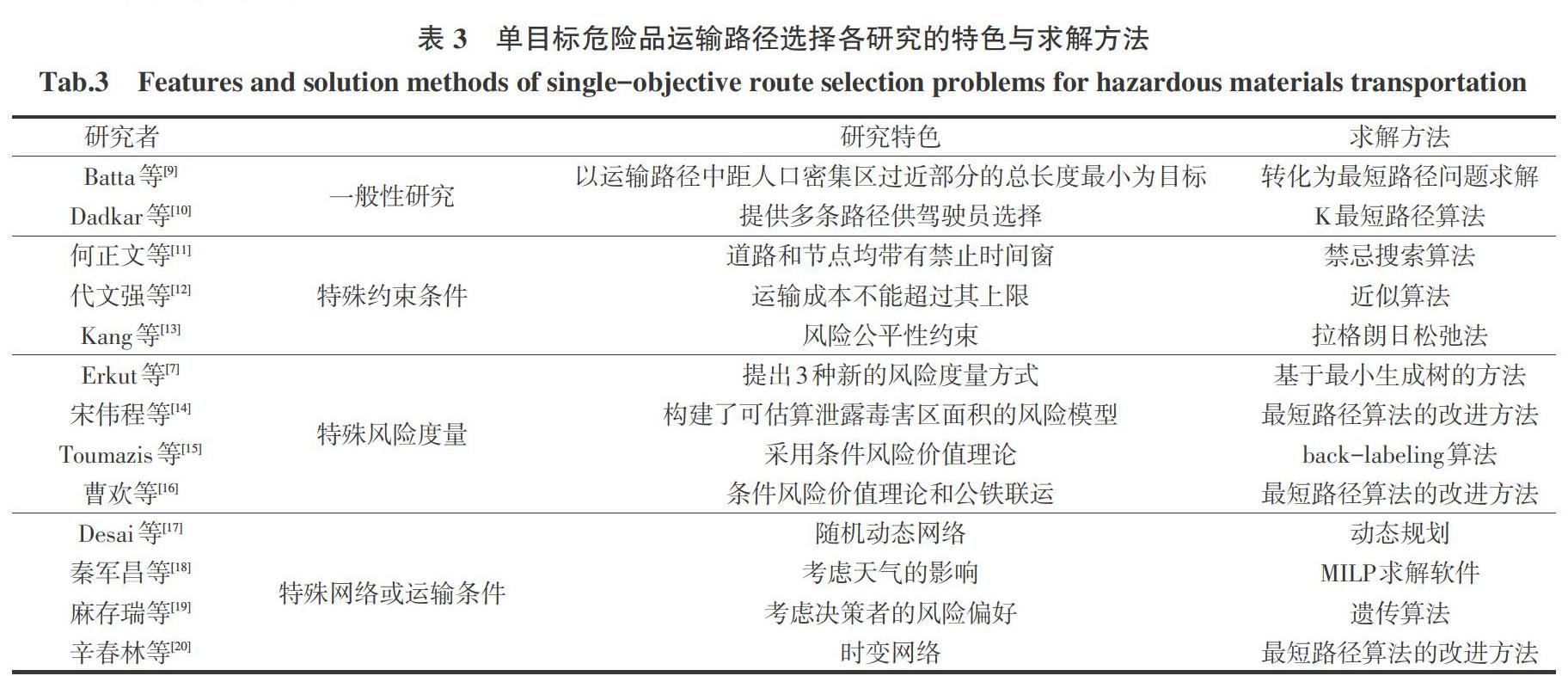
危险品运输事故频发、事故危害极大，合理的运输路径规划可在一定程度上降低风险，因此危险品运输车辆路径优化逐渐成为社会关注的热点和重要的研究问题。一部分学者致力于研究如何度量危险品的运输风险，Erkut等[2]总结了8种常见的风险度量方式，如表2所示。另一些学者则改进一般的车辆路径优化模型，研究成果主要集中于危险品运输路径选择和危险品运输车辆路径问题两方面。本文通过对现有研究进行整理和分类，梳理危险品运输车辆路径优化问题的研究进展，分析现有研究可改进和完善的内容，并探讨未来研究的趋势。

1 危险品运输路径选择研究现状

结合危险品运输和路径选择问题所进行的研究开始较早，历经多年的发展，至今仍保持一定的热度。大量学者投身于此方面的研究工作，主要形成了两类成果，其一，根据研究的需要结合现实问题的特性将一般路径选择问题的优化目标改为对运输风险的考量;其二，同时考虑运输成本（或运输时间等）最小和运输风险最小，研究多目标路径选择问题。以下将详细综述这些研究成果。

1.1 单目标危险品运输路径选择研究

早期的危险品运输路径选择研究主要针对单目标问题。Batta等[9]是较早开始研究的学者，他们针对运载“令人反感”货物的车辆，以运输路径中距人口密集区过近部分的总长度最小为目标研究路径选择问题。Dadkar等[10]从另一个角度出发，认为需为危险品的运输路径增加多样性，他们利用k最短路径算法生成可行路径集合供驾驶员进行选择，避免运输车队重复经过相同的人口密集区。还有学者还从特殊约束条件、特殊风险度量、特殊网络和特殊運输条件等角度入手，开展了一系列研究工作。

1）特殊约束条件。一些学者在研究中考虑了特殊的约束条件，例如何正文等[11]考虑道路和节点均带有禁止时间窗，以总运输时间最小为目标建立模型并设计禁忌搜索算法求解。代文强等[12]将运输成本的上限作为约束条件，研究风险最小化的路径选择问题。Kang等[13]扩展了传统的风险价值模型，建立了不确定性条件下带有风险公平性约束的路径选择模型，并且考虑了需运输的危险品有多个品种的情况。

2）特殊风险度量。运输风险的度量方式也是学者们的探索方向。Erkut等[7]提出期望-方差风险、负效用风险、最小最大风险这3种度量方式，并分别以这3种度量方式下风险最小为目标计算了车辆路径。宋伟程等[14]建立了可估算危险品泄漏毒害区面积和损失的评价模型，并结合传统风险模型和最小最大风险模型进行验证。Toumazis等[15]采用条件风险价值理论（CVaR，conditional value-at-risk）构建了基于CVaR的危险品公路运输路径优化模型。曹欢等[16]基于CVaR和公铁联运系统，以风险最小为目标构建了考虑决策者风险规避程度的路径选择模型，证明了决策者的风险规避程度对运输路径和运输方式的选择有重要影响。

3）特殊网络或运输条件。还有一些学者研究特殊网络或特殊运输条件下的问题。Desai等[17]用具有随机分布特征的函数表示人口密度，在随机动态网络上研究了时变条件下的危险品运输路径选择问题。秦军昌等[18]考虑天气状况的影响及决策者的风险偏好，建立了鲁棒优化模型，并将模型线性化以降低求解难度。麻存瑞等[19]研究了不确定环境中考虑决策者风险偏好且鲁棒性可调的路径优化问题，数据分析的结果表明不确定数据间的差异对解的鲁棒性存在影响。辛春林等[20]在时变网络上以费用和风险的加权值最小为目标，建立危险品多式联运的路径选择模型，并提出Dijkstra改进算法进行求解。

单目标危险品运输路径选择各研究的特色与求解方法总结如表3所示。可以看到，这类研究主要以运输风险最小为目标，结合各种不同的实际情形决策危险品运输车辆的路径。对于较为简单的问题，多采用最短路径算法的改进算法或转化为最短路径问题求解;对于较为复杂的问题，则采用各种启发式算法或动态规划的方法求解。由于路径选择问题仅可决策一辆车的路径，这类研究的适用范围较小，可适用于特定场景的车辆路径决策。

1.2 多目标危险品运输路径选择研究

由于研究单目标问题难以体现决策者在风险和成本之间的权衡，学者们展开了对多目标危险品运输路径选择问题的研究，此类问题拥有为数较多的研究成果。不同于单目标危险品运输路径选择研究，多目标问题的优化目标通常需要考虑风险和成本两个方面。Current等[21]较早开始研究此类问题，他们以车辆行驶里程最小和路径覆盖人数最少为目标建立路径选择模型。Zografos等[22]考虑了以承受风险人数最少、事故可能造成的财产损失最小、运输时间最短为目标的路径选择问题，并通过将目标按优先级排序的分层求解法求解。马昌喜等[23]以运输风险最小、运营时间最短及影响敏感人数最少为目标，建立多目标路径选择模型并通过扩展标号法计算出最优折中解。Jassbi等[24]则以运输里程最短、社会风险最小、事故率最小、受影响人数最少为目标进行了研究。殷勇等[25]考虑运输事故级联失效，以事故导致的交通拥堵最小、事故影响的人口最少及运输总费用最少为目标，构建了多目标优化模型。柴获等[26]则以公平性为重点，以风险公平性、多次运输平均成本、多次运输平均风险最优为目标建立了模型。

除上述研究外，学者们还从特殊约束条件、特殊风险度量、特殊网络和特殊运输条件等角度入手，开展了大量研究工作。

1）特殊约束条件。一些学者在问题中加入一系列约束条件，如Meng等[27]建立了考虑有限操作时间及带有等待和服务时间窗约束的双目标危险品运输模型，通过动态规划的方法进行求解。种鹏云等[28]定义了一种危险品运输的连通可靠性，在满足最小路径连通可靠性的条件下建立多目标优化模型，并通过非支配排序遗传算法求解（NSGA-II，non-dominated sorting genetic algorithm-II）。代存杰等[29]根据运输路径的物理特征，设置总风险阈值和最小相异度约束并建立多目标优化模型，数据分析表明危险品运输路径间的相异度约束可减少共用路段/节点数量。

时间窗约束也是学者们的关注点。Androutsopoulos等[30]在客户有时间窗要求的条件下建立以成本和风险最小为目标的危险化学品运输路径选择模型，并采用改进的插入法求解。Verma等[31]研究了以成本和风险最小为目标的公铁联运问题，建立带有软时间窗和惩罚机制的模型并求解，结果表明采用速度更快的列车并选择距离较长但风险较低的路线较为有效。魏航等[32]建立了时变条件下有软、硬宵禁限制的有害品运输最短路径模型，利用动态规划设计算法并證明了算法的复杂性。

2）特殊风险度量。在多目标危险品运输路径选择中，也有学者研究特殊风险度量下的问题。邹宗峰等[33]提出风险指标体系，通过熵权法得出危险品的运输风险，建立路径选择模型并求解。Bronfman等[34]设定人口中心至运输路径的最近距离为安全系数，构建了安全系数最大和成本最小的双目标优化模型。薛翔等[35]将人口中心到附近路段的最短距离与人口中心人数的比值设为道路安全指数，构建了以道路安全指数、总运输成本最优为目标的随机优化模型。

3）特殊网络。大多数研究均基于一般网络，而一些学者则结合特殊网络开展研究工作。例如魏航等[36]在时变网络条件下，以有害品的运输风险和成本最小为目标，研究允许车辆在网络中等待的路径选择问题，算例测试表明等待可以一定程度上减少成本和降低风险。Erkut等[37]则在无管制模型、过度管制模型、两步模型、双层模型这4种不同的网络中以风险最小和成本最小为双目标研究了危险品运输路径选择问题。

危险品运输网络具有明显的双层特征，引起了一些学者的关注。储庆中等[38]以政府期望的风险最小为上层目标，以运输者期望的成本最小为下层目标进行了研究。Minciardi等[39]考虑双层网络条件下上层决策者可通过调整通行费等影响下层决策者，以成本最小和风险最小为目标建立了危险品运输路径选择模型。辛春林等[40]构建一个具有鲁棒性的双层规划模型，并结合Dijkstra算法设计了启发式算法求解。王伟等[41]基于对车辆限速的方法构建模型，上层规划以网络总风险和总时间成本的加权最小为目标，下层规划以危险品运输的总时间成本最小为目标，此后采用粒子群算法求解。

4）特殊运输条件。结合危险品运输的实际情形，学者们在特殊运输条件下进行了研究。多式联运条件下的研究是主要内容，如Verma等[42]研究了危险品公铁联运的双目标路径选择问题。黄丽霞等[43]则研究考虑多批货物且带有送达时间要求的危险货物多式联运问题。还有学者考虑了一些不确定性条件的影响，如刘亿鑫等[44]考虑危险品终端需求量和人口中心的不确定性，构建双重不确定条件下的随机优化模型并求解，结果表明不同样本规模和不确定性条件均会对路径规划产生影响。

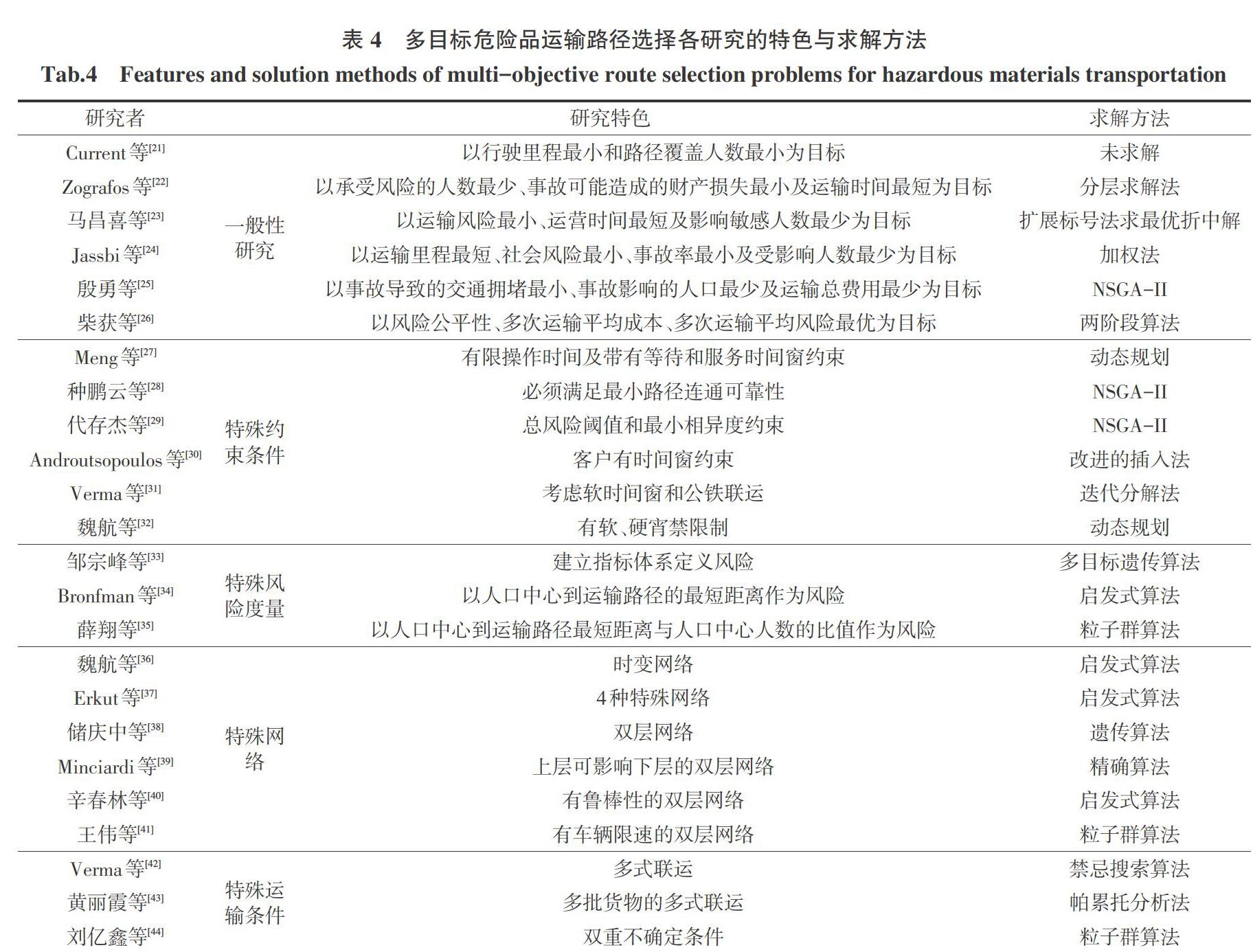
多目标危险品运输路径选择各研究的特色与求解方法总结如表4所示。这类研究主要有两种形式，其一，从反映风险的多个角度提出多个风险目标，并结合成本（或时间/里程等）最小化的目标决策危险品运输车辆的路径;其二，以运输成本和运输风险（主要是期望风险）最小为目标，结合各种不同的实际情形进行车辆路径决策。与单目标优化问题有所不同，求解多目标优化问题的重点和难点在于多个优化目标的处理。从表4可以看到，求解多目标问题的方法多种多样，其中各类多目标进化算法是使用最多的求解方法;这得益于多目标进化算法的适用性较强，易于解决复杂的多目标优化问题，但与此同时也较难在求解方法上做出理论贡献。与单目标危险品运输路径选择研究类似，多目标的研究仍仅可决策一辆车的路径，因此适用范围也较小。

2 危险品运输车辆路径问题研究现状

上文综述的危险品运输路径选择研究主要针对O-D点对间的路径进行优化，然而决策者常需安排整个车队的运输路线，结合危险品运输和车辆路径问题的研究可解决这一问题。对车辆路径问题的研究始于1959年，至今已经历了长足的发展，但对危险品运输车辆路径问题的研究则在进入21世纪后才逐渐成为热点。以下将详细综述这些研究成果。

2.1 单目标危险品运输车辆路径问题研究

类似于单目标危险品运输路径选择问题，单目标危险品运输车辆路径问题也主要是在一般车辆路径问题的基础上考虑与风险相关的特殊优化目标或约束条件。

Tarantilis等[45]研究了多品种的危险品运输问题，他们设定了风险阈值约束，并要求满足风险阈值条件下的运输距离最短。吕品[46]则研究了一个以风险和成本的加权最小为目标的车辆路径问题，并通过遗传算法求解。Bula等[47]基于传统风险的定义，在事故概率中考虑危险品类型和数量的影响，建立了以风险最小为目标的模型并采用遗传算法求解。Bula等[48]进一步针对此问题设计了一个非线性的风险函数，建立模型并设计了一种变邻域搜索算法进行求解。

单目标危险品运输车辆路径问题各研究的特色与求解方法总结如表5所示。这类结合危险品运输和车辆路径问题的研究开始较晚，此时研究多目标的问题已成为学者们关注的重点。因此单目标危险品运输车辆路径问题的研究数量较少，但为多目标危险品运输车辆路径问题的研究奠定了基础。

2.2 多目标危险品运输车辆路径问题研究

多目标危险品运输车辆路径问题可体现风险和成本之间的权衡，虽然问题复杂度比较高，但由于其更为贴近实际的优势，在2010年前后这类问题成为主要的研究方向。较早的成果是Zografos等[49]研究的以运输成本和风险最小为双目标的危险品运输车辆路径问题。柴获等[50]简化了风险因素的量化过程，以车辆数最少、运输总距离及途经人口密集区距离最短为目标建立模型，并设计基于概率模型的多目标进化算法求解。袁文燕等[51]以运输费用和安全风险最小为双目标建立模型，引入描述需求点访问次序的决策变量，减少了传统模型的决策变量个数和约束条件数量。强永等[52]以利润最大化和风险成本最小化为目标构建混合整数规划模型，并通过分层求解法求解。学者们从特殊约束条件、特殊风险度量、特殊网络等角度入手进行研究。

1）特殊约束条件。一些学者在研究中加入了对时间窗的考量，如Pradhananga等[53]建立了带时间窗的危险品运输双目标优化模型，并设计了可求得近似帕累托最优解的启发式算法。Fan等[54]综合考虑危险品运输行驶路段的禁行管控措施，构建了时间窗的保证风险和成本最小化的双目标混合整数规划模型。

还有学者從运输安全性的角度提出特殊的约束条件，例如Wang等[55]在双目标危险品运输车辆路径问题中加入了禁止车辆并行的约束，避免运输过程中出现连环事故的情况。柴获等[56]分析了车辆发生事故与时空距离的关系，以运输成本、风险、运输时间这3者最优为目标，建立了满足时空相异约束的车辆调度模型。

2）特殊风险度量。一些学者们致力于在研究中结合更贴近实际的风险度量。Pradhananga等[57]在风险度量上采用人口暴露模型，建立了双目标优化模型并设计蚁群算法求解。Wang等[55]考虑车辆的个体风险，以车辆个体风险最小和运输成本最小为双目标进行研究，避免总风险不高但某辆车风险特别高的不利情形。Zhang等[58]给出了基于车辆实时装载量的风险定义，以车辆个体风险和成本最小为目标建立风险基于实时装载量的车辆路径优化模型，并基于ε约束法设计了求解算法。张萌等[59]基于重大事故规避的思想，建立了以最大事故后果最小及成本最小为双目标的优化模型。

3）特殊网络。Androutsopoulos等[60]建立了时变网络上以运输成本和总风险最小为双目标的车辆路径模型，采用加权法将原多目标问题转化为单目标问题并设计相应的启发式算法，通过变化权重的值进行多次求解得到近似的帕累托前沿。

对多目标危险品运输车辆路径问题的研究历经了10余年的发展，虽然在成果数量上少于路径选择问题，但其更贴近决策者所面临的实际问题。将多目标危险品运输车辆路径问题各研究的特色与求解方法总结如表6所示。此类研究大多数以运输成本和运输风险最小为双目标，结合各种不同的实际情形进行车辆路径决策。在求解方法上，除传统的加权法和分层求解法、几种常用的多目标进化算法之外，ε约束法依靠其可求得完整的帕累托前沿的优势，得到了越来越多的关注。

3 值得进一步深入研究的方向

学者们针对危险品运输车辆路径优化问题进行了大量研究工作，上文已对现有研究进行了整理和分类。总结各类危险品运输车辆路径优化研究的优点和缺点如表7所示，其中单目标各研究的主要缺点是难以体现成本和风险之间的權衡，路径选择研究的主要缺点是仅可决策一辆车的运输路径，但车辆路径问题求解难度相对较大。伴随多目标问题、车辆路径问题求解技术的发展，研究多目标危险品运输车辆路径问题是未来的主要趋势[61]。总的来说，危险品运输车辆路径优化至今仍保持着一定热度和良好的发展趋势，现有研究存在诸多可改进和完善的空间，也有很多新的问题尚待解决。

第一，在风险度量方面，Erkut等已总结了8种风险度量方式，其中传统风险的使用率最高[2]。但结合传统风险之外的其他度量方式所进行的研究较少，并且这些常见的风险度量主要是对事故率和事故后果的考量，与现实中的情况仍存在距离。未来研究可更深入地探索贴近实际的风险度量，更多地结合多样化的风险度量研究危险品运输车辆路径优化问题。

第二，现有研究中少有细化所运输危险品的工作。危险品的种类多样，各品种危险品具有不同的危险特性和事故后果，例如有毒气体在事故后可能发生泄漏和扩散、易燃液体易行成流淌火导致事故后果扩大。虽已有部分研究考虑了特定品种危险品的特性，但此类研究数量较少，所涉及的危险品种类也有限。如何细分各类危险品，并结合各自的特性对危险品运输车辆路径优化进行研究是未来的关注点之一。

第三，现有研究中尚缺少结合网络拓扑结构所进行的研究。网络包含一般网络、方格式网络、环形放射式网络等多种各具特色的拓扑结构，尤其在城市内进行运输时，网络的拓扑结构是一个需要考虑的重点。例如西安市的路网是典型的方格式网络、上海市的路网则具有环形放射式的特点。在不同结构的网络中进行运输必然会存在不同的特殊性，这些特性会对危险品运输产生何种影响仍亟待解决。

第四，动态网络或动态需求环境下的车辆路径优化问题是近十多年的研究热点之一，但结合危险品运输的研究数量仍然很少。现有动态环境下的危险品运输车辆路径优化研究主要是在时变网络下的研究工作，例如文献[20，36，60]。探求更贴合实际的动态网络和动态需求的定义，并在动态环境下对危险品运输车辆路径优化进行研究，是一个主要的研究方向。

第五，网联车作为未来智能交通的重要组成部分，近年来吸引了许多企业和学者的关注。随着网联车技术的发展，危险品运输将不可避免的涉及网联车领域。如何将危险品运输与网联车等先进技术相结合，是未来发展的一个方向。

第六，目前的研究均认为运输的参与者（如车辆驾驶员）是完全理性人，但现实情况并非如此理想。在假定运输参与者为不完全理性的条件下对危险品运输车辆路径优化进行研究也是一个重要方向。

最后，多目标危险品运输车辆路径优化是未来研究的主要趋势，但现有研究中对多目标问题的求解仍需进一步完善。目前采用的方法多为加权法、分层求解法、多目标进化算法（如NSGA-II）、ε约束法等等。但是这些方法均存在缺陷，例如加权法面临权重选取的困境，分层求解法无法体现各目标间的权衡，进化算法无法求得完整的帕累托前沿;ε约束法可求得完整的帕累托前沿，具有一定优势，但该方法求解大规模问题压力较大，需结合问题性质设计有效的优化策略。如何对这些方法进行改进，或选用更有效的方法，更好地求解多目标危险品运输车辆路径优化问题仍需进一步工作。

4 结语

危险品运输是社会关注的热点之一，危险品运输车辆路径优化也是重要的研究问题。现有研究成果主要集中于危险品运输路径选择问题和危险品运输车辆路径问题两大类，学者们根据研究的需要和现实问题的特殊性将一般车辆路径优化问题的优化目标改为对运输风险的考量，或是同时考虑运输成本最小和运输风险最小进行多目标问题的研究。各类研究有各自的优缺点和适用范围，单目标问题研究的主要缺点是难以体现成本和风险之间的权衡，路径选择研究的主要缺点是仅可决策一辆车的运输路径，但车辆路径问题求解难度相对较大。现有研究存在诸多可改进和完善的空间，未来研究的重点包括：从结合多样的风险度量方式、细分所运输危险品的品种和特性、考虑运输网路的拓扑结构、基于动态网络或动态需求、结合网联车等先进技术、运输参与者为不完全理性的条件等角度对危险品运输车辆路径优化进行研究;建立更贴合实际的模型，选取或开发更好的求解多目标优化问题的方法，得到更具操作性、更贴合现实的危险品运输车辆路径方案，为政府管理部门和危险品物流企业的决策提供理论依据。

参考文献：

[1]    高艳. 我国危化品物流需求强劲[Z]. 中国化工报，2018-1-30（7B）.

[2]    ERKUT E，INGOLFSSON A. Transport risk models for hazardous materials：revisited[J]. Operations Research Letters，2005，33（1）：81-89.

[3]    ALP E. Risk-based transportation planning practice：overall methodology and A case example[J]. INFOR：Information Systems and Operational Research，1995，33（1）：4-19.

[4]    REVELLE C，COHON J，SHOBRYS D. Simultaneous siting and routing in the disposal of hazardous wastes[J]. Transportation Science，1991，25（2）：138-145.

[5]    SACCOMANNO F F，CHAN A. Economic evaluation of routing strategies for hazardous road shipments[J]. Transportation Research Record，1985，1020：12-18.

[6]    ABKOWITZ M，LEPOFSKY M，CHENG P. Selecting criteria for designating hazardous materials highway routes[J]. Transportation Research Record，1992，1333：30-35.

[7]    ERKUT E，INGOLFSSON A. Catastrophe avoidance models for hazardous materials route planning[J]. Transportation Science，2000，34（2）：165-179.

[8]    SIVAKUMAR R A，BATTA R，KARWAN M H. A network-based model for transporting extremely hazardous materials[J]. Operations Research Letters，1993，13（2）：85-93.

[9]    BATTA R，CHIU S S. Optimal obnoxious paths on a network：transportation of hazardous materials[J]. Operations Research，1988，36（1）：84-92.

[10]  DADKAR Y，JONES D，NOZICK L. Identifying geographically diverse routes for the transportation of hazardous materials[J]. Transportation Research Part E：Logistics and Transportation Review，2008，44（3）：333-349.

[11]  何正文，賈涛，徐渝. 基于禁止时间窗的应急物资调度车辆路径问题[J]. 运筹与管理，2009，18（2）：1-6.

[12]  代文强，黄铮. 有害危险废弃物运输网络优化选线模型研究[J]. 运筹与管理，2010，19（6）：134-138.

[13]  KANG Y Y，BATTA R，KWON C. Generalized route planning model for hazardous material transportation with VaR and equity considerations[J]. Computers & Operations Research，2014，43：237-247.

[14]  宋伟程，帅斌，陈钢铁. 基于点危险源的危险品运输路径优化研究[J]. 中国安全科学学报，2012，22（2）：116-121.

[15]  TOUMAZIS I，KWON C. Routing hazardous materials on time-dependent networks using conditional value-at-risk[J]. Transportation Research Part C：Emerging Technologies，2013，37：73-92.

[16]  曹欢，范体军，刘丽萍. 基于CVaR的危险品公铁联运路径选择研究[J]. 运筹与管理，2017，26（6）：41-48.

[17]  DESAI S，LIM G J. Solution time reduction techniques of a stochastic dynamic programming approach for hazardous material route selection problem[J]. Computers & Industrial Engineering，2013，65（4）：634-645.

[18]  秦军昌，张金梁，王刊良. 危险品运输线路问题的鲁棒优化模型[J]. 统计与决策，2009（20）：25-26.

[19]  麻存瑞，马昌喜. 不确定环境中危险品运输路径鲁棒优化[J]. 中国安全科学学报，2014，24（3）：91-96.

[20]  辛春林，冯倩茹，张建文. 时变条件下多式联运危险品路径优化研究[J]. 中国安全科学学報，2016，26（6）：104-110.

[21]  CURRENT J，REVELLE C，COHON J. The minimum-covering/shortest-path problem[J]. Decision Sciences，1988，19（3）：490-503.

[22]  ZOGRAFOS K G，DAVIS C F. Multi-objective programming approach for routing hazardous materials[J]. Journal of Transportation Engineering，1989，115（6）：661-673.

[23]  马昌喜，广晓平，吴芳，等. 发达运输网络环境下危险品公路运输路径决策[J]. 交通运输系统工程与信息，2009，9（4）：134-139.

[24]  JASSBI J，MAKVANDI P. Route selection based on soft MODM framework in transportation of hazardous materials[J]. Applied Mathematical Sciences，2010，4（63）：3121-3132.

[25]  殷勇，刘杰. 关于危险品运输安全性路径选择仿真研究[J]. 计算机仿真，2017，34（8）：184-189，259.

[26]  柴获，何瑞春，马昌喜，等. 考虑风险公平的危险品运输车辆调度优化[J]. 上海交通大学学报，2017，51（7）：855-862.

[27]  MENG Q，LEE D H，CHEU R L. Multiobjective vehicle routing and scheduling problem with time window constraints in hazardous material transportation[J]. Journal of Transportation Engineering，2005，131（9）：699-707.

[28]  种鹏云，帅斌，尹惠，等. 基于连通可靠性的危险品运输路径选择问题[J]. 中国安全科学学报，2014，24（5）：92-97.

[29]  代存杰，李引珍，马昌喜，等. 考虑风险分布特征的危险品运输路径优化[J]. 中国公路学报，2018，31（4）：330-342.

[30]  ANDROUTSOPOULOS K N，ZOGRAFOS K G. Solving the bicriterion routing and scheduling problem for hazardous materials distribution[J]. Transportation Research Part C：Emerging Technologies，2010，18（5）：713-726.

[31]  VERMA M，VERTER V. A lead-time based approach for planning rail-truck intermodal transportation of dangerous goods[J]. European Journal of Operational Research，2010，202（3）：696-706.

[32]  魏航，李军，魏洁. 时变条件下有宵禁限制的有害物品运输最短路研究[J]. 管理工程学报，2007，21（3）：79-85.

[33]  邹宗峰，张保全. 带混合时间窗的多目标危险化学品运输路径优化[J]. 中国安全科学学报，2012，22（4）：83-89.

[34]  BRONFMAN A，MARIANOV V，PAREDES-BELMAR G，et al. The maximin HAZMAT routing problem[J]. European Journal of Operational Research，2015，241（1）：15-27.

[35]  薛翔，朱小林. 不确定需求下危险品运输路径问题的多目标优化[J]. 中国安全科学学报，2016，26（11）：93-98.

[36]  魏航，李军，蒲云. 时变条件下有害物品运输的路径问题研究[J]. 系统工程理论与实践，2006，26（10）：107-112.

[37]  ERKUT E，GZARA F. Solving the hazmat transport network design problem[J]. Computers & Operations Research，2008，35（7）：2234-2247.

[38]  储庆中，张家应，谢之权. 基于双层规划的危险品道路运输网络设计[J]. 重庆交通大学学报（自然科学版），2010，29（4）：597-603.

[39]  MINCIARDI R，ROBBA M. A bi-level approach for the decentralized optimal control of dangerous goods fleets flowing through a tunnel[J]. IFAC Proceedings Volumes，2011，44（1）：9788-9793.

[40]  辛春林，张建文，张艳东. 基于最小最大准则的危险品运输网络优化研究[J]. 中国安全科学学报，2016，26（8）：84-89.

[41]  王伟，张宏刚，丁黎黎，等. 基于车辆限速的危险品运输网络优化研究[J]. 安全与环境学报，2018，18（6）：2091-2095.

[42]  VERMA M，VERTER V，ZUFFEREY N. A bi-objective model for planning and managing rail-truck intermodal transportation of hazardous materials[J]. Transportation Research Part E：Logistics and Transportation Review，2012，48（1）：132-149.

[43]  黄丽霞，帅斌. 危险货物多式联运路径优化问题的多目标优化算法[J]. 中国安全生产科学技术，2014，10（9）：10-16.

[44]  刘亿鑫，朱小林. 双重不确定条件下危险品运输的多目标优化[J]. 计算机集成制造系统，2020，26（4）：1130-1141.

[45]  TARANTILIS C，KIRANOUDIS C T. Using the vehicle routing problem for the transportation of hazardous materials[J]. Operational Research，2001，1（1）：67-78.

[46]  吕品. 基于改进VRP模型的危险品配送路径优化及其求解研究[J]. 中国安全生产科学技术，2011，7（11）：87-91.

[47]  BULA G A，GONZALEZ F A，PRODHON C，et al. Mixed integer linear programming model for vehicle routing problem for hazardous materials transportation[J]. IFAC-PapersOnLine，2016，49（12）：538-543.

[48]  BULA G A，PRODHON C，GONZALEZ F A，et al. Variable neighborhood search to solve the vehicle routing problem for hazardous materials transportation[J]. Journal of Hazardous Materials，2017，324：472-480.

[49]  ZOGRAFOS K G，ANDROUTSOPOULOS K N. A heuristic algorithm for solving hazardous materials distribution problems[J]. European Journal of Operational Research，2004，152（2）：507-519.

[50]  柴獲，何瑞春，马昌喜，等. 危险品运输车辆路径问题的多目标优化[J]. 中国安全科学学报，2015，25（10）：84-90.

[51]  袁文燕，王健，吴军，等. 危险化学品车辆路径问题的一个新模型及算法研究[J]. 系统科学与数学，2017，37（2）：393-406.

[52]  强永，牟瑞芳. 考虑车辆限载的危险品运输车辆调度模型[J]. 系统工程理论与实践，2017，37（1）：212-218.

[53]  PRADHANANGA R，TANIGUCHI E，YAMADA T，et al. Bi-objective decision support system for routing and scheduling of hazardous materials[J]. Socio-Economic Planning Sciences，2014，48（2）：135-148.

[54]  FAN T J，CHIANG W C，RUSSELL R. Modeling urban hazmat transportation with road closure consideration[J]. Transportation Research Part D：Transport and Environment，2015，35：104-115.

[55]  WANG N M，ZHANG M，CHE A，et al. Bi-objective vehicle routing for hazardous materials transportation with No vehicles travelling in echelon[J]. IEEE Transactions on Intelligent Transportation Systems，2018，19（6）：1867-1879.

[56]  柴获，何瑞春，代存杰，等. 考虑时空相异的危险品运输车辆安全调度[J]. 交通运输工程学报，2019，19（3）：145-156.

[57]  PRADHANANGA R，TANIGUCHI E，YAMADA T. Ant colony system based routing and scheduling for hazardous material transportation[J]. Procedia - Social and Behavioral Sciences，2010，2（3）：6097-6108.

[58]  ZHANG M，WANG N M，HE Z W，et al. Bi-objective vehicle routing for hazardous materials transportation with actual load dependent risks and considering the risk of each vehicle[J]. IEEE Transactions on Engineering Management，2019，66（3）：429-442.

[59]  张萌，王能民. 重大事故规避的危险品运输车辆路径优化研究[J]. 运筹与管理，2018，27（8）：1-9.

[60]  ANDROUTSOPOULOS K N，ZOGRAFOS K G. A bi-objective time-dependent vehicle routing and scheduling problem for hazardous materials distribution[J]. EURO Journal on Transportation and Logistics，2012，1（1/2）：157-183.

[61]  张萌，王能民，何正文. 危险品运输车辆路径优化：理论与方法[M]. 北京：清华大学出版社，2020.