装配式预应力组合梁多参数有限元分析
李振华 朱广


作者简介:
李振华(1986—),工程师,硕士,主要从事公路、市政桥涵工程设计工作。
装配式组合结构桥梁在施工以及受力特性等方面具有独特优势。文章针对装配式组合梁的研究现状进行综述,选取预应力度、界面连接强度、预应力施加顺序等参数,基于ABAQUS有限元软件,建立考虑不同参数的有限元模型,对组合梁的承载力以及挠度计算结果进行分析研究,进一步量化分析这些参数对连续梁桥承载力的影响,并基于有限元模型计算结果得到了对应的经验公式,可以应用于指导同类装配式预应力组合梁结构设计。
装配式桥梁;预应力组合梁;多参数分析;ABAQUS
U448.21+6A441556
0 引言
近年来,随着人们环保意识的逐渐增强,桥梁施工对环境造成的影响引起了越来越多的关注。因此,桥梁预制拼装施工技术由于对环境影响较小而得以迅猛发展[1]。此外,采用预制节段拼装施工的桥梁还具有加快施工速度、保证施工进度、减少交通中断的优势。钢-混凝土组合结构因其装配化施工程度高,能够充分发挥混凝土抗压强度高以及钢材抗拉强度高的优点得到越来越广泛的应用[2]。考虑到结构的稳定和抗扭等,钢梁截面常取为箱梁形式[3]。钢箱与混凝土之间的界面粘结作用以及剪力键是保证两种材料共同工作的基础,工程上一般采用在界面设置足够多的抗剪连接件的方法来保证型钢和混凝土的共同工作。但是在界面设置过多的剪力键会造成施工难度及施工成本的增加,因此应考虑设置合适的连接强度[4]。栓钉剪力键是工程中应用最为广泛的一种剪力键,本文以设置了该类型连接件的装配式组合梁为例进行参数化分析[5]。随着桥梁跨径的增加,预应力钢-混凝土组合梁结构和预应力钢-混凝土连续组合梁结构应运而生[6],预应力结构的出现解决了普通钢-混凝土组合梁负弯矩区易开裂和刚度普遍较低的难题。目前,连续组合梁负弯矩区的抗弯性能研究并不充分。《钢结构设计规范》(GB50017-2003)中采用了折减刚度法来考虑组合梁的刚度折减[7]。以该方法计算结果可能会出现抗弯刚度随着抗剪连接程度的增大而减小的异常现象。主要原因是该方法忽略了大跨组合梁桥在偏载作用下的空间效应。且相关研究表明:同一截面内的挠度及界面滑移的分布也是不均匀的,因此规范计算方法在大跨组合梁桥的应用中具有局限性。
ABAQUS是一种大型通用有限元计算分析软件,能够求解复杂的接触问题和高度非线性问题[8]。本文采用ABAQUS软件建立装配式预应力组合梁的有限元模型,并借助MATLAB软件对有限元计算结果进行参数化分析,得到了实用的计算公式[9],为装配式组合梁的承载力及极限挠度计算分析提供参考。
1 研究参数的选取
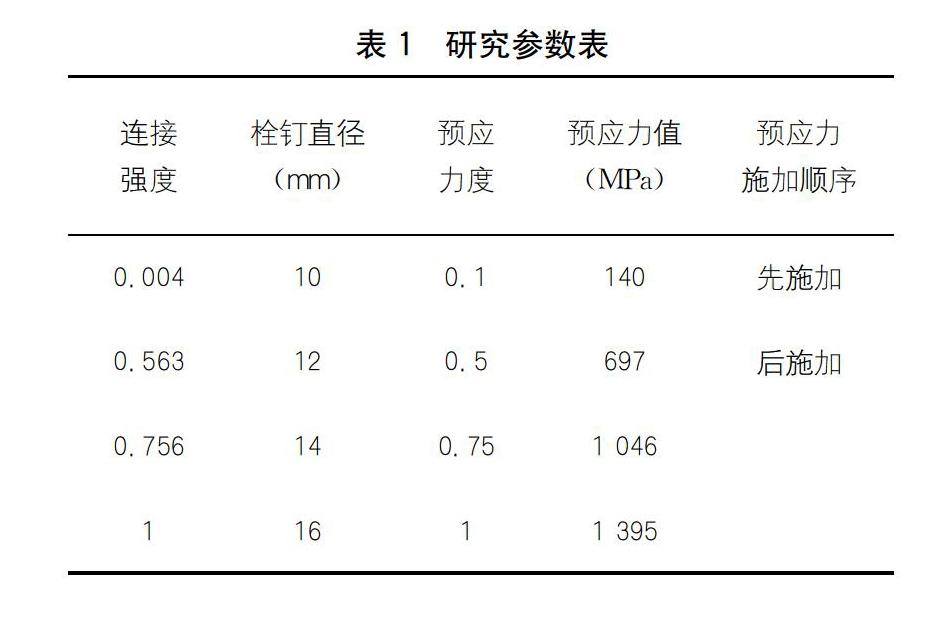
研究表明,影响装配式连续组合结构抗剪滑移性能的因素很多,抗剪滑移性能将直接影响组合结构的承载力[10]。参考相关研究成果,本文分别选取预应力度、预应力施加顺序、界面连接强度等三个参数进行有限元分析。本文采用栓钉面积与最大直径栓钉(16 mm)面积之比表征组合截面的连接强度,共选取0.001、0.563、0.756、1四种类型的连接强度。通过调节预应力度(用预应力值与最大预应力比值表征),可以进行负弯矩区混凝土的抗裂和裂缝宽度控制。本文共选取0.1、0.5、0.75、1四种类型的预应力度进行研究,对应的预应力值分别为140 MPa、697 MPa、1 046 MPa、1 395 MPa。此外,预应力的施加顺序对配有预应力筋的连续组合梁的力学性能影响很大。如果在浇筑剪力槽之前施加预应力,预应力荷载不会通过剪力槽传递给钢箱,所施加的预应力会全部作用在混凝土板上,可以提高预应力的作用效果;如果在采用后张预应力的方法,能够提高组合梁的整体连接性能,因此有必要综合考虑预应力的施加顺序。
将本文采用的主要研究参数列于表1。
2 工程背景
选取某两跨连续组合钢箱梁桥为工程背景,桥跨立面布置如图1所示,横断面细部尺寸如图2所示。混凝土桥面板共配置4根预应力钢筋,直径为15.2 mm,板顶底面共配置两层钢筋网片,钢筋间距为150 mm,钢筋直径统一为16 mm,钢箱梁板厚统一为10 mm。
3 有限元模型建立
3.1 材料参数
对于混凝土材料,采用混凝土塑性损伤本构。塑性损伤能够代表混凝土材料在受力过程中的非彈性行为,是一种基于各向同性弹性损伤和各向同性的拉伸和压缩形式的塑性混凝土的非线性行为的结合。其塑性应力应变关系如图3所示。对于钢材,统一选用理想弹塑性本构。其应力应变关系如图4所示。
混凝土采用三维实体单元(C3D8R)进行模拟,钢筋采用三维桁架单元。为简化计算,本文建立1/4全桥模型,见图5。
3.2 边界条件及加载方式
模型采用对称约束。为模拟原桥负弯矩区的受力情况,采用跨中自下而上的加载方式,为保证计算的收敛性采用了位移的加载方式。板内钢筋采用嵌入约束的方法,对预应力采用降温法,即对混凝土板内预应力钢筋降温从而将预应力荷载施加到混凝土板上。钢箱与混凝土界面采用硬接触约束,考虑组合截面的相对滑移。
4 计算结果
选取编号为M1的模型有限元计算结果为例,下页图6给出各个部件对应的应力及挠度计算结果。
由图6可知,组合梁M1在极限状态下,混凝土板内普通钢筋在跨中位置发生屈服,而预应力钢筋未达到屈服。此时栓钉跨中部分屈服,端部栓钉全部达到屈服应力500 MPa,表明组合梁界面相对滑移呈“两端大中间小”的趋势。由图7可知,组合梁跨中挠度为42 mm,极限承载力为Pu=828×4=3 311 kN。
将各模型的挠度及对应的承载力计算结果列于表3。
利用Matlab软件对上述结果的相关性进行计算。计算过程如下:
由计算结果可知,连接强度跟组合梁的极限挠度和极限承载力的相关系数分别为-0.988 5和0.906 9,表明两者相关性较大。连接强度与极限挠度的关系如图8所示,连接强度与极限承载力的关系如图9所示。
由图8可知,极限挠度随着连接强度的增加而减小,最大与最小挠度的差异在35%左右,表明极限挠度对连接强度较为敏感。由图9可知,极限承载力随着连接强度的增加而增大,增大幅度在8%左右,具有一定的工程意義,而预应力度对组合结构的极限承载力影响不大。
当结构的连接强度为1时,极限挠度和极限承载力随着预应力度的变化情况如图10所示。
由图10(a)可知,当预应力度<0.75时,预应力连续组合结构梁桥的极限挠度随预应力度的增加而增大,当预应力度>0.75时,极限挠度值反而减小。由图10(b)可知,预应力连续组合结构桥的极限承载力随预应力度的增加而增大,当预应力度<0.75时,极限承载力增长幅度较大。通过两组数据的对比结果可知:预应力的张拉顺序能够提高组合梁的极限承载力,但提高幅度较小。综上,可重点分析连接强度和预应力度对极限挠度和极限承载力的影响。
考虑连接强度和预应力度两个因素,利用Matlab软件分别对极限挠度计算结果和极限承载力结果进行二元二次多项式拟合,得到相应经验公式,拟合结果如图11、图12所示。
故极限挠度拟合结果δmax=f(x,y)=15.99-3.149x-0.631y-2.715x2+0.647xy+0.249y2,拟合优度R方为0.956,满足要求。式中“x”表示界面连接强度,“y”表示预应力度。
极限承载力结果f(x,y)=3 329-231.1x-79.37y+516.8x293.67xy+96.9y2,“x”表示界面连接强度,“y”表示预应力度,拟合优度R方为0.964,表明拟合效果较好,满足工程应用要求。
5 结语
装配式组合结构在施工及设计方面具有一定的优势。本文通过对两跨组合梁的有限元结果进行参数化分析,可得到以下结论:
(1)基于ABAQUS软件的有限元模型计算结果(挠度和承载力)能够反映实际结构的空间受力行为。
(2)根据对有限元结果的相关性分析可知,预应力度、界面连接强度两个参数(跨径及跨数)对组合梁承载力以及极限挠度的影响较为显著,为经验公式的建立提供了依据。
(3)根据参数化分析结果,得到考虑预应力度、界面连接强度两个因素的跨中极限挠度以及极限承载力的经验公式。通过对拟合结果进行拟合优度分析可知,拟合结果和有限元结果吻合较好,该公式可用于指导同类连续组合梁结构设计。
(4)对于有预应力筋的组合梁,在剪力槽浇筑后张拉预应力筋,能够在一定程度上提高组合梁的极限承载力,减小极限挠度,但这种改变幅度较小。
[1]苗冬梅,马昕煦,牛 辉,等.装配式混凝土干式连接结构安装关键技术[J].施工技术,2018(4):35-40.
[2]刘 琼,李向民,许清风.预制装配式混凝土结构研究与应用现状[J].施工技术,2014,43(22):9-14,36.
[3]JGJ1-2014,装配式混凝土结构技术规程[S].
[4]吴安耀.试析公路桥梁施工中的预应力技术[J].西部交通科技,2017(7):90-92.
[5]李成君,周志祥,黄雅意.装配式组合梁剪力钉滑移性能研究[J].公路工程,2017,42(2):111-115.
[6]韩 超,郑毅敏,赵 勇.钢筋套筒灌浆连接技术研究与应用进展[J].施工技术,2013,42(21):113-116.
[7]戴公连,李德键.桥梁结构空间分析设计方法与应用[M].北京:人民交通出版社,2001.
[8]毛昆明,陈国兴.基于ABAQUS软件的并行计算异构集群平台的搭建[J].地震工程与工程振动,2011,31(5):184-189.
[9]郑阿奇,曹 戈.MATLAB实用教程[M].北京:电子工业出版社,2004.
[10]白 玲,史志强,史永吉.剪力键布置方式对连续组合梁桥受力特性的影响[J].中国铁道科学,2003,24(2):67-71.

