“几何概型”教学设计与反思

王晓红

教学内容：人教版高中二年级数学必修3第三章概率第三节几何概型第1课时。

教学目标：

1.通过本节课的教学，让学生理解几何概型的实质性概念;掌握其概率计算公式;能够区分几何概型与古典概型，并能发现他们之间的联系，并能正确识别不同的概率模型。

2.通过问题探究及辨析，形成概念，体验数学概念生成的过程，找到数学的乐趣。通过类比古典概型，推理几何概型问题，并提出解决几何概型问题的想法。

3.通过故事情境，激发学生的学习兴趣，通过学生自主探究、合作交流，初步形成建立数学模型的能力，让学生认识到数学与生活息息相关。

教学重点：

理解几何概型的概念及两个特征，会应用其计算公式。

教学难点：

会判断几何概型类型，无限过渡到有限，建立合理的几何模型求解概率。

教具准备：多媒体课件和几何画板软件等。

教学过程：

一、创设情境，引入课题

探究一：

问题1：在数轴上，从区间[0，9]上任取一个整数，恰好取在区间[2，4]上的概率为多少？

问题2：在数轴上，在区间[0，9]上任取一个实数，恰好取在区间[2，4]上的概率为多少？

探究二：

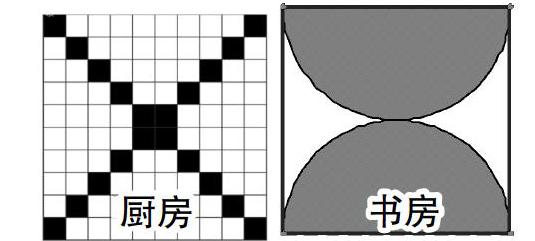
下图是小明家厨房的和书房的地面示意图，厨房每一块方砖除颜色外完全相同，书房的地面轮廓是正方形，灰色部分是以正方形边长为直径做的半圆围成的，一只甲壳虫在厨房和书房中自由地飞来飞去，并随意地停留在地面的任何一个位置上（假设甲壳虫不落在邊界上），请问：

（1）甲壳虫在厨房停留在黑色区域的概率有多大？

（2）甲壳虫在书房停留在灰色区域的概率有多大？

探究三：

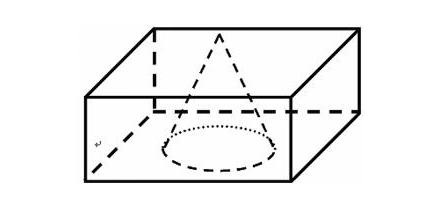
晚上，小明想抓住这只在书房里乱飞的甲壳虫，于是他只打开了屋顶最中间的一个射灯，射灯照明的范围大概是一个圆锥体（如图），底边半径为，忽略书房内陈设可把书房抽象成一个长方体，长宽高依次为a，a，b。设甲壳虫在房间的每一个点都是等可能的，求它飞入射灯照明范围内的概率。

学生主体活动：创设问题情境，探索新的解决办法，让学生给出思路和答案。

设计意图：通过解决问题，回顾古典概型的相关知识，对比问题2形成认知冲突，进而发现新的解决办法。通过对以上3题的探究，发现共性与本质，归纳出概念。

二、归纳总结，知识梳理

1.几何概型的概念。

如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，简称为几何概型。

2.概率计算公式。

3.几何概型的基本特点。

①试验中的基本事件有无限多个;

②每个基本事件出现的可能性相等。

4.古典概型与几何概型的区别。

相同点：基本事件发生的可能性相等。

不同点：古典概型的基本事件是有限个，几何概型的基本事件有无限个。

三、辨析举例，推广应用

例1：

题组一

1， 在一个面积为S的三角形ABC的边AB上任取一点P，求使S△PBC>S的概率。

2， 在一个面积为S的三角形ABC面内任取一点P，求使S△PBC>S的概率。

题组二：

1.在一个体积为V的四棱锥F-ABCD的面FBC上任取一点P，求使得四棱锥P-ABCD的体积VP-ABCD>V的概率。

2.在一个体积为V的四棱锥F-ABCD的体内任取一点P，求使得四棱锥P-ABCD的体积VP-ABCD>V的概率。

题组三：

1.有一个带指针的转盘如图所示，求转动停止后指针在红色区域的概率。当转盘等比例缩小时，这时指针停在红色区域的概率有变化吗？

2.如果将上题的转盘盘面制作成靶子，若某同学向靶子射飞镖，假设一定能中靶，求飞镖落在红色区域的概率。

题组四：

1.等腰Rt△ABC中，∠C=90？紫，在直角边BC上任取一点M，求∠CAM<30？紫的概率。

2.等腰Rt△ABC中，∠C=90？紫，在∠CAB内任意作射线交线段BC于点M，求∠CAM<30？紫的概率。

学生活动，发现不同，深入体会。

设计意图：辨析与长度和面积相关的几何概型;辨析与面积与体积相关的几何概型;辨析与面积与角度与弧长相关的几何概型;辨析与长度与面积相关的几何概型。

例2：

暑假的一天，小明打算坐公交车去动物园，他要乘坐的公交车每隔15分钟有一辆，已知小明任意时刻到达车站，试问小明到达车站候车时间大于10分钟的概率？

设计意图：将实际问题转化为几何概型问题来解决。

思考题：

小明和好友小亮约定在动物园门口见面一起入园游玩，假定两人都在上午10：00-11：00之间随机到达，先到者等另一个人20分钟，过时不等，先到者就自己独自入园，求两人能见面一起入园游玩的概率？

设计意图：由一维到二维，思维难度加大。

四、巩固升华，总结概括

由学生自主回顾本节内容小结一下。然后结合学生的小结，教师做以下总结：

古典几何等可能，

有限无限各不同。

概率即为测度比，

长面体角要分清。

设计意图：借用小诗，加深对本节课基础知识的理解。

反思：

本节课通过问题探究及辨析，形成数学概念，体验数学概念生成的过程;通过类比古典概型，推理几何概型问题，并提出解决几何概型问题想法;通过故事情境，激发学生学习数学的乐趣;通过引导学生动手操作，合理利用随机、统计、化归、属性结合等数学思想方法有效解决有关的概率问题;通过学生自主探究、合作交流，初步形成建立数学模型的能力。我认为本节课的最大亮点是我在问题对比过程中设计的问题很清晰，层层递进，类比转化，学生对概念的辨析透彻。

本节课不足：由于难点是让学生实现有限和无限之间的对应转化，从而解决无限难以计算的问题，在问题设置中我应该加强对引起学生思维困惑后的引导。学生在理解有限与无限的内在对应问题上，逻辑上认识不够清晰，所以应该再细化概念生成过程中的问题，让学生自主探索、合作交流再深入一些效果可能会更好。

编辑/魏继军