向量组等价的新刻画

黄 菊，康碧芳

（闽南师范大学 数学与统计学院，福建 漳州 363000）

矩阵与有限维向量组是一一对应的，且秩是刻画矩阵的不变量之一。曹青春等［1］证明了数域P 上的两个m×n 矩阵A 与B 行（列）等价当且仅当它们的行（列）向量组等价。本文利用向量组等价定义与矩阵的秩刻画向量组等价的新定理，并得到关于向量组等价的一些推论。

定义1［2-3］设向量组A：α1，α2，…，αs与B：β1，β2，…，βt是n 维列向量空间Pn的两个向量组，如果它们能够互相线性表出，则称α1，α2，…，αs与β1，β2，…，βt等价。

向量组A 能由向量组B 线性表示，即存在kij（i=1，2，…，r；j=1，2，…，s），使得

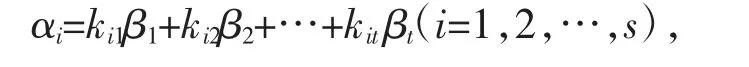
即有

设矩阵K=（kij）t×s，A=（α1，α2，…，αs），B=（β1，β2，…，βt），则A=BK。

类似地，若向量组B 可由向量组A 线性表示，即存在矩阵K'=（t'ij）s×t，使得B=AK'。

定理1 设向量组A：α1，α2，…，αs与向量组B：β1，β2，…，βt是n 维列向量空间Pn的两个向量组。如果向量组A 与B 等价的充分必要条件是存在矩阵K∈Pt×s，K'∈Ps×t，使得A=BK，B=AK'充分必要条件是（rA）=（rA，B）=（rB）。

证明向量组A 与B 等价的充分必要条件是存在矩阵K∈Pt×s，K'∈Ps×t，使得A=BK，B=AK'，其含义即方程AX=B，BY=A 有解的充分必要条件是（rA）=（rA，B）=（rB）。证毕。

推论1 设向量组A 与B 等价。

（1）若（rA）=s，则K'K=Es；

（2）若（rB）=t，则K'K=Et。

证明由定理1 知，存在矩阵K∈Pt×s，K'∈Ps×t，使得A=BK，B=AK'。从而有A=AK'K，即A（Es-K'K）=0，又（rA）=s，从而有K'K=Es。证毕。

推论2 设向量组A：α1，α2，…，αn与向量组B：β1，β2，…，βn是n 维列向量空间Pn的两个向量组，则向量组A与向量组B 等价的充分必要条件是存在可逆矩阵K，使得A=BK。

由向量组等价定义及判断表示矩阵可逆得两个向量组等价，进而两个向量组秩相等。

例 设β1=α2+…+αr，β2=α1+α3+…+αr，…，βr=α1+α2+…+αr-1，证明：向量组β1，β2，…，βr与向量组α1，α2，…，αr有相同的秩。

证明方法一：依题可知，向量组β1，β2，…，βr可由向量组α1，α2，…，αr线性表出。又

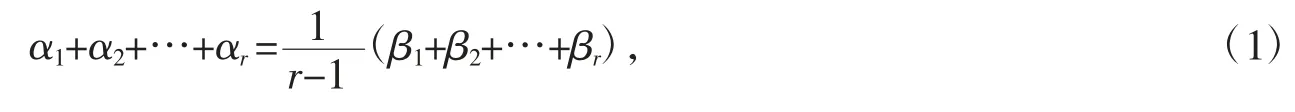
从而有αi=（β1+β2+…+β）r-βi（i=1，2，…，r），故向量组α1，α2，…，αr可由向量组β1，β2，…，βr线性表出，即两个向量组等价，则两个向量组具有相同的秩。

方法二：将题意中向量组表示改成矩阵乘积，即