大型翼伞操纵转弯动力学研究
王国庆 滕海山 王奇
(北京空间机电研究所,北京 100094)
0 引言
相比于传统的圆形降落伞,翼伞以其优越的滑翔性能以及可控性,广泛应用于精确空投以及航天器回收与返回等领域。为了投放大质量载荷,大型翼伞亟待开发。由于翼伞的翼面是柔性结构,翼面越大受到风场的影响也就越大,所以相较于中小型翼伞,对大型翼伞进行精确建模和控制的难度也就更高。随着计算流体动力学(CFD)的发展、空投系统以及航天器回收过程对定点回收精度要求的提高,精确计算大型翼伞的气动参数必不可少。针对升力系数、阻力系数、侧力系数等关键参数的变化进行研究是对大型翼伞准确动力学建模的必要条件。
翼伞通过控制两侧操纵绳来进行转弯,研究翼伞操纵转弯动力学目的就在提升控制精度,使得落点更加精确。翼伞的操纵转弯动力学主要包括气动特性和动力学建模两方面内容。对于翼伞的气动性能研究,国外从20世纪60年代开始经历了从试验到仿真的发展历程[1-8]:文献[9]对不同尺寸的翼伞进行了风洞试验,研究了升力系数、阻力系数等气动参数随迎角的变化,为以后的数值仿真结果验证提供了大量的数据;文献[10]选取改进下表面平直的翼型,研究了单边下拉量对横向运动的影响和双边下拉量对纵向运动状态的影响;文献[11]采用有限体积法求解κ-ε二方程湍流模型下的N-S方程,对翼伞单侧后缘下拉情况下的气动性能进行了初步分析;文献[12]模拟了翼伞在转向与雀降阶段的气动性能,实现了翼伞气动模型的修正;文献[13]采用有限体积元法求解N-S湍流模型的κ-ε控制方程,得到了不同迎角来流条件以及伞衣后缘不同下拉程度的气动力数据。
对于翼伞的动力学模型研究,根据不同的研究重点,选取的自由度也各有不同:文献[14]在四自由度翼伞模型下,利用各轨迹段的几何关系,对目标函数进行参数寻优,进而得到轨迹的设计参数;文献[15]建立六自由度模型并引入襟翼偏转气动模型,对空投翼伞进行动力学建模,为空投翼伞精确建模提供新思路;文献[16]建立了六自由度刚性连接模型,重点分析了翼伞系统的滑翔特性和转弯特性,为翼伞系统在空投上的运用提供了理论支撑;文献[17]采用拉格朗日乘子法建立了两体八自由度和三体十自由度多体动力学仿真模型,研究了不同吊挂方式和不同有效载荷外形气动力对系统滑翔和转弯性能的影响;文献[18-21]分别进行了九自由度动力学建模和仿真,利用动力学仿真软件ADAMS对翼伞空投系统飞行动力学过程进行了计算。
到目前为止,对于翼伞的气动特性计算和建模方法相对完善,但是由于受限于翼伞的研制能力,这些研究都局限于中小型翼伞,未对大型翼伞有过多涉及,也缺少空投试验数据的验证。
本文研究的翼伞是300 m2大型翼伞,对大型翼伞系统的侧力系数进行了多角度的计算和分析,把结果加入到动力学模型当中对大型翼伞系统的转弯运动进行仿真分析,得到了大型翼伞系统的转弯特性,并将仿真数据与试验结果相对比,验证了计算、模型和仿真的合理性,可为大型翼伞的设计提供参考。
1 研究对象
本文分析的翼伞几何参数为:展长27m、弦长11m,展向划分为18个气室,伞衣的前缘部分从正面看为圆弧形状,半径为26m;在后缘距离两侧边缘各9m范围内平均分布8条操纵绳,用于完成大型翼伞转弯运动控制;初始下拉量为0.5m,最大下拉量为2.5m。该大型翼伞系统的设计参数如表1所示。

表1 大型翼伞的设计参数Tab.1 Design parameters of large parafoil
2 侧力系数计算
翼伞系统的翼面是柔性结构,可以通过后缘操纵下拉使其发生形状变化,从而改变受力形式和运动状态,不同程度的下拉量使其发生的形状变化程度也有不同。大型翼伞在后缘单侧下拉时会产生偏航力矩、滚转力矩和侧力,并开始转弯运动,其中侧力也是气动力的一种,是转弯运动向心力的重要组成部分,会随着操纵下拉量的不同而发生变化,对其进行研究的关键即在于对侧力系数的研究。
2.1 理论推导法
大型翼伞后缘操纵绳共有8根,平均分布在翼伞两侧下拉范围内,该下拉范围是两侧向内三分之一展长的区域,操纵绳与伞体夹角σ,翼伞侧视图如图1所示。
大型翼伞后缘操纵绳单侧下拉的长度L和后缘下降高度ΔL之间关系如式(1)所示,将侧视图中的伞衣后缘与操纵绳连接部分局部放大,局部示意如图2所示。其中实线表示伞衣形状,可以看出在下拉情况下,伞衣向下弯曲,从而为伞衣整体受力带来了变化。

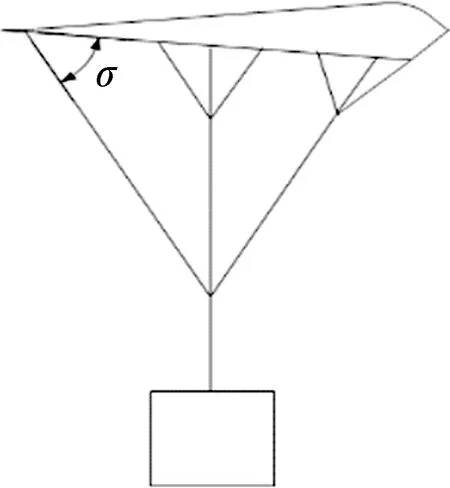
图1 大型翼伞侧视示意Fig.1 Side view of large parafoil
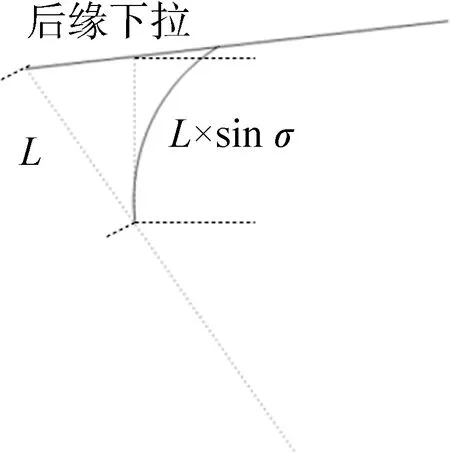
图2 后缘下拉局部示意Fig.2 Local drawing of trailing edge pull down
大型翼伞在未进行操控时,可以将伞面视为一个薄板,在本体坐标系X方向上没有投影面积,后缘单侧下拉L后会产生一个本体坐标系X方向的投影面积S1(如图3所示),其计算公式为

式中b是展长。
由于后缘受拉部分的翼面下偏,在本体坐标系Z方向的投影面积减小ΔS,

下拉之前可以近似认为翼伞在本体坐标系X方向没有投影面积,翼伞阻力来自于翼型的气动特性。而在单侧下拉之后,在X方向出现的投影面积会带来新的一部分阻力FD1,如图4所示。从图4中可以看出,阻力FD1作用点近似认为在S1面积的中心,阻力系数取1,FD1大小为

式中ρ为空气密度;0v为纵向平面内系统的速度。
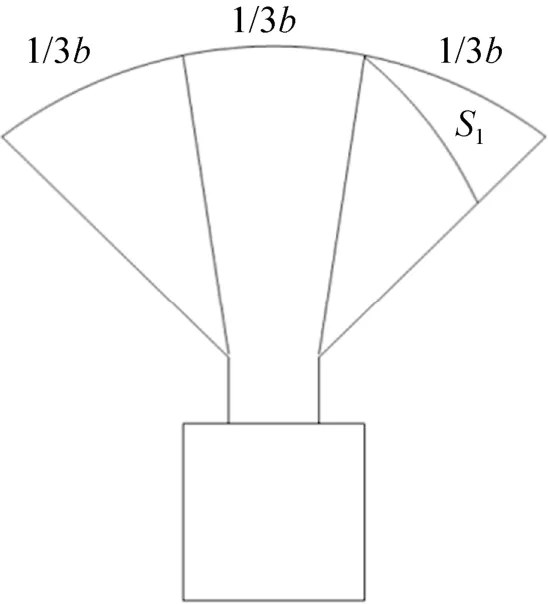
图3 大型翼伞单侧下拉主视图Fig.3 Single pull down main view of large parafoil

图4 大型翼伞单侧下拉俯视受力示意Fig.4 Large parafoil with one side pull down
另外,随着大型翼伞Z方向面积的减少,气动升力和阻力都会有所下降,变化量分别为:

其中,ΔLF为升力下降的变化量;CL为翼伞升力系数;ΔDF为阻力下降的变化量;CD为翼伞阻力系数。
由于阻力FD1只作用在下拉一侧,所以会对大型翼伞系统产生一个偏航力矩MDY,从而出现侧滑角,使得大型翼伞出现侧向气动力,即侧力FY,侧力使大型翼伞做转弯运动。MDY和FY计算如下:

式中S为翼伞原面积;CY是翼伞侧力系数。
大型翼伞系统在偏航力矩MDY的作用下转动时,侧力 YF会产生一个恢复力矩MYY,在力矩的共同作用下,侧滑角逐渐开始增大到保持不变,大型翼伞系统会在偏航方向上达成平衡。这一恢复力矩为

式中LSG为伞衣质心到系统质心的距离;θ为俯仰角。由于翼伞系统在偏航方向达到平衡,其侧向合力矩M侧为0,即

由式(3)~(4),(7)~(10)可以得到:

本文以300m2大型翼伞为例进行研究,将大型翼伞系统设计参数和空投试验数据代入,得到此型大型翼伞系统侧力系数为

式中δ为下拉量的百分比。
2.2 CFD仿真法
由于伞绳很细,阻力较小,翼伞载荷主要考虑伞衣所受的载荷,在CFD仿真时主要分析伞衣的气动特性和表面压强分布,不考虑伞衣透气性的影响。内腔和外部流场划分为非结构网格,入口边界距离翼伞5倍弦长,其余边界距离翼伞10倍弦长。在距离翼伞比较近的区域进行了网格加密,并在边界附近划分了边界层网格,网格数目为3×106。模拟海平面处0°攻角和10°攻角,速度20m/s,翼伞下拉量分别为50%和100%的转弯飞行气动特性,入口为速度入口,出口为自由出口。其他外部边界为自由边界条件,翼伞上下翼面和翼肋为壁面边界,内腔和外部流场通过软件中设定的交换面接口interface交换数据。为了考虑翼肋上开口的影响,将内腔用翼肋划分为18个气室,相邻气室在翼肋开孔处用interface交换数据,湍流模型采用κ-ε二方程模型。翼伞对称截面流场和滑翔过程流线如图5、6所示。
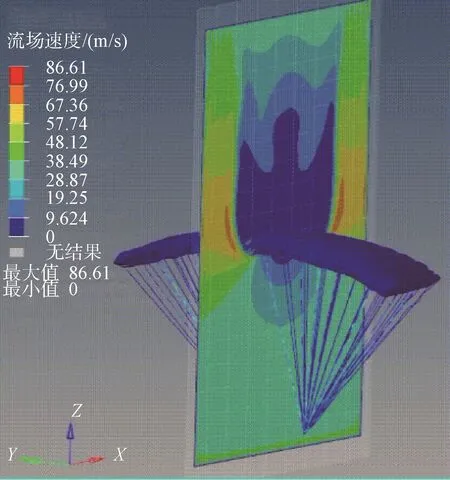
图5 翼伞对称截面流场速度标量云图Fig.5 Symmetrical cross-section flow field
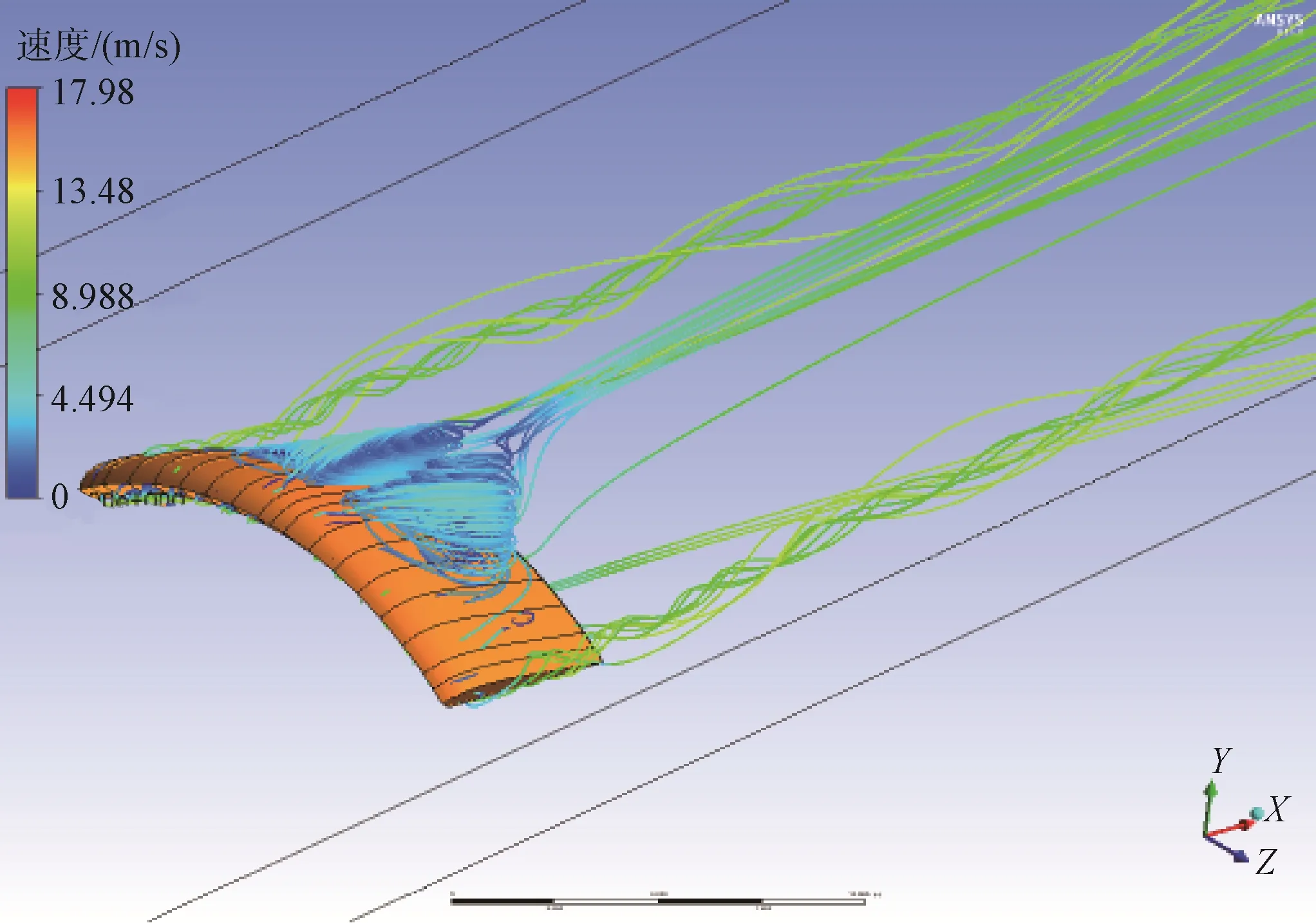
图6 翼伞滑翔过程流线Fig.6 Streamline diagram of gliding process
经过计算,可以得到后缘下拉过程气动数据变化,结果如表2所示。

表2 后缘下拉过程气动数据变化Tab.2 Change of aerodynamic data during trailing edge pull-down process
表2 中,偏航力矩系数Cm的计算公式为

式中c为翼伞弦长;Mz为作用在伞衣上的偏航气动力矩。
偏航力矩系数基本随攻角呈线性变化,在攻角为17°时,下拉量为50%和100%的偏航力矩系数分别为0.001 1和0.001 3。再根据偏航趋势考虑到侧滑角的影响,解得此条件下,在下拉量为1 500mm(即δ=50%)时侧力系数CY为0.025 1;下拉量为2 500mm(即δ=100%)时侧力系数CY为0.053 7。
2.3 空投试验法
侧力 YF的分量作为向心力,使大型翼伞系统做转弯运动,有如下关系成应:

式中m为系统质量;R为转弯半径;β为侧滑角;u为本体坐标系下X方向速度,计算公式为

由式(8),(14)~(15)得:

根据式(16)和大型翼伞空投试验数据来求解出不同工况下的CY值,再经拟合求解出CY与δ的关系。
某架次空投试验中大型翼伞下拉长度变化范围是500~2 500mm,系统质量4 250kg,攻角17°。取其中部分转弯过程数据计算对应侧力系数CY,结果如表3所示。
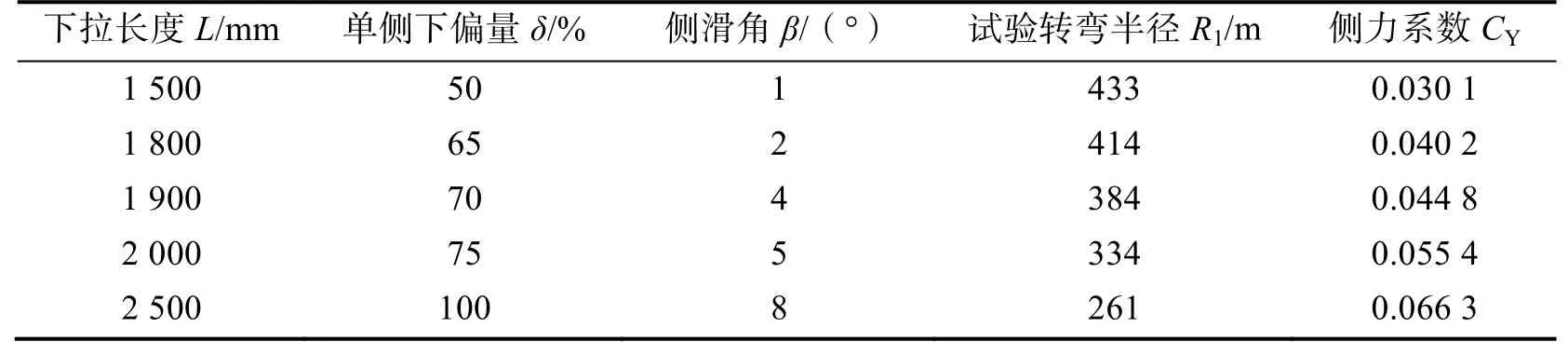
表3 试验转弯数据Tab.3 Test turning data
将3种方法得到的侧力系数相比较,取δ=50%、δ=100%计算得到表4:

表4 不同方法得到侧力系数比较Tab.4 Comparison of lateral force coefficients obtained by different methods
从表4中可以看出,在下拉量100%时试验法算得的侧立系数与理论算法和CFD仿真法的结果有一定偏差,这是由于试验在高空环境,空气密度取值较小造成的。除此之外,系数偏差较小,表明了推导过程的准确性。由于CFD仿真法和试验法得到的侧力系数数据比较离散,所以在下面的建模和仿真工作中,使用2.1中的理论推导法得出的侧力系数公式。
3 动力学建模
本文研究的对象是全展开飞行状态下的大型翼伞,对其建立六自由度模型进行研究。六自由度模型是将整体系统视为刚性体进行分析,其中包括质心的平动和绕质心的转动,这能在一定程度上反应整体的运动状况。
假设地球的重力加速度为常数,忽略地球的哥氏加速度和曲率的影响,伞体与载荷刚性连接成为一个整体,伞衣的压心和重心重合,且升阻系数取为常数,载荷表面积较小,忽略其升阻力。
建立三个坐标系:1)OiXiYiZi大地坐标系,也称作惯性坐标系;2)ObXbYbZb本体坐标系;3)OaXaYaZa气流坐标系。
根据动量定理和动量矩定理,可以得到大型翼伞的运动方程为[23]

式中V为速度矢量;W为角速度矢量;A为质量特性矩阵;Fa为气动力;FG为重力;Fn=-W×P是耦合项,P是动量;Ma为气动力矩;MG为重力矩;Mn=-W×H-V×P是耦合项;H为动量矩;气动力Fa可表示为

式中FL为翼伞升力;FD为翼伞阻力;FDw是载荷阻力。式(18)中FL,FD,FY的计算公式分别为:
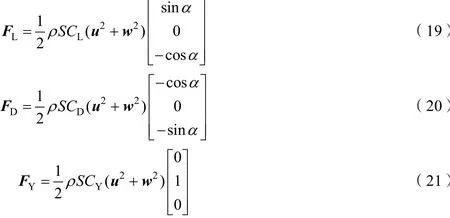
其中,w是本体坐标系下Z方向速度。
对于侧向力矩,在2.1节中已经有过计算,即式(10),对于滚转方向和俯仰方向力矩,用各个力和对应力臂相乘即可得到。
4 仿真分析
在给定初始条件和输入的情况下,在simulink中构建动力学模型,求解该大型翼伞系统的运动情况。
4.1 操纵下拉转弯响应
以操纵绳单侧下拉量100%(最大下拉量)转弯飞行为例,研究体坐标系下三个方向的速度、俯仰角、攻角及地坐标系下水平面轨迹,结果如图7~12所示,其中前50s为无控制自由滑翔。由图7~9可以看出,当右侧操纵绳下拉时,本体坐标系下X方向速度从15m/s增加到22m/s,Y方向速度从0m/s增加到7m/s,Z方向速度稳定后几乎与下拉前无变化。如图10~11,俯仰角和攻角都随着右侧操纵绳下拉而减小,俯仰角减小幅度更大;图12为全运动过程的水平面轨迹,可以看出整个运动过程大型翼伞系统在右侧操纵绳下拉之后螺旋下降。
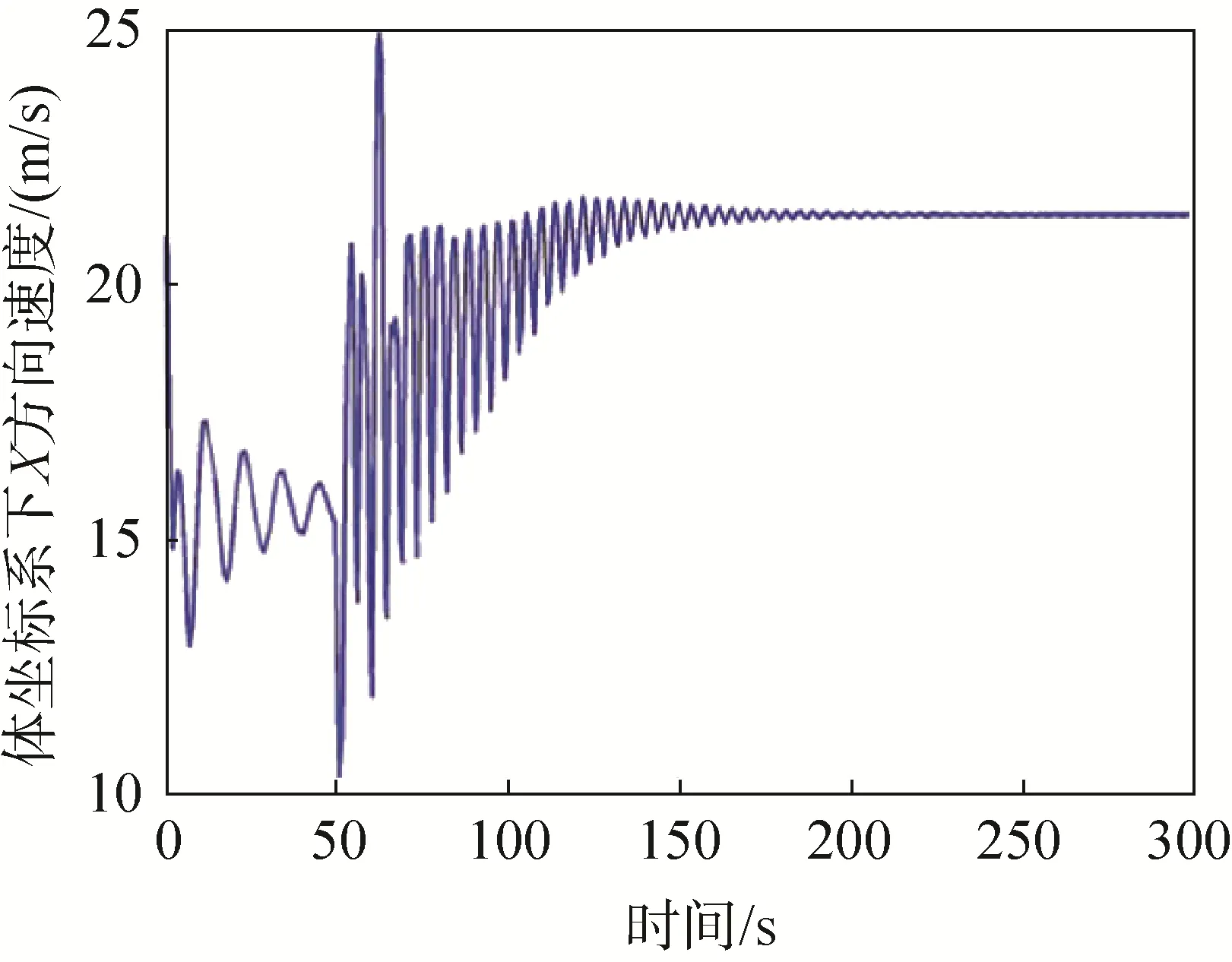
图7 X方向速度变化曲线Fig.7 X speed change
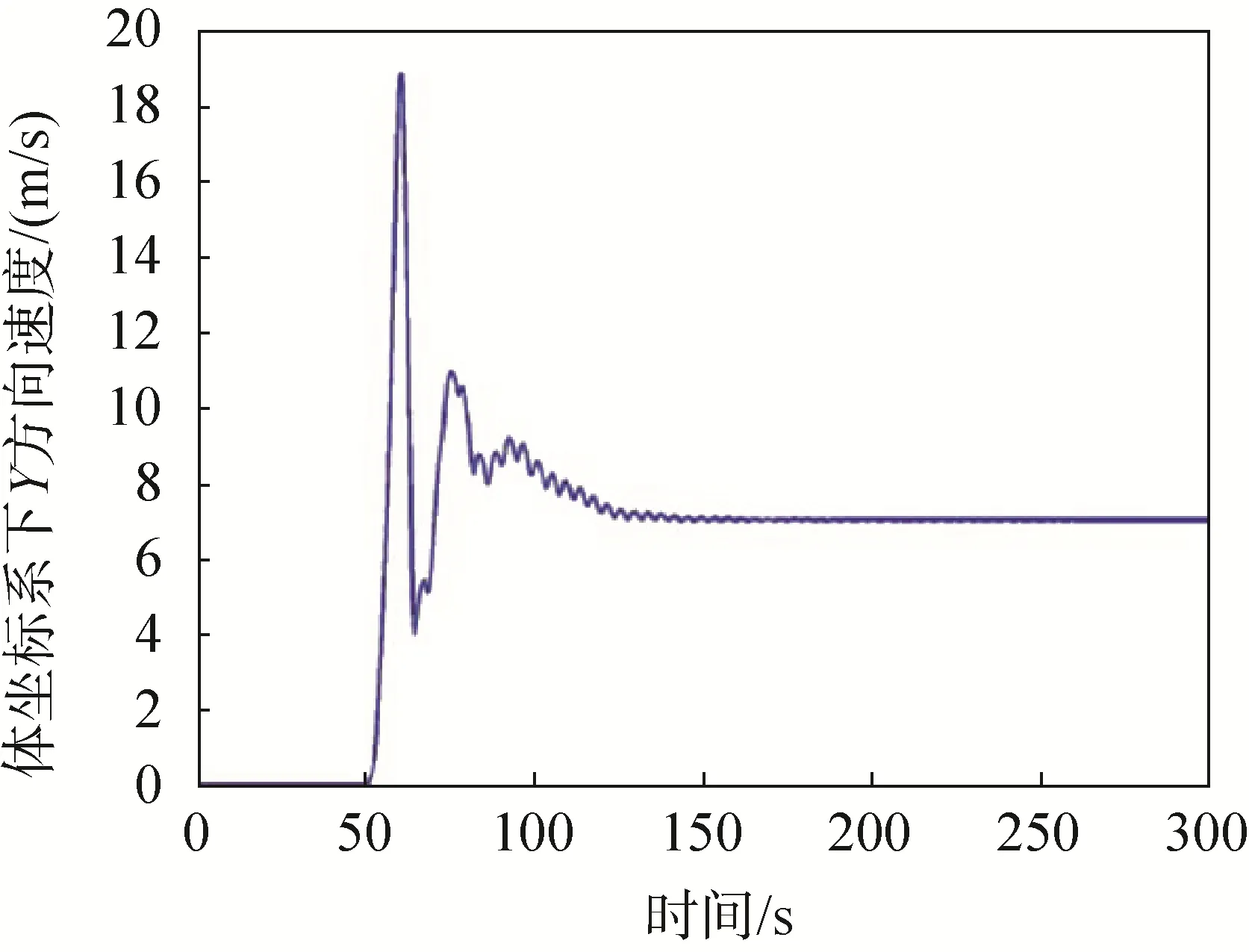
图8 Y方向速度变化曲线Fig.8 Y speed change
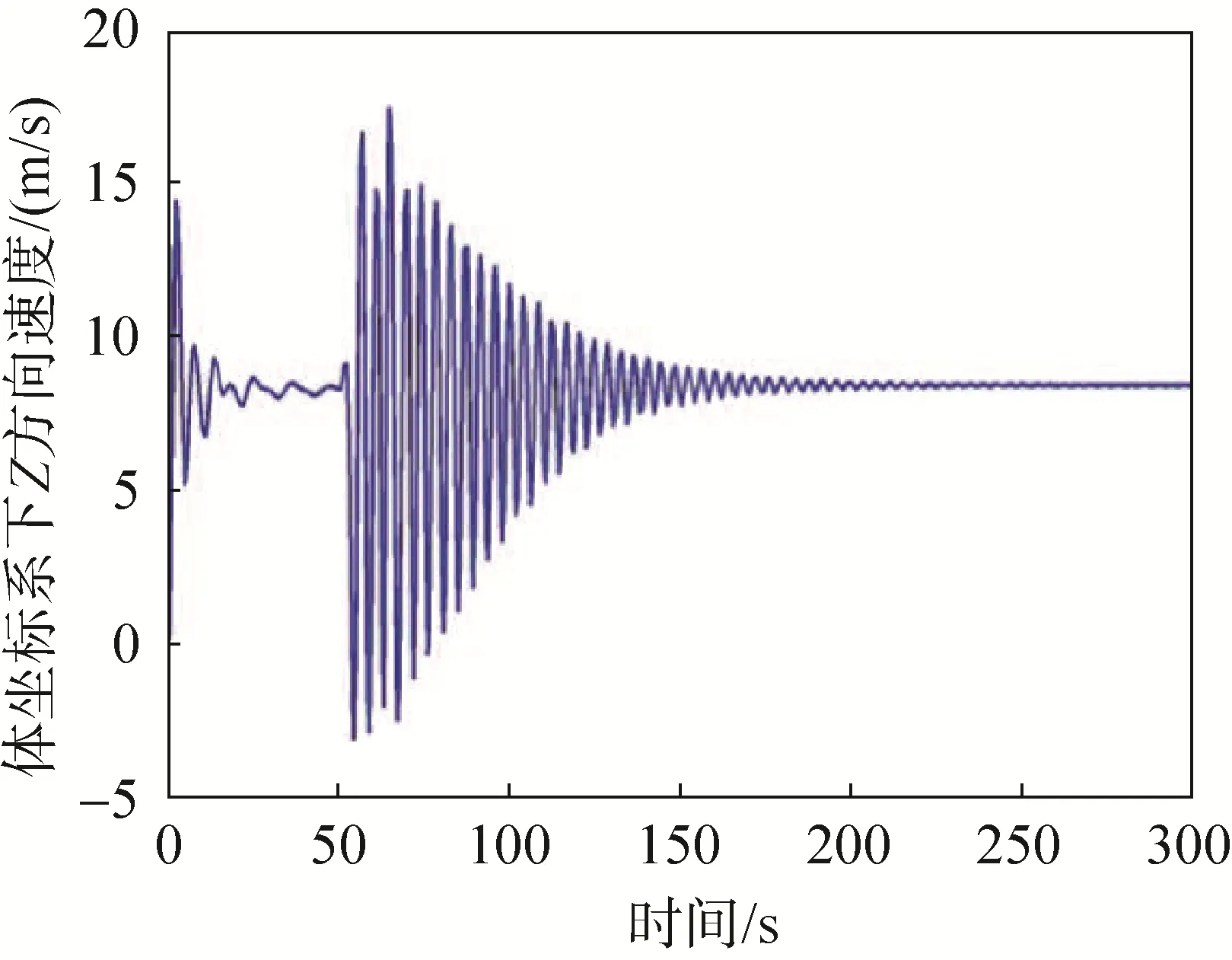
图9 Z方向速度变化曲线Fig.9 Z speed change
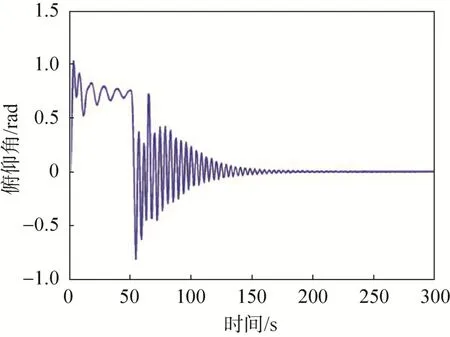
图10 俯仰角变化曲线Fig.10 Pitch angle change
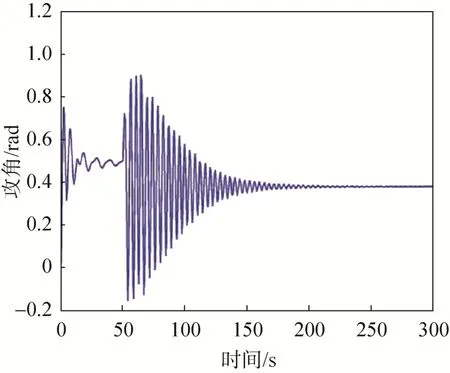
图11 攻角变化曲线Fig.11 Angle of attack change
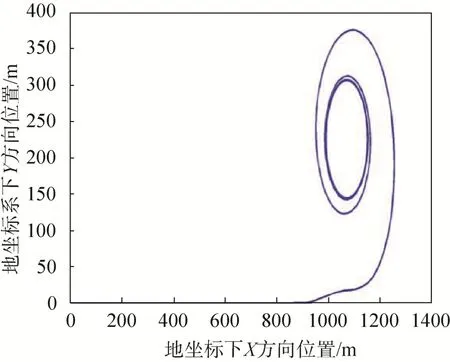
图12 水平面运动轨迹Fig.12 Horizontal plane trajectory
4.2 转弯性能分析
设定工况为0~50s滑翔运动,在50s时下拉右侧后缘操纵绳,下拉量从65%到100%,多次取值仿真,对应的不同转弯半径情况如表5所示,表中试验转弯半径中带有*的部分是由于试验数据比较离散,所以用试验条件拟合得到的数据。
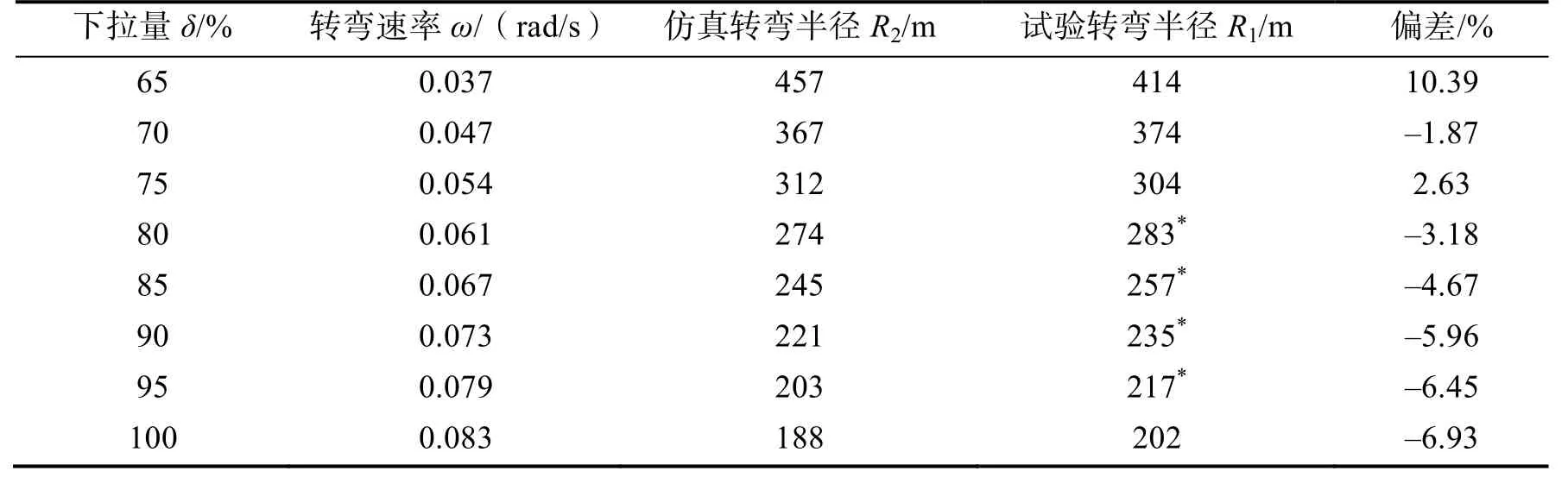
表5 下拉量与转弯速率、转弯半径间的关系Tab.5 The relationship between unilateral deflection and turning speed and radius
由表5可知,在下拉量处于70%~95%时,转弯速率与下拉量近似呈现线性变化关系。转弯半径会随着下拉量的增加而逐渐减小,且减小幅度逐渐变小。将仿真转弯半径与试验转弯半径相比较,偏差在(–6.93,10.39)之间,拟合程度较高,能反映出模型与实际运动吻合度较好。
5 结束语
一直以来,针对大型翼伞的研究都较为缺乏,多数研究也只停留在计算和仿真层面,较少有与试验数据的对比结果。本文从大型翼伞伞衣变形过程出发,分析了大型翼伞转弯过程的运动原理,通过理论推导、CFD仿真、空投试验三种方法得到了大型翼伞的侧力系数与下拉量之间的关系,经相互比较验证了推导过程的准确性,并将所得到的侧力系数公式代入动力学模型当中进行了运动仿真,得到了较为完整全面的转弯过程数据,与试验数据对比吻合较好,验证了模型的正确性,可以为大型翼伞的设计研究提供参考。

